基于OpenCL的自动微分并行实现及其应用

(1.浙江东方职业技术学院 电气自动化研究室，浙江 温州 325035；2.温州大学 电气数字化设计技术国家地方联合工程实验室，浙江 温州 325035；3.湖南大学 电气与信息工程学院，湖南 长沙 410082)

0 引言

在很多的数值优化[1]方法中都会涉及到对函数导数，雅可比矩阵的计算。在传统上，这些计算都是通过手工完成的。手工的计算方式对于很多小型的问题来说是比较简单可行的。但是对于有众多参数的复杂函数来说，手工计算其导数将是一个庞杂且容易出错的过程。随着现代计算机的迅速发展，对导数的计算都转而采用计算机来实现。当前有三种通过计算机计算导数的方式。第一种为使用有限差分近似的数值微分方式。该方式简单实用，但存在着较大的舍入和截取误差。第二种方式为是使用符号计算的符号微分，该方式可以得到精确的封闭形式的求导结果。但存在一个严重的问题，那就是随着函数的复杂度的增加，符号微分产生的符号表达式会呈指数级的增长。这就是所谓的表示式膨胀问题。而第三种方式则是本文所讨论的自动微分[5-6]方式。自动微分克服了前两种方式的缺点，会是数值计算方面主要的导数计算方式。

自动微分可以很有效地应用于计算机视觉中的大规模光束平差[2-3](Bundle Adjustment, BA)优化问题中。光束平差通过不断地优化2D点的误差来优化三维重建中相机和3D点的位置。采用的方法通常有Levenberg-Marquardt (LM)、Dog-Leg(DL)等[4]。这些方法都需要计算投影函数x=f(X)的导数来形成雅可比矩阵，其中x为2D点，X为其对应的3D点。由于3D点的数量众多，可达到上百万级。因此，对这一过程进行自动微分的并行化计算可以大大提高计算的速度。

自动微分有前向模式和反向模式两种。对于含有多个参数的函数，从 计算效率上来说更倾向于采用后向计算模式。目前存在这些通用的用于计算自动微分的软件，如ADOL-C[7]、CPPAD以及Ceres Solver。对于用于光束平差的Ceres Solver，其实现了一个基于OpenMP的自动微分。在本文中，则基于开放的OpenCL构架，提供了一个更高效的并行化自动微分实现。

1 自动微分的原理

相对于封闭形式求导结果或者近似的数值求导结果，自动微分可以获得无截断误差的数值结果。这很大程度上得益于链式法则和计算机编程模式的相结合。每一个函数可以被分解为基本运算符的组合，其中基本运算符包括加、减、乘、除等二元算术运算符，以及像三角函数和指数函数等在内的超越函数。因此函数可以采用计算图的形式来表示。例如考虑如下的函数：

(1)

式中，可以视为一个向量函数f:R2|→R2。其分解得到的计算图见0。图中每个运算都由一个带编号的节点表示。可以通过前向和反向两个模式来计算f关于x的导数。

图1 公式(1)的计算流程图

1.1 前向计算模式

令vi-n=xi,i∈[1,n]为输入，vi,i∈[1,l]为中间变量，ym-i,i∈[m-1,0]为函数fk,k=m-i的输出。一个三阶段的记法可以用来对导数的前向计算进行形式化，自动微分前向计算模式的计算过程如下所示：

(2)

(3)

(4)

式中，关系ji表示vi与vj是直接相关的。在计算图也表示节点vi是vj的一个直接后继。φi是描述基本运算的函数。ui=(vj)ji表示vi的所有前驱的集合。令所有输入为一个向量x=[x1,…xi,…,xn]。若将输入的导数设定为则就为希望计算得到的导数∂fk/∂xi。前向计算模式比较简洁易懂，并且对于f:R|→Rm这样的标量函数来说，其计算是非常有效的。因为输入参数只有一个，那么只需要令便可以计算出所有的导数值。但是对于像f:Rn|→R或f:Rn|→Rm这样的向量函数，双述的计算过程必须运行n次或n×m次。而反向的计算模式则可以避免这个问题，提高计算的效率。

1.2 反向计算模式

表1 自动微分反向计算模式的计算过程

该计算过程分为两部分。第一部分像正向计算模式一样计算出函数值。第二部分则反向地估计函数对所有输入参数的导数。对于函数f:Rn|→Rm，所示的计算过程只需要运行m次便可以获得所有的求导结果，从而得到最终的雅克布矩阵。

2 并行实现

本节中实现的基于OpenCL[8-9]的自动微分采用反向计算模式，可以用于“large-small”问题。所谓的“large-small”问题，就是单一函数的计算图并不复杂，但是却存在着大量的重复的计算。光束平差问题便是一个例子。由于大量的3D点和相机的存在，就需要计算大量的投影函数对3D点坐标和相机参数的导数，来形成最终的稀疏雅克布矩阵。基于OpenCL的自动微分的实现分为主机端和设备端两部分。在主机端运用了C++的函数重载和模板特性[10]来有效地生成计算图。而设备端则根据计算图并行地计算出求导结果。

2.1 主机端编程

为了简化使用的方式，对待求导函数的构建应该尽量的趋近于原生的C/C++风格的代码编写。式的函数可以写成如下的简洁形式：

DVAR x1,x2;

DVAR f1=ln(x1)+x1*x2-sin(x1)

DVAR f2=x1*x2

要实现如此的函数构建的简单化，需要完成一些关键的任务。首先，定义一个用于描述节点的结构体：

template

struct ADV_Node {

OpType op;

shared_ptr> arg[2];

T val;

T dval;

int id;

}

在该结构体中，OpType是一个用于指示运算符的枚举类型，指示该节点为其前驱进行某种运算的结果。除了常规的运算之外，还引入“CONST”和“INPUT”来分别表示该节点是否为常量或者函数的输入参数。每个节点在生成时还被赋予一个唯一的id值。arg指向该节点的一个或两个前驱节点，指示该节点运算符的操作数。dval用于在求导过程中存放函数对该节点的导数值。

然后，实现了一个Wrapper类ADV来描述最终的数学形式上的变量，并用此来完成数学表达式的构建。ADV类的定义如下：

template

class ADV {

public:

shared_ptr> ADVptr;

ADV();

ADV(shared_ptr> ptr);

ADV(const ADV &adv);

ADV(const T val);

ADV& operator=(const ADV &rhs);

ADV& operator=(const T &val);

}

采用智能指针来为每个ADV变量创建节点可以使得ADV变量能够不受作用域的限制，像数学形式上的函数那样完成代码中的对应函数。例如要实现一个3元素向量的点积，可以写为“dot3(ADV *a, ADV*b)”。该函数能返回一个新建的ADV变量来记录所有的运行结构。ADV类中所有的构造函数和赋值运算符重载都用来确保变量的正确生成。所有的关于ADV变量间的运算都用过类定义外的友元的函数重载来实现。每个函数重载创建新ADV变量来记录这一关于其前驱的运算。例如加法的函数重载实现为：

ADV operator+(const ADV &x,

const ADV &y)

{

ADV adv;

adv()->val=y()->val+x()->val;

adv()->op=ADD;

adv()->var[0]=x.ADVptr;

加大依法治林力度，提升森林资源管护水平，全市将以执行《烟台市森林防火条例》为总抓手，突出抓好以防火道路网、引水上山水网、预警监测网、森林消防专业队伍、专职护林队伍为主体的“三网两队”建设，大力构建森林火灾应急处置信息化、扑救队伍专业化、设施装备现代化体系，开展严厉打击非法野外用火行为专项行动，全面提升森林防火能力和法制化水平，确保全市森林防火形势持续保持平稳。同时，认真贯彻执行相关法律法规，进一步规范涉林审核审批，持续开展严厉打击乱征滥占林地、乱砍滥伐林木等违法行为专项行动，积极运用飞防、地面喷洒药物、释放天敌生物等多种措施进行综合防治，确保林业有害生物实现持续有效控制。

adv()->var[1]=y.ADVptr;

return adv;

}

程序上的“c=a+b;”表达式便可以直接地表示数学上的c=a+b。通过使用不同运算的函数重载来构造函数，函数所对应的计算图也同时被构建出来。另外对于大多数情况下使用的双精度浮点型来说，可以将ADV定义为DVAR。

2.2 计算序列的生成

在构建函数以及对应的计算图之后，便可以据此运用反向计算模式来进行导数的计算。为了正确地计算各个节点的导数值，同时也是为了便于设备端的并行计算。需要将计算图转化为计算序列。

在反向计算模式下，计算序列又分为正向计算序列和反向计算序列，正向计算序列用于计算函数值，而反向计算序列则用于计算函数的导数值。由于每个节点的id在生成时满足后继节点的id值一定大于其前驱节点的id值。所以用于计算函数值的正向计算序列可以简单地取为各节点的升序排列。然而在确定反向计算序列时，必须考虑节点之间的依赖关系。如0所示，如果先从节点7开始处理，在处理节点2时，其所依赖的节点5的导数值还并没有被计算出来。

图2 编程模式下的计算图及正向和反向计算序列

因此，采用拓扑排序来完成反向计算序列生成。所生成的反向计算序列中各节点满足相互间的依赖关系。拓扑排序的伪代码见算法1：

算法1:用于生成反向计算序列拓扑排序

输入：计算图G=(V,E)

输出：反向计算序列L

初始化计数数值C, 用于记录各节点的入度

forvinVdo

令s,t为v的前驱节点

增加s,t在C中的入度

end for

whileL非满 do

找到具有零入度的节点v

添加到L尾部

令s,t为v的前驱节点

减少s,t在C中的入度

end while

2.3 设备端并行计算

当在主机端完成计算序列的生成之后，便可以将需计算的函数的参数传入设备端，在设备端按照计算序列计算出函数值以及函数的导数值。

在OpenCL下，多个kernel函数并行地在如CPU、GPU或者FPGA设备上运行，其每个运行的实例称为一个工作项。其并行的数量取决于设备上计算单元的数量，以及计算单元上局部存储器大小等因素。主机端需要指定全局工作项的数量，其对应到需要进行求导的函数的数量。同时也可以指定局部工作项的数量，形成工作组。每个工作组中的工作项以SIMT(Single Instruction Multiple Thread)的模式，并且共享一组数量有限的高速局部存储器。在像光束平差的应用中，所有的导数计算使用相同的计算图和序列。如果计算图的尺寸比较小，那么可以将生成的计算序列传输到局部存储器以访问提高速度。

用于执行每个实际求导过程的kernel函数相对比较简单。首先按照给定的正向计算序列和函数参数值计算出函数值。然后再按照反向计算序列依次计算每个节点的导数值。最后将作为输入节点的导数返回给主机端。该计算过程的伪代码见算法2：

算法2:计算导数的Kernel函数for i=0 to size(forward_seq) do

compute_val(node_op,arg1_val,arg2_val)

end for

for i=0 to size(input_args) do

val_out[base+i]=node_val[i]

end for

for i=0 to size(funcs) do

for j=0 to size(reverse_seq)

compute_diff(node_op,node_val,

arg1_diff,arg2_diff)

end for

for j=0 to size(input_args) do

diff_out[base+i*N+j]=node_diff[j]

end for

end for

3 应用实例

四元数可以表示为q=。在相机坐标系下对3D点的旋转可以表示为：

Rot(X)=q·q(X)=q⊕q(X)⊕q-1

(5)

其中:⊕为Hamilton积，q(X)则用于将X变为四元数形式<0,X>。在Rodrigues参数形式中，旋转表示为绕单位向量k的旋转，旋转角度为θ。因此，X的旋转在Rodrigues参数形式下表示为：

Rot(X)=Xcosθ+(k×X)sinθ+

(1-cosθ)(k*v)k

(6)

通过将旋转与位移的结合，可以得到3D点在相机上的投影。在光束平差中，视3D点坐标X和相机矩阵[R|t]为投影x的参数。采用Rodrigues参数形式，编写如下的代码完成x相对于X和[R|t]的计算图的构建：

DVAR x,y;

DVAR theta2=dot(angle_axis, angle_axis);

DVAR theta=sqrt(theta2);

DVAR costheta=cos(theta);

DVAR sintheta=sin(theta);

DVAR theta_inverse=1.0/theta;

DVAR w[3]={ angle_axis[0]*theta_inverse,

angle_axis[1]*theta_inverse,

angle_axis[2]*theta_inverse

};

DVAR w_cross_pt[3];

cross(w,pt3D,w_cross_pt);

DVAR tmp=dot(w,pt3D)*(1.0-costheta);

DVAR tmp3D[3];

tmp3D[0]=pt3D[0]*costheta+

w_cross_pt[0]*sintheta+w[0]*tmp;

tmp3D[1]=pt3D[1]*costheta +

w_cross_pt[1]*sintheta+w[1]*tmp;

tmp3D[2]=pt3D[2]*costheta +

w_cross_pt[2]*sintheta+w[2]*tmp;

tmp3D[0]=tmp3D[0]+transl[0];

tmp3D[1]=tmp3D[1]+transl[1];

tmp3D[2]=tmp3D[2]+transl[2];

x=focal*tmp3D[0]/tmp3D[2];

y=focal*tmp3D[1]/tmp3D[2];

其对应的计算图见图3。该计算图随后被转化为计算序列，并伴随所有3D点坐标和相机参数送入设备的并行计算。计算出投影点坐标，以及投影点作为函数对3D点坐标和相机参数的导数。最终获得雅可比矩阵的每个块Aij和Bij。Aij为投影点坐标(x,y)对3D点坐标(X,Y,Z)的导数。Bij为投影点坐标对向量化的相机参数p的导数。

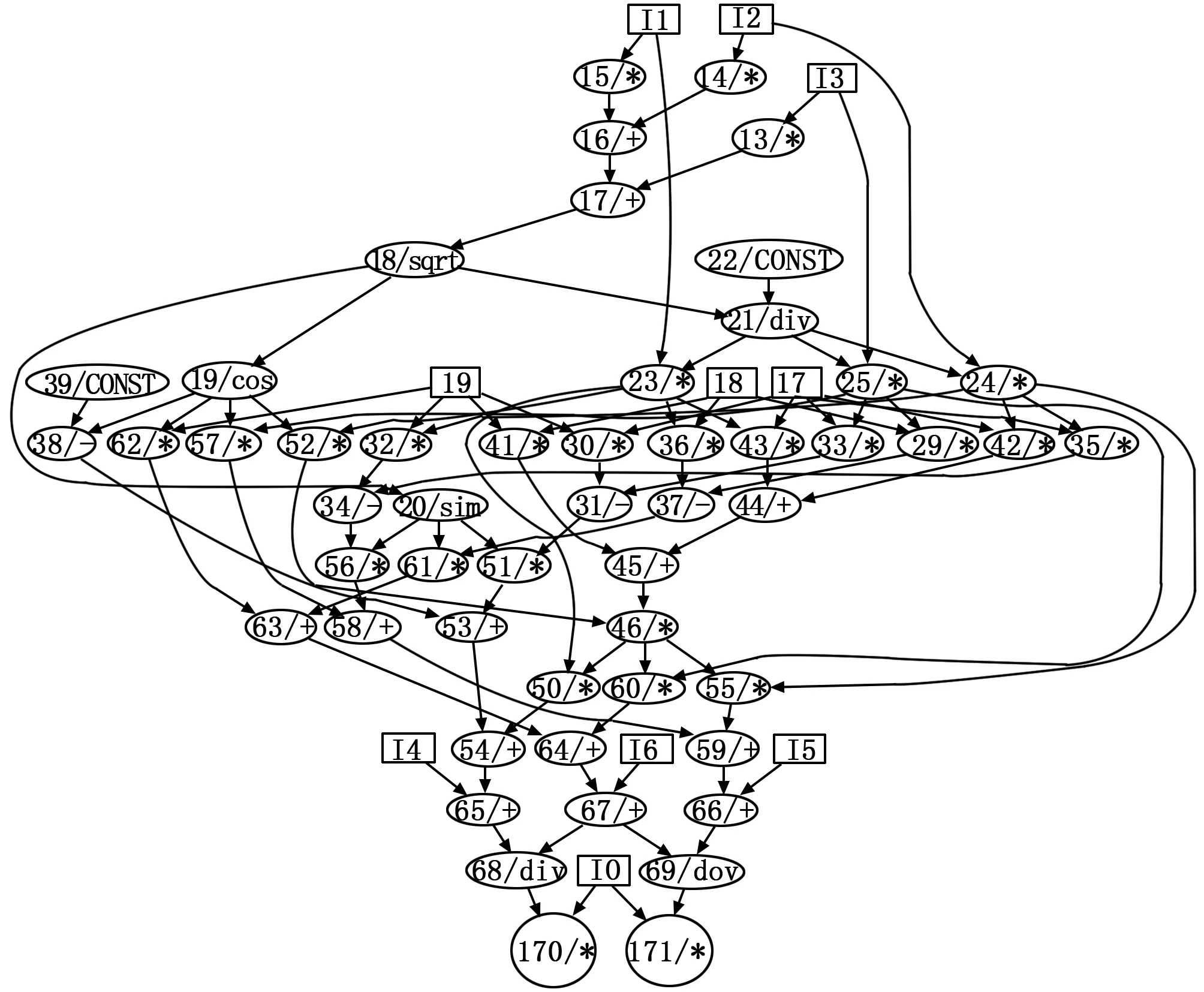
图3 Rodrigues参数形式下投影函数的计算图

4 测试与分析

本节中对实现的并行化自动微分进行测试。将其应用到BAL(Bundle Adjustment in the Large)问题[12]中。所选择的数据集见表表3。作为对比，同时引入了对Ceres Solver在该问题上的测试。Ceres Solver是Google公司推出的用于解大型数值优化问题的开源软件。其中的自动微分基于OpenMP多线程框架，在CPU上实现了线程级别的并行计算。

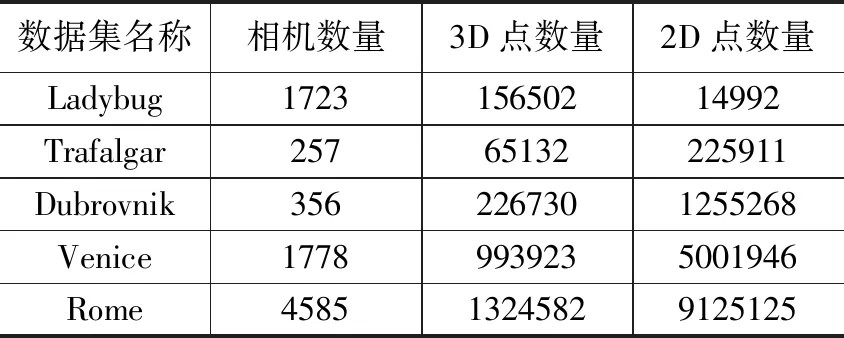
表2 各数据集的主要数据

测试的平台为一台兼容PC机。采用的处理器为Intel XEON E5 2643 v2，其共有12个超线程核心，运行频率为3.2 GHz，配备的内存为1866 MHz的8GB DDR3 RAM。 用于测试OpenCL并行计算的GPU采用AMD的R9 290，其共有40个计算单元，4GB显存，核心和显存的工作频率分别为945 MHz和1 240 MHz。R9 290能够提供很强大的并行计算能力，其单精度浮点计算性能可达4848 GFLOPS，而双精度浮点计算能力也可达到606 GFLOPS。对于大多数科学计算来说，例如使用光束平差法的优化问题，通常都使用双精度浮点数据。

图4 工作组尺寸对性能的影响

首先测试工作组的大小对计算的性能的影响，采用的数据集为Dubrovnik。工作组的大小从4变化到128。在CPU和GPU上各运行100次取均值，得到的结果见0。从结果可以看出，CPU运行所需时间普遍小于GPU所需时间。随着工作组尺寸的增长，GPU计算的性能会逐渐的下降。其主要原因在于GPU上工作组内存储器的访问冲突。GPU上的存储器按较大地址块(如1K字节)的形式访问，同一个块上的地址必须访问。而在CPU上该问题得到很大的缓解，因为CPU上的地址块大小要小很多。

在对所有的数据进行测试时，结合对工作组尺寸的分析，针对CPU采用的工作组尺寸为32，而针对GPU采用的工作组尺寸为8。所获得的测试结果见0。使用同样的CPU，本文基于OpenCL的方法比Ceres Solver基于OpenMP的方法在速度上快了大约3.6倍。而基于GPU的实现比Ceres Solver快了1.6倍。由此可见，CPU实现比GPU实现的性能要好。尽管R9 290的GPU有40个计算单元，但其只运行在1 GHz。而XEON E5的CPU运行在3.2 GHz。同时，自动微分中存在着许多的转移分支，这并不利于GPU发挥其流水线的特性。相反，CPU是被设计为执行复杂任务的，有着强大的分支预测能力。因此，大规模的自动微分更适合在多核的CPU中执行。

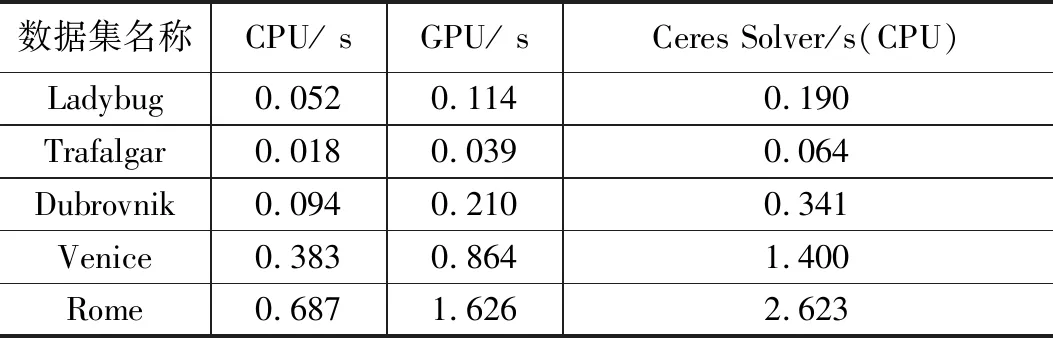
表3 自动微分在各数据集上的测试结果

5 总结

本文首先展示了自动微分系统的工作原理，包括正向模式和反向模式。对于多参数的函数，揭示了反正模式比正向模式具有更高的效率。以OpenCL为并行计算框架，实现了针对大型优化问题的并行化自动微分。该实现采用反向计算模式，以C/C++的风格构建函数，并生成计算图和计算序列。以光束平差为应用背景，通过测试，该实现比Ceres Soler快约3.6倍。同时可以发现，自动微分在CPU上的实现要优于在GPU上的实现。