小卫星对上面级定向的姿控设计与验证

(北京宇航系统工程研究所，北京 100076)

0 引言

上面级能够进一步将有效载荷从准地球轨道或地球轨道送入预定工作轨道或预定空间位置的具有自主独立性的飞行器[2]。在轨服务中一项非常重要的关键技术便是服务航天器自主逼近与捕获目标航天器的相对位置和姿态控制技术[1]。小卫星为上面级平台载荷，小卫星姿态控制系统主要任务是，通过调姿使小卫星的固定面朝向上面级平台方向，并克服展开机构展开时产生的干扰，使固定面稳定指向上面级平台。小卫星的姿态控制系统需具备速率阻尼和对上面级平台定向的功能。另外，由于小卫星在上面级平台上的安装已固定，当小卫星与上面级分离后，测控天线不朝地球方向，而且在对上面级定向后，测控天线无法朝向地球方向，这样会导致地面测控站无法收到遥测数据。所以，小卫星姿控的难点在于如何实现快速对上面级平台定向，并在对上面级平台定向完成后如何实现测控天线是朝向地球的。本文针对小卫星的这些难点，开展小卫星定姿算法、姿控算法的设计，并通过数学仿真、半实物仿真以及飞行试验对设计的姿控系统进行验证。

1 姿控系统任务分析

小卫星与上面级分离时，小卫星在分离装置内沿分离装置内的滑轨滑行2s，之后小卫星与分离装置分离，小卫星将以分离时刻的姿态角速度在空间中运动。小卫星的姿态控制系统需克服各种空间环境的干扰，使小卫星飞行器姿态稳定，并使小卫星的固定面朝向上面级平台，为上面级平台的光学跟瞄装置提供远距离跟瞄的条件。在试验过程中需将遥测数据下传，需小卫星的姿控进行调姿，使测控天线朝向地球，为建立遥测天地链路提供条件。

2 系统硬件设计

2.1 软件设计思路和编程方法

针对小卫星任务需求，小卫星的姿态控制需完成星箭分离后的速率阻尼、对上面级平台定向的功能，本系统采用连续型时变输出执行机构(飞轮控制)，利用简化的数学模型和输出反馈控制可以设计具有一定鲁棒性和优化性能的控制器以实现姿态控制[4]。小卫星分离后，首先进入无控模式，随后进行速率阻尼模式，在三轴姿态角速度小于0.1°/s或时间到达一定时间后，由速率阻尼模式转入对上面级平台定向模式，展开帆板后一直保持对上面级平台定向，直至任务结束。根据任务的功能要求，设计小卫星为零动量三轴稳定系统，使用1个三轴陀螺作为姿态敏感器、3个反作用飞轮沿小卫星本体正交安装作为姿控系统的执行结构，采用4阶龙格库塔积分算法进行定姿，速率阻尼阶段采用角速率反馈控制，对上面级平台定向阶段采用递阶饱和PD控制。

在姿控方案中使用飞轮对小卫星进行速率阻尼，通过陀螺积分定姿与递阶饱和PD控制算法，以实现小卫星对上面级平台的快速定向；在对上面级平台定向的过程中，通过绕小卫星本体x轴转动一个角度(具体数值可根据分离时刻的轨道位置确定)，可实现测控天线超向地球。下面首先描述小卫星的姿态运动学与动力学，然后分别设计定姿算法与姿控算法。

2.2 姿态运动学与动力学模型

由于小卫星本体和展开机构均为刚性结构，所以，小卫星的姿态描述可用刚体的姿态模型描述，由于小卫星姿态存在大角度姿态机动，使用欧拉角描述姿态运动可能出现奇异问题，为了避免该问题，使用姿态四元数描述小卫星的姿态运动。

定义q为小卫星本体相对于惯性空间的姿态四元数，定义ω为小卫星相对惯性空间的姿态角速度，则小卫星的姿态运动学方程可描述为：

(1)

(2)

式中，q0为姿态四元数q的标部；qv为姿态四元数的矢部；ω×为ω的反对称阵。

姿态四元数满足归一化约束，即：

q02+qvTqv= 1

(3)

将微小卫星视为刚体，动力学方程可表示为[3]：

(4)

式中，Is为小卫星的转动惯量矩阵；h为小卫星的角动量；Tc和Td分别为作用在小卫星上的控制力矩和干扰力矩。

2.3 定姿算法设计

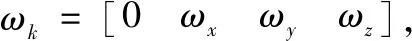
(5)

(1)计算k1：

k1=qk-1⊗ωk-1

(6)

式中，⊗表示四元数乘法。

(2)计算k2：

(7)

(3)计算k3：

(8)

(4)计算k4：

(9)

综上，可确定当前时刻的姿态四元数为：

(10)

2.4 姿控算法设计

由于小卫星与上面级平台分离后会具有一定的姿态角速度，因此，要实现小卫星对上面级平台的快速定向，首先需要将小卫星的姿态角速度快速降低，为小卫星对上面级平台定向做好准备，可通过速率阻尼的方式实现这一目标。速率阻尼完成后，需要调整小卫星的三轴姿态，将小卫星固定面快速调至对上面级平台的方向，即通过对上面级平台定向的模式来实现这一目标。

2.4.1 角速度反馈控制

采用角速度反馈控制的方式，可实现小卫星姿态角速度的快速阻尼，将小卫星的姿态角速度阻尼至较小值后，再转入对上面级平台定向模式。

角速度反馈控制律如下：

Tc=-kdampω

(11)

其中： 阻尼系数kdamp为三维正定对角阵。

2.4.2 递阶饱和PD控制算法设计

递阶饱和PD控制算法实质上是一种特殊的PID控制算法，与传统PID控制算法的不同之处是当姿态偏差较大时，在每个控制周期内只截取其中的一部分偏差进行控制，逐步消除姿态偏差，以实现小卫星逐渐逼近期望姿态的目的；当姿态偏差较小时，在每个控制周期内直接对该偏差进行控制，进而消除该偏差。

2.4.2.1 姿态指令分析

由于小卫星与上面级平台分离后，需要对上面级平台定向，所以，选取分离时刻的惯性坐标系作为姿态参考坐标系，定义分离时刻的惯性坐标系为oxdydzd，简称分惯系，以上面级分离小卫星时刻上面级体坐标系为分离惯性系，分惯系与上面级分离小卫星时刻上面级体坐标系ox1y1z1重合。

因此，小卫星要实现对上面级定向，需要将小卫星本体相对于分离惯性系的姿态四元数稳定在[1.0, 0.0, 0.0, 0.0]。考虑到小卫星在上面级平台上安装时，小卫星的本体坐标系与上面级的本体坐标系重合，小卫星与上面级分离时，上面级平台的-y轴朝向地球，要使小卫星本体的z轴(安装测控天线面)朝向地球，小卫星本体还需要绕其x轴转动约90°(需要的最大转动为90°)，为考核姿态控制系统的控制能力，所以，这里按照转动90°进行设计与验证，所以，小卫星的姿态四元数指令qc为[0.7071, 0.7071, 0.0, 0.0]，由于是对上面级平台稳定定向，所以，姿态角速度指令ωc为[0, 0, 0]。

2.4.2.2 姿态控制律设计与稳定性分析

定义姿态四元数和姿态角速度指令分别为qc和ωc，姿态四元数偏差和姿态角速度偏差分别为：

⊗q

(12)

ωe=ω-ωc

(13)

由于姿态四元数存在归一化约束，所以，只需对姿态四元数的矢部进行控制，设计姿态控制律如下：

Tc=-kpqev-kdωe+ω×h

(14)

式中，qev为姿态四元数偏差qe的矢部；kp为比例系数；kd为微分系数。

小卫星绕其3个主轴的转动惯量分别为Jx=0.6 kg·m2，Jy=1.2 kg·m2，Jz=1.12 kg·m2。结合小卫星的姿态运动学与动力学模型，设计三轴姿态控制参数。

下面通过控制系统的bode图和根轨迹图来分析控制系统的稳定性。通过使用Matlab软件，得到应用PD控制算法时的姿态控制系统的三通道bode图分别如图1、图2和图3所示，小卫星的转动惯量由原来的80%变化到120%时，姿态控制系统的三通道根轨迹图分别如图4、图5和图6所示。

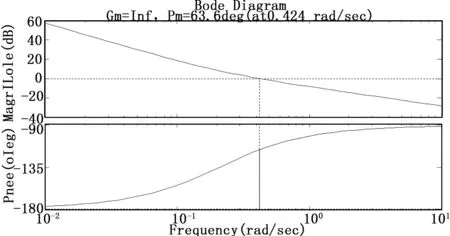
图1 滚转通道的开环bode图

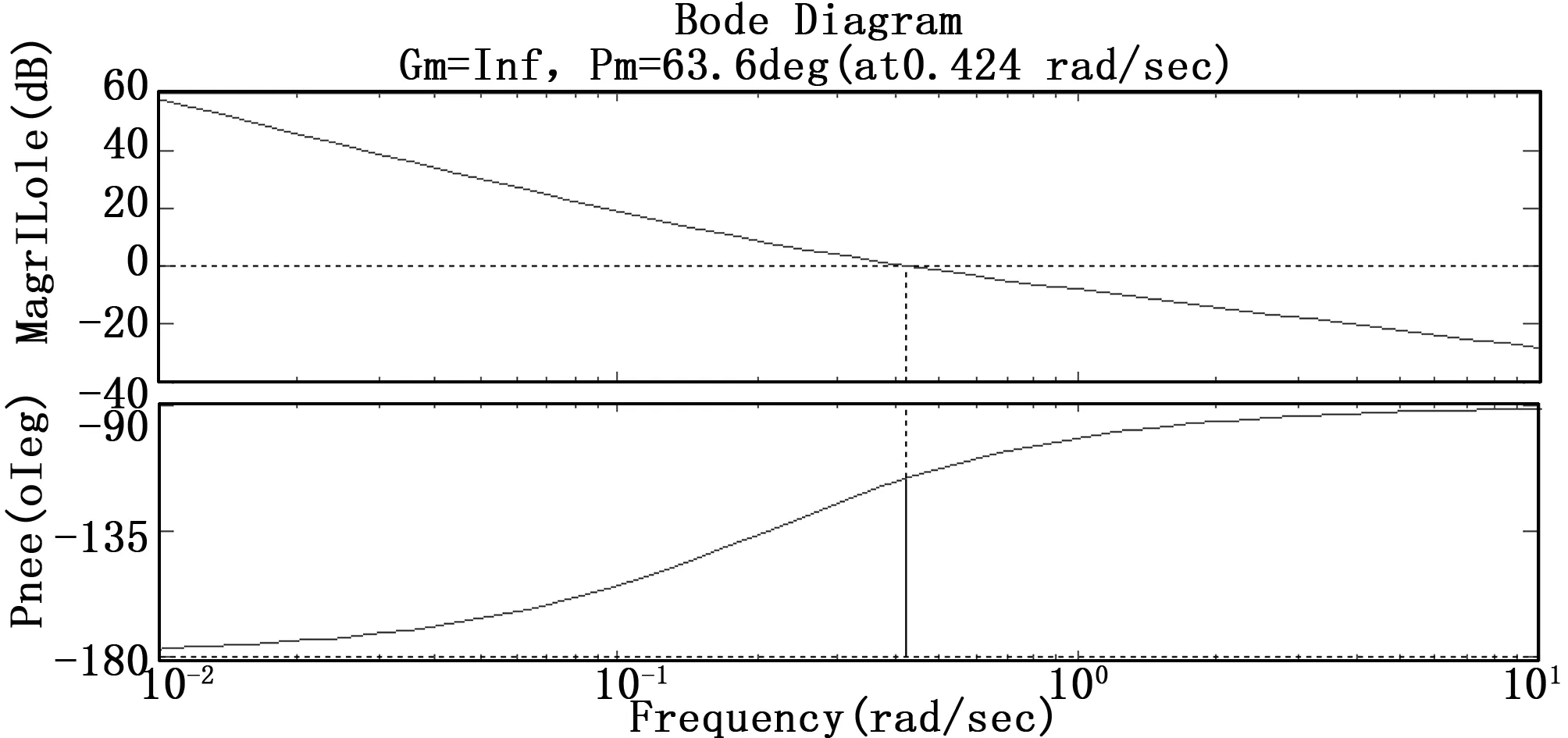
图2 俯仰通道的开环bode图

图3 偏航通道的开环bode图

图4 滚转通道的根轨迹图

图5 俯仰通道的根轨迹图

图6 偏航通道的根轨迹图

由图1、图2和图3可知，设计的滚转、俯仰和偏航三通道的幅值裕度为正无穷，相位裕度为63.6°。由图4、图5和图6可知，当小卫星的转动惯量由原来的80%变化到120%时，滚转、俯仰和偏航三通道的闭环极点都在左半平面内，并且距离虚轴有一定的距离，所以，小卫星的转动惯量变化在±20%范围以内时，上述设计的姿态控制系统是稳定的。

2.4.2.3 姿态四元数偏差限幅

对姿态四元数偏差的矢部进行限幅，具体表达式如下：

(15)

式中，ke=‖qev‖∞；qemax为姿态四元数偏差的限幅值。

2.4.3 控制力矩限幅

根据飞轮的安装，可得每个飞轮的力矩指令为：

Tcwheel=DwheelTc

(16)

式中，Tcwheel为每个飞轮的力矩指令；Dwheel为飞轮分配矩阵。

由于飞轮的最大输出力矩有限，为了保证控制系统的跟踪性能，对控制力矩进行限幅处理，使用饱和函数的方式对积分项进行限幅，具体如下：

(17)

式中，kT=‖Tcwheel‖∞；Tcmax为飞轮可提供的最大输出力矩。

2.4.4 生成转速指令

由于通过设计控制算法得到的指令为控制力矩指令，对于转速反馈式飞轮，其接收的指令是转速指令，所以，当选取转速反馈式飞轮为姿态控制的执行机构时，需要将控制力矩指令转化为转速指令，具体如下。

(1)形成角动量指令：

(18)

式中，H0为飞轮初始角动量，Ts为控制周期。

(2)形成转速指令：

(19)

式中，Jwheel为每个飞轮的转动惯量形成的对角阵。

(3)转速指令限幅：

(20)

式中，ωwheelcj为第j个飞轮的转速指令，ωwheelcmax为飞轮的最大转速，kwheel为安全系数。

3 仿真验证

为了验证上述设计的姿控方案、定姿算法、姿控算法，开展姿控系统的数学仿真与半实物仿真，具体仿真情况分别如下。

3.1 数学仿真验证

根据上述设计的定姿算法与控制算法，使用C语言编制姿控的箭上程序(算法)，并使用Matlab/Simulink搭建小卫星的姿态运动学与动力学模型、陀螺测量模型、反作用飞轮模型、轨道模型、干扰力矩模型(主要考虑气动干扰力矩、重力梯度干扰力矩、普遍的常值干扰力矩与周期性干扰力矩)，进行了多种初始状态下的数学仿真。现给出其中一种工况下的仿真结果，分离时姿态角速度为[3,-3,3]°/s，期望的姿态四元数为[0.7071, 0.7071, 0.0, 0.0]，飞轮最大角动量为0.3 N·m·s，飞轮最大转速为±6 000 rpm，仿真800 s，仿真结果如下：

图7 姿态四元数

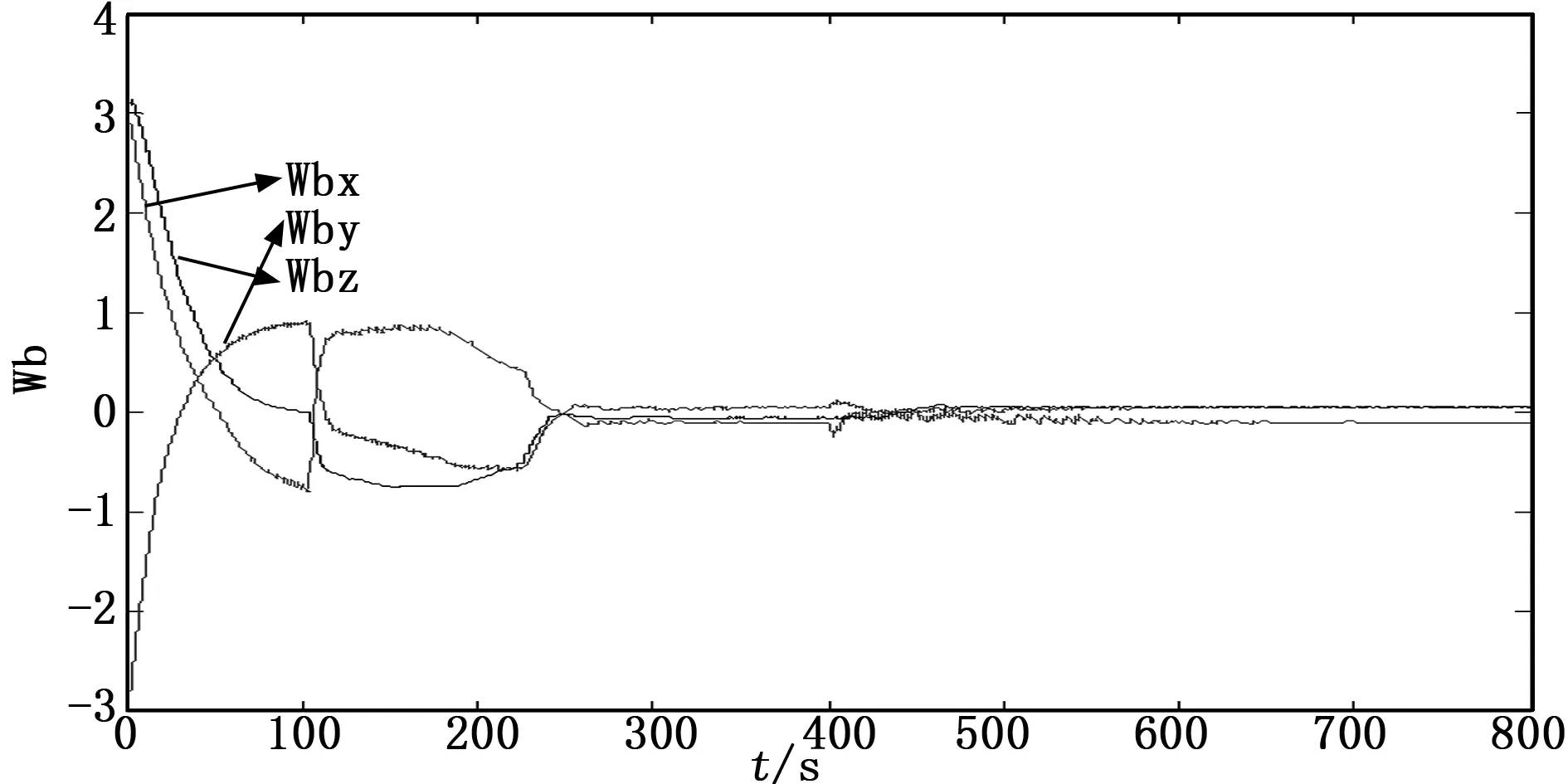
图8 姿态角速度

图9 飞轮角动量

图10 轴飞轮转速

图11 轴飞轮转速

图12 轴飞轮转速

根据上述仿真结果，小卫星本体相对于分离惯性系的姿态在240 s左右稳定，实现了对上面级平台的定向。三轴飞轮的角动量最大不超过0.17 N·m·s，有一定余量，三轴飞轮的实际转速也都跟踪上了指令转速。

3.2 半实物仿真验证

在数学仿真的基础上，搭建小卫星姿控系统的半实物仿真平台，并开发相应的软件。使用C语言编制任务管理软件，通过任务管理软件调用姿控程序，使用任务管理组合、实时仿真机、供配电单元、反作用飞轮等实物开展姿控系统半实物仿真。供配电单元为任务管理组合与飞轮供电，任务管理组合上运行任务管理软件与姿控软件，实时仿真机上运行小卫星姿态模型、陀螺测量模型和轨道模型、干扰力矩模型，半实物仿真示意图如图13所示。

图13 小卫星姿控系统半实物仿真示意图

小卫星姿控系统半实物仿真平台搭建完成，相关软件完成开发调试后，开展小卫星姿控系统的半实物仿真，主要进行了两类半实物仿真，一类是飞轮开环跟踪的姿控系统半实物仿真(主要验证飞轮的动态跟踪性能)，另一类是飞轮闭环跟踪的姿控系统半实物仿真(主要验证姿控系统功能与性能、重点验证姿控算法)。飞轮开环跟踪为姿控系统使用飞轮模型进行闭环控制，飞轮接收转速指令进行转速跟踪，但飞轮实际转速不接入姿控回路。飞轮闭环跟踪为飞轮实物接入姿控回路，飞轮接收转速指令进行转速跟踪，同时将飞轮的实际转速接入姿控回路，并根据飞轮实际转速生产控制力矩，作用在小卫星的姿态动力学模型上。分别对这两类情况进行了大量的半实物仿真，选取与上述数学仿真初始状态同样的仿真情况。

由飞轮开环跟踪的姿控系统半实物仿真结果可知，小卫星姿态稳定，距离分离时刻240 s左右实现了对上面级平台的定向，3个飞轮的转速跟踪正常。由飞轮闭环跟踪的姿控系统半实物仿真结果可知，小卫星与上面级平台分离后实现了姿态稳定，并在距离分离时刻240 s左右实现了对上面级平台的定向，验证了姿控算法的正确性，3个飞轮的转速跟踪正常。飞轮闭环跟踪曲线与飞轮开环跟踪曲线趋势一致，在时间转速上略有差别。最后对实际飞行试验结果分析，姿控系统设计正确，满足技术要求。

4 结论

本文研究了小卫星对上面级定向的姿控系统，设计了小卫星对上面级定向的姿控方案，针对小卫星对对上面级快速定向与对地数传的问题，设计了基于陀螺的4阶龙格库塔积分算法与递阶饱和PD控制算法，并通过数学仿真对设计的姿控方案、姿控算法进行了初步验证。在此基础上，搭建了小卫星姿控系统半实物仿真平台，进行了飞轮闭环跟踪的小卫星姿控系统半实物仿真，进一步验证了姿控方案、姿控算法设计的正确性。最后经过飞行试验，对实际飞行结果分析，证明了姿控系统设计的正确性。