全球视野的大类资产风险溢出研究

陈声利，赵学军，张自力

1 北京大学 光华管理学院，北京 100871

2 嘉实基金管理有限公司，北京 100005

引言

随着金融国际化程度不断加深，国家或地区之间的金融活动相互渗透，金融风险跨市场、跨区域、跨品种的传染不断加剧。金融市场间不仅存在资产价格方面的相互影响，还普遍存在资产波动率方面的相互影响。一个金融市场的波动可能引起另一个金融市场的波动，这种现象称之为波动溢出效应。由于波动率测量了市场风险，波动溢出又被称为风险溢出。近年来，全球金融市场经历了多次严重的金融危机，如亚洲金融危机、美国次贷危机等。金融风险往往从一个市场产生，然后传导到另一个市场，在风险传播过程中经常出现波动加剧、多市场共振的现象。准确测量金融市场的风险溢出效应，不仅有助于深入理解金融风险传播机制，还有助于监管部门制定政策、投资者管理风险和投资决策。

当前，全球经济形势很严峻，各国利率政策、中美贸易摩擦、英国脱欧以及地缘冲突等不确定性，将对全球金融市场产生持续性冲击。作为流动性最强的外汇市场往往与股票市场和大宗商品市场有千丝万缕的联系，从全球视野研究汇率、股市、大宗商品波动的相互溢出，有助于追溯风险源，对大类资产配置具有重要意义。本研究基于修正的已实现波动率建立向量自回归模型，利用广义误差方差分解方法构建方向性风险溢出指数和风险溢出网络，通过静态分析和滚动分析研究全球27种资产的风险溢出行为。

1相关研究评述

1.1研究方法

风险溢出一直是研究热点，针对风险溢出的研究方法也不断创新。学者们早期使用GARCH模型建模研究风险溢出。HAMAO et al.[1]利用GARCH建立两步法，先用GARCH对资产建模并提取残差，然后将残差平方作为资产波动率放入其他资产的GARCH模型中，通过估计系数的显著性判断是否存在风险溢出效应；CHEUNG et al.[2]提出基于GARCH模型标准化残差的交叉相关函数的风险溢出检验方法；李成等[3]和BILLIO et al.[4]使用多元GARCH和多元SV等多元波动率模型，从方差因果性检验视角研究风险溢出问题。此外，也有学者通过分析因子模型的结构变化考察是否存在金融传染[5-7]。当研究的资产较多时，上述研究方法估计参数比较难。

从脉冲分析视角研究风险溢出是比较常用的方法。考虑多变量的非线性建模，KOOP et al.[8]建立非线性模型的脉冲分析方法。考虑多变量的线性建模，许多学者建立VAR模型的脉冲分析方法。PESARAN et al.[9]针对非严格VAR模型或协整VAR模型建立广义脉冲分析方法；SOYDEMIR[10]基于平方收益率、已实现波动率、极差波动率等波动率代理变量构建VAR模型，通过VAR模型及其脉冲响应分析研究风险溢出关系；DIEBOLD et al.[11]基于VAR模型的方差分解进一步构建风险溢出指数，并计算不同市场的净溢入指数和净溢出指数。以上研究方法一般从全样本视角研究资产之间的溢出效应，但无法研究风险溢出效应的时变特征，也无法得到所有资产的净风险溢入、净风险溢出和整体溢出效应。

随着经济形势和市场结构的变化，金融资产之间的风险溢出效应也会动态变化，针对时变的风险溢出行为研究一般采用滚动时间窗VAR方法。DIEBOLD et al.[11-13]利用滚动时间窗VAR建模和方差分解，实现对风险溢出效应的时变估计，构建总溢出指数和方向性溢出指数，探讨不同资产之间的时变净溢入和净溢出效应(简称为DY模型)；DEMIRER et al.[14]通过结合LASSO估计将DY模型扩展到越来越相关的高维环境。由于Diebold-Yilmaz框架可以用资产的已实现波动率作为变量进行VAR建模[15]，随着已实现半方差的提出[16]，BARUNK et al.[17-18]和APERGIS et al.[19]基于好坏波动率建立了不对称波动率的溢出研究方法。

随着资产数量增多，仅用计量方法很难直观分析风险溢出效应，近年来复杂网络或知识图谱为金融资产风险溢出研究提供了新工具。如果将金融资产视为复杂网络的节点，将资产之间的风险传导关系视为复杂网络的边，那么可将金融资产构建为风险溢出网络。代表性成果是DIEBOLD et al.[13]在DY模型基础上建立有向网络，并用网络拓扑方法研究金融危机期间的风险溢出。进而，DIEBOLD et al.[20-21]利用有向溢出指数和风险溢出网络研究金融机构、金融市场和宏观经济的风险溢出效应。

1.2实证研究

实证研究风险溢出一直很活跃，学者们研究不同股市之间的风险溢出效应。HAMAO et al.[1]建立GARCH模型研究风险溢出，发现美国、英国和日本股市之间存在风险溢出关系；BARUNK et al.[17]利用好坏波动率建立VAR模型，研究发现美国股市存在不对称溢出效应。关于A股的风险溢出的研究，裴茜等[7]研究发现中国股票行业指数之间存在风险传染，而郑挺国等[22]研究发现股市风险溢出效应与政策不确定性有一定关联。为探讨A股与海外市场的联动性，张兵等[23]、李红权等[24]和周璞等[25]研究发现A股与美股、港股之间存在较强的风险溢出效应。这些研究对风险溢出效应都展开了静态分析和滚动分析。

外汇市场受国际形势影响很大，使关于汇率风险的研究备受重视[26]。关于人民币汇率的溢出行为，赵华[27]研究发现人民币汇率与利率之间存在风险溢出效应，陈云等[28]研究发现人民币汇率对股票市场具有风险溢出效应，郝毅等[29]利用MVMQ-CAViaR模型研究发现境内外人民币外汇市场存在风险溢出效应。不同汇率市场的风险溢出也是研究重点。GREENWOOD-NIMMO et al.[30]利用DY模型研究发现10种汇率存在风险溢出效应；BARUNK et al.[18]基于好坏波动建立VAR模型，研究发现外汇市场出现不对称溢出效应。这些成果为汇率风险的传染机制提供了经验证据。

随着跨市场风险的不断增加，跨市场风险溢出也是实证研究的焦点。一些学者研究商品期货与股市的联动性，王鹏等[31]研究发现石油期货与股票市场存在风险溢出效应。也有学者研究地域性风险传染，华仁海等[32]研究发现国内外期货市场之间存在风险溢出效应。部分学者研究汇市、股市和债市的联动性，陈创练等[33]改进VAR模型和脉冲分析，研究发现外汇市场、债券市场和股票市场存在交叉溢出关系；周爱民等[34]利用GARCH建模研究发现股票市场与外汇市场之间存在风险溢出效应。此外，还有学者聚焦于中美利率政策的溢出效应，郭栋[35]基于GVAR和TVP-VAR模型研究发现美国国债利率对中国债市存在冲击行为。这些研究充分表明，外汇市场、股票市场和大宗商品市场存在较强的风险传染。

随着资产数量增多，学者们采用DY模型的滚窗方法研究风险溢出行为。部分学者聚焦在贵金属市场的风险溢出研究，LUCEY et al.[36]建立DY模型研究发现伦敦、纽约、东京和上海4个黄金市场之间的风险溢出，BATTEN et al.[37]研究发现黄金、白银、铂金和钯金4种贵金属之间的风险溢出效应。诸多学者把焦点放在全球股市之间的风险传染，梁琪等[38]基于有向溢出指数研究发现中国股市与海外股市存在风险传染行为，YAROVAYA et al.[39]研究发现欧洲、亚洲等4个区域21个股市之间存在风险溢出效应。有些学者从恐慌指数视角研究风险传染，YANG et al.[40]根据11个金融市场的恐慌指数(VIX)研究发现，美国量化宽松政策对国际主要市场具有风险溢出效应。此外，还有学者同时研究股市、债市和期市的交叉溢出效应，刘超等[41]研究发现中国股市、债市、商品等市场之间存在风险溢出效应。由此可知，已有研究采用不同数据验证了DY风险溢出研究方法的有效性。

1.3研究不足和对策

根据上述分析可知，在资产数量较多的情况下，DY框架已成为研究大类资产风险溢出的主流方法。DY框架衍生出的方向性溢出指数和风险溢出网络为研究风险溢出提供了有效工具，人们既可以使用时变溢出指数研究风险溢出的动态演变，又能进一步转化为风险溢出网络直观揭示金融资产之间的风险传染机制。然而，已有实证研究依然存在不足：①学者们局限于研究两个市场内的风险溢出关系，鲜有学者将全球金融市场视为一个整体研究风险溢出效应；②外汇市场、股票市场和期货市场之间的相互溢出研究成果很少；③较少学者从大类资产视角研究每个资产的风险溢出表现；④复杂网络是研究风险溢出效应的新方法，然而除DIEBOLD et al.[13,20-21]发表的成果外，其他学者的研究贡献十分有限。

为了弥补以上不足，本研究沿用DY框架构建时变风险溢出指数和风险溢出网络，从全球视角对外汇市场、股票市场和期货市场的27种资产展开详实的风险溢出行为研究。既考察同类资产的风险传染机制，又探讨交叉市场的风险联动，可为大类资产的风险溢出提供较为全面的经验证据。

2理论方法

2.1波动率的测量方法

首先阐述风险溢出测量方法中所采用的已实现波动率。令prit为t时刻的资产价格，则对数化的价格为ρt，ρt=log(prit)，可以表示为连续时间过程，即

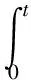
(1)

其中，μη为局部有界的均值变量，σs为数值为正的随机波动变量，η和s为时间变量，Jt为跳跃成分。对数价格ρt的二次变差过程为

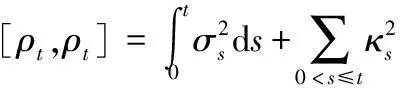
(2)

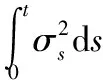
为了估计二次变差，ANDERSEN et al.[15]首次提出已实现波动率，并证明在无市场微观结构噪声条件下，它是二次变差的一致估计量。假设rk为高频对数收益率，则定义已实现波动率为

(3)

其中，RV为已实现波动率，n为抽样频数，k为循环变量。当n趋于无穷时，RV的概率收敛于二次变差[ρt,ρt]。

考虑到市场微观结构噪声的影响，本研究采用HANSEN et al.[42]提出的已实现核估计对已实现波动率进行噪声纠偏。根据陈声利等[43-44]的推导，将(3)式修正为

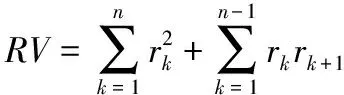
(4)

2.2风险溢出的建模理论

溢出指数计量方法最早由DIEBOLD et al.[11]提出，该方法基于向量自回归模型刻画多变量之间的线性关系，通过预测误差方差分解得到广义误差方差分解矩阵，用来描述变量之间的相互关系。在此基础上，DIEBOLD et al.[11-12]提出总溢出指数、有向溢出指数和净溢出指数。下面将系统阐述风险溢出的相关理论。

2.2.1 VAR模型和方差分解

若研究金融市场的N个资产之间的风险溢出行为，可以将N个资产的已实现波动率向量作为回归变量，建立p阶的向量自回归模型(VAR(p))，表示为

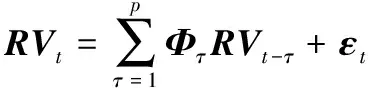
(5)

其中，RVt为已实现波动率向量，RVt=(RV1t,RV2t,…,RVNt)′；Φτ为N×N维的系数矩阵；τ为阶数的循环变量；εt为N×1维的随机扰动项，且εt～iid(0,Σε)，Σε为N×N维的εt的协方差矩阵。VAR(p)的移动平均形式为

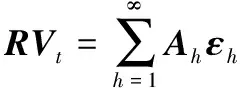
(6)

其中，h为循环变量；Ah为系数矩阵。当h<0时，Ah=0；当h>0时，Ah满足递归过程，即

Ah=Φ1Ah-1+Φ2Ah-2+…+ΦpAh-p

(7)

特别的，A0为N×N维的单位矩阵。据此，考虑向前H步预测，可计算出H个系数矩阵，即A0,A1,…,AH-1。

令i和j代表两个不同的资产，则预测误差方差分解的核心任务是，估计i资产向前H步预测的误差方差中有多少成分来自于j资产的新息冲击。在VAR(p)模型一般框架下，根据PESARAN et al.[9]的广义脉冲函数可计算出N×N维广义误差方差分解矩阵Θ，矩阵中的每个元素为

(8)

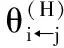
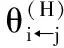
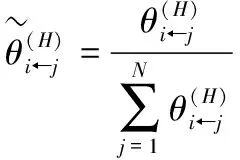
(9)

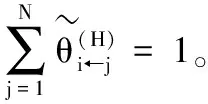
2.2.2 风险溢出的测量方法

(1)总风险溢出指数，测量N个资产波动率之间的相互溢出效果对总预测误差方差的贡献，计算方法为广义误差方差分解矩阵的所有非对角元素求和取平均，即

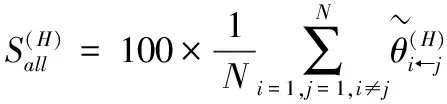
(10)

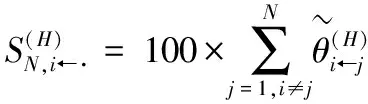
(11)

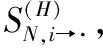
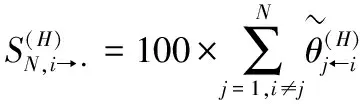
(12)

(11)式和(12)式计算得到的皆为方向性的溢出指数，后文分别将二者简称为溢入指数和溢出指数。

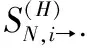
(13)

2.3风险溢出网络

多种金融资产之间的风险传染是通过波动率的相互溢出实现的，因此可以使用复杂网络方法建立金融风险溢出网络。基于复杂网络构建风险溢出网络的核心思想是，将金融市场中各类金融资产作为节点，节点之间的连边代表资产之间的风险溢出关系。借鉴DIEBOLD et al.[13,20]的研究，本研究将广义误差方差分解矩阵作为金融风险溢出网络的连接矩阵，构建面向大类资产的风险溢出网络，并通过节点的网络中心度分析大类资产之间的风险传染机制。

根据复杂网络的定义，节点的网络中心度为该节点相连的边的权重之和，用以衡量节点的重要性。节点的网络中心度越大，该节点在金融风险溢出网络中所处的地位越重要。对于有向网络而言，网络中心度又分为出度和入度。由于广义误差方差分解矩阵是有方向的，本研究构建的金融风险溢出网络本质上是有向网络。前文建立的有向溢出指数，即溢出指数和溢入指数，可以直接体现为节点的加权出度和加权入度。在具体的实证研究中，本研究在构建风险溢出网络时将每个资产视为同质化的，无需特别区分汇率、股票指数和商品期货，并且主要以溢出指数对应的网络中心度探讨风险溢出行为。

3实证研究

针对2000年以来外汇市场、股票市场和期货市场的27种资产，通过静态分析和滚动分析对大类资产的风险溢出展开分析。静态分析和滚动分析都包含4组实验，分别为8种汇率的外汇市场风险溢出研究、11种股票指数的股票市场风险溢出研究、6种大宗商品的商品期货市场风险溢出研究，以及27种资产的交叉风险溢出研究。在交叉风险溢出研究中，除8种货币汇率指数、11种股票指数和6种大宗商品外，还使用了美国10年期国债期货和美国VIX期货两种独特的期货。在实证研究中，首先对研究数据进行阐述，然后计算月度已实现波动率并进一步检验月度已实现波动率的平稳性，最后利用月度已实现波动率建立VAR模型研究风险溢出行为。

3.1研究数据

本研究从彭博系统获取全球主要经济体的外汇汇率、股票指数和大宗商品的历史数据，时间区间为2000年1月1日至2019年5月20日，共233个月，累计5 058天的日度数据。鉴于美元是世界主要存储和流通的货币，本研究重点研究8个国家或地区的货币兑美元的汇率，这些货币包括欧元EUR、英镑GBP、日元JPY、瑞士法郎CHF、澳元AUD、加元CAD、港币HKD和人民币CNY。后文将欧美汇率EUR/USD简写为EUR，其他汇率类似。所有汇率数据均为纽约时间每天下午5点的收盘价。

根据上述汇率覆盖的国家或地区，本研究获取11种有代表性的股票指数，具体为美国标普500指数(SPX)、欧元区斯托克价格指数(SX5E)、法国CAC400指数(CAC)、德国DAX30指数(DAX)、日本日经225指数(NKY)、香港恒生指数(HSI)、中国上证指数(SSEC)、加拿大标普TSX综合指数(SPTSX)、英国富时100指数(UKX)、澳大利亚综合指数(AS30)、瑞士股票指数(SMI)。

本研究考察的大宗商品包括伦敦金属交易所(LME)的金属期货(如黄金GOLD、白银SLVR、铜CU和铝AL)、伦敦洲际交易所(ICE)的布伦特原油期货(OIL)和芝加哥商品交易所(CME)的大豆期货(Y)。本研究选取的商品期货具有代表性，黄金和白银是具有避险功能的贵金属，铜和铝是重要的工业原料，原油是核心能源，大豆是全球性的农产品。本研究选用布伦特原油期货作为研究对象，是因为布伦特原油体系比美国WTI原油覆盖更大的交易量。此外，本研究增加了两种特殊期货品种，一种是美国10年期国债期货(T10Y)，它与美国10年期国债收益率关系密切；另一种是VIX期货，其标的是芝加哥期权交易所的恐慌指数VIX。

由于不同交易所的收盘时间不同，从彭博提取的股票指数和期货指数的收盘时间存在时差。但是由于本研究采用月度已实现波动率研究风险溢出效应，其结果受收盘价时间差异或日内波动行为差异影响很小。借鉴黄卓等[45]的研究，本研究利用日频数据估计上述8种汇率、11种股票指数、6种大宗商品和2种特殊期货的月度已实现波动率。为确保波动率的准确性，计算已实现波动的日频收益率rt，rt=100[log(ρt)-log(ρt-1)]。由于篇幅限制，本研究省略了上述资产价格走势和已实现波动率的描述性统计，如读者需要，可联系作者索取。月度已实现波动率的LB(20)检验结果表明，除大豆期货波动率外，其他所有资产均显著为0，说明已实现波动率不是白噪声序列，具有长记忆性和预测性。此外，ADF检验结果表明，除CNY外，其他所有资产在0.050水平上都显著，证明已实现波动率是平稳序列，满足VAR(p)建模条件。

3.2风险溢出行为的静态分析

根据不同资产的月度已实现波动率构建VAR(p)模型。VAR模型的广义预测误差方差分解需确定两个关键参数，即VAR模型阶数p和方差分解的步数H。借鉴梁琪等[38]的研究，VAR(p)模型的阶数p可根据赤池信息准则(AIC)确定。具体方法是取p为1～10依次计算AIC值，选择最小AIC值对应的p作为模型阶数。本研究根据全样本的统计实验发现AIC值最小时对应的阶数为3，即使用过去3个月的波动率预测下月波动率的表现较好。在计算广义脉冲响应函数时，随着向前预测步数H的变大，方差分解结果逐渐趋于稳定。本研究取H为1～10依次计算总风险溢出指数，发现当H取3时总风险溢出指数接近稳定值。综上分析，本研究选取p为3、H为3进行广义误差方差分解并计算溢出指数。

利用全样本数据，即233个月度已实现波动率序列作为静态数据，对当前时刻的VAR(3)模型进行参数估计，采用所估计VAR模型滚动向前预测3步，根据广义误差方差分解矩阵计算溢出指数。下面根据风险溢出表对风险溢出行为进行静态分析。

3.2.1 外汇市场的风险溢出

为了研究汇率之间的风险传染行为，对8种汇率波动构建VAR(p)模型进行预测误差方差分解，得到溢出指数，见表1。前8行8列为预测误差方差矩阵的元素，每行之和为100。矩阵每行数据表示某个资产的预测误差方差来源于不同资产的风险溢出比例，对角线上的数据表示某个资产来源于自身的风险溢出。

表1 外汇市场的风险溢出Table 1 Risk Spillover of Foreign Exchange Markets

注：括号中的数据为总风险溢出指数，下同。

由表1可知，①CNY、CHF、HKD和EUR这4种汇率受其他汇率的波动冲击很小，其预测误差方差更多来源于自身的风险溢出，普遍超过了85%。②CAD和AUD这2种汇率受其他汇率的波动冲击很大，分别高达85.587%和68.329%，它们主要受欧元和日元汇率波动冲击。③EUR和JPY的风险溢出最大，分别高达153.889%和61.513%，其他汇率的风险溢出较小。④EUR和JPY为正向的净风险溢出，表明欧美汇率对各国家或地区的波动冲击极为显著，佐证了USD和EUR仍然占据目前最重要的货币地位。⑤CNY和HKD汇率风险溢出较小，风险溢入也较小，说明人民币和港币的国际化有限。⑥欧元兑英镑的波动冲击为31.704%，反过来英镑对欧元的汇率风险溢出仅为0.210%，该现象佐证了广义误差方差分解矩阵的非对称性。

3.2.2 全球股市的风险溢出

为了研究全球股市之间的风险传染行为，对11个国家或地区的股票指数构建VAR(p)模型进行预测误差方差分解，得到风险溢出指数，见表2。由溢入指数可知，大多数全球股市受其他股市的风险传染较大，CAC、DAX、SPTSX、UKX和SMI等都超过90%，HSI和AS30超过80%，表明全球的股票市场联动性很强。然而，SPX的风险溢入仅为19.900%。观察方差分解矩阵元素可知，SPX主要承担了大部分风险溢出的角色，而受其他股市波动冲击较小。此外，SSEC受其他股市的风险溢入最小，仅为15.904%，反映其抵御风险的能力较高。

分析溢出指数发现，SPX、NKY、SX5E、DAX和SSEC的溢出指数较大，说明美国、日本、欧元区、德国和中国股市对全球股市具有较强的风险传染能力。值得强调的是，德国股市比法国股市具有更强的风险溢出效应。SPX的风险溢出异常显著，高达542.501%，反映美国股市是全球股市波动的最大源头。由净溢出指数可知，美国和中国股市为正向的净风险溢出，其他股市均为负，其原因与美国和中国为全球最大的两个经济体有关系。

通过表2可以探讨中国股市的风险传染关系。SPX对SSEC的风险溢出为3.507%，而SSEC对SPX的风险溢出为4.007%，说明在全样本的静态分析中中美股市的联动性较弱。与SSEC相比，SPX对HSI的风险溢出高达53.063%，而HSI对美国股市的风险溢出为0.234%，说明美国股市对香港股市的冲击较大，但是香港股市对美国股市的影响依然很弱。

3.2.3 大宗商品的风险溢出

为了研究大宗商品之间的风险传染行为，对6种大宗商品期货构建VAR(p)模型进行预测误差方差分解，得到溢出指数，见表3。关于大宗商品的溢入指数，铜受外部市场的冲击最大，主要源于黄金、白银和原油的风险溢入。铝的风险溢入为31.353%，主要受到铜、黄金和白银的波动冲击。白银主要受黄金的波动冲击。作为唯一的农产品期货，大豆期货的风险溢入最小。由此可见，伦敦金属期货存在很强的波动联动性。

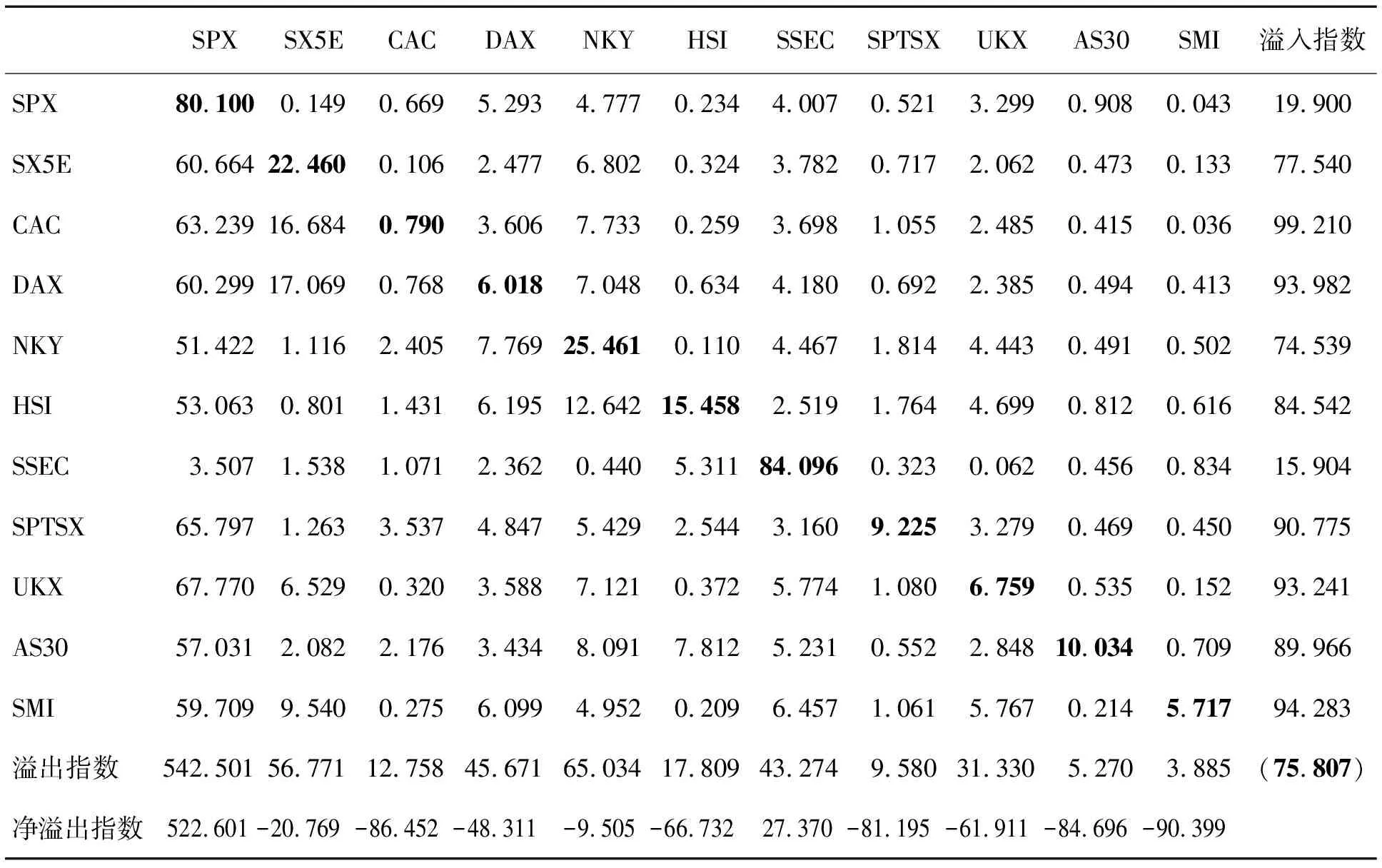
表2 全球股市的风险溢出Table 2 Risk Spillover of Global Stock Markets

表3 大宗商品的风险溢出Table 3 Risk Spillover of Commodities

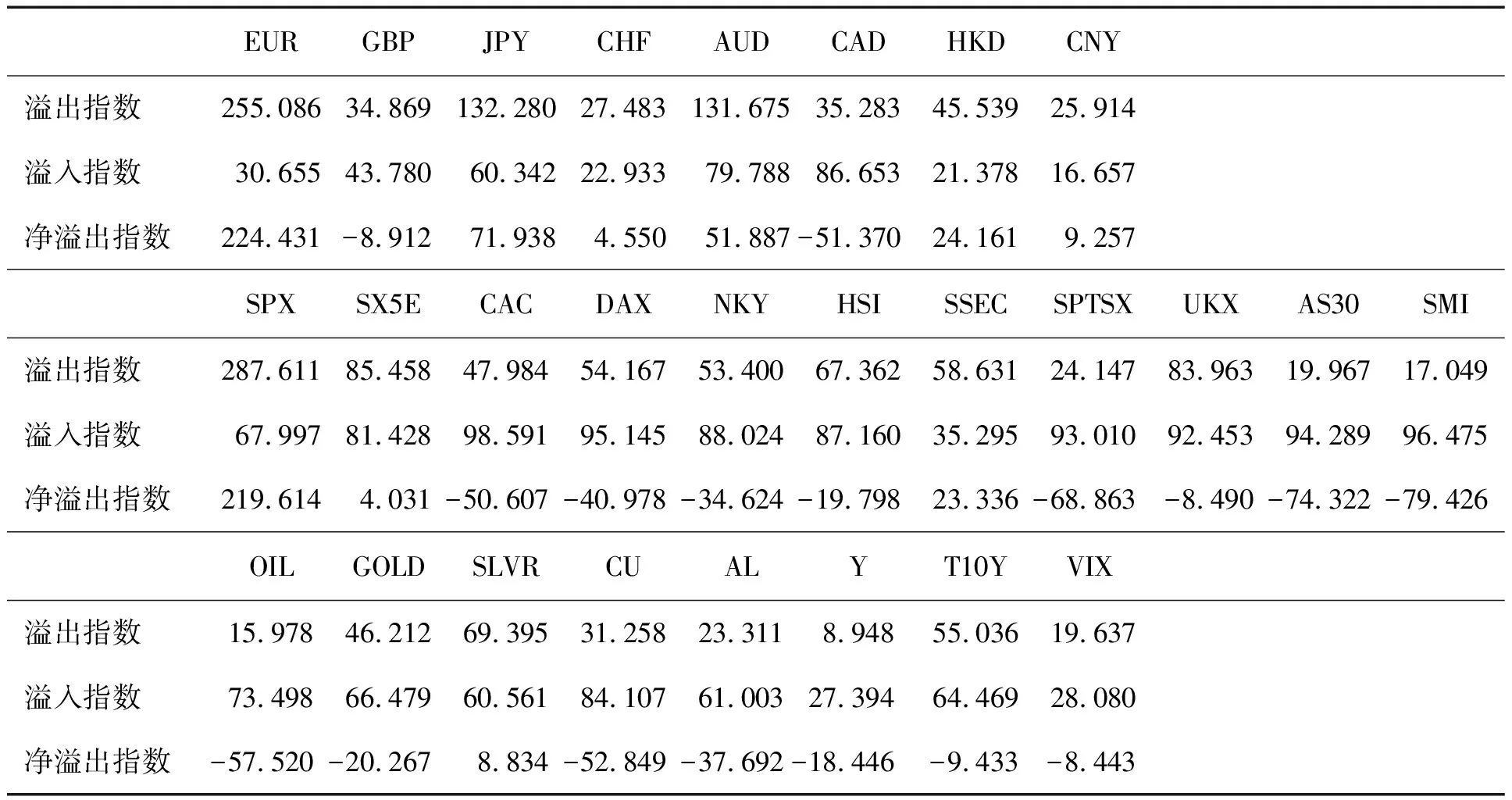
表4 多种资产的风险溢出Table 4 Risk Spillover for Various Assets

分析溢出指数可知，黄金对其他商品的风险溢出极为明显，达73.679%，白银的风险溢出也较大，为25.963%，可能与贵金属的避险保值功能有关系。分析净溢出指数可知，黄金和原油的净风险溢出为正。该数据证实原油波动具有较强的风险传染，这与原油是最重要的能源有关系。比较表1～表3的总风险溢出指数发现，全球股市之间的总风险溢出最大，为75.807%；全球汇市其次，为35.544%；而代表性商品期货相对较小，仅为26.538%。

3.2.4 多种资产的交叉溢出

为了探究不同资产之间的风险溢出行为，对27种资产构建VAR(p)模型进行预测误差方差分解，得到每个资产的溢入指数、溢出指数和净溢出指数，见表4， 27种资产包括8种外汇汇率、11种股票指数、8种商品期货。

由表4的溢入指数可知，汇率品种中溢入最小的是CNY和HKD，仅为16.657%和21.378%。而受到外部市场波动冲击较大的汇率为AUD和CAD，分别为79.788%和86.653%。该现象与表1较为相近。股票指数中溢入指数较小者为SSEC(35.295%)和SPX(69.997%)，其他9个股票指数均超过80%。该现象与表2比较接近。期货品种的溢入指数中，铜的风险溢入最大，为84.107%，大豆期货和VIX期货的风险溢入最小，约为28%。

分析表4的溢出指数可知，EUR和SPX的风险溢出最大，远超其他资产的风险溢出。汇率中溢出指数超过100%的还有JPY和AUD。期货品种中GOLD、SLVR和T10Y的风险溢出较大，其余资产的风险溢出较小。EUR的净溢出指数高达224.431%，SPX高达219.614%，充分体现了欧美汇率和美国股市为主要风险传染源。大部分汇率的净风险溢出都为正，说明外汇市场对全球金融市场具有强烈的风险溢出效应。除SPX以外，SSEC也是正向的净风险溢出，表明中美股市对全球金融市场具有较强的风险传染。

图1以广义预测误差方差矩阵作为连接矩阵构建了风险溢出网络，它可以直观揭示不同资产之间的风险溢出关系。该风险溢出网络具有27个节点、729条边，节点之间的连边代表资产之间的风险溢出，揭示了每个资产的风险溢出效应；节点的网络中心度越大(圆圈越大)，表示溢出指数越大；资产与资产之间的连边越粗，表示风险溢出越大；箭头表示风险溢出方向。

图1中，1为EUR，2为GBP，3为JPY，4为CHF，5为AUD，6为CAD，7为HKD，8为CNY，9为SPX，10为SX5E，11为CAC，12为DAX，13为NKY，14为HSI，15为SSEC，16为SPTSX，17为UKX，18为AS30，19为SMI，20为OIL，21为GOLD，22为SLVR，23为CU，24为AL，25为Y，26为T10Y，27为VIX。由图1可知，①SPX和欧美汇率的溢出指数最大。SPX几乎对大部分股票指数都产生较大波动冲击，而欧美汇率几乎对大部分汇率和股票指数具有波动冲击。②美国股市和欧美汇率对香港股市的波动冲击比上证指数更强。

综上所述，全球外汇市场、股票市场和期货市场之间具有很强的风险传染，其中欧美汇率和美国股市是最主要的风险传染源。

3.3风险溢出行为的滚动分析

前文根据风险溢出表对风险溢出行为进行了静态分析。然而，由于风险溢出指数具有时变特征，静态分析无法揭示波动传染的动态关系。本研究利用滚动时间窗的样本数据估计VAR(p)模型，进行广义误差方差分解，计算每个资产的时变风险溢出指数，并以此动态跟踪大类资产的风险溢出效应。

先对同类资产建立VAR(p)模型，然后再对所有资产建立VAR(p)模型。在同类资产构建VAR模型中，采用过去4年滚动时间窗数据(即48个月的已实现波动率序列)拟合VAR(3)模型参数，然后向前预测3个月的波动率构建广义误差方差分解矩阵，最终得到时变风险溢出指数。针对所有资产建立的VAR(3)模型，由于要预测的波动率变量高达27种，为了能够准确估计VAR(3)模型的参数，本研究将滚动时间窗定义为过去10年的已实现波动率序列，即120个月。

3.3.1 外汇市场的滚动溢出

风险溢出的滚动分析主要是跟踪溢入指数、溢出指数、净溢出指数和总溢出指数随时间的动态变化。以8种汇率已实现波动率作为变量建立VAR(p)模型，计算时变风险溢出指数和总风险溢出指数，具体结果见图2和图3。图2各子图分别包含溢出指数、溢入指数和净溢出指数。滚动时间起点为2004年1月，终点为2019年5月，累计185个月。

图2和图3表明4类指数都表现出明显的时变特征。图3总风险溢出指数为图2中所有溢出指数的平均值，它的变动范围为[50,90]，说明汇率之间的风险溢出指数之和是随时间变化的。观察8种汇率的溢入指数发现，CAD、AUD和CHF等资产频繁超过90%，说明这些品种承担了外部市场的大量风险冲击。欧美汇率的溢入指数长期较小，说明它受其他汇率品种波动冲击比较有限。

比较分析图2中不同汇率表现可知，EUR的风险溢出指数和净溢出指数一直很大，溢入指数非常小，说明欧美汇率在外汇市场中一直是最主要的风险溢出角色。GBP、JPY、CHF、AUD的净风险溢出指数存在阶段性的正负交替，说明这些汇率在外汇市场中阶段性地传染风险。CAD、HKD和CNY的净溢出指数长期为负，反映了这些汇率长期承受外部市场的风险传染，对外传播风险属于偶发性的。特别的，2016年上半年GBP暴跌，其净风险溢出超过300%；2015年CHF暴跌，其净风险溢出超过300%；2016年HKD暴涨，其净溢出指数突然超过100%。此外，CNY的净溢出指数从2014年开始呈现上升的态势，反映了CNY的国际化正在增强。

综上分析，欧美汇率是外汇市场中最主要的风险传染源，汇率的大幅涨跌容易对外传递风险，较多汇率长期承受风险冲击。

3.3.2 全球股市的滚动溢出

以11种股票指数的已实现波动率作为变量建立VAR(p)模型，以48个月作为滚动时间窗计算的时变风险溢出指数和总风险溢出指数见图4和图5。滚动时间的长度与3.3.1相同，累计185个月。

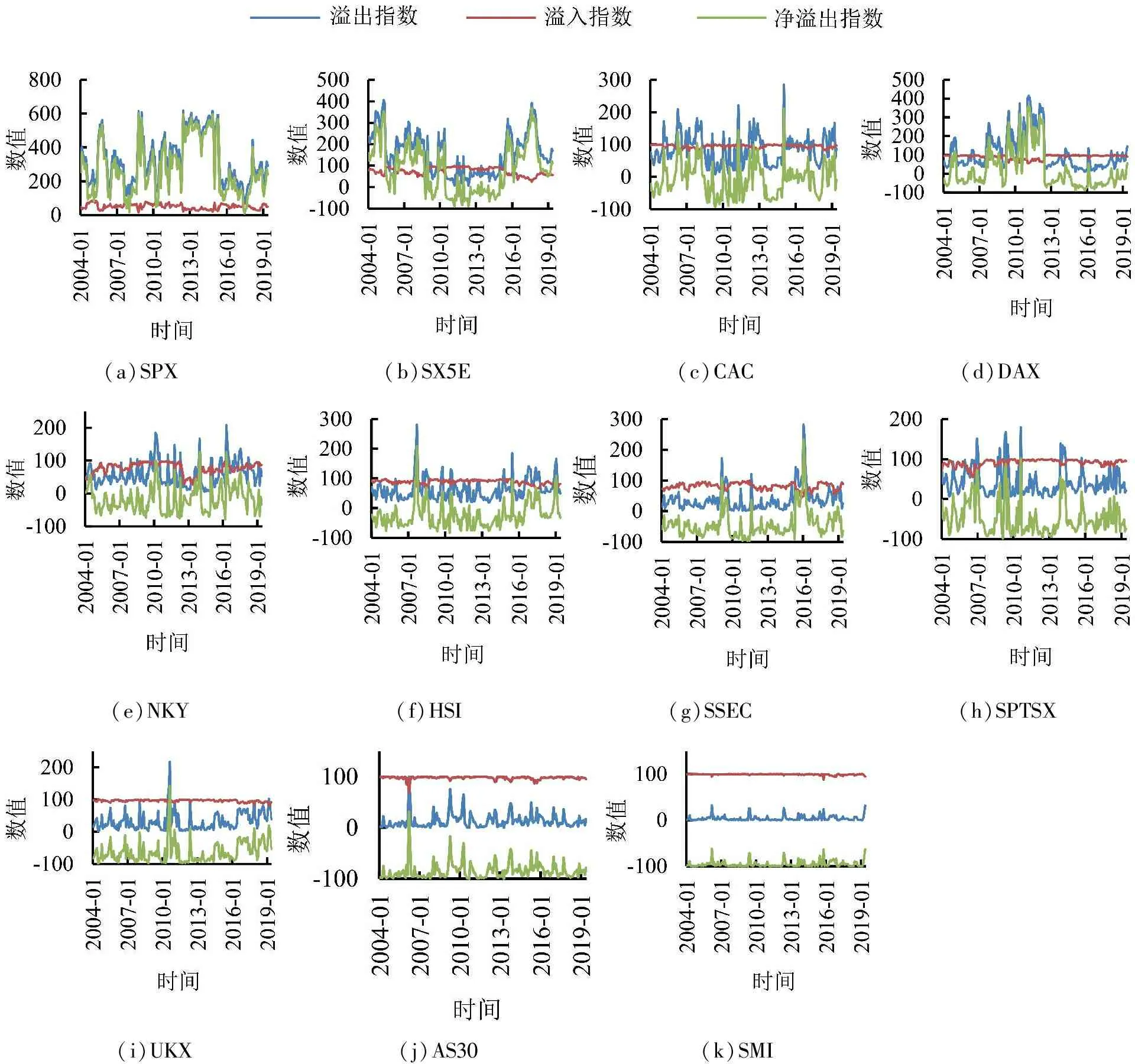
图4和图5表明全球股市的各类溢出指数也具有时变特征。图5表明股票市场的总溢出指数的变动范围为[80,90]，其变化范围比外汇市场小。由图4可知，SPX、SX5E、SSEC等市场的溢入指数相对较小，但是UKX、AS30、SMI、SPTSX、DAX、CAC等市场的溢入指数却相当高，长期靠近100%，说明这些股市主要承受外部市场风险冲击，扮演着趋势跟踪的角色。

(a)EUR(b)GBP(c)JPY(d)CHF(e)AUD(f)CAD(g)HKD(h)CNY

图2外汇市场的时变风险溢出指数
Figure 2Time-varying Risk Spillover Index of Foreign Exchange Markets

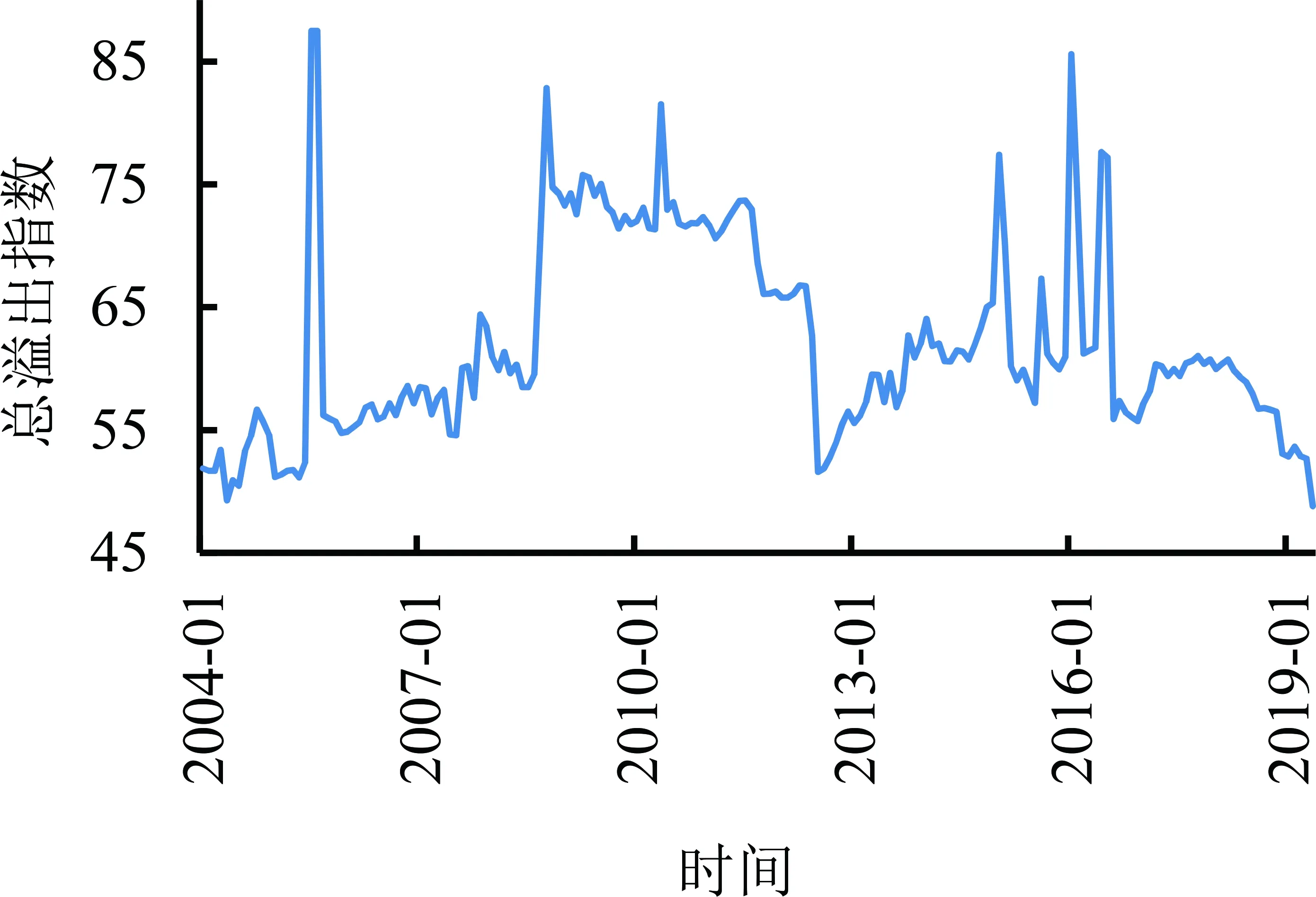
图3 外汇市场的时变总风险溢出指数Figure 3 Time-varying Total Risk Spillover Index of Foreign Exchange Markets

SPX的溢出指数和净溢出指数很大，长期在[100,600]之间，充分表明SPX在全球股市中一直是最主要的风险源。SX5E除2011年至2015年的净溢出指数为负外，其他时间主要表现为正向的风险溢出。尤其是2015年以后，SX5E在欧洲股市缓慢上涨过程中扮演着重要的引导角色。DAX在2009年至2012年的净风险溢出表现为正，表明2008年全球性股灾之后德国股市上涨最快。NKY、CAC、HSI和UKX阶段性发挥风险溢出效应。SSEC在2008年、2015年的两轮极端牛熊市(特别是熊市)对全球股市都产生了异常的风险冲击，其他时间区间主要接受全球股市的风险传染。此外，SMI和AS30受全球股市的风险溢入接近100%，很少对其他股市产生风险冲击。

综上分析，全球股市风险的联动性很强，而美国股市一直是全球股市的重要风险源。

3.3.3 大宗商品的滚动溢出

以6种商品期货指数的已实现波动率作为变量建立VAR(p)模型，以48个月作为滚动时间窗长度计算的时变风险溢出指数和总风险溢出指数见图6和图7。滚动时间的长度与3.3.1相同，累计185个月。

本研究选择的6种商品期货的各类溢出指数也是时变的，这些品种的总风险溢出指数在2012年以后呈现出逐渐下降的趋势。观察图6可以发现，6种商品的溢入指数均在50%上下徘徊，说明这些商品期货受自身的波动冲击较大。原油的溢出指数和净溢出指数长期在溢入指数的上方，体现了原油对其他5种商品具有持续性的风险溢出。原油在2010年至2012年、2016年至2019年的净溢出指数都出现大幅度攀升(超过100%)，这两段时间原油正处于强势的牛市周期，说明原油上涨对大宗商品冲击很大。黄金的净溢出指数在2013年至2017年呈现持续性上升，最高点达100%，这是因为黄金在2013年遇到大级别的行情背离，然后陷入了长达4年的大熊市。该现象反映黄金在熊市中对其他大宗商品产生了持续性的风险冲击。白银在2006年至2012年溢出指数持续性较大，在此期间白银开启了一轮长达6年的大牛市。铜、铝和大豆的净溢出指数长期为负值，体现了这3个品种长期接受外部市场的波动冲击，对外释放风险的机会不大。

(a)SPX(b)SX5E(c)CAC(d)DAX (e)NKY(f)HSI(g)SSEC(h)SPTSX(i)UKX(j)AS30(k)SMI

图4全球股市的时变风险溢出指数
Figure 4Time-varying Risk Spillover Index of Global Stock Markets

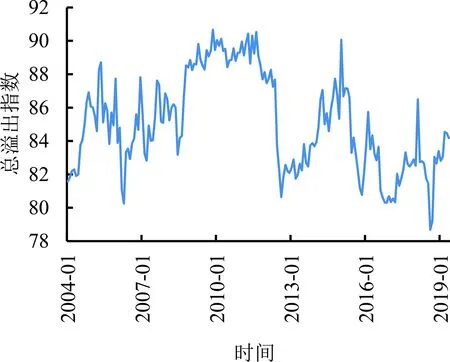
图5 全球股市的总风险溢出指数Figure 5 Total Risk Spillover Index of Global Stock Markets

综上分析，贵金属和原油期货在牛熊市中形成了持续性的风险溢出。

3.3.4 多种资产的交叉滚动溢出

以27种资产的已实现波动率作为变量建立VAR(p)模型，以120个月作为滚动时间窗计算各类溢出指数。滚动时间的起点为2010年1月，终点为2019年5月，累计113个月。由于篇幅限制，仅给出总溢出指数，见图8，其他时变风险溢出指数不予展示，如有需要可向作者索取。

(a)OIL(b)GOLD(c)SLVR (d)CU(e)AL(f)Y

图6大宗商品的时变风险溢出指数
Figure 6Time-varying Risk Spillover Index of Commodities

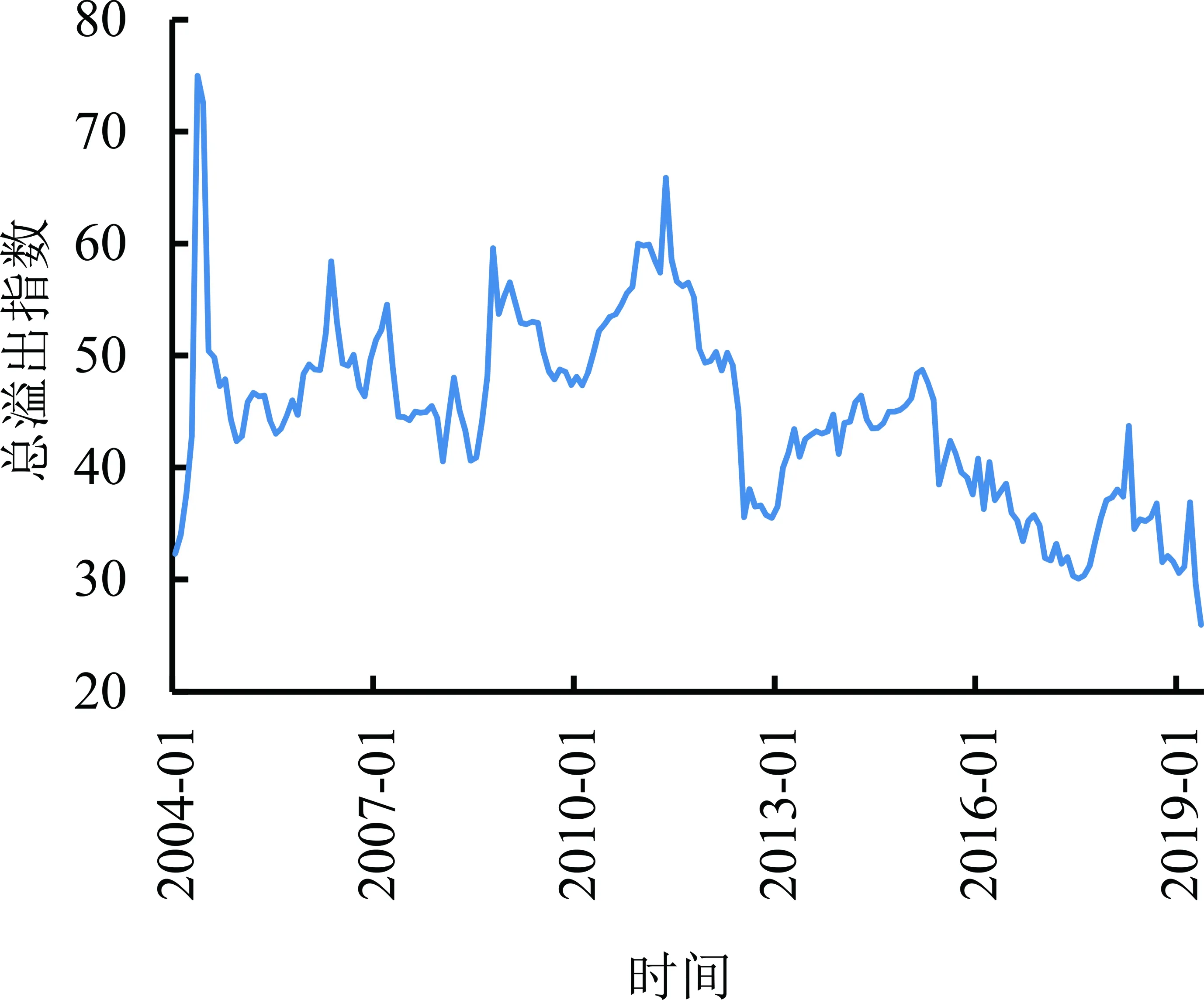
图7 大宗商品的总风险溢出指数Figure 7 Total Risk Spillover Index of Commodities

图8表明，2012年至2015年27个资产的总溢出指数呈现上升趋势，但2015年至今下降。总溢出指数于2015年出现峰值，分析时变风险溢出指数序列发现EUR和CHF两种汇率是风险溢出的主要角色，用金融风险溢出网络对其进行更加深入的探讨。①总溢出指数的峰值发生时点为2015年1月31日。②以27个资产作为网络节点，以广义预测误差方差矩阵作为连接矩阵，构建金融风险溢出网络，见图9，图中数字含义同图1。③风险溢出网络具有27个节点、729条边。网络中心度越大，表示该资产的风险溢出效应越大。风险溢出网络中圆圈较大的两个节点为CHF和EUR，二者的网络中心度(即溢出指数)最大，分别为852.315%和432.699%。

图8 大类资产的总风险溢出指数Figure 8 Total Risk Spillover Index of Large Class Assets

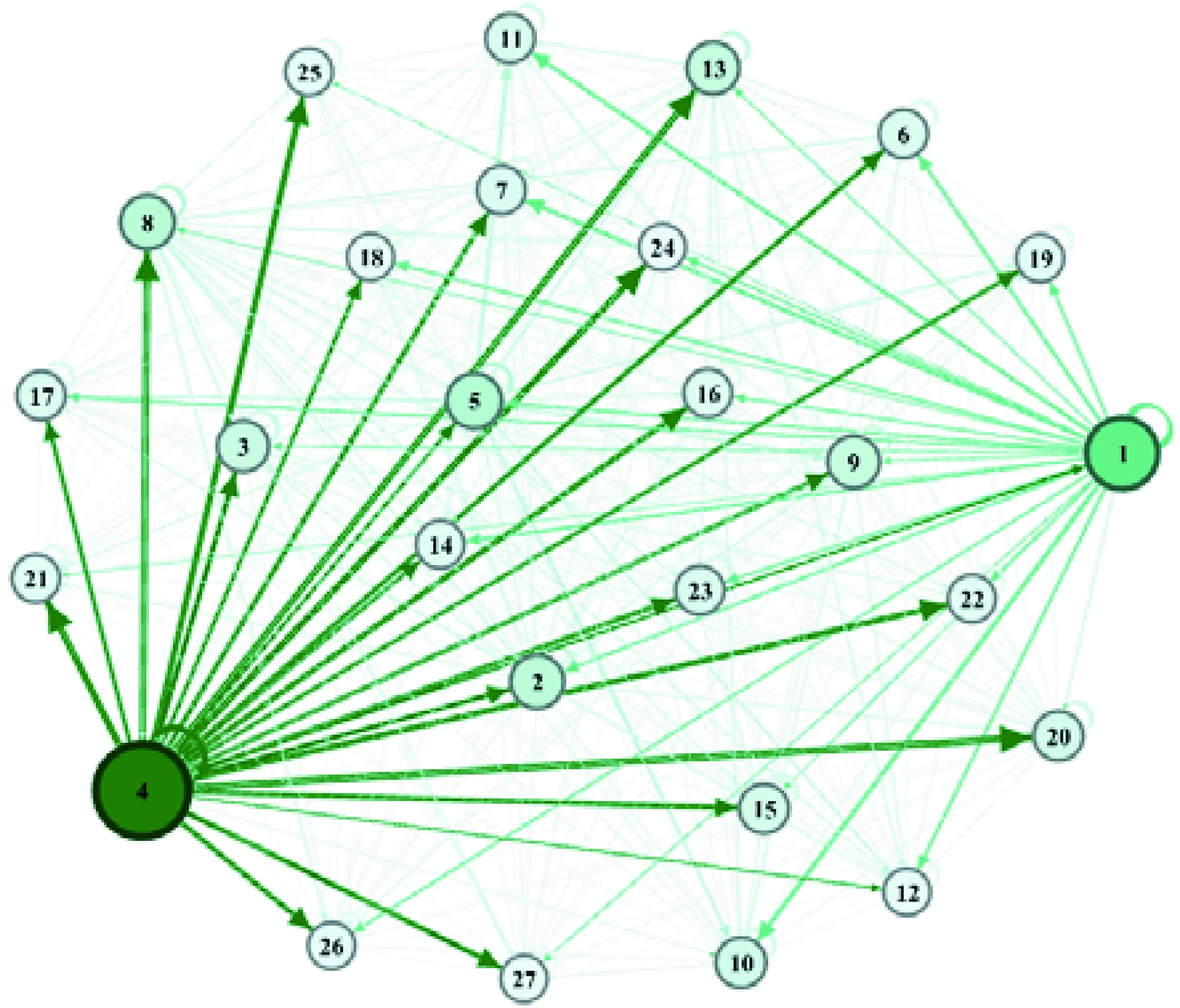
图9 总风险溢出指数峰值对应的风险溢出网络Figure 9 Risk Spillover Network Corresponding to the Peak of the Total Risk Spillover Index

根据不同资产的溢入指数分析可知，除汇率EUR、HKD、CNY和股票指数SSEC外，其他所有资产的溢入指数都很接近100%，说明股票市场、外汇市场和期货市场都长期受到外部市场的风险传染，体现了全球金融市场的风险联动性。关于外汇市场，大部分汇率都呈现阶段性的正向净风险溢出，表明汇率在全球金融市场扮演重要的风险传染角色。最显著的依然是欧美汇率EUR，其溢入指数最低，溢出指数和净溢出指数长期高达300%以上。JPY和AUD的溢出指数长期在100%以上，说明也发挥了风险溢出功能。HKD和CNY的溢入指数在50%左右，说明港币和人民币的汇率受外部市场冲击有限。与前文结果相似，CNY的净溢出指数在2016年后处于攀升阶段，说明人民币国际化趋势逐渐增强。

概括股市和商品的风险溢出行为，根据净溢出指数分析可知，净溢出指数阶段性为正的股市主要是SPX、HIS和SSEC。溢出指数长期超过100%的是SPX，说明美国股市持续性地对全球金融市场释放波动冲击。特别的，中国股市和香港股市在2015年的极端波动对外部市场造成了较为强烈的风险冲击。2010年以来，原油、贵金属等商品期货的风险溢出出现了脉冲式上涨，但长期来看大宗商品的净风险溢出皆表现为负，说明大宗商品对外部市场的风险传染十分有限。美国国债期货和VIX期货对其他资产的风险溢出很弱。

综上分析，全球金融市场的风险联动性很强，汇率对全球金融市场的风险溢出效应最强，欧美汇率和美国股市是重要风险源，期货市场的风险传染较弱。

4结论

本研究基于DY建模框架从全球视野研究大类资产的风险溢出行为，以资产的月度已实现波动率建立VAR模型，以广义误差方差分解矩阵构建有向溢出指数和风险溢出网络，并以此作为研究工具对大类资产进行风险溢出研究，考察外汇市场、股票市场和期货市场的27种重要资产，通过静态分析和滚动分析对大类资产的风险溢出效应进行实证研究。

研究结果表明，①各类资产的月度已实现波动率满足VAR建模的平稳性要求，为DY模型应用奠定了坚实基础。②通过研究8种兑换美元的汇率发现，外汇市场存在很强的风险溢出效应。欧美汇率是外汇市场最主要的风险传染源，其余汇率长期承受外部市场的风险传染，而对外传播风险属于偶发性；人民币汇率波动受外部冲击较小，它的溢出指数自2014年以来呈现上升态势，表明人民币的影响力正在增强。③通过研究11个全球股市发现，全球股市之间的联动性极强。美国股市一直是全球股市最重要的风险传染源，欧元区股票指数的风险溢出也很明显，其余股市长期承受外部股市的风险冲击。中国股市在2008年和2016年暴跌过程中对其他股市造成了较大的风险冲击。④通过研究6种商品期货发现，伦敦金属期货之间存在较强的风险溢出效应。作为最重要的能源，原油期货具有较强的风险溢出能力。作为具有保值避险功能的贵金属，黄金和白银期货在大型牛熊市中产生了持续性的风险传染。⑤通过研究27种资产的交叉溢出发现，全球外汇市场、股票市场和期货市场之间具有很强的风险溢出关系。汇率对全球金融市场的风险溢出效应最强，美国股市对全球市场具有持续性的风险冲击，包括美国国债期货和VIX期货在内的期货品种对外部市场的风险传染能力较弱。

本研究在理论、实务和政策上都有重要启示。理论方面，①本研究采用不受变量顺序影响的DY框架计算有向溢出指数，得到的风险溢入指数、风险溢出指数和净溢出指数存在时变性，它们为风险溢出行为提供了滚动分析工具。②广义误差方差分解矩阵存在非对称性，可直接用于构建金融风险溢出网络，它为大类资产的风险传染行为提供了直观分析工具。实务方面，①本研究证实全球股票市场的风险联动性很强，而且各国股市一定程度上都受到美国股市的波动冲击。因此，在股票投资决策中应该特别重视美国股市的风险传染。②本研究结果也表明外汇市场对股票市场具有重要的风险冲击。当欧美汇率或者人民币兑换美元汇率产生异常波动时，股票投资决策应该充分重视汇率波动风险。政策方面，①随着人民币国际化，人民币汇率的波动备受关注。本研究深入研究了人民币汇率在外汇市场中的风险溢入和风险溢出的历史表现，相关结论可为中国制定汇率政策提供经验证据。②随着中国股市的不断开放，尤其是外资额度的放宽，中外股市的联动性会持续增强。在此背景下，利用本研究方法持续跟踪中外股市风险传染，对制定防范股市风险的相应政策具有重要意义。

本研究也存在局限性。①本研究基于月度已实现波动率研究大类资产的长期风险溢出效应，尚未研究短期风险溢出效应。②由于DY研究框架已被证实具有很高稳健性[12-13,20-21]，本研究弱化了对DY研究框架的稳健性讨论。③风险溢出网络的应用价值很大，本研究仅将其用来追溯风险源，尚未考虑它在投资策略方面的价值。有鉴于此，未来研究可探讨金融市场的短期风险溢出效应，从而更加及时地捕捉到重大的事件性风险冲击，还可以基于风险溢出网络的网络中心度研究资产定价和大类资产配置方法。