基于蒙特卡罗法的水下激光光幕探测性能研究

杨 曈，王 凡，倪晋平，曾 辉

(西安工业大学 陕西省光电测试与仪器技术重点实验室 陕西 西安 710021)

引言

随着海洋水资源的开发利用日益深入，以及领海权军事需求的迫切性，水下装备及水下武器的研制开发与测试[1]受到日益关注。光幕靶作为陆上性能稳定常用的飞行弹丸动态参数测量装置[2]，将其用于水下测量，有助于提高水下武器的测试水平[3]。水下光幕探测性能分析对水下光幕靶的研制尤为重要。目前有关水下光幕的设计及性能分析的研究报道较少，考虑到水下环境的复杂性和激光光源的准直性[4]，本文拟对影响水下激光光幕传输的海水参数、初始功率、传输距离进行分析研究，为水下激光探测光幕的研制奠定基础。

水下光传输特性是研究热点之一，国内外学者做了大量研究工作。Damush等人得出了水下传输光场的解析解，Paul F.Schippnick等人采用唯象方程法，计算出了水下光场辐射能量的分布，但这些传统解析法的理论模型都对介质情况作了大量的简化处理，与实际情况存在着较大的差距[5]。周田华等人[6]研究了影响水下激光穿过海气界面后的光场分布情况；詹恩奇等人[7]研究了光在大气和海水信道中传输的能量衰减；以上研究均讨论了光在海气界面中的传输。对光的垂直传播进行的研究分析，并未对光在水中水平传输情况开展研究。刘娟等人[8]研究了受激布里渊散射对激光在水中衰减特性的影响。为进一步研究激光在水中的传输规律提供了可靠的基础，但仅讨论了散射的影响，没有考虑如吸收等因素对激光在水中传输的影响。针对以上问题，本文采用了蒙特卡罗模拟方法[9]，构建了水下激光光幕在水中的传输模型，分析了水下激光光幕在水平传输过程中的功率衰减情况。仿真比较了传输距离，初始功率、海水衰减系数(衰减系数)三者因素对水下激光光幕传输的影响，定量分析了水下激光光幕的性能。

1 水下激光光幕的工作原理

探测光幕[10]有3部分：光源、受约束的传播空间和光电接收装置。图1为水下激光光幕的示意图，采用激光光源为光源端，激光/光敏接收器为光电接收端，光源端和接收端之间形成了受拘束的水下光传播空间，组成了具有探测性能的水下激光光幕。

本文所研究的水下激光光幕主要用来探测在水下有无物体从光幕中通过。在接收端，除了光敏接收器外还有信号放大电路。没有物体通过时，光电敏感器件上的光通量保持恒定；当有物体通过时，光电敏感器件上的光通量发生变化，变化的光通量通过信号放大电路转为光电流信号，并输出一个电压脉冲信号。有无信号的产生，可以判断是否有物体通过光幕。

水下激光光幕与陆上激光光幕相比，设计时需要综合考虑水下复杂环境的影响，例如在结构设计时，需要考虑防水性和抗压性等。同时，光在水的散射、吸收从而导致光幕在水下传输时，会产生严重衰减，其探测距离受到了较大影响。

图1 水下激光光幕示意图Fig.1 Schematic of underwater laser screen

2 影响水下激光光幕探测性能的因素

由于海水中的复杂环境和各方面因素，与在大气中相比，光束在海水中的传输过程更加复杂。光在海水中因受到吸收和散射作用从而发生衰减，使得光在传输过程中功率不断减弱。根据查阅到的文献可知，在波长为460 nm～520 nm之间的蓝绿光波段[11]，激光在水下受到吸收和散射的影响最小。因此，采用蓝绿激光作为水下激光光幕的光源端最为合适。

海洋的光学特性与散射介质的分布密切相关，研究者们通过长期的测量，将海水划分为3种海水类型[12]，大洋水体称为1类水体，沿岸水体称为3类水体，介于沿岸水体和大洋水体之间的称为2类水体。它们的光学特性可以用表1来表示。

不同的海水类型，具有不同衰减系数，对于水下光的传输具有一定的影响，除此之外，水下激光光幕中光源端发出的光在水中传输时，也会受到初始功率、传输距离的影响。因此，本文主要分析影响水下激光光幕探测性能的海水衰减系数、初始功率及传输距离这三者因素。

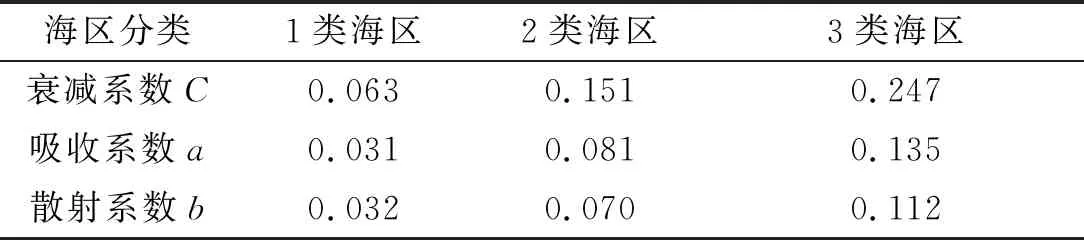
表1 海水衰减、吸收、散射系数分布表

3 水下激光光幕探测性能建模

3.1 蒙特卡罗法构建模型流程

蒙特卡罗方法是通过大量的随机样本模拟某一物理过程并得到统计规律。本文采用蒙特卡罗方法构建模型的流程如图2所示，光在水中发生散射的过程，可视为光子在水中的传输问题[13]，其主要包括：光子步长的确定、光子的运动、光子是否到达接收面等一系列过程。

图2 蒙特卡罗方法构建模型流程图Fig.2 Modeling flow chart of Monte Carlo method

3.2 构建模型的条件

3.2.1 光子步长的确定

光子步长即两次碰撞之间光子在介质中所走的距离，光子步长的大小与水体的衰减系数密切相关，水体的衰减系数越大，光子的步长越小[14]。将光子步长设为l，则l=-(1/C)lnR，其中C为水体的衰减系数，R为(0,1)之间均匀分布的随机数。

3.2.2 光子的运动

如图3所示，建立三维直角坐标，设光子的起始坐标为(x,y,z)(定为坐标原点)，光子行进的方向为(Ux,Uy,Uz)。

图3 光子运动坐标的建立Fig.3 Establishment of photon motion coordinate

光子从坐标原点位置发出，根据光子步长，可以得到光子的运动方向：

(1)

(2)

根据公式(1)和(2)，确定了光子在水中的运动方向。

3.2.3 光子的吸收和散射

由概率P吸收=a/(a+b)、P散射=b/(a+b)和0～1之间的随机数R进行比较，当R≤P吸收时，光子发生吸收，认为光子“生命结束”。当R≥P散射时，光子发生散射，需要重新确定光子的方向(X′，Y′，Z′)。

在散射过程中，光子方向的改变由散射角和方位角来确定，散射角表示散射之后的新方向与原始方向之间的夹角，方位角表示相对于一个参考方向，散射在平面上投影改变的角度。

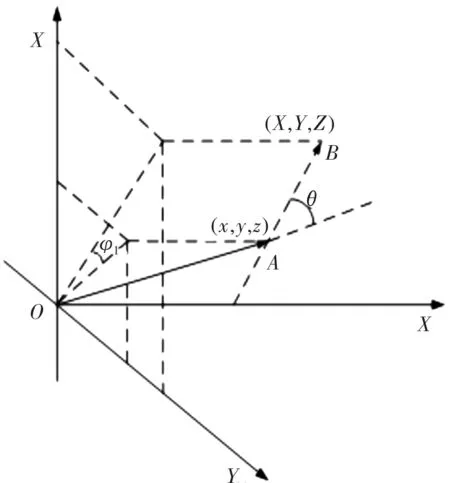
图4 散射过程中光子运动坐标表示Fig.4 Coordinate representation of photon motion inscattering process

如图4所示，θ为散射角，φ1为方位角，本文仅考虑米氏散射的影响。散射角由散射相函数(HG散射相函数)表示：

(3)

式中：g为不对称因子，根据研究，当g=0.924时，HG函数的拟合度最高[15]。R3为(0,1)之间的均匀分布随机数；方位角φ1=2πR4，R4也为(0,1)之间的均匀分布随机数。

(4)

3.2.4 到达接收面的判断

光子在发生散射时，是一种碰撞过程。每发生一次碰撞，功率就损失一次，假设所有光子的初始权重W均为1，发生散射的功率损失系数为(b/C)，发生n次散射后的权重Wn与n-1次散射后的权重Wn-1满足Wn=Wn-1(b/C)。当光子发生多次散射后，权重衰减到很小时，默认光子消亡。在此设定一个极限权重阈值，在发生每一次散射之后，将计算出的光子权重值与极限权重阈值进行比较，低于阈值，则不再进行统计。光子经过一系列的运动过程，最终判断光子的坐标值在Z方向是否大于设定的距离，当大于设定距离时，光子所在的位置在接收器接收面范围内，则判断光子被接收。反之未被接收。

4 水下激光光幕传输模型仿真

根据构建的水下激光光幕传输模型，针对不同的条件对其进行仿真。设光子数N为106，则每个光子的初始功率为P总/N。根据图2的仿真流程，利用MATLAB软件编写程序，将最终到达探测端的光子能量进行叠加后求和，便可得到最终到达探测端的功率P1。最终的传输率即为P1/P总。采用蒙特卡罗方法，其中含有较多的随机数，每次仿真的结果均有偏差，因此，对每个条件均仿真了50次，对其求平均值。

4.1 海水衰减系数的影响

设传输距离为1 m，初始传输功率为15 W，则每个光子的初始功率为15/106。如图5所示，为50次结果的直方图，可以看出最终功率P1的平均值约为2.3，则传输率P1/P总=0.153 33。为了表示仿真结果的准确性，在后续仿真中，均采用50次结果的平均值。

图5 最终功率50次结果直方图Fig.5 Histogram of final power50times results

图6所示为三类海水类型的衰减系数所对应的传输率，随着衰减系数的增加，传输率不断减小，仿真结果表明，海洋水体越清澈，衰减系数越小，光在传输过程中所受的影响越小，最终到达探测端的功率越大。

图6 三类海水类型衰减系数的传输率Fig.6 Transmission rate of attenuation coefficient of threetypes of seawater

4.2 初始功率的影响

设传输距离为1 m，海水衰减系数选取一类水体，C=0.063，a=0.031，b=0.032；光子数N为106，改变初始功率的大小，如图7(a)所示，为最终功率随初始功率的变化图，随着初始功率的增加，最终的功率也随之增加。由图7(b)可以看出，随着初始功率的增加，传输率的变化不大。由此，在后续设计水下激光光幕光源端时，在传输距离一定时，选择功率适中的光源即可。

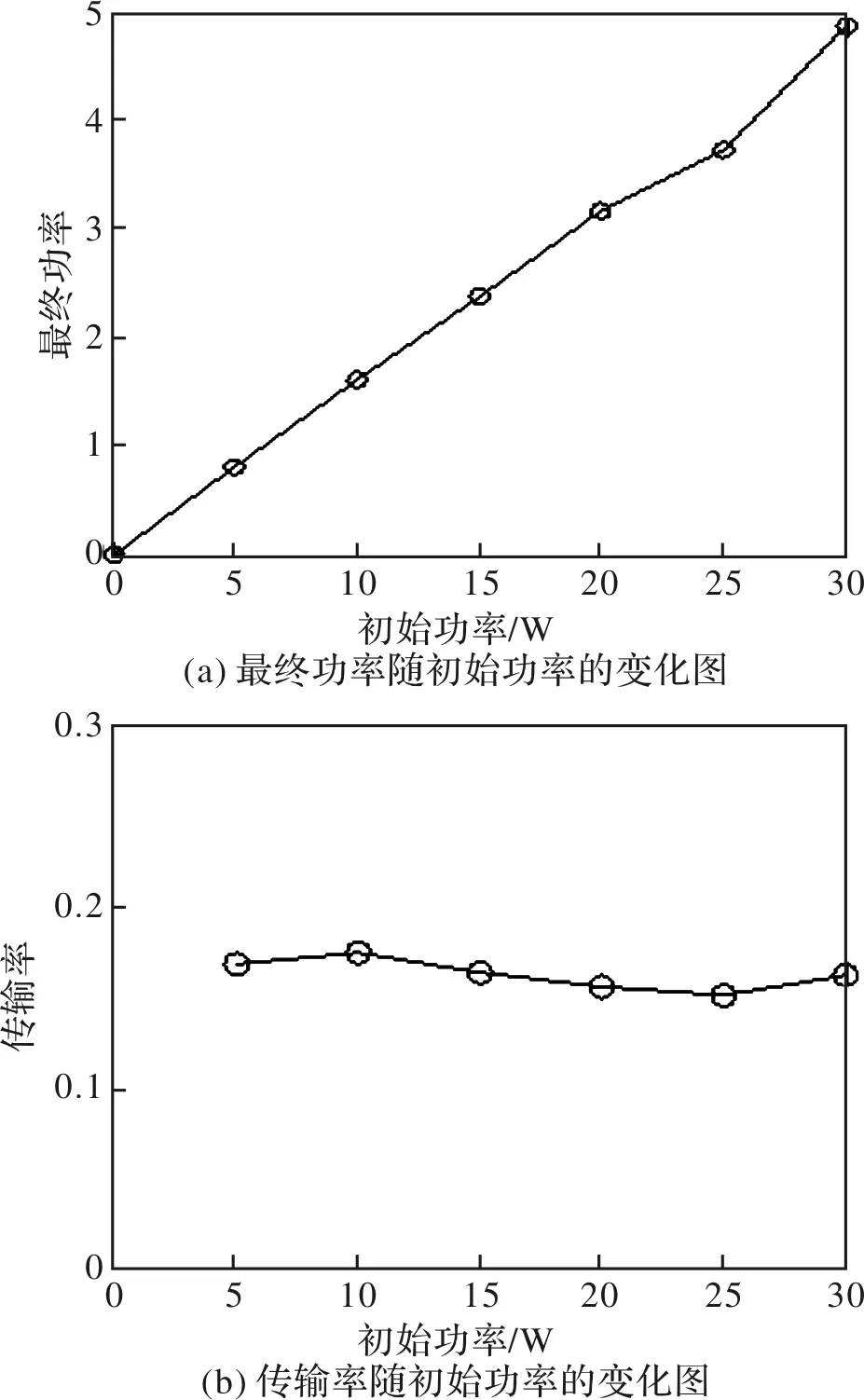
图7 初始功率的影响图Fig.7 Influence diagram of initial power

4.3 传输距离的影响

设传输初始功率P总为15 W，海水衰减系数选取一类水体，C=0.063，a=0.031，b=0.032，光子数N为106。改变传输的距离，当L=1 m时，每个光子的功率及坐标分布的单次仿真结果如图8所示。当光子功率为零时，无法到达探测端，除此之外，其他光子均可到达探测端。

图8 L=1m光子能量及坐标分布Fig.8 Energy and coordinate distribution ofL=1m photon

为了更好地显示到达探测端每个光子的坐标，仅将到达探测端的光子坐标表示出来，如图9所示，大多数光子集中在(0,0)点附近，即从坐标原点发出的光束，除了功率的衰减，最终大部分也会到达探测端的原点。当光束在水中传输时，其功率会发生衰减，但传输方向变化不大。

图9 探测端光子坐标分布Fig.9 Probe end photon coordinate distribution

增加传输距离，如图10所示，为L=10 m时每个光子的功率及坐标分布，对比图8可以看出，最终到达探测端的光子数有所减少，但其位置分布情况变化不大。

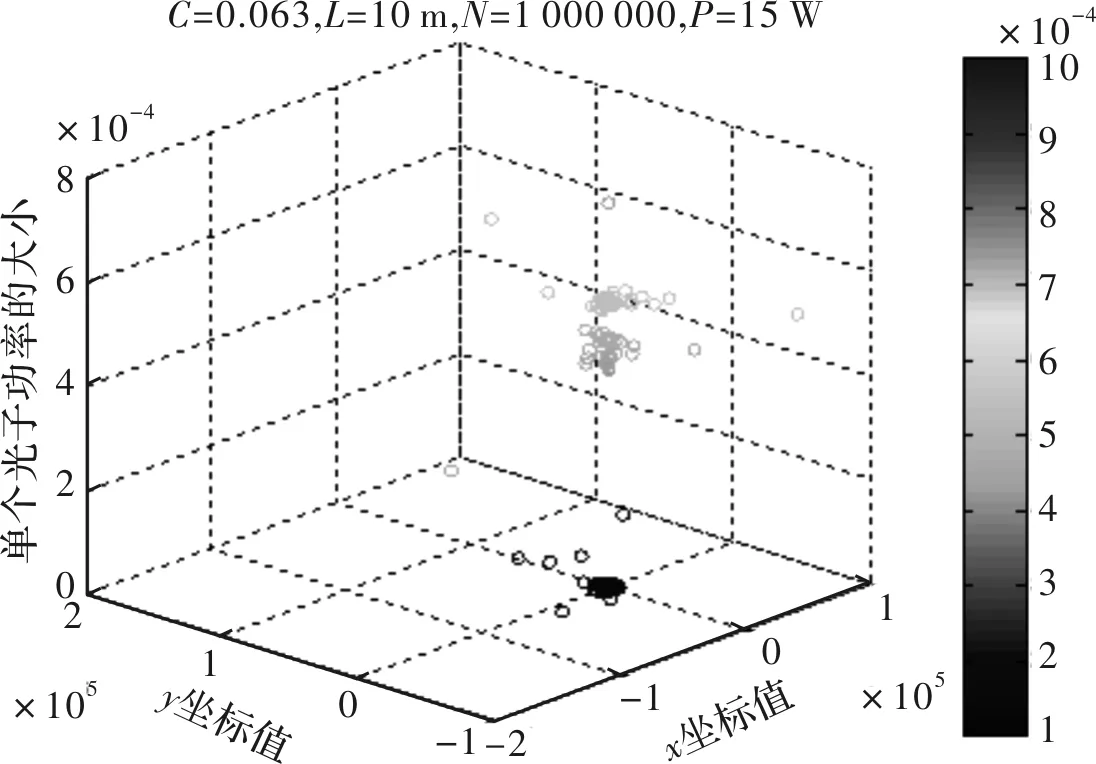
图10 L=10m光子能量及坐标分布Fig.10 Energy and coordinate distribution ofL=10mphoton

如图11所示，为传输率随传输距离的变化图，由图可以得到：当传输距离在1 m时，传输率变化不大，在15%左右。当传输距离增加时，到达探测端的功率发生衰减，传输率下降，传输距离增加到30 m时，传输率在5%以下。

图11 传输率随传输距离的变化图Fig.11 Change of transmission rate with transmissiondistance

5 结论

本文基于蒙特卡罗模拟方法，构建了水下激光光幕传输模型，并对其进行了较为全面的定量分析。仿真比较了传输距离，初始功率以及海水衰减系数对水下激光光幕探测性能传输的影响。仿真结果显示：海水的衰减系数越小，即海水越清澈，其传输率越高，在大洋水体中，水下激光光幕受到的影响最小。在一定的海水衰减系数和传输距离下，初始功率的增加，仅对最终到达探测端的最终功率有影响，对传输率影响不大。因此，在一定条件下，选择功率适中的激光光源。当海水衰减系数一定，传输距离在1 m时，其传输率变化最稳定，在15%左右，传输距离增加到3 m时，传输率在13%左右，当传输距离增加到10 m时，传输率下降到了10%，传输距离增加到30 m时，传输率在5%以下。因此，在设计水下激光光幕时，光源与探测端距离在1 m～3 m最为合适。

文中研究的结果可以为下一步设计水下激光光幕提供理论参考。