从光学极值思想到最速降线问题

马文东

(江苏省淮北中学 223900)

1 几何光学的发展

光的反射的研究，最早可以追溯到古希腊学者欧几里得(Euclid of Alexandria ，前330年～前275年)，在一本主要研究平面镜、凹面镜和凸面镜反射问题的《镜面反射》著作中，记录了入射光线和镜面的夹角等于反射光线与镜面的夹角[1].约在公元100年，亚历山大里亚的希罗为了解释光的直线传播和反射定律,曾经提出过光在两点之间走最短路程的看法.

对光的折射现象的研究要稍晚一些，古希腊人托勒密(Claudius Ptolemaeus，约90年～168年)首先通过实验研究了光的折射现象，根据正确的测量数据，得出一个只有在入射角很小的情况下才近似成立的结论：折射角和入射角是成正比关系.

德国人开普勒(Johannes Kepler， 1571～1630)在托勒密实验的基础上，经过分析当时所知道的光学成果，发现了托勒密关于折射规律结论的局限性，得出了他的折射规律是：折射角由两部分组成，一部分正比于入射角，另一部分正比于入射角的正割,只有在入射角小于30°时，入射角和折射角成正比的关系才成立.

荷兰数学家斯涅耳(Willebrord Snell，1580～1626)于1620年前后，通过实验确立了开普勒想发现而没有能够发现的折射定律： 在不同的介质里，入射角和折射角的余割之比总是保持相同的值.后经法国人笛卡尔(Rene Descartes，1596～1650年)，给出了折射定律的现代表述形式.

1650年法国数学家费马(Pierre de Fermat，1601～1665)，把光的直线传播、反射和折射定律等光学的基本实验定律，总结成为一个原理：光由空间一点传播到另一点，将沿着光程(作用量)为极值的路径传播.

2 几何光学中的极值问题(Fermat原理)

2.1 光的反射

光的反射取光程极小(同种介质中也是时间最短)的路径.

例1平面镜的反射,光程取极小值的情况：

如图1所示，光从A点发出，在O点反射经过B点，光程LAOB取极小值，作AO的镜像A′O，容易看到A′B为一条直线段，两点之间线段最短.如果从A到B的光路不经过O点，而是经过O′点，那么A′B变为折线，此时光路LAO′B，很明显，光程LAO′B>LAOB.

2.2 光的折射

折射光线也有光程取极值路径的性质.

图2

因此，只需证明

n1·LAC+n2·LCB为最小值即可.

根据数学中求极值的方法，令上式对x的微分等于零可得

3 最速降线问题

3.1 问题的表述

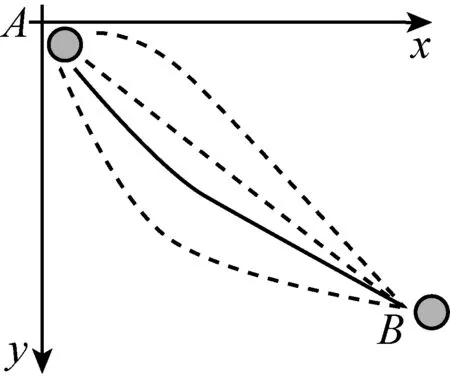
图3

伽利略在1630年提出的问题：如图3所示，一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，问沿着什么曲线滑下所需时间最短.

伽利略猜测这曲线是圆，可是这个答案只比直线要接近真实，还不是所要求的正确答案.

3.2 问题的解答

瑞士数学家约翰·伯努利(Johann Bernoulli)在1696年6月号的《教师学报》上重新提出了这个最速降线的问题并征求解答.到第二年有几位数学家得到了正确答案，其中包括牛顿、莱布尼兹、洛必达和伯努利家族的成员.

约翰·伯努利和牛顿的解答思路[2]：

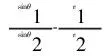
下面根据约翰·伯努利和牛顿的解答思路，较详细介绍一下问题的解答过程：

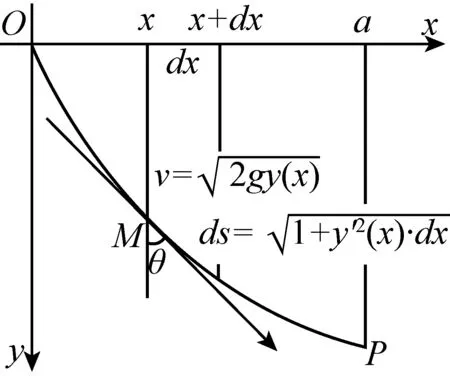
图4

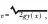
(1)

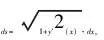
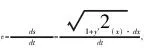
(2)

由(1)和(2)可以得出，运动小球所经过的时间为

(3)

从T的表达式可以看出，T是依赖于函数y=y(x)的函数，y=y(x)取不同的函数，T也就有不同的值与之对应.

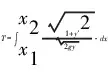
对式(3)中y=y(x)的求解方法，文献[3,4]多采用Euler方程的求解方法，而Euler方程的推导过程比较复杂，这里我们用一个相对较简单的方法得出问题的解.

(4)

把(1)式代入(4)式，整理后得

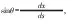
令y′=cotθ，

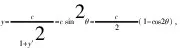
又因为

积分得

由边界条件y(0)=0，得c1=0.

令t=2θ,则

图5

伯努利和牛顿的解答,将引力场中的力学问题与光学问题进行的类比，带给人们以极大的启发性，该问题本身导致了变分法的创立，从而为泛函极值的求解提供了普遍方法.