均布自重下椭圆环的内力和位移分析

黄开志 陈小亮 张龙 郑恒伟 李定玉

(重庆科技学院建筑工程学院， 重庆 401331)

相关研究显示，超高精密传感器件、精密机电产品及土建结构等受自重的影响较大[1-6]。杨实如运用材料力学假设，求出了小曲率圆环挠曲线微分方程的通解，并以实例说明如何利用所求通解计算圆环的内力及位移[7]。王兆清采用重心插值配点法求解了圆环的位移及稳定性[8]。彭美骥根据圆环变形的假设条件，用叠加原理推证了圆环振动时环上任意点的位移[9]。关于圆环在诸如集中力、集中力偶、静水压力、双向均布对压等载荷下的内力和位移计算，现有研究文献较多。

马少华对椭圆环在双向均布对压下的内力和位移进行了计算[10]。分析椭圆环的内力和位移，对该类产品的设计制造、安装调试和维护保养等具有一定的意义，但相关文献较少。本次研究未采用求解微分方程的办法，而是借助重心公式，由能量法导出闭口和顶部开口椭圆环的内力和位移计算公式，并举例对求解结果进行分析。

1 公式推导

1.1 闭口椭圆环

图1所示力学模型中，均质等截面线弹性闭口椭圆环放置在水平面上，受均布自重q作用，关于AB轴对称，则A截面剪力为零，其为二次超静定问题。

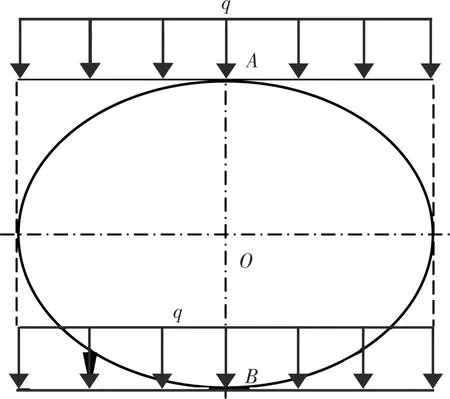
图1 力学模型

1.1.1 内力

在图2所示原载荷下的内力图中，X1和X2为多余反力。设椭圆参数方程为：

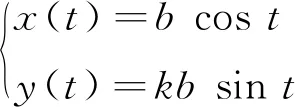
(1)

离心角为φ的P点，其切线和法线斜率满足：

结合式(1)，得式(2)：

(2)

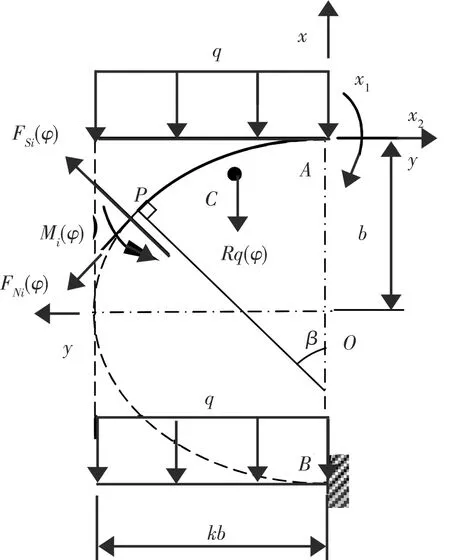
图2 原载荷下的内力

离心角为α的点的弧坐标s(α)满足：

结合式(1),得式(3)：

(3)

AP段的重心C坐标为：

结合式(1)(3)，得式(4)：

(4)

计算AP段均布自重q的合力：

结合式(3)得：

(5)

计算P截面上由q引起的内力：

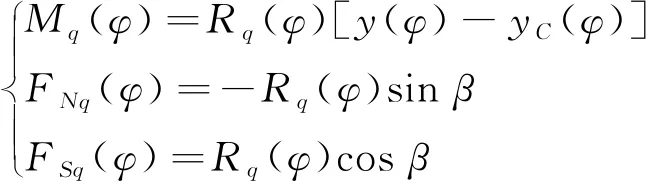
由式(1)(2)(4)(5)得式(6)

(6)

计算P截面上由x1和x2引起的内力：

结合式(1)、(2)，得：

(7)

将式(6)和(7)对应项相加，得P截面上的总内力：

(8)

计算与弯矩对应的应变能：

(9)

A截面的转角和沿轴线的位移均为0，由卡氏第二定理得式(10)：

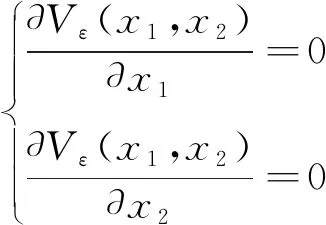
(10)

由式(8)、(9)、(10)得式(11)：

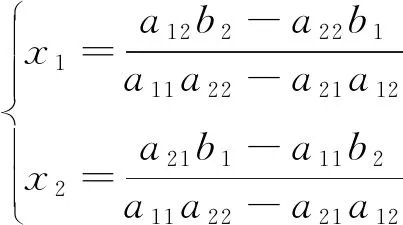
(11)

其中：

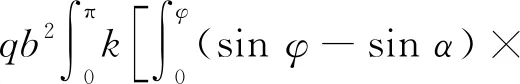
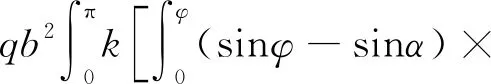
将式(11)代入式(8)，可求得内力。

1.1.2 位移

在图3所示单位载荷下的内力图中，P截面分别虚加单位载荷Fx(φ)=1,Fy(φ)=1和Me(φ)=1时,在离心角为θ的Q截面引起的弯矩，依次为：

(12)

式中，θ∈[φ,π]。

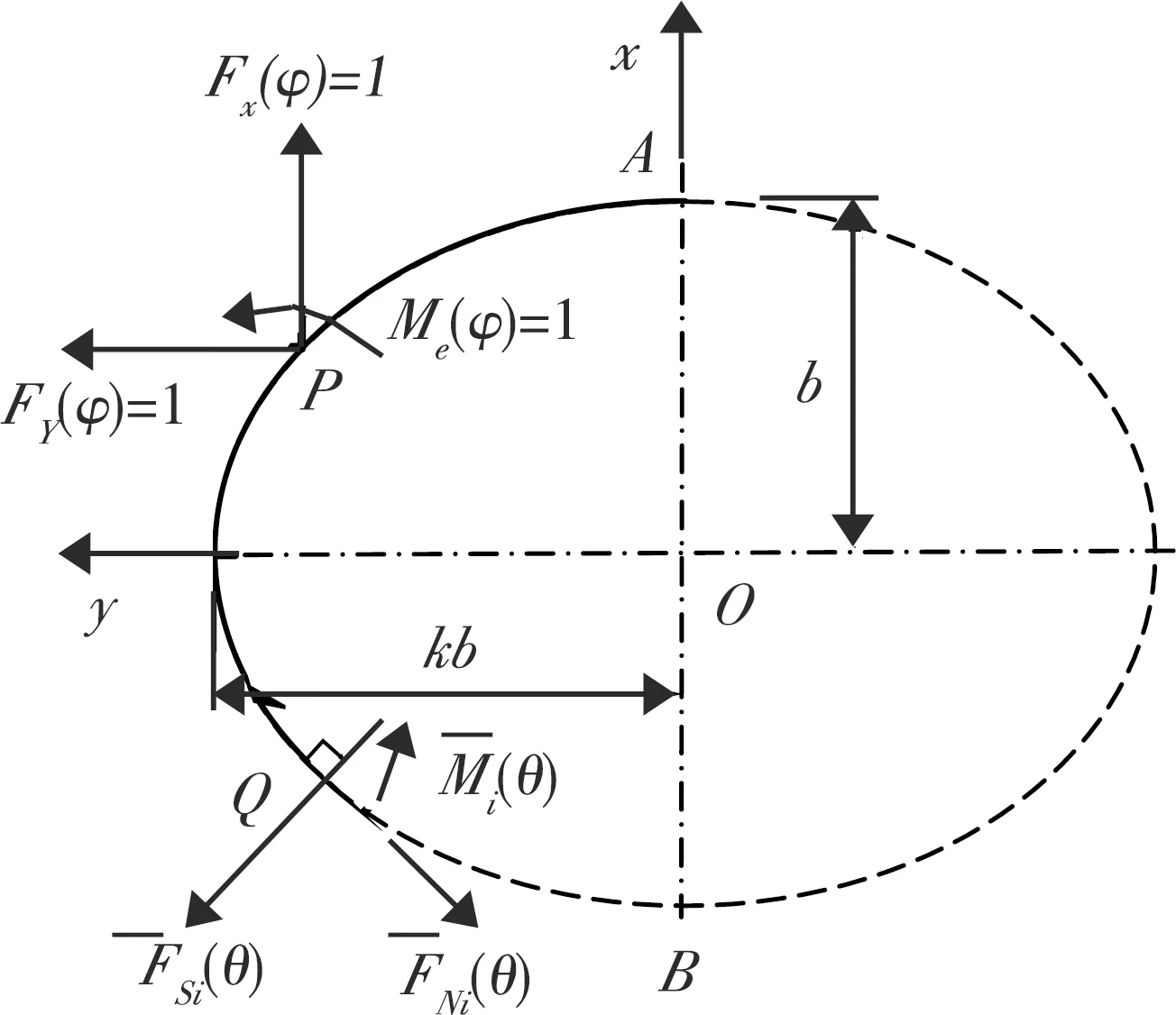
图3 单位载荷下的内力图

由单位载荷法，结合式(3)(8)(12)，计算位移：

(13)

1.2 开口椭圆环

若椭圆环在A截面开口，则据式(6)计算总内力，将式(6)代入式(13)，即可得位移。

2 算例及结果分析

令椭圆环的水平轴与铅垂轴之比为k。若k=2,借助Maple 18，由式(6)(8)可得图4所示无量纲化内力图,由式(13)可得图5所示无量纲化位移图。

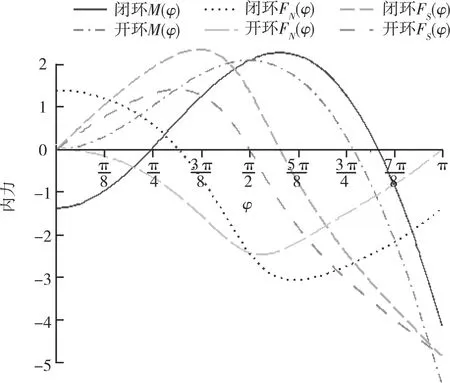
图4 k=2时无量纲化内力图

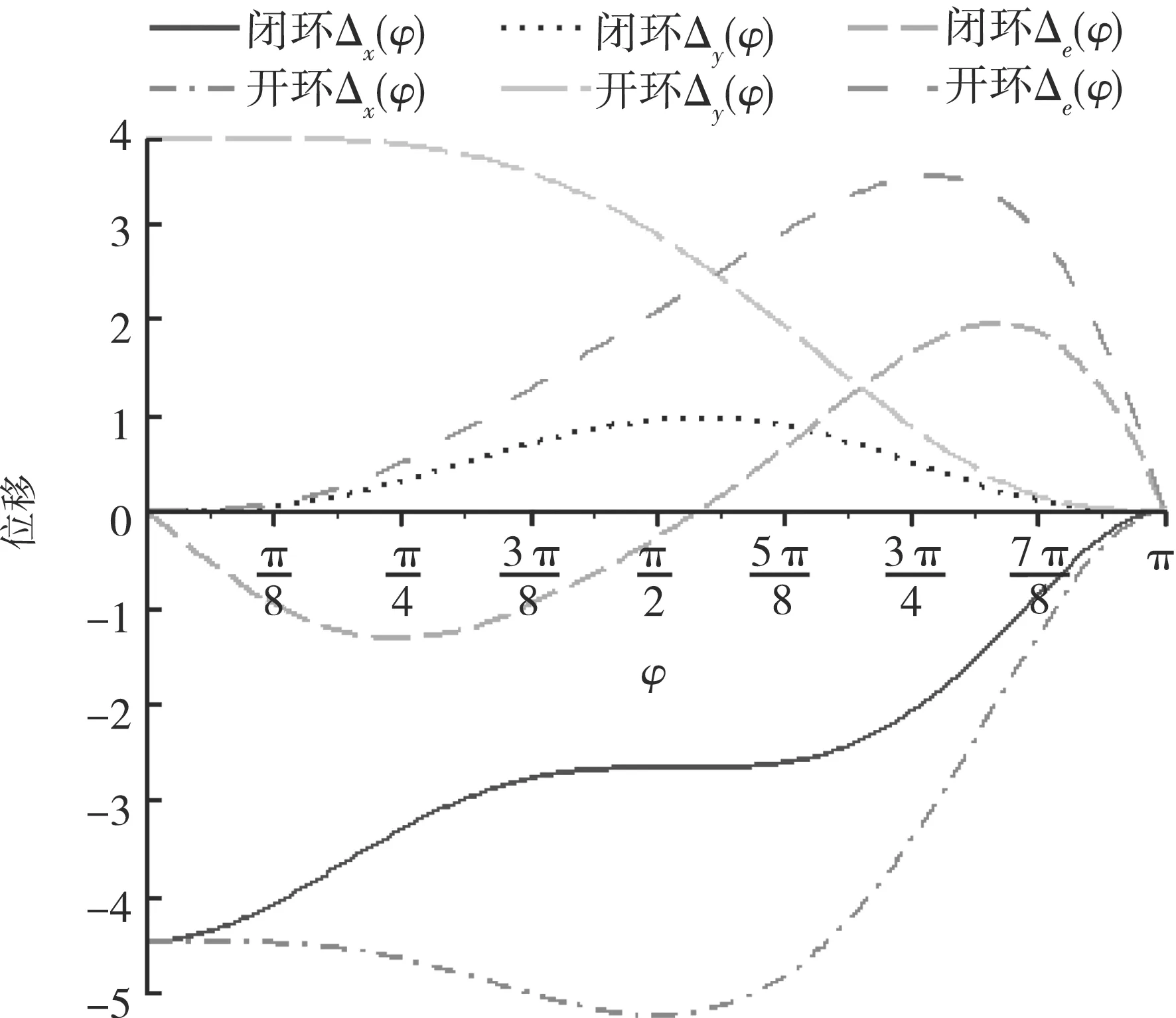
图5 k=2时无量纲化位移图

根据表1和表2所示内力和位移分析，得出以下主要分析结果。

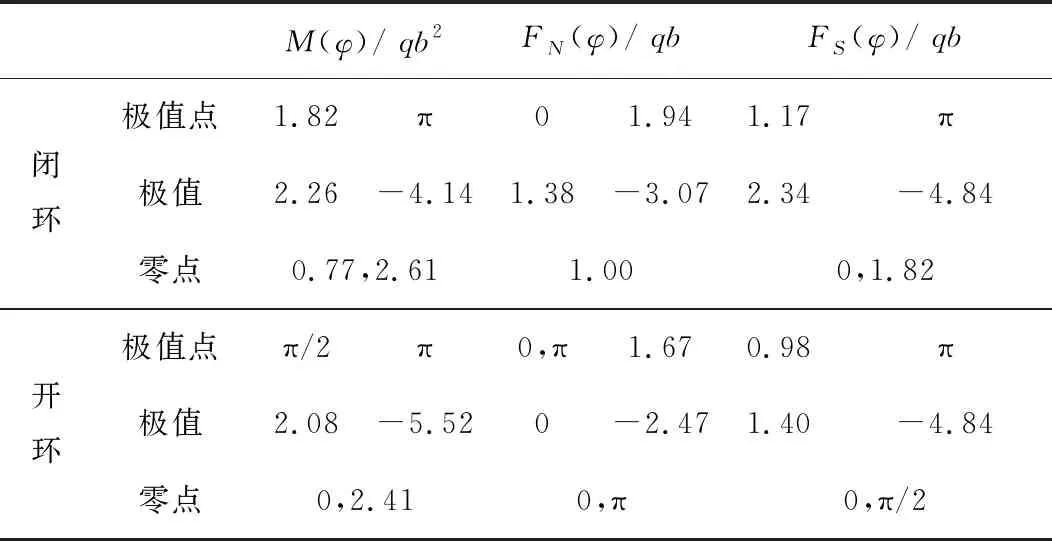
表1 k=2时的内力分析

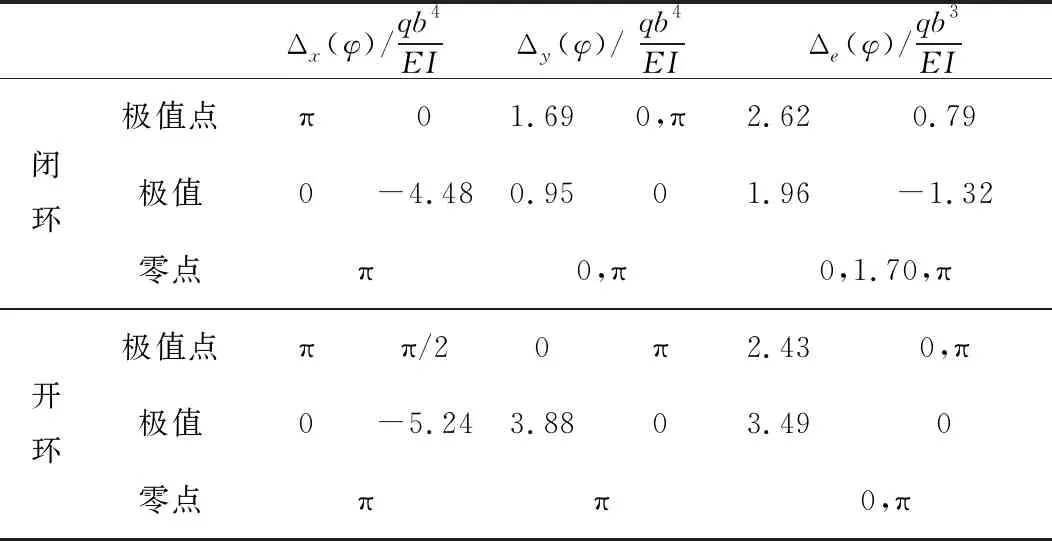
表2 k=2时的位移分析

(1) 和开环相比，闭环的弯矩极值较小，但轴力极值较大，二者在底部可取得相同的剪力极值。在水平轴上，二者的弯矩相同，轴力也相同。

(2) 闭环的3个位移极值均小于开环。沿铅垂轴的位移方面，闭环和开环在顶部相同，且闭环在该处取得极值，开环在水平轴上取得极值；沿水平轴的位移方面，开环在顶部取得极值；角位移方面，二者在顶部的转角均为0。

由于没有考虑轴力和剪力对位移的影响,故计算结果略小于实际值。