时间分数阶扩散方程的二阶差分/拟小波法
2019-05-24赵凤群
郭 冲, 赵凤群
(西安理工大学 理学院, 陕西 西安 710054)
0 引言
近年来,时间分数阶微分方程受到了广大学者的关注,它的应用领域也越来越广泛,如动力系统中的控制理论[1]、粘弹性材料[2]、混沌[3]、神经细胞中离子的反常扩散过程[4]等.
时间分数阶扩散方程是对传统整数阶扩散方程的推广,但是由于分数阶导数的存在,这类方程的求解出现了一些困难.在实际问题中,对方程建立有效的数值逼近格式是必要的.时间分数阶导数有两种直接的离散公式:L1离散公式和Grünwald-Letnikov离散公式,前者是对Caputo分数阶导数关于被积函数进行分段线性插值得到的,而后者通常用来离散Riemann-Liouville分数阶导数.
然而,上述方法的精度有限.近年来,国内外学者提出了许多数值方法,比如有限差分法、谱方法、有限元法等.Sun和Wu[5]通过引入两个新变量将原始方程转换为低阶方程组来得到时间分数阶导数的差分格式,并证明差分格式是唯一可解的、无条件稳定的和收敛的,其收敛阶为O(τ3-α+h2) (1<α<2),其中τ是时间步长,h是空间步长.Li等[6]提出了两种用于数值求解时间分数径向扩散方程的隐式有限差分格式,并证明了这两种格式是无条件稳定和二阶收敛的.Ercilia和Li[7]研究了具有Riemann-Liouville分数阶导数的一维分数阶扩散模型,并给出了该导数的二阶离散化,推导出了无条件稳定的加权平均有限差分方法.
Lin和Xu[8]提出了时间分数扩散方程的有限差分方法,并证明收敛阶为O(τ2-α).Alikhanov[9]提出了一种新的Caputo分数阶导数的差分离散公式,并建立了相应的空间四阶和二阶的有限差分格式.Chen等[10]考虑了半无限空间域上具有变系数的时间分数扩散方程的数值近似,提出了一种基于时间和频谱近似的有限差分方法的全离散格式.拟小波法与小波法相比,具有更好的局部特征,在处理复杂的几何边界条件时,拟小波方法通过选择合适的参数控制整体精度并具有良好的稳定性,而且对有局域急剧变化的非线性偏微分方程的数值求解是非常有利的.Zhang等[11]、Yang等[12]在求分数阶偏微分方程时都采用了拟小波法离散空间导数,形成了有效的数值方法.Luo等[13]运用拟小波法求解了无界空间域上Volterra积分微分方程,并给出了一些数值算例来说明此方法的有效性.
本文将L2-1σ差分公式和拟小波法应用于如下时间分数阶扩散方程:
q(x,t)u(x,t)=f(x,t),
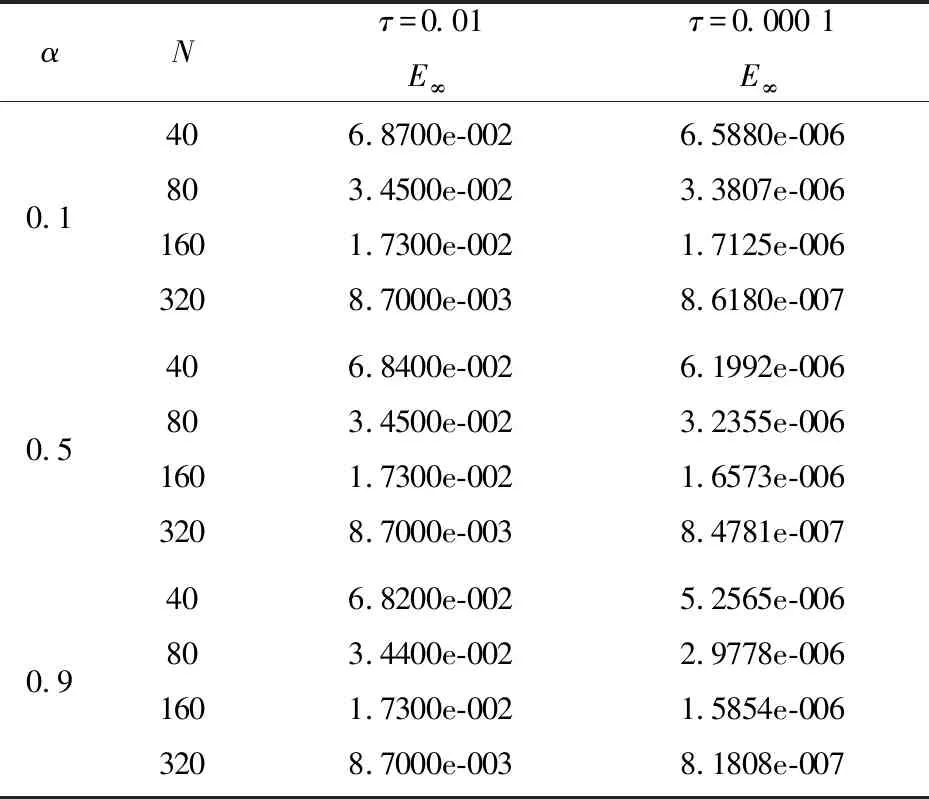
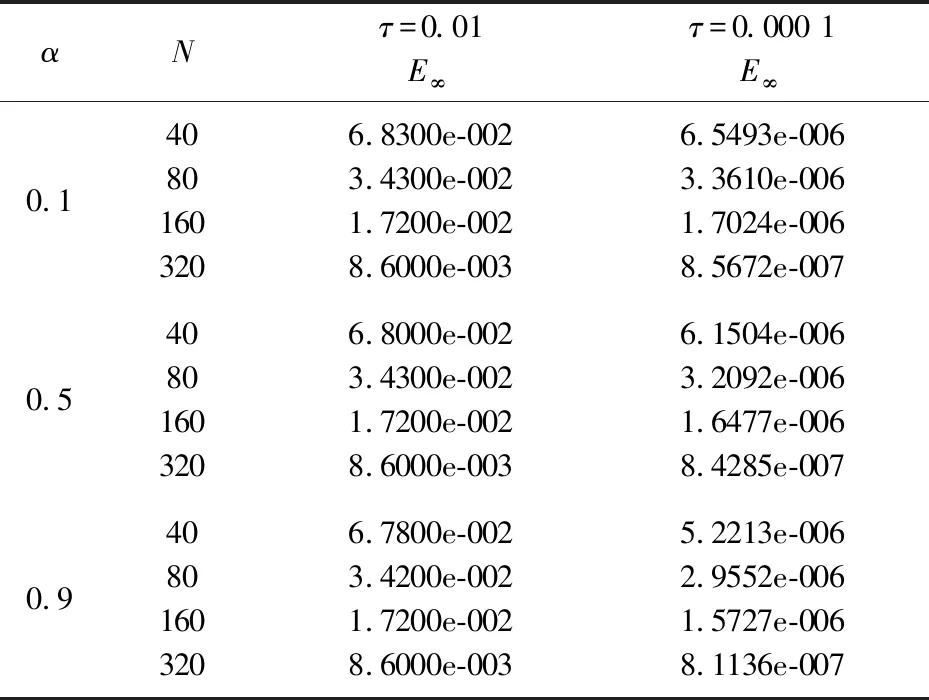
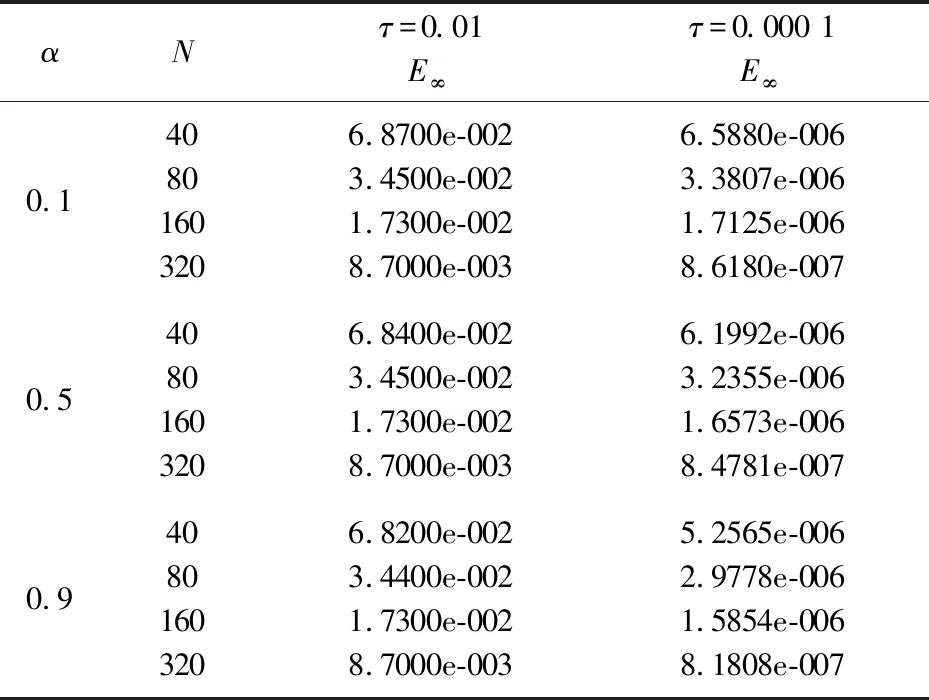
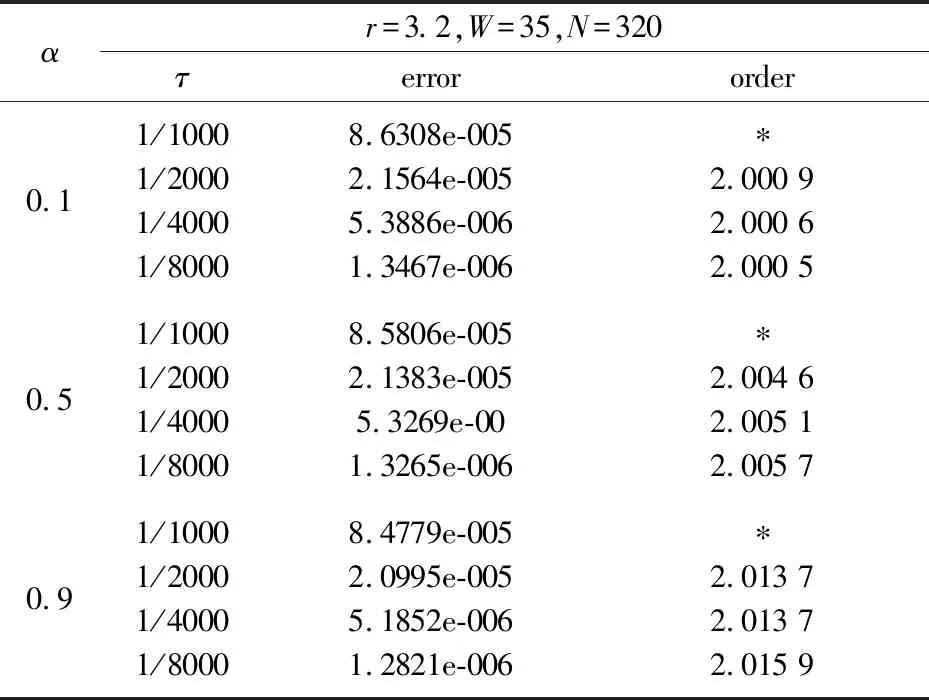
0 (1) u(x,0)=0,0≤x≤L, (2) u(0,t)=0,u(L,t)=0,0≤t≤T, (3) 其中 0<α<1是关于t的α阶Caputo分数阶导数;p≥c0>0,q≥c1>0;f是足够光滑的函数. 对于函数u(t)∈C3[0,T],考虑一致网格 文献[9]给出了Caputo分数阶导数逼近的L2-1σ差分公式 (4) 其中 ut,s=(u(ts+1)-u(ts))/τ, 当n≥1时, 引理1[9]对所有α∈(0,1)和u(t)∈C3[0,tn+1](0≤n≤M-1), 由L2-1σ公式(4),方程(1)可写成如下形式 (5) fn+σ(x). (6) 在非整数节点n+σ处,取 un+σ(x)≈σun+1(x)+(1-σ)un(x), 则半离散格式(6)可以写成 qn+σ(x)[σun+1(x)+(1-σ)un(x)]= fn+σ(x). (7) 根据引理2和引理3,有以下推论. 推论1[10]对于n=0,1,2…,M-1,具有以下不等式 根据参考文献[10],运用上述引理和推论,得到了时间半离散格式(7)的稳定性和收敛性. 定理1格式(7)是稳定的,并且对所有的τ>0,满足 ‖un+1‖2≤ 其中n=0,1,…,M-1. (10) 应用pn+σ≥c0>0,qn+σ≥c1>0和推论1,得到 (11) 用Hölder不等式与young不等式,得到 不等式(11)就可以写成 即 ①当0<α<1时, 由于 所以 (12) 当n=0时,由式(12)得到 显然不等式(8)成立. 假设当n ‖un+1‖2≤‖u0‖2+ 则当n=k时, 于是有 ‖uk+1‖2≤‖u0‖2+ ②当α→1时 由于 所以 (13) 当n=0时,由式(13)得到 显然不等式(9)成立. 假设当n 则当n=k时, 于是有 从而定理1的不等式(9)得证. 2.3.2 慢性肾功能不全(CKD):CKD影响血小板聚集能力和凝血功能,CKD患者肾脏排泄能力减低又会影响抗血小板药物代谢。因此,CKD患者既是血栓高危人群也是出血高危人群,在应用抗血小板药物前必须进行肾功能评估和出血风险评估。目前更倾向于替格瑞洛联合阿司匹林,PLATO研究亚组分析[10]显示,CKD 患者在阿司匹林治疗的基础上,替格瑞洛较氯吡格雷治疗组主要心血管复合终点事件及全因死亡率降低更明显,且严重出血事件风险未增加。 类似定理1,可以证明: ‖u(tn)-un‖2≤ 拟小波法主要是通过以下插值基函数来配置[11] 其中σ是正则宽度参数,Δ是单元网格大小,选取σ=rΔ,r是计算中选择的参数. 对于时间半离散格式(7),空间上采用拟小波法,给出如下网格xj=jh,j=0,1,…,N,h=L/N,时间步长记为τ,tn=nτ,n=0,1,…,M. 假设 (14) 则nu(x)在xj点的n阶求导格式为 令p-j=m,则 (15) 将式(15)代入格式(7)得其离散格式为 (16) 式(16)即是时间分数扩散方程(1)的拟小波法的全离散格式,且该格式在空间上是指数收敛的[14]. 求解如下时间分数阶扩散方程 (17) 满足如下初边值条件 u(x,0)=0,0≤x≤1, u(0,t)=0,u(1,t)=0,0≤t≤1. 其中 精确解为u(x,t)=t2sin(πx). 此方程的数值结果呈现在表1~4.表1、表2和表3分别给出了M=100,参数r和W取不同值时,随着α的改变,在不同时间和不同空间步长下的最大模误差.其中最大模误差E∞定义为 从表1、表2和表3可以看出,当W保持不变时,随着r的增大,误差也在变大.当r保持不变时,随着W的增大,误差保持不变. 表4显示了随着时间步长τ的变化,通过上述算法求得的误差.从表4可以看出,该算法的收敛阶为O(τ2),这也验证了理论分析的正确性. 表1 r=3.2,W=35,M=100,N取不同值时的误差分析 表2 r=2.2,W=35,M=100,N取不同值时的误差分析 表3 r=3.2,W=20,M=100,N取不同值时的误差分析 表4 τ取不同值的误差分析 本文给出了基于L2-1σ公式的时间分数阶扩散方程的半离散格式,并得到了它的稳定性和收敛性.采用拟小波法离散空间导数,从而建立时间分数阶扩散方程的全离散格式.本文算法在空间上具有指数收敛的特点,在时间变量上收敛速度也较高,是一种高效的数值方法.1 基于L2-1σ差分公式的时间半离散格式
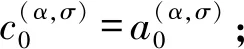
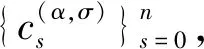
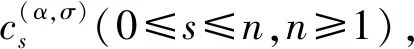
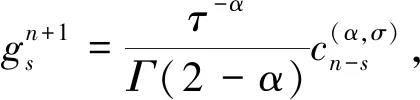

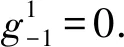
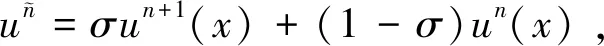
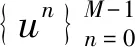
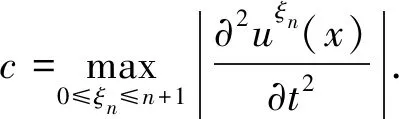
2 全离散拟小波格式
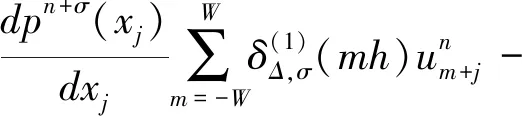
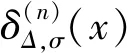
3 数值算例
4 结论
