芦苇不同铺放状态下可压缩性分析

朱海燕，张立新，葛 云，李继霞，陈可圣，王 欢

(石河子大学 机械电气工程学院，新疆 石河子 832000)

0 引言

作为目前造纸工业的重要原料的芦苇，具有“第二森林”的美称，其用途广泛，最重要的还是上佳的环保材料。芦苇成本低廉，自身松散，但其较高的运输成本和囤积费用严重影响了造纸企业的利润[1]。因此，进行芦苇高密度打捆的研究对于是提升芦苇运输效益和囤积效益具有重要意义。

国内外对芦苇高密度打捆的研究已经取得了一定进展。1938年起，国外学者率先采用闭室压缩的试验方法对物料包的压缩性能进行了研究[2-5]，得到了许多草物料压缩的经验公式。国内对于粗纤维草物料压缩的性能研究起步晚于国外。吕江南[6-7]等对不同粗纤维物料进行压缩特性研究，建立了不同粗纤维物料压力及压缩密度的数学模型。王春光、范林[8-9]等对于压缩室中草物料的高密度压缩时的受力状况、变形程度进行了分析研究。李旭英、杨明韶[10]等对压缩过程中的截面积、喂入量、含水率、压缩频率等影响因素进行了试验分析。这类基础性研究为粗纤维草物料的流变学理论的深入研究及打包机的结构设计提供了理论基础。粗纤维物料的可压缩程度反映了物料抵抗外力时产生形变的能力大小[11]。传统压缩方式中，粉碎后芦苇处于自然堆积、无序布置的杂乱状态，直接压缩作用。关于草物料不同压缩状态下的特性，尚未进行深入的研究。为此，本试验对芦苇在轴向、径向及杂乱压缩状态进行闭式压缩试验，为芦苇高密度压缩机理分析及打捆机喂入装置优化设计提供了理论依据。

1 材料与方法

1.1 试验材料

本试验采用阿勒泰芦苇(不包括穗头)为样品，平均长度150mm，干燥环境下自然风干1个月。先使用电热鼓风干燥箱进行烘干处理后称烘干后质量m1，根据公式(1)进行配水试验，按照所需含水率均匀喷洒水m2，放入密封袋标记后静置48h，则

(1)

其中，α为湿基含水率；m1为烘干后芦苇质量；m2为水的质量。

1.2 试验装置与仪器设备

为进行芦苇不同压缩状态的研究，采用如图1的压缩装置，主要由活塞杆、压缩盖板及压缩箱组成。压缩装置均采用5mm厚的45钢，压缩箱体内截面尺寸250mm×250mm，活塞杆高度150mm，压缩盖板增加4个肋板，箱体四周加装4组三角铁，压缩箱体内部标有4组刻度尺，方便试验记录。

压缩测试系统如图2所示。试验使用的仪器设备有ACS系列电子秤、电热鼓风干燥箱、游标卡尺及CSS44000系列微机控制电子万能材料试验机。根据试验要求，配套使用EDC120数字控制器、GWB-200型高精度位移标定器及引伸计等。

图1 压缩模具

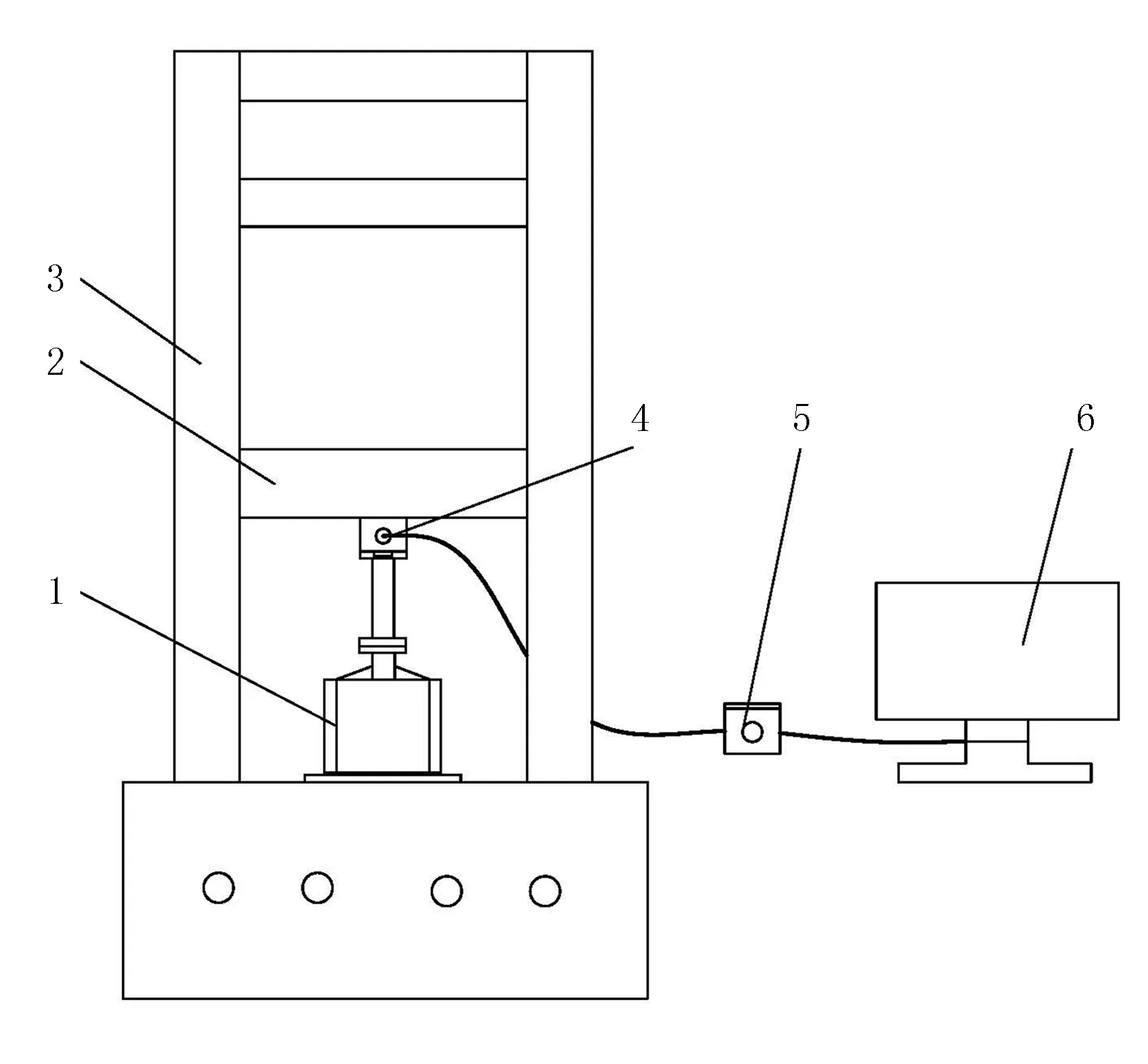
1.压缩模具 2.试验机升降台 3.万能试验仪机架 4.压力传感器 5.数据采集仪 6.计算机

1.3 试验因素确定

通过前期的资料文献查阅及试验发现：在打包压缩过程中芦苇杆的粉碎主要受到径向压缩力、轴向压缩力及带有不同倾斜角度的压缩力的影响。为确定芦苇径向[12](芦苇杆在压缩箱体内呈横向的铺放状态)、轴向(芦苇杆在压缩箱体内呈竖向的铺放状态)和杂乱状态(芦苇杆在压缩箱体中呈横竖杂乱交错状态)压缩对压缩密度的影响，经过预试验，确定本研究芦苇的最终压缩密度为259kg/m3，喂入量为900g，压缩速度10mm/min，含水率分别为13%、15%、17%，进一步深入分析芦苇在竖直、平铺与杂乱3种铺放状态下，压缩至相同密度时压缩力、压缩密度、压缩时间、体积模量之间的变化关系。体积模量表示材料在受均压下体积缩小的难易程度，体积模量越大，表明物料的抗压能越强。

压缩密度计算公式为

(2)

体积模量计算公式为

(3)

其中，K为体积模量(MPa)；l为芦苇高度(mm)；F为压缩力(N)；p为压应力(N/m2)；S为箱体面积(mm2)。

2 芦苇不同铺放状态下压缩试验结果

根据试验方案进行试验后，对试验数据整理分析，可得到芦苇在可得到芦苇在轴向压缩、径向压缩及杂乱压缩3种压缩状态下压缩力、活塞位移及芦苇高度等数据。将数据带入公式(2)和公式(3)中，可得到芦苇在这3种状态下的压缩力、压缩密度、压缩时间及体积模量的数值变化关系，如图3所示。芦苇的压缩性能即在压力作用下体积缩小的特性，体积模量反映材料在受力作用下抗压缩能力的大小。

芦苇含水率为13%、15%、17%时，竖直、平铺和杂乱3种压缩状态下压缩力与压缩密度的关系如图3～图5所示。轴向压缩时，由于芦苇长度存在差异，每个芦苇杆受力大小不均匀，芦苇为空心薄壁结构，芦苇的轴向强度比径向强度大，压缩过程中压缩盖板出现倾斜，无法压缩成型，后续不进行对比分析。图6～图8对比了13%、15%、17%不同含水率下芦苇在杂乱和平铺两种状态时压缩密度与体积模量的关系。

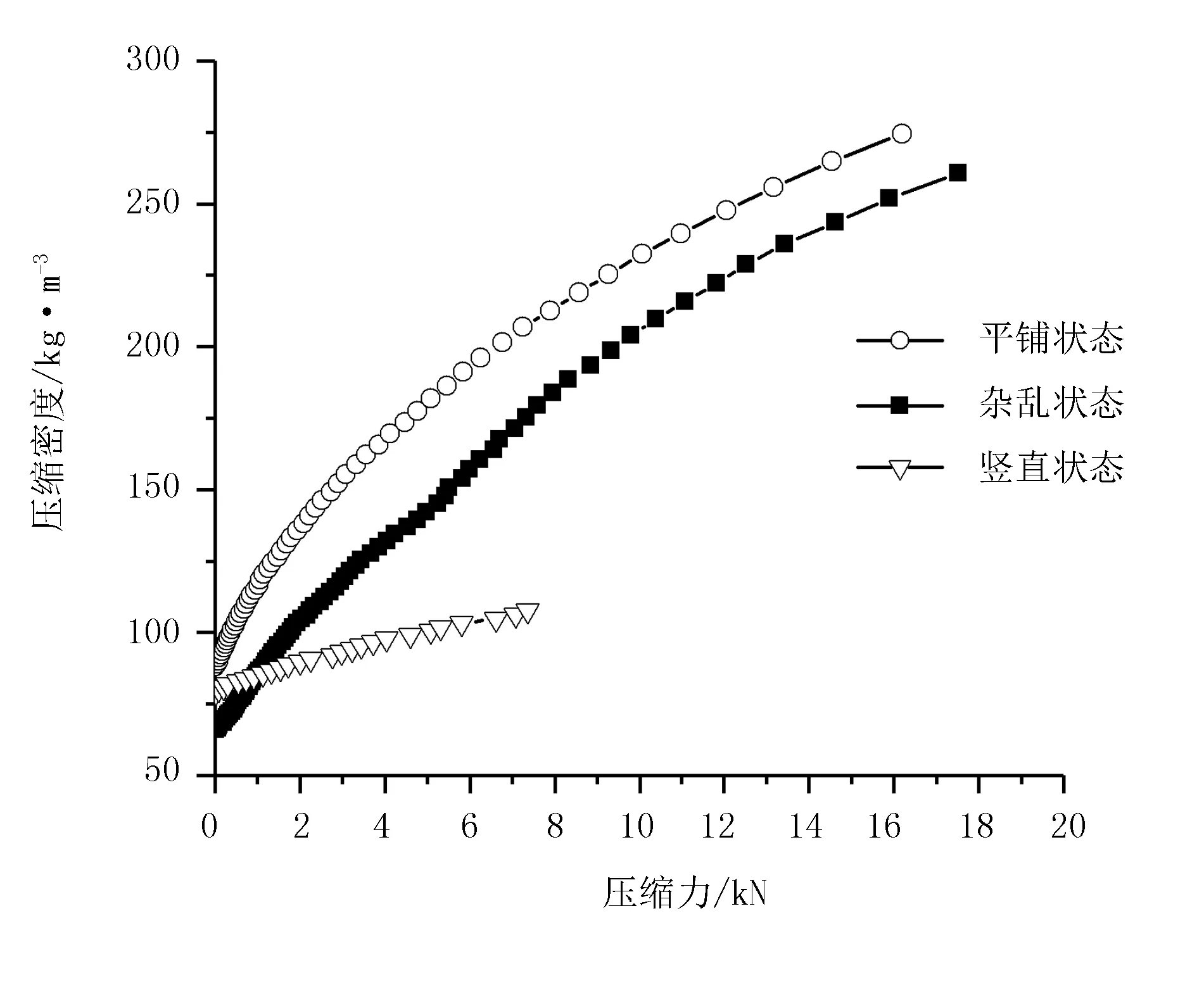
图3 13%含水率下3种压缩状态压缩力与压缩密度的关系

图4 15%含水率下3种压缩状态压缩力与压缩密度的关系

图5 17%含水率下三种压缩状态压缩力与压缩密度的关系

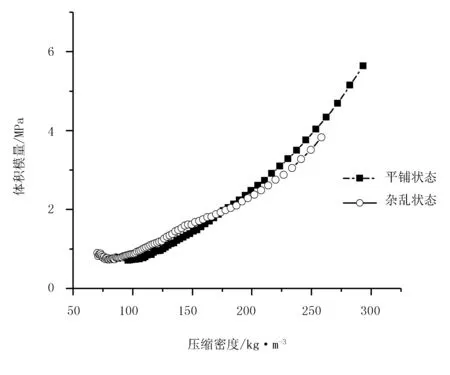
图6 13%含水率下两种压缩状态下压缩密度与体积模量的关系

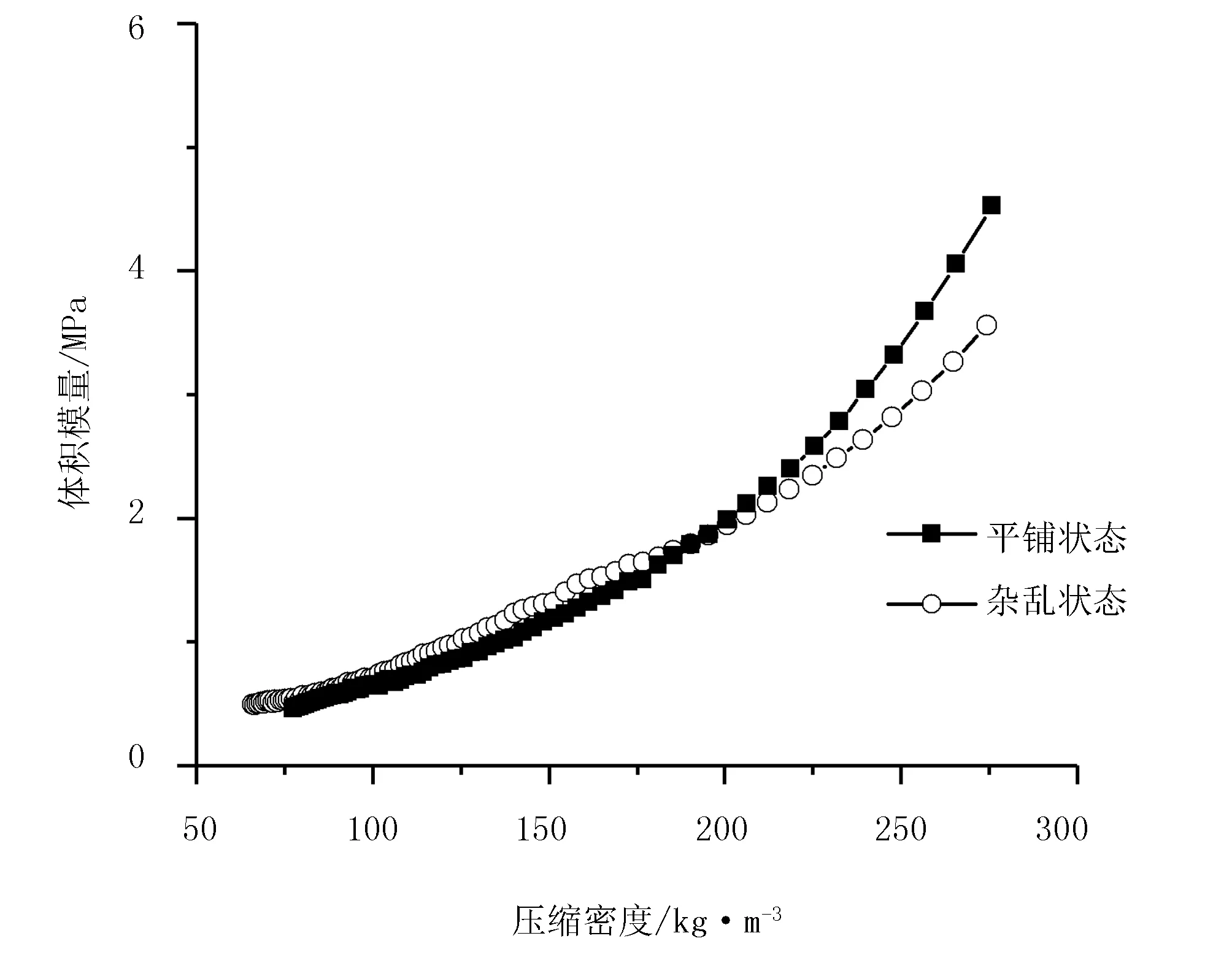
图7 15%含水率下两种压缩状态下压缩密度与体积模量的关系

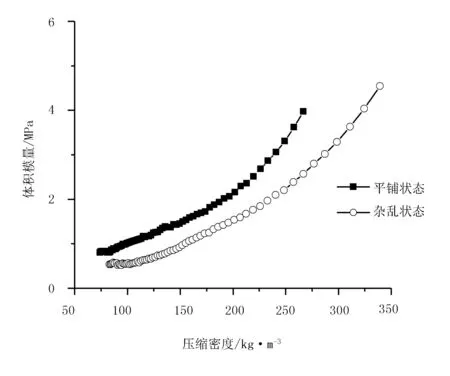
图8 17%含水率下两种压缩状态下压缩密度与体积模量的关系

由图3～图8可以看出：不同含水率下芦苇压缩变化的趋势相似，压缩密度随着压缩力的增加而增大，体积模量随着压缩密度的增大而增大。由图3～图5可以看出：压缩密度随着压缩力的增加而增大；初始阶段，随着压缩力的增加，芦苇的密度快速增加，在较小的压力作用下芦苇密度迅速增加，芦苇的可压缩性较好。对应图6～图8的初始阶段，芦苇体积模量较小，且增加速度比较缓慢，芦苇抵抗变形的能力较弱，将此阶段定义为松散阶段。此阶段主要是缩小芦苇间的空隙，使芦苇紧密接触；随着压力的增加，芦苇密度的增加速度开始有所降低，进入图3～图5的中间阶段，芦苇的可压缩性开始变差。对应图6～图8的中间阶段，芦苇体积模量增加速度加快，芦苇抵抗变形的能力增大，将此阶段定义为芦苇破碎阶段。此阶段由于压力的增加紧密接触的芦苇开始因相互挤压而产生破裂，进一步使芦苇更加紧密的接触在一起。随着压力的继续增加芦苇密度的增加较为缓慢，进入图3～图5的最后阶段，芦苇的可压缩性最差。对应图6～图8的最后阶段，芦苇体积模量增急剧增加，芦苇抵抗变形的能力也急剧增加，将此阶段定义为压实阶段。此阶段紧密接触并且破碎的芦苇开始逐步接近致密、均匀的固体，同时对侧壁的正压力增加，与箱体的摩擦力逐步增加，再继续增加压缩力，密度增量更为缓慢。

由图3～图5对比杂乱和平铺两种压缩状态可以发现：平铺状态的初始压缩密度均大于杂乱状态下的初始压缩密度。原因可能是：在平铺压缩方式下的松散阶段，芦苇间的空隙较小，克服空隙变形所需的力及时间少于杂乱压缩状态。图6～图8中：在初始阶段，平铺状态的曲线切线斜率大于杂乱状态的，表示平铺状态的体积模量增速快，平铺状态在初始阶段抗压缩性大。

芦苇含水率为13%、15%、17%时，平铺、杂乱两种状态下压缩密度与压缩时间的关系如图9～图11所示。3幅图曲线变化趋势相似，平铺状态下的曲线斜率均大于杂乱状态下的斜率。这表明，在平铺状态下的压缩速率高，达到较高压缩密度所需的时间小于杂乱状态下。

图3～图5、图9～图11数据总结如表1表示。当质量相同的芦苇压缩成型并达到259kg/m3的压缩密度时，在平铺压缩状态下需要的最大压缩力均小于杂乱状态的最大压缩力，相应的压缩时间也减少15%～33%，提高了压缩效率及压缩质量。

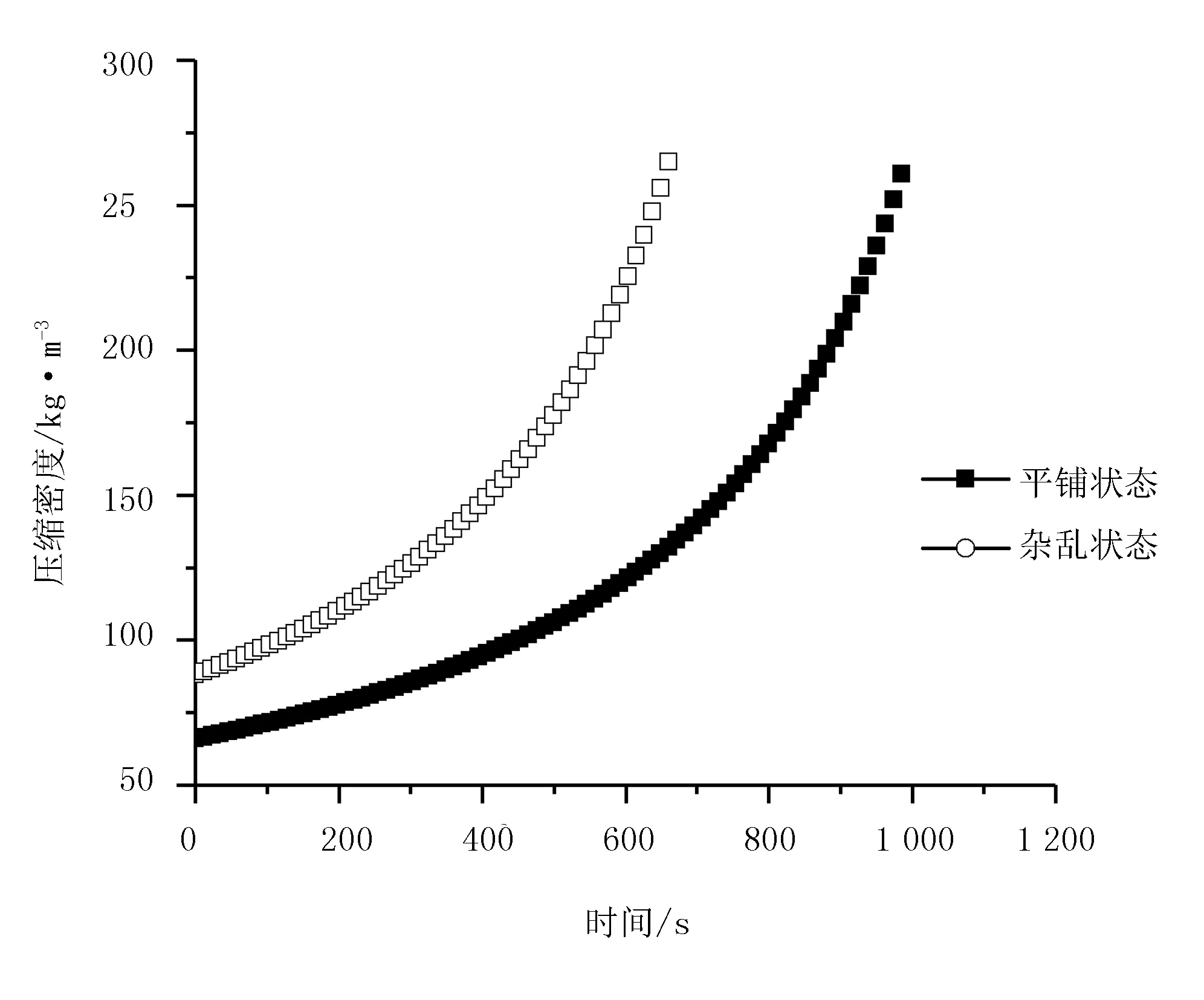
图9 13%含水率下压缩密度和压缩时间的关系

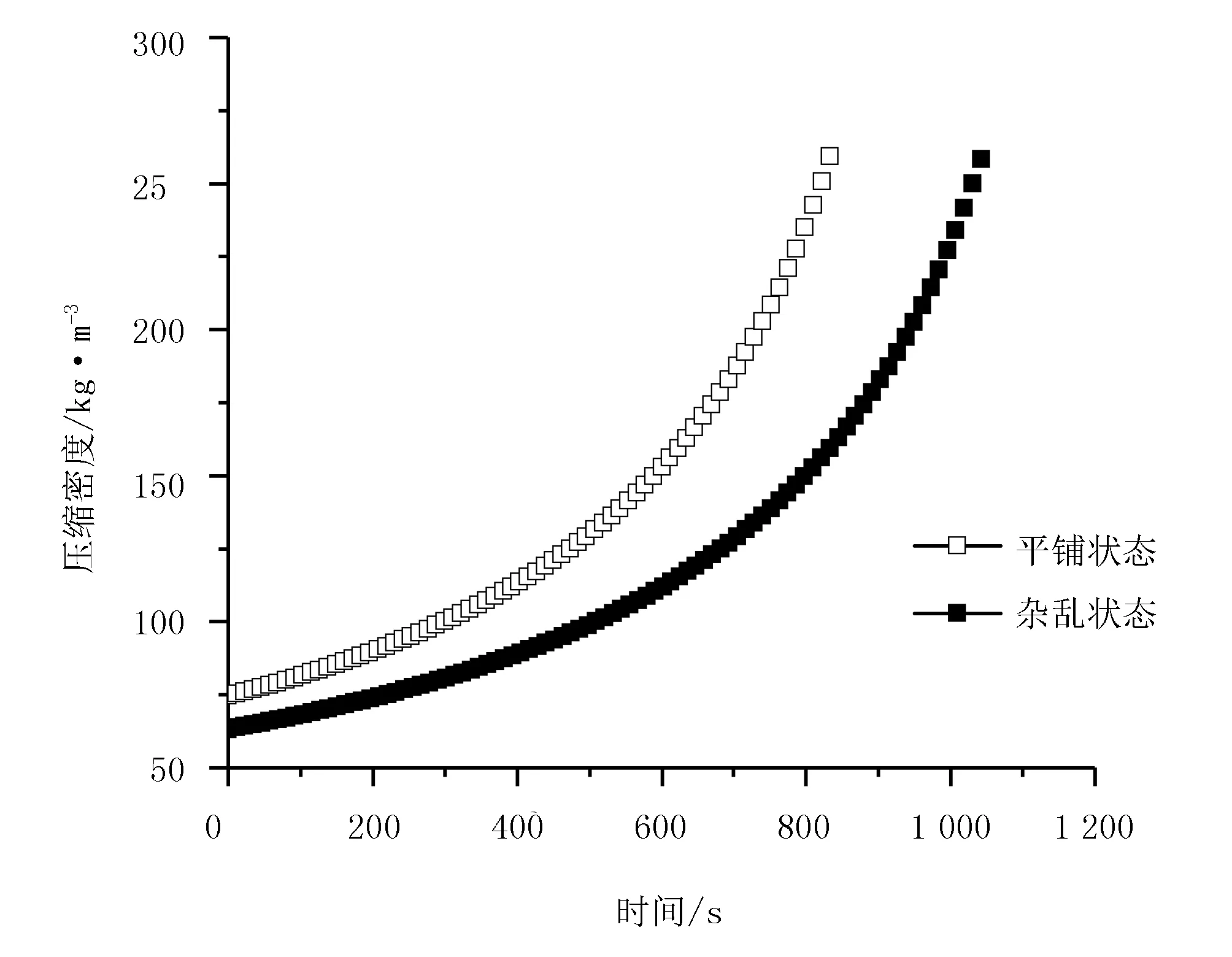
图10 15%含水率下压缩密度和压缩时间的关系

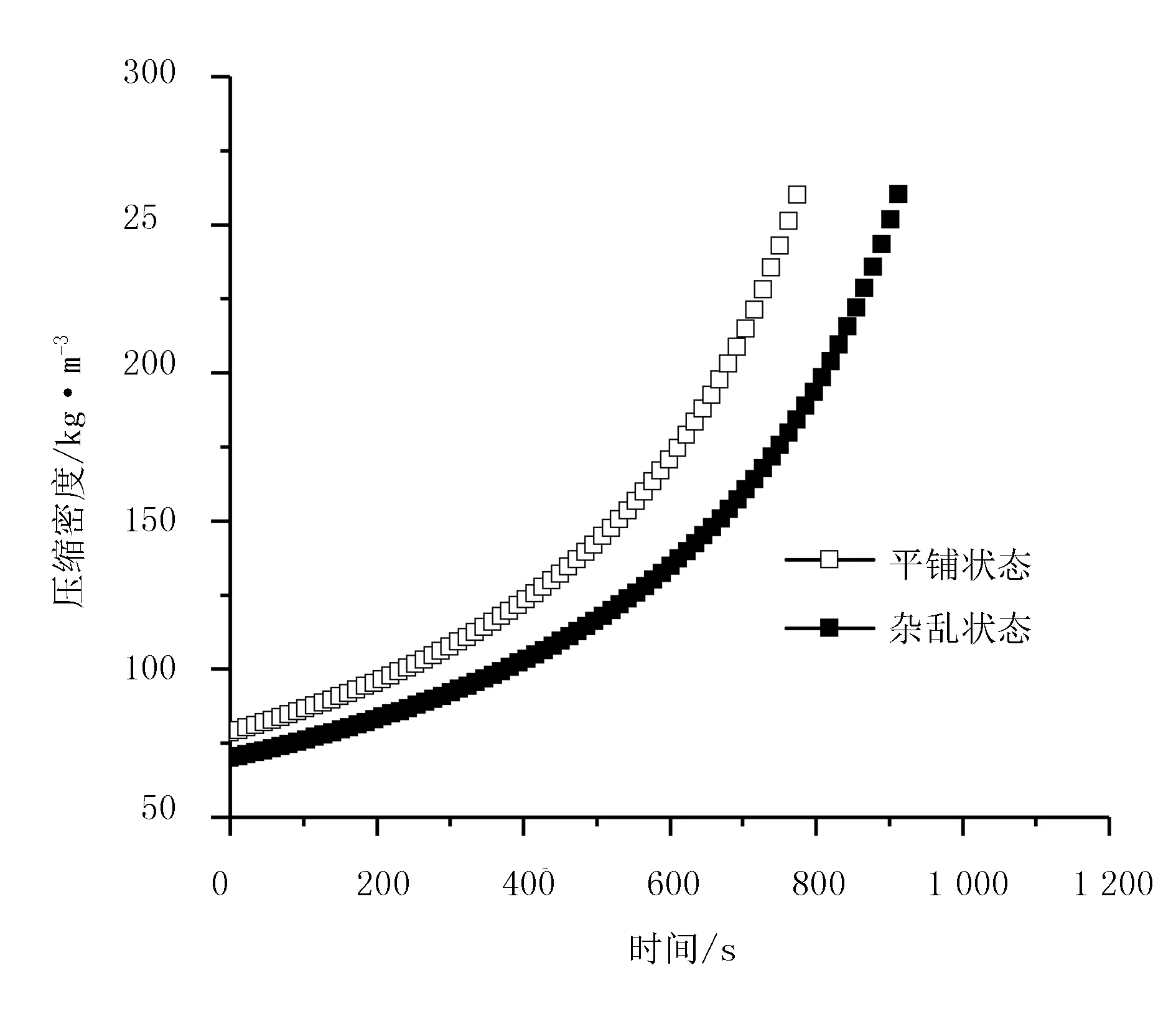
图11 17%含水率下压缩密度和压缩时间的关系

表1 不同含水率在杂乱、平铺状态下的最大压缩力及压缩时间

Table 1 Comparison of maximum compressive force and compression time of different water content in messy and tiling conditions

含水率/%压缩状态压缩密度/kg·m-3最大压缩力/kN13 杂乱259 17.582 13 平铺259 13.96915 杂乱259 15.09615 平铺259 14.50117 杂乱259 15.47817 平铺2598.568

3 体积模量与压缩密度的数学模型

对图6～图8中13%、15%、17%含水率时两种压缩状态下压缩密度与体积模量的试验数据进行回归分析，结果如表2所示。

表2 不同含水率在杂乱、平铺状态下的压缩密度与体积模量回归分析

Table 2 Regression analysis of compression density and bulk modulus of different water content in disordered and tiled state

含水率/%压缩状态拟合方程相关系数R213杂乱K=0.79e ρ/152.747-0.5710.99013平铺K=0.830e ρ/141.388-0.9580.99815杂乱K=0.909e ρ/176.583-0.8380.99315平铺K=1.018e ρ/186.192-0.9950.99717杂乱K=0.315e ρ/108.703-0.2020.99717平铺K=0.448e ρ/142.355-0.3370.998

由回归分析结果可以看出：不同含水率时杂乱、平铺状态下的非线性拟合相关系数R2接近1，具备显著性。

综上所述，芦苇在杂乱、平铺状态下体积模量与压缩密度关系指数曲线模型为

(4)

其中，K为体积模量；a、b、c为拟合系数；ρ为压缩密度。

4 结论

1)芦苇压缩过程可分为3个阶段，即松弛阶段、芦苇破碎阶段和压紧阶段。松弛阶段压缩力与压缩密度成线性增长的关系，芦苇破碎阶段呈指数增长的关系，压紧阶段芦苇的压缩力与压缩密度呈缓慢增长的线性关系，趋于平缓。

2)在芦苇秸秆的品种、加载速度、压缩室形状及质量等都确定的前提下，竖直状态压缩芦苇由于长度差异、受力不均，芦苇为空心薄壁结构，因此轴向强度比径向强度大，压缩过程中压缩盖板出现倾斜，无法压缩成型，不成型；当达到相同的压缩密度259 kg/m3时，芦苇在平铺状态下所需的最大压缩力及压缩时间均小于在杂乱铺放状态；芦苇轴向、径向力学差异性明显，在压缩过程中较理想加载方向是芦苇的径向方向，与加载方向相同径向分布的芦苇数目越多、压缩过程能耗越多，压实效果越好，致密成型的芦苇包质量越稳定。

3)芦苇在杂乱、平铺状态下体积模量与压缩密度的关系呈指数趋势增长，同时得到了芦苇在杂乱、平铺状态下体积模量与压缩密度的数学模型。