基于Hyperworks的油箱支架综合设计优化
2019-05-24王志方梁会会丁有治
吕 川,王志方,梁会会,张 强,丁有治
(万丰控股集团有限公司中央研究院)
油箱与燃油的重量主要依靠于支架的支撑,一旦油箱支架遭到损坏,很容易导致后果严重的交通事故。因此,在支架的设计阶段,要充分考虑其在汽车不同行驶工况下的受载情况,确保整个支架的载荷大小低于材料本身的强度极限。
Optistruct通过在给定的连续设计区域中找到最佳材料分布形式,进行拓扑优化从而在相应约束下满足目标设计变量的设计要求。在此过程中可以更直观地理解结构内部的负载的工作部分和传输路径,并且便于产品的整体结构形式设计从而使用更少的材料,降低设计成本。本文综合考虑了制动,转向和垂直冲击条件下油箱支架的载荷情况,在Hyperworks中采用材料插值的结构拓扑优化方法,得到优化的支架结构,满足几种常见工况下的强度要求。
1 优化设计的数学基础
优化设计基于最优化理论,其三要素分别是设计变量,目标函数和约束。设计变量是一组在优化过程中发生变化的参数,以提高性能。目标函数是需要最佳设计性能并且与设计变量有关的函数。约束是设计约束,是设计变量和其他性能的要求,其基本构成如下所示。
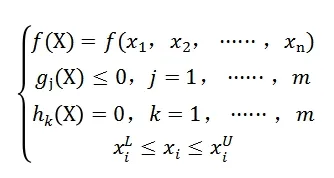
其中X=(x1,x2,......,xn)是设计变量,f(X)是目标函数,g(X)是不等式约束函数,h(X)是等式约束函数;为设计变量下限,为设计变量上限。在OptiStruct中,目标函数f(X)、约束函数g(X)与h(X)是从有限元分析中获得的结构响应。
拓扑优化在解决结构刚度最大化问题时,通常是转化为柔度最小问题来研究,这样就可以用定义柔度的变量来间接地衡量刚度,其数学表达式可以表示为:
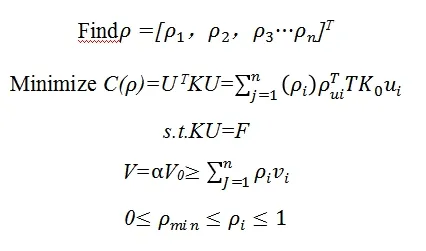
2 油箱支架设计与工况
在考虑油箱,支架,纵梁,垫板和紧固带之间作用关系的情况下,使用合理的结构来模拟它们之间的接触力传递以建立相关模型。该模型采用一阶四边形和三角形单元,基于模型的整体几何尺寸和结构特征,单元的平均尺寸定义为5 mm,油箱组件的网格参数如表1所示。

表1 油箱总成的网格参数
RBE2用于模拟油箱支架和框架之间的螺栓连接,并限制支架上螺栓孔的所有自由度;油箱和支架之间的接触以及紧固带和支架之间的接触使用GAP单元连接,如图1所示。对于油箱中的燃料质量通过RBE3单元连接到罐的内表面,保证其质量分布均匀,如图2所示。为了使模型更接近实际工作条件,所有接触部件建立group关系。油箱、固定带、橡胶垫、支架与纵梁之间分别以Interface建立主从连接,并将RBE3连接到油箱内壁单元节点,并从该点施加0.454t的满载质量。

图1 模型各部位连接
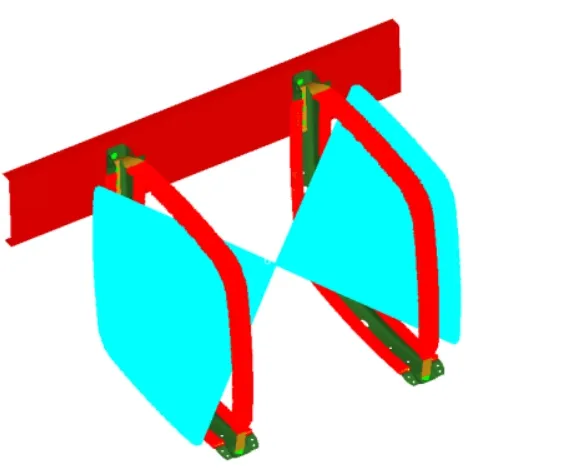
图2 油箱燃油质量
油箱的质量为52千克,支架组件的质量为12.8千克。模型相关材料和属性参数如表2所示。
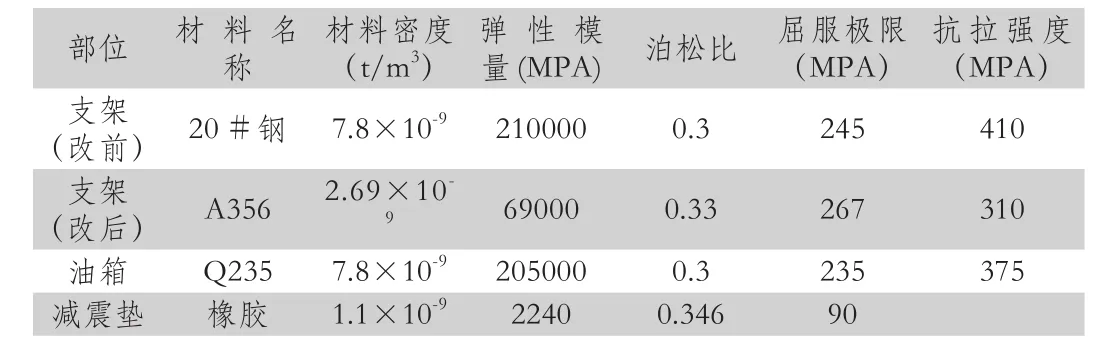
表2 模型内各零件材料参数与属性
在整车坐标系中,x,y,z是坐标系中三个方向的坐标值(正值为正,负值是反向),其中x是汽车的相反方向,y指向汽车的右侧,z指向汽车的顶部。
油箱受到的极限载荷主要有刹车、转向以及遇到颠簸路面的垂直加速度等几种工况。为保证安全性,取动载系数为1.5[4],除静载状况下在az=-1g的重力载荷外,在过坑、制动、转弯三个工况分别额外施加az=-1.5g、ax=-0.5g、ay=0.5g的加速度。
3 仿真结果与拓扑优化
将相应的加载和约束条件应用于有限元模型,并建立静态分析所需的加载步骤。在垂直冲击,制动和转向条件下,支架组件的最大应力分别为175.1 Mpa,99.5 Mpa和58.3 Mpa。
其中油箱支架的最大应力如图3所示,油箱支架的最大应力集中在与纵梁连接的螺栓孔的周围。不断增加平均支架厚度,直至在支架平均厚度为10mm时,最大应力值为175.1Mpa,考虑到1.5倍的安全系数,175.1262.25,低于屈服极限。

图3 10mm平均厚度颠簸工况下的应力分布
在hypermesh中进行支架的质量最小化设计以减轻材料,迭代直至收敛。根据图4密度云图显示,蓝色为可设计区域,可以进行拓扑优化减轻材料,红色为不可设计区域,不能减少其材料。由于改后支架不再为钣金件而是铸件,且其结构已经属于加强筋,因此可以对红色部分进行的局部厚度优化。

图4 拓扑质量优化的密度云图
在可设计区域进行镂空处理以节省材料,在保持平均厚度的情况下,加强引力较大部分的局部厚度,通过最优化设计寻求最优的平均厚度与局部厚度,如图5所示。

图5 加厚区域与镂空区域
当加厚最大应力部位的厚度时,颠簸工况所受最大应力值明显下降,因此可以重新对平均厚度和局部厚度进行寻优,计算结果如表3所示。

表3 平均厚度与局部厚度下的最大应力

图6 6mm平均厚度下局部优化设计应力分布
该形状的油箱支架模态幅值以前三阶最大,原始固有频率分别为3.953HZ,6.765HZ,16.313HZ,优化后固有频率为3.964HZ,6.767HZ,16.334HZ,如图7、图8所示,可以认为模态基本没有发生变化,不存在增加共振危险性的情况。

图7 原始一阶模态振幅

图8 优化后一阶模态振幅
4 结论
本文基于材料插值理论,分别考虑几种路况条件下的载荷影响,从而对原油罐支架进行优化计算。在保持静刚度的条件下,以质量最小的多目标拓扑优化作为目标,通过对应力云图和密度云图的研究,找到需要加强结构的区域和对荷载传递影响较小的区域。修改原始支架的厚度以获得新的支架结构,使其基本上保持原始静态性能的前提下从原本12.8 kg减重至7.7 kg,减重39.8%,大大节省了铝合金材料。
