海洋吊索碰撞动力学分析
2019-05-23张大朋朱克强
张大朋,白 勇,朱克强
(1.浙江大学 建筑工程学院,杭州 310058;2.宁波大学 海运学院,宁波 315211)
随着对海洋资源需求的日益增大,各种针对海上结构物的施工作业越来越频繁,尤其是海上起吊作业。而在海上起吊作业过程中由于各种原因导致的吊缆间的碰撞不可避免。而这种吊缆间的碰撞对海上施工作业是不利的。该过程中产生的高速反弹会对周围的设备和人员造成极大的伤害[1-4]。
目前国内关于海洋起吊方面的动态分析较多,但关于吊缆之间的碰撞研究较少。相对于单独研究海洋起吊系统,起吊吊缆间的碰撞涉及到复杂的碰撞接触之间的设置,并且在碰撞过程中极易出现缆-缆之间的相互缠绕,不能简单地依据吊缆模型建模,而直接编程工作量过于浩大,且计算过程极难收敛。吊缆的动力学建模方法有集中质量法、有限元法和有限差分法等[5-9]。其中,集中质量法物理意义明确,算法简单易懂,具有广泛的适用性及扩展性。本文以大型水动力分析软件OrcaFlex 软件为平台,运用凝集质量参数法建立了吊缆碰撞的动力学分析模型,并对其进行模拟仿真,通过时域耦合动力分析方法分析碰撞过程的非线性动力学特性。结合动力学仿真的计算结果给出了一些指导性的建议,对于保证海上安全作业有重要意义。
1 海洋吊缆动力学模型
本文涉及的吊缆主要结构是海洋吊缆,其可以承受较大的拉力,抗弯能力很弱,具有较大的柔性,为准确地反映索结构的动态特性,本文采用集中质量法构建吊缆动力学模型。
1.1 数学模型的建立
为简化计算,将吊缆结构视为光滑、圆截面且无任何附连组件的可伸长缆绳。需要注意的是,因本文研究的吊缆在水面以上,由于海上吊放一般都是在风平浪静时,且本文主要研究的是碰撞对吊缆的影响,因此波浪引起的水动力载荷可忽略。考虑一微段圆截面吊缆受到的外部载荷,据此列出吊缆静力平衡和弯矩平衡关系式
(1)

(2)

Te=EAε
(3)
(4)
(5)

(6)
1.2 离散的集中质量数值解法
通过离散的集中质量法数值求解缆绳边界问题。凝集质量法的基本思路就是把缆绳分割成N段微元,并且每段微元的质量集中在一个节点上,这样就可以有N+1个节点。作用在每微段末端的张力T和剪力V就可以看作集中作用在某一个节点上,任何的外部载荷都视为集中作用在一个节点上。在连续性方程中,质量块模型通过有限差分法取代空间导数项从而求数值解。
经过必要化简,式(2)、(4)、(5)还可写为
(7)
(8)
(9)
通过式(8)、(9),可将式(7)化解为
(10)
进一步化简可得
(11)
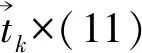
(12)

(13)
经过数值模拟分析后,易得到第k个节点运动方程表达为
MAk
(14)
其中
(15)
(16)
(17)
故运动方程式(14)里的各个外力之差可表达为
(18)
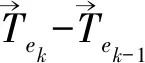
(19)
由(1)~(19),方程(14)可以用矩阵形式来表示
(20)
其中Kk表示第k分段刚度矩阵,它由以下五个子矩阵组成。
Kk=[Ak,Bk,Ck,Dk,Ek]
(21)
(22)
(23)
(24)
(25)
(26)

(27)
则可由方程(14)可知,方程(19)的外力

(28)
式(28)里的节点的速度和加速度项能够通过使用Newmark-β算法得出
(29)
(30)
故对时间步长(n)时,在惯性坐标系下的运动方程为
[K](n){R}(n)={Fe}(n)
(31)
式中:[K]是3N×3N的惯性刚度矩阵,{R}和{Fe}分别是三维节点位置矢量和外力矢量。通过数值积分对以上推导的单个节点位置矢量和速度矢量求解,能得到节点位移、速度矢量和吊缆外力随时间响应图。
1.3 吊缆碰撞力的计算

图1 缆-缆接触关系示意图Fig.1 Schematic diagram of contact relationship for cable-cable
将吊缆等效为圆形截面的柔性体模型,当两圆柱面相互接触时,采用基于罚函数的模型计算法向接触力,该模型将实际中物体的碰撞过程等效为基于穿透深度的非线性弹簧阻尼模型,这也是大多数常用的碰撞模型。且在此碰撞模型中,碰撞力最直接的体现为法向接触力,为简化计算过程,主要考虑法向接触力的影响,切向接触力暂不考虑。设两个缆的半径分别为r1、r2,当两根缆中轴线之间的距离δ
OrcaFlex中吊缆之间的碰撞力Fc可表示为
Fc=k[δ-(r1+r2)]+Fd
(32)
式中:δ为两根缆中轴线之间的距离,Fd为结构阻尼力,k为与吊缆接触刚度有关的系数,其表达式为

(33)
k1、k2分别为两根吊缆的接触系数,单位为kN/m。
结构阻尼力的表达式为
Fd=cv
(34)
式中:c为结构阻尼系数,v为两缆法向碰撞时的相对速度,且当相对速度小于零时此时说明两根缆之间正在远离因此没有阻尼力的作用,当相对速度大于零时此时说明两根缆之间正在靠近,有阻尼力的作用。
2 OrcaFlex中动态仿真模型的建立
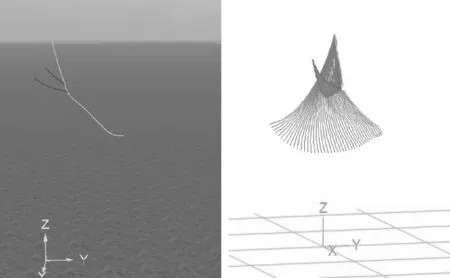
图2 吊缆碰撞模型示意图Fig.2 Schematic model of the collision for suspended cables
为简化建模过程,将吊缆一根建为横缆,一根建为竖缆,以提高碰撞发生的可能性。横缆两端从始至终全都铰接,其两端点的坐标分别为端点1(x1=-33.2 m,y1=0 m,z1=153.5 m),端点2(x2=49.2 m,y2=0 m,z2=153.5 m)。竖缆上端始终铰接于海平面以上180 m(具体坐标为x=9.8 m,y=8.7 m,z=180 m)处,下端在建模静平衡阶段铰接于海平面以上130.7 m(具体坐标为x=7.4m,y=-64.3 m,z=130.7 m)处,静平衡结束后竖缆下端解除约束,由于初始状态竖缆两端并不在一条垂线上,竖缆将绕上端点开始转动,并最终与横缆发生碰撞。两根缆的材质相同,长度均为100 m,外径均为0.35 m,线密度均为0.12 t/m,泊松比均为0.5,轴向刚度EA均为6 000 kN,弯曲刚度50 kN·m2,扭转刚度为0,法向接触系数为5 000 kN/m。为保证碰撞时节点与节点间能有效接触,两根吊缆均分为50段,单个分段长度为2 m。仿真时间为15 s。模型建成后如图2所示。
3 计算结果
经仿真发现,竖缆的第26个节点将会与横栏的第27个节点发生碰撞。
3.1 吊缆碰撞力动力学分析结果

图4 吊缆张力历时曲线Fig.4 Tension of cables versus time
观察碰撞力计算结果图3(图中左侧曲线为竖缆碰撞力时域曲线,右侧曲线为横缆碰撞力时域曲线,用了曲线加不同图标的绘图形式,即图3中左右侧的曲线均为一条,不存在不同含义的曲线重叠的情况)发现,对于竖缆而言,其发生的较明显的碰撞主要是与横缆的两次短时间的碰撞(5 s和11 s),即在竖缆第一次与横缆碰撞后两根吊缆迅速弹开,然后再次发生碰撞;除了这两次较为明显的碰撞外,竖缆的碰撞力基本维持在0 kN,这说明在整个过程中竖缆自身不同部位之间没有发生明显的碰撞。而对于横缆,计算结果表明,除了与竖缆发生碰撞外,横缆自身的不同部分之间也会发生碰撞,即随着竖缆对横缆的急剧碰撞会改变横缆的空间形态,造成与横缆27节点附近相邻的节点之间会发生轻微幅度地相互碰撞,对比横缆与竖缆的碰撞力时域图像不难发现这一点。同时,观察发现,吊缆在第一次相互碰撞时,竖缆受到的碰撞力(80 kN)要远远小于横缆受到的碰撞力(300 kN),这说明横缆受到的冲击远远大于竖缆,造成这种现象的原因为:相对于竖缆,横缆两端都被铰接,而竖缆下端自由无约束,碰撞发生后所产生的冲击随着竖缆自由端的摆动被及时释放,而横缆由于两端被铰接,无法及时释放碰撞所产生的冲击故而横缆第一次受到的碰撞力要比竖缆大,同时也正是因为其两端被铰接,使得横缆自身各部分之间更容易发生碰撞。
3.2 吊缆张力及弯曲动力学分析结果
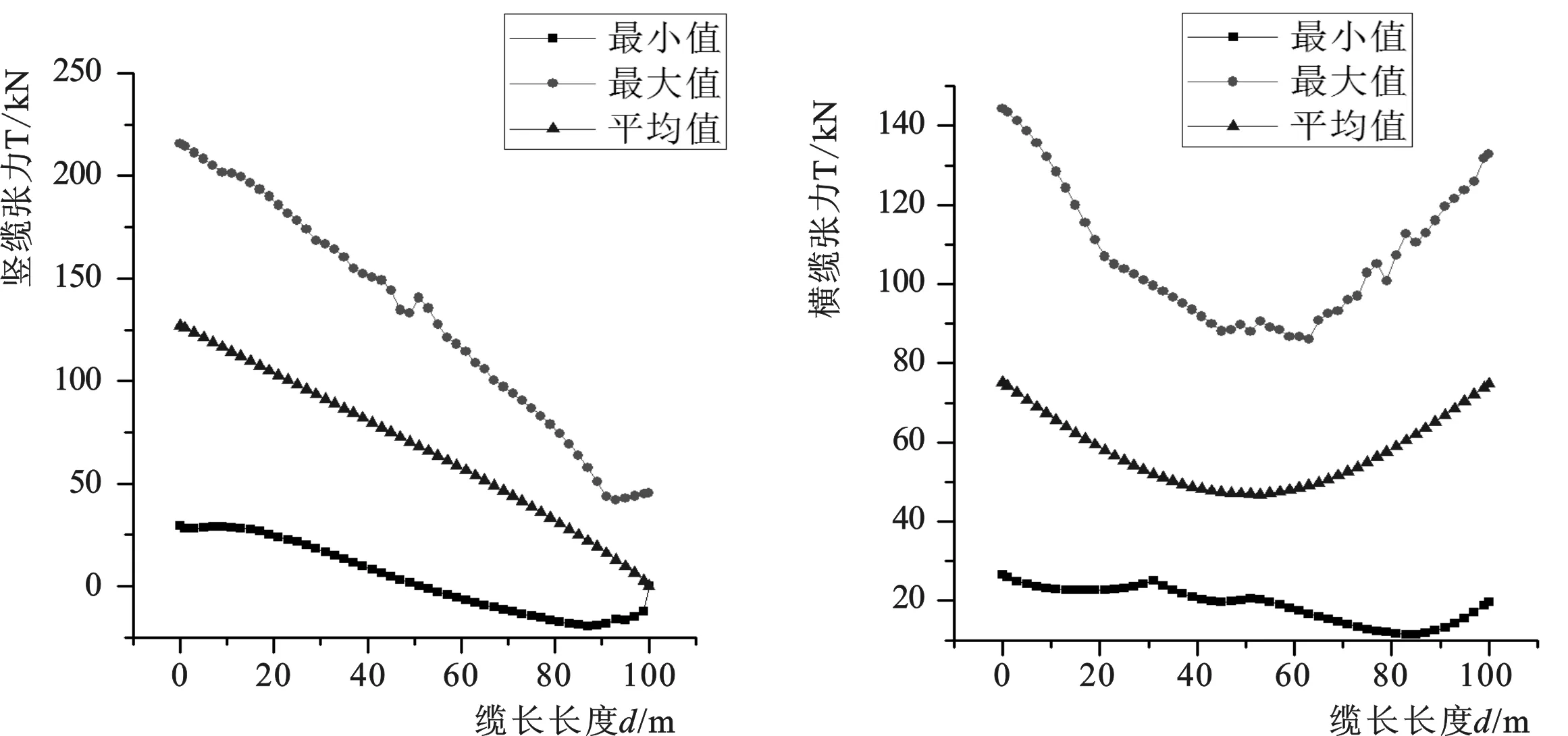
图5 吊缆张力沿缆长方向分布Fig.5 Tension of cables along the length
观察吊缆张力时域图4发现:对于竖缆,在下端解除约束后,下端不再承受牵拉的作用,因而张力图像在结束平衡阶段进入动态仿真阶段后竖缆下端始终保持在0 kN;竖缆上端的张力和26节点处的张力值随着时间的推移不断波动变化,且竖缆上端的张力始终大于碰撞点26节点处的张力,但26节点处的张力大于竖缆下端的张力,这是由于碰撞造成的剧烈抖动使得碰撞点以下对26节点造成较大牵拉引起的;而对于横缆而言,碰撞点27节点并不是在碰撞过程中张力值的最大点,反而是水平铰接端点1、2的张力值比较大,这同样是由于两端铰接使得碰撞产生的冲击得不到及时释放而造成的。同时,竖缆的张力最大值(225 kN)要大于横缆受到的张力最大值(150 kN)。也就是说,对于竖缆,张力最大值发生在上端位置,碰撞点处张力也较大,自由端为0;对与横缆来说,碰撞发生位置的张力是最小的,两端张力值基本相同。图5的张力沿缆长方向的分布情况证明了这一点。观察图5发现,沿缆长方向竖缆张力依次递减,横缆张力以碰撞点为界大体呈对称分布。
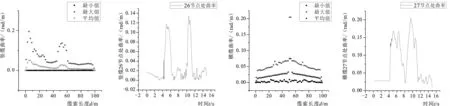
图6 吊缆曲率分布Fig.6 Distribution curvature of cables
观察吊缆曲率沿缆长方向的分布图6发现,不论是横缆还是竖缆,在碰撞处都会发生曲率沿缆长方向的突变,使得曲率沿缆长方向的分布在碰撞部位变得不光顺;同时发现,对于竖缆而言,碰撞会使上端0~10 m区域和26节点前后10 m的区域(40~60 m)发生比较明显的弯曲情况,而其余部位弯曲情况并不十分明显;对于横缆而言,由碰撞部位27节点处至两端吊缆弯曲程度依次降低。观察吊缆碰撞处曲率变化情况发现,碰撞使两根缆接触部位产生了反复的弯曲变化,且横缆在碰撞部位的弯曲变化程度要大于竖缆在碰撞部位的弯曲变化程度。对比观察图6和图7发现,沿缆长方向的曲率与弯矩图像形态呈现一定程度的相似性,这一定程度上验证了曲率与弯矩的对应关系。
3.3 吊缆运动分析
观察图8发现,在竖缆由静止到碰撞发生前这一段时间内竖缆始终处于速度不断增大而加速度不断减小的过程中,但横缆基本处于静止状态;当两根缆发生碰撞后,竖缆26节点瞬间速度变为0,然后开始发生碰撞,产生的碰撞力开始对竖缆的26节点反向加速,当速度达到最大后两根缆脱离接触,竖缆26节点在达到最大速度后再次开始减速;而横缆在碰撞发生前处于静止状态,在碰撞瞬间其速度加速到极大值,而后开始减速,速度减速到0后反向加速,加速到一最大值后再次减速。值得一提的是,在整个过程中,在碰撞的瞬间横缆27节点、竖缆26节点加速度达到最大,且横缆的最大加速度要大于竖缆的最大加速度。
观察图9沿缆长方向速度及加速度曲线发现,横缆速度的最大值出现在两缆碰撞部位,而竖缆速度最大值却出现在下端,而两缆加速度最大的区域均位于发生相互碰撞的部位:竖缆沿缆长方向速度逐渐递增,而横缆沿缆长方向,速度自碰撞点到两端依次降低,其分布形态近似呈倒抛物线形态。

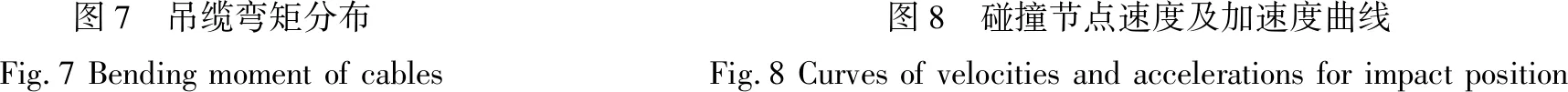
图7 吊缆弯矩分布Fig.7 Bending moment of cables图8 碰撞节点速度及加速度曲线Fig.8 Curves of velocities and accelerations for impact position
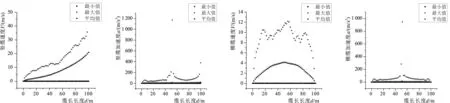
图9 沿缆长方向速度及加速度曲线Fig.9 Curves of velocities and accelerations along the length direction
4 结论
竖缆本身不同部位之间发生碰撞的可能性不大,横缆本身不同部位之间、横缆与竖缆之间都会发生碰撞。
横缆与竖缆由于约束形式的不同,导致碰撞冲击的释放有所不同,由此可见,吊缆两端的约束形式会对碰撞冲击的剧烈程度造成影响。
碰撞处会发生曲率沿缆长方向的突变,碰撞会使两根缆接触部位产生反复的弯曲变化。
约束形式的不同导致横缆与竖缆的最大速度出现部位不同,横缆速度的最大值出现在两缆碰撞部位,而竖缆速度最大值却出现在下端,两缆加速度最大值均出现在相互碰撞的部位。
