共轴旋翼无人飞行器姿态控制
2019-05-23王长龙李永科
王长龙, 武 斌, 李永科, 杨 森
(陆军工程大学石家庄校区无人机工程系, 河北 石家庄 050003)
无人旋翼飞行器能够实现垂直起降、悬停等独特的飞行功能,广泛应用于侦察、救援、航拍等领域[1]。共轴旋翼飞行器,又称为共轴直升机,相比于传统单旋翼直升机,由于取消了尾桨结构,因此具有结构紧凑、飞行效率高等优点[2-4]。然而,共轴旋翼飞行器本质上是多变量、强耦合的高阶非线性系统,而且,机动飞行时具有非定常气动特性,同时受到外部扰动的影响。因此,共轴旋翼飞行器的控制器设计成为研究的热点和难点问题。
李宏伟等[5]研究了共轴旋翼飞行器航线飞行中的航向控制问题;柯吉等[6]针对微型共轴旋翼飞行器的自主控制,提出一种包含非线性模型预测控制与线性反馈控制器的控制策略,但该方法要求飞行器模型具有较高的精度;袁夏明等[7]针对共轴旋翼飞行器非线性、强耦合的动力学特性,提出一种基于动态反馈线性化方法的鲁棒跟踪控制策略,但该方法需要完成复杂的解耦过程才能得到周期变距输入。
近年来,非线性控制理论的发展为共轴旋翼飞行器控制器的设计提供了有效的解决方法,其中反步(Backstepping)方法[8]在控制器设计中利用系统固有的非线性特性,能够有效处理非线性问题,但该方法在共轴旋翼飞行器控制器设计方面的应用鲜有报道。RAPTIS等[9]忽略了挥舞角的动态变化,设计了离散Backstepping直升机控制器;魏青铜等[10]采用反步控制设计了四旋翼无人机姿态控制器,但角速率模型未考虑通道间的耦合;JIA等[11]在考虑外部干扰的情况下设计了积分反步滑模控制器,但该方法要求外界干扰的界限已知;文献[10-11]作者采用力矩作为控制模型的输入量,然而共轴旋翼飞行器的实际输入量为旋翼变距角,由于旋翼存在不可测的挥舞角,因此无法由控制力矩得到精确的变距角;陈南宇等[12]未区分模型不确定性和外界干扰,针对系统总的不确定性设计了扩张状态观测器(Extended State Observer,ESO),利用反步控制实现了直升机轨迹的鲁棒跟踪控制。
基于以上分析,笔者将Backstepping方法用于共轴旋翼飞行器的姿态控制问题。首先,考虑旋翼挥舞、气动干扰、通道耦合和外部干扰等因素,建立了含有模型不确定性和有界扰动的非线性姿态模型;其次,采用径向基函数神经网络对模型不确定部分进行估计,采用干扰观测器对有界扰动进行估计;再次,设计了姿态Backstepping控制器;最后,通过对参考姿态信号的跟踪仿真验证了所设计控制器的有效性。
1 系统建模
1.1 机体动力学模型
设计姿态控制器对滚转角和俯仰角实施跟踪控制。将共轴旋翼无人飞行器视为刚体,考虑到研究对象的对称性,建立如下滚转和俯仰运动动力学模型:

(1)
(2)
式中:φ为滚转角;θ为俯仰角;p、q、r分别为滚转、俯仰和偏航角速率;τφ、τθ分别为滚转和俯仰力矩;Jx、Jy、Jz分别为飞行器转动惯量,J=diag(Jx,Jy)。
1.2 力矩模型
共轴旋翼飞行器机动飞行所需力和力矩主要由上、下2副共轴旋翼产生,利用下式计算:
(3)
式中:i=1,2,分别表示上旋翼和下旋翼;fix、fiy分别为上旋翼和下旋翼提供的前向力和右向力;hi为旋翼中心距离机体重心的高度;Qi为旋翼反扭矩;βic、βis分别为旋翼的纵向和横向挥舞角。相关参数表达如下:
(4)
(5)
Ti=CTi·ρair(ΩiRi)2Si/2,i=1,2;
(6)
Qi=CQi·ρair(ΩiRi)2RiSi/2,i=1,2。
(7)
式中:Ti为旋翼拉力;CTi和CQi分别为升力系数和反扭矩系数;ρair为空气密度;Ωi为旋翼转速;Ri为旋翼半径;Si为桨盘面积;τi为旋翼挥舞时间常数;Ai、Bi分别为纵向和横向操纵输入比例系数;δic、δis分别为旋翼纵向和横向周期变距角。
1.3 姿态控制模型
由于直升机旋翼挥舞及气动干扰等因素,根据控制力矩很难得到精确的周期变距角。因此,本文直接采用周期变距角作为姿态控制模型的输入,将力矩与周期变距转换过程中的不确定部分作为系统总的不确定性的一部分,在控制器设计过程中对其加以补偿,试图得到更加精确的实际输入量。
在控制器设计时,将偏航角速率作为外部扰动,将上、下旋翼的周期变距设为相同大小,即
(8)
(9)
式中:
Δf(x,u)为系统未建模动态;d1为等效扰动量;d2为外部扰动量。

2 控制器设计
令系统输出为y=x1,本文的控制目标为设计适当的控制律,使得实际输出能够有效跟踪给定的期望姿态yr。控制器设计过程如下:
1) 定义误差变量
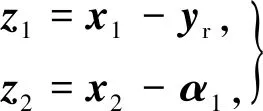
(10)
式中:α1为虚拟控制量。
对误差z1求导可得
(11)
对误差d1设计如下干扰观测器:
(12)

选取如下Lyapunov函数
(13)

对V1求导可得
(14)
设计虚拟控制量α1为如下形式:
(15)
式中:c1>0,为待设计参数。
将式(15)代入式(14),可得
(16)
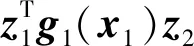
2) 考虑如下Lyapunov函数
(17)
对V2求导可得
(18)
由于Δf(x,u)和d2未知,需要对其进行估计。本文采用径向基神经网络(Radial Basis Function Neural Network,RBFNN)对未知的系统未建模动态Δf(x,u)进行逼近[13]。
令
LΔf(x,u)=WTφ(X)+ε,
(19)

υi、σi分别为径向基函数的中心和半径。
由式(9)、(19)可得
(20)
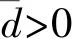
对D设计如下干扰观测器:
(21)
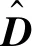
设计控制律u为如下形式:
(22)
式中:c2>0,为待设计参数。
对z2求导,由式(20)、(22)可得
(23)

将式(16)、(23)代入式(18)可得
(24)
考虑系统所有信号的收敛性,选择如下Lyapunov函数:
(25)
式中:Λ=ΛT>0,为待设计参数。
对V求导可得
(26)
由式(20)、(21)可得
(27)
式中:ζ2>0,为适当的常数。
设计神经网络权值自适应律为如下形式:
(28)
式中:σ0>0,为设计参数。
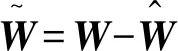
(29)
考虑如下事实:
(30)
将式(27)、(29)、(30)代入式(26)可得
(31)
式中:ζ3>0,为适当的常数。
为了保证系统的稳定性,选择控制器设计参数满足以下条件:
(32)
考虑如下事实:
(33)
式中:λmax(·)为矩阵的最大特征值。故有
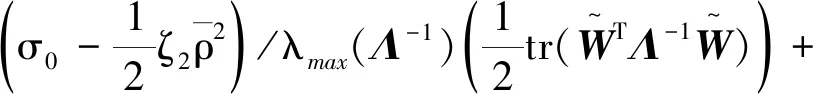
-κV+C0,
(34)
式中:
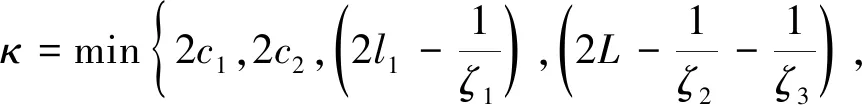
由式(34)可得
0≤V≤C0/κ+(V(0)-C0/κ)e-κt。
(35)
因此,闭环系统信号一致最终有界,通过选择合适的控制器和干扰观测器参数可以保证系统状态量收敛到原点附近较小的邻域内。
3 仿真验证
本节通过仿真验证所设计控制器的可行性。共轴旋翼飞行器的姿态模型主要参数如表1所示。由于设计的是姿态控制器,未涉及到旋翼总距,因此假设上、下旋翼拉力和反扭矩为常数。

表1 共轴旋翼飞行器姿态模型主要参数
控制器和观测器参数设置如表2所示,RBFNN参数设置为:σi=1,υi=(-0.03,-0.02,-0.01,0.01,0.02,0.03)T。

表2 控制器设计参数
选取期望姿态角(单位:(°)),外部干扰和模型不确定性如下:

系统初始状态设置为
x1=(1.635,4.874)T(°),
x2=(0.01,0.02)T(rad/s)。
为了验证所设计控制器的性能,在不考虑模型不确定性的条件下,设计了H∞状态反馈控制器,将两者的控制结果做对比。仿真结果如图1-6所示。其中:图1、2为滚转角输出量及其跟踪误差曲线;图3、4为俯仰角输出量及其跟踪误差曲线;图5、6分别为横向和纵向周期变距输入量。由图1-4可知:设计的控制器能够有效跟踪参考姿态信号,跟踪误差收敛,相比于H∞控制器,姿态跟踪误差较小。由图5、6可知:控制输入有界且快速收敛到0附近很小的邻域内,与H∞控制器相比,输入量更小,因此能量消耗较少。通过以上分析可知:设计的姿态控制器能够有效抑制外界扰动和模型不确定性,具有良好的姿态跟踪性能和较强的鲁棒性。

图1 滚转角输出量

图2 滚转角跟踪误差

图3 俯仰角输出量

图4 俯仰角跟踪误差

图5 横向周期变距输入量
4 结论
笔者基于反步法设计了共轴旋翼无人飞行器鲁棒姿态控制器。采用旋翼的周期变距角作为输入,建立了包含模型未知动态和外部扰动的非线性模型。采用RBFNN和干扰观测器分别对未建模动态和外部扰动进行估计,结合干扰估计模型设计了反步控制器,基于Lyapunov函数分析了闭环系统的稳定性。通过与H∞状态反馈控制器的对比仿真,验证了设计的控制器具有良好的姿态跟踪性能和鲁棒性。下一步,要将设计的控制器应用于实际的共轴旋翼无人飞行器中,完成实际飞行。
