基于修正Shapley值法的装备基地级维修服务PPP采购经济效益分配

冯海斌， 郑绍钰， 史 童， 陈亚旭

(1. 国防大学联合勤务学院研究生管理大队， 北京 100036； 2. 陆军装备部装备项目管理中心， 北京 100072；3. 国防大学联合勤务学院联合勤务管理系， 北京 100036； 4. 西安理工大学经济与管理学院， 陕西 西安 710054)

装备基地级维修服务PPP(Public-Private Partnerships)采购[1]合作效益是一种集多种效益于一体的帕累托最优的综合效益，主要包括军事效益、经济效益和社会效益。其中，经济效益是指在装备基地级维修服务PPP采购中，军队装备部门与社会资本通过合作完成项目得到的净经济收益与各自独立完成项目得到的净经济收益之间的差额。经济效益分配作为军队装备部门与社会资本利益关切的交汇点和分割点，直接影响双方合作关系的形成与发展[2]。根据共生理论[3]，在装备基地级维修服务PPP采购中，军队装备部门与社会资本投入与产出的分配对二者合作关系的稳定与发展具有决定性作用。装备基地级维修服务PPP采购涉及军队装备部门、社会资本和作为采购介体的第三方中介服务机构等利益相关方，各利益相关方在PPP采购交易活动中都追求更高的产出投入比，以谋求自身经济利益最大化。因此，迫切需要研究提出科学规范的装备基地级维修服务PPP采购经济效益分配方法。当前，比较普遍的PPP项目利益分配方法有Nash谈判模型、核心法、简化MCRS(Minimum Costs-Remaining Savings)方法和Shapley值法[4-7]。其中：Nash谈判模型、核心法不能保证得出唯一最优解值，存在无法得到经济效益分配方案的可能；简化MCRS方法对于装备基地级维修服务PPP采购经济效益分配问题来说，可操作性并不强;而Shapley 值法不仅能够得到唯一最优解，且建模、求解过程较为简便，虽然其存在平均分配边际贡献的局限性，但可根据装备基地级维修服务PPP采购经济效益分配的特点，对其进行修正，从而得到更加贴近实际的经济效益分配模型。因此，笔者采用修正Shapley值法分配装备基地级维修服务PPP采购经济效益。

1 分配原则

装备基地级维修服务PPP采购经济效益分配应遵循如下3项原则。

1.1 互惠互利原则

在装备基地级维修服务PPP采购中，军队装备部门和社会资本基于装备维修资源禀赋耦合，通过采购介体成立实体项目公司(Special Purpose Vehicle，SPV)或建立虚体合作伙伴关系(虚拟企业)，合作生产、提供装备基地级维修服务并共同分享经济效益[2]。因此，装备基地级维修服务PPP采购的合作模式为典型的互惠共生模式：在经济效益-维修效益分配上，按照互惠互利的原则，兼顾各利益相关方的应得利益，合理分配经济效益，确保双方在项目中皆“有利可图”，从而在军队装备部门与社会资本之间形成一种稳定发展的合作关系。

1.2 分配对称原则

与传统装备采购相比，装备基地级维修服务PPP采购是军队装备部门与社会资本基于装备维修资源禀赋耦合，共用资源合作生产、提供装备基地级维修服务。在市场经济条件下，军队装备部门与社会资本具备的资源禀赋往往不同，二者投入装备基地级维修服务PPP采购项目的优势资源也不相同。因此，在经济效益-维修效益的分配上，要按照分配对称的原则，考量各利益相关方的资源投入和风险分担，在军队装备部门与社会资本之间尽量对称分配经济效益，确保双方投入与产出成正比，从而在军队装备部门与社会资本之间形成一种正向的合作激励。

1.3 结构最优原则

在装备基地级维修服务PPP采购中，除了军队装备部门、社会资本2个确定型利益相关方，作为采购介体的第三方中介服务机构等预期型利益相关方外，还涉及行政部门等潜在型利益相关方，由于各利益相关方的价值取向各不相同[8]，其利益诉求也不相同。因此，在经济效益-维修效益的分配上，要按照结构最优原则，找到各利益相关方的最佳利益均衡点，在军队装备部门与社会资本之间以最优比例结构分配经济效益，确保双方经济收益均能达到帕累托最优，从而在军队装备部门与社会资本之间形成一种最优的合作结构。

2 Shapley值法原理与适用性

2.1 Shapley值法原理

Shapley值法是一种解决n人合作博弈的方法[9]，其按照贡献与收益对等的分配原则，根据各理性参与者的边际贡献大小来分配合作联盟的收益，即联盟中第i个参与者获得的收益分配值为参与者i对所有含i的合作联盟所做边际贡献的平均值。其数学定义如下：

设I={1,2,…,n}为合作联盟中n个参与者的集合，若对于集合I的任一子集s均对应一个实值函数v(s)，且满足如下条件：

v(∅)=0；

(1)

v(s1∪s2)≥v(s1)+v(s2),s1∩s2=∅。

(2)

则称[I,v]为n人合作博弈，其中，v为合作联盟s的收益，是定义在I上的特征函数。

设φi(v)为集合I中第i个参与者所得的收益，v(I)为合作联盟的最大收益，则合作博弈[I,v]中各参与者所得收益分配的Shapley值为

Φ(v)=(φ1(v),φ2(v),…,φn(v)),
i=1，2，…，n。

(3)

且φi(v)具有如下2个特性：

1) 整体理性，即

(4)

2) 个体理性，即

φi(v)≥v(i),i=1,2,…,n。

(5)

式中：

(6)

(7)

其中，Si为集合I中包含第i个参与者的所有子集；|s|为子集s中参与者的数量；s{i}为s中不含第i个参与者的集合；w(|s|)为加权因子；v(s)为子集s得到的收益；v(s{i})为s中不包含第i个参与者的集合所得的收益。

Shapley值法是研究动态合作联盟中各参与者收益分配最常用的建模方法之一，其假设联盟参与者均为理性人，按照贡献与收益对等的分配原则，根据各参与者为动态联盟产生的边际贡献，确定利益相关方的收益分配比例，从而达到合作联盟整体理性与各参与者个体理性双重满意的效果。该方法的局限性是假设动态合作联盟的参与者都是平等的，即Shapley值权重系数相等，合作联盟中对参与者i的收益分配值为参与者i对所有包含它的合作联盟所做边际贡献的平均值1/n。但在实践中，对于包含参与者i的不同合作联盟，参与者i的贡献度是各不相同的。因此，在实践运用中常需要结合实际对Shapley值进行修正。

2.2 Shapley值法的适用性

作为一种典型的军事经济复合共生系统，装备基地级维修服务PPP采购项目的参与者都是理性人，当没有利益相关方参与时，PPP采购项目收益自然为0，且只有当PPP采购项目为利益相关方带来的收益>其单独完成该项目获得的收益时PPP采购项目才可能运营下去，所以，装备基地级维修服务PPP采购满足式(1)、(2)的条件。同时，只有产生新增的净经济收益，即PPP采购项目产生的总经济收益>各利益相关方单独完成该项目获得的经济收益与交易成本之和，且PPP采购项目为各利益相关方带来的经济收益均比其独立完成该项目所获经济收益更大时，装备基地级维修服务PPP采购中军队装备部门与社会资本间的合作关系才能保持稳定并健康发展。所以，装备基地级维修服务PPP采购具备式(4)、(5)的特性。因此，装备基地级维修服务PPP采购是一种典型的n人合作博弈，运用修正Shapley值法分配装备基地级维修服务PPP采购项目经济效益是切实可行的。

3 分配思路与步骤

3.1 分配思路

根据Shapley值法基本原理，装备基地级维修服务PPP采购经济效益分配的基本思路如图1所示。首先，对装备基地级维修服务PPP采购项目总收益进行事前估算或者事后核算，确保该PPP采购项目满足Shapley值法的适用条件；其次，通过事前估算或者事后核算总收益来评估装备基地级维修服务PPP采购项目利益相关方的边际贡献；再次，采用Shapley值法初始分配装备基地级维修服务PPP采购项目的经济效益，得到初始分配方案；最后，根据各利益相关方投入的维修资源占装备基地级维修服务PPP采购项目总资源的比例，调整初始分配方案并形成装备基地级维修服务PPP采购项目经济效益分配方案。

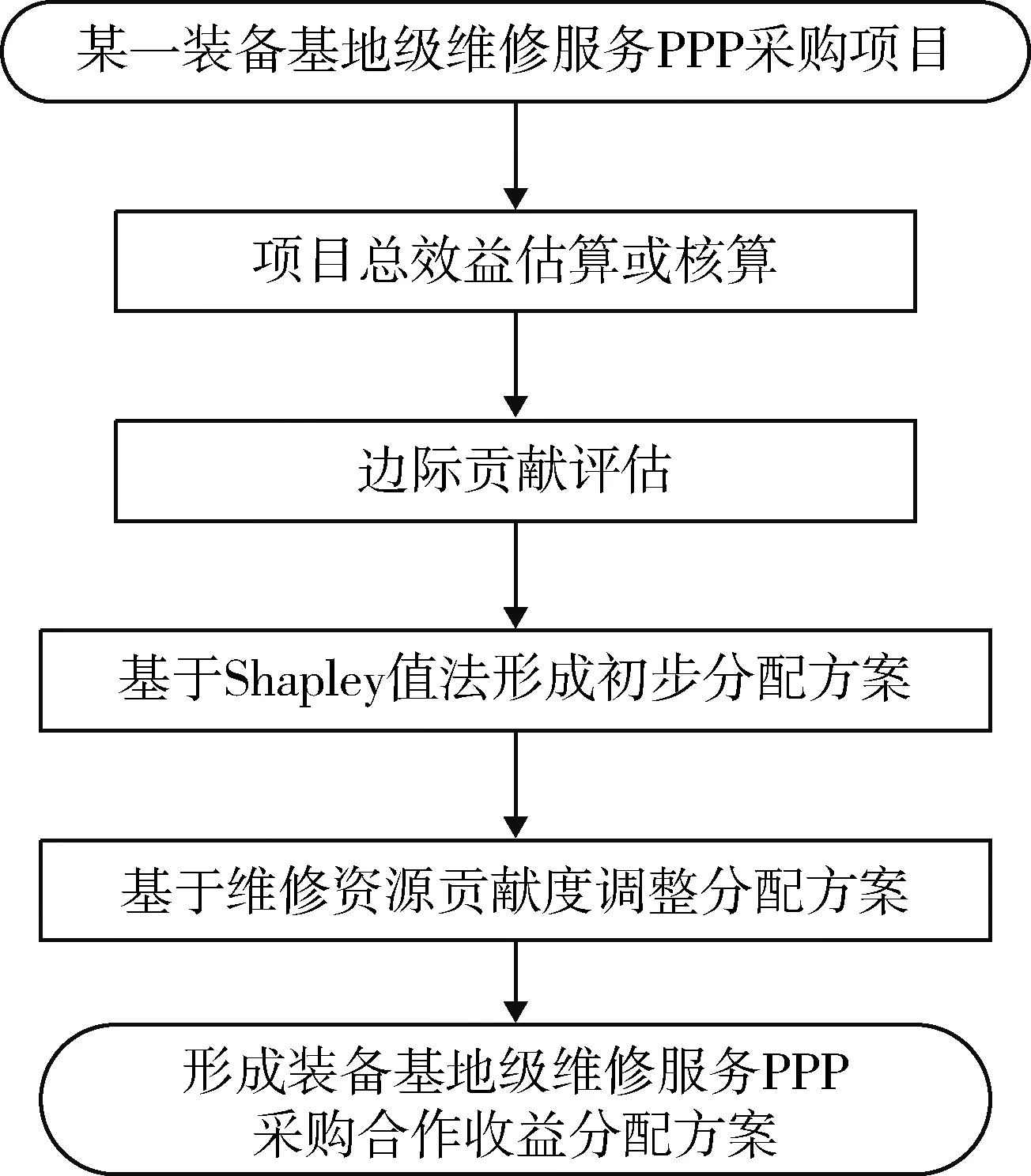
图1 装备基地级维修服务PPP采购经济效益分配基本思路

3.2 分配步骤

为便于讨论，假设装备基地级维修服务PPP采购中只有1个军队装备部门x与1家社会资本y合作，即装备基地级维修服务PPP采购是一个2人合作博弈,其经济效益分配步骤如下。

3.2.1 合作博弈特征函数确定

针对军队装备部门x与社会资本y采取的不同策略，形成不同的非空集合，其对应的特征函数分别为：

1)当军队装备部门x独自完成装备基地级维修项目，即s={x}时，其获得的收益——特征函数为v(x)；

2)当社会资本y独自完成装备基地级维修项目，即s={y}时，其获得的收益——特征函数为v(y)；

3)当军队装备部门x与社会资本y通过PPP模式组成合作联盟共同生产并提供装备基地级维修服务，即s={x,y}=I时，其获得的总收益——特征函数则为v(x∪y)。

3.2.2 军队装备部门和社会资本经济效益分配的Shapley值计算

根据式(6)、(7)分别计算军队装备部门和社会资本经济效益分配的Shapley值φx(v)和φy(v)，具体计算过程如表1、2所示。

表1 军队装备部门经济效益分配Shapley值的计算

表2 社会资本经济效益分配Shapley值的计算

军队装备部门经济效益分配的Shapley值为

φx(v)=v(x)/2+(v(x∪y)-v(y))/2。

(8)

社会资本经济效益分配的Shapley值为

φy(v)=v(y)/2+(v(x∪y)-v(x))/2。

(9)

3.2.3 经济效益初步分配方案及其分析

根据军队装备部门和社会资本经济效益分配的Shapley值，可得装备基地级维修服务PPP采购经济效益分配的初步方案，即装备基地级维修服务PPP采购经济效益分配的Shapley值,其数学表达式为

Φ(v)=(φx(v),φy(v))=

(10)

根据Shapley值法原理和式(10)可知：Shapley值法假设在装备基地级维修服务PPP采购中，各利益相关方对维修资源的贡献度是相同的，均为1/2。因而，其在经济效益的分配上也是平等的，即默认的收益分配因子为1/2。但根据资源禀赋理论[10]，通常只有异质性的资源才能相互耦合，所以，在实际的装备基地级维修服务PPP采购中，军队装备部门与社会资本之间恰恰是基于维修资源禀赋的耦合才强强联手，合作生产并提供装备基地级维修服务。由此可见：军队装备部门与社会资本在装备基地级维修服务PPP采购中，各自对维修资源的实际贡献度是不同的，若按照Shapley值来分配各利益相关方的经济效益，则会出现一些利益相关方由于投入与产出不成正比，而退出或者不参与装备基地级维修服务PPP采购项目，因此需要对Shapley值法进行修正。

3.2.4 初步分配方案调整及最终分配方案形成

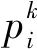
其中,i=1,2,分别为军队装备部门和社会资本；k=1,2,…,m,为装备基地级维修所需m种维修资源。

军队装备部门或社会资本在装备基地级维修服务PPP采购项目中实际的维修资源贡献度为

(11)

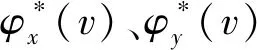
v(x∪y)，i=1,2；

(12)

v(x∪y)，i=1,2。

(13)

由式(12)、(13)可得：

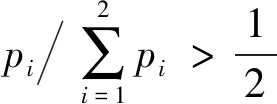
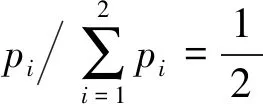
将式(8)、(9)、(11)代入式(12)、(13)可得

(14)

(15)

则装备基地级维修服务PPP采购经济效益分配的合理方案，即基于维修资源贡献度修正的装备基地级维修服务PPP采购经济效益分配的Shapley值为

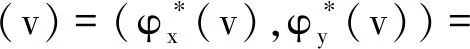
显然

v(x∪y)=φx(v)+φy(v),

这表明修正后军队装备部门与社会资本分配到的经济效益之和与修正前相等。因此，基于维修资源贡献度的修正是可行的。

4 示例分析

以某项装备基地级维修服务PPP采购项目为例，验证本文提出的装备基地级维修服务PPP采购经济效益分配方法的可行性与实用性。

设该装备基地级维修服务PPP采购项目中，由一个军队装备部门x与一家社会资本y合作，经事前估算其投入与产出情况如表3所示。

表3 某装备基地级维修服务PPP采购项目的投入与产出情况 百万元

当军队装备部门x独自完成装备基地级维修项目时，其获得的收益v(x)=2；当社会资本y独自完成装备基地级维修项目时，其获得的收益为v(y)=3；当军队装备部门x与社会资本y通过PPP模式进行合作时，其获得的总收益则为v(x∪y)=8。

根据式(6)、(7)计算军队装备部门和社会资本经济效益分配的Shapley值，计算过程分别如表4、5所示。

军队装备部门x和社会资本y的经济效益分配的Shapley值分别为

表4 军队装备部门x的经济效益分配Shapley值的计算

表5 社会资本y经济效益分配Shapley值的计算

φx(v)=v(x)/2+(v(x∪y)-

v(y))/2=1+5/2=3.5；

φy(v)=v(y)/2+(v(x∪y)-

v(x))/2=3/2+3=4.5。

该装备基地级维修服务PPP采购经济效益分配的Shapley值为

Φ(v)=(φx(v)，φy(v))=(3.5，4.5)。

军队装备部门与社会资本的维修资源贡献度分别为

基于维修资源贡献度修正的该装备基地级维修服务PPP采购项目的经济效益分配的Shapley值为

5 结论

笔者在判明装备基地级维修服务PPP采购经济效益分配是一个典型的n人合作博弈的基础上，运用Shapley值法得到军队装备部门与社会资本经济效益分配的Shapley值(即装备基地级维修服务PPP采购经济效益初步分配方案)，基于军队装备部门和社会资本在装备基地级维修服务PPP采购中实际维修资源贡献度对其经济效益分配的Shapley值进行了修正，得到军队装备部门和社会资本理应分配到的经济效益，并通过示例验证了该方法的可行性与实用性，为合理分配装备基地级维修服务PPP采购经济效益提供方法支持，对于其他类型国防服务PPP采购经济效益的分配也具有一定的参考价值。