华山地区降水特征分析与年降水量预测

屈文岗, 徐盼盼, 钱 会

(1.长安大学 环境科学与工程学院, 西安710054; 2.旱区地下水文与生态效应教育部重点实验室, 西安 710054)

华山地区的生态环境有着脆弱易破坏且难恢复的特点[1]。由于水土流失造成的山区生态环境问题具有分布广和危害高的特征，易造成土壤退化，粮食减产，严重时还可能造成河道堵塞、水库淤积等严重后果，对经济社会持续稳定的发展造成威胁[2]。研究表明，降水是水土流失的第一主导因素，其分布情况的差异性造成水土流失的规律具有多变性[3]。陕西华阴县自古以来就有“三年一小旱，十年一大旱”的规律，除此之外，受地形和气流的影响，华阴县水涝灾害也比较严重，位于华阴县内的华山自然深受其害。恶劣天气条件尤其是极端降水会对山体稳定性造成威胁，极易引发滑坡，泥石流等自然灾害。因此，研究华山地区的降水分布特性及预测未来走势对该地区水土流失防治，防灾减灾项目实施和山区资源综合开发利用具有指导性的意义。

研究降水演变规律的方法众多，如滑动平均法、有序聚类分析法、Man-Kendall非参数方法以及云模型等。滑动平均法是数据处理方法中非常重要的方法，它主要是对观测数据资料进行分段拟合，以达到减少或消除随机误差的目的[4]。孙乐强等[5]通过分析滑动平均马尔可夫模型不同步长下年降水量预测精度，得出在一定的范围内，模型的预测精度会随着步长的增加而提高，且3 a滑动平均提高预测精度效果最好。有序聚类分析法具有公式简单易懂，计算精确的优点，在突变点识别中应用广泛[6]。唐共地等[7]利用有序聚类分析法，得出潜山水文站流域1996年是输沙量系列中的突变点。Man-Kendall非参数方法是世界气象组织推荐并广泛运用的非参数检验方法[8]。徐泽华等[9]在使用Man-Kendall对降水趋势进行研究时发现，山东地区降水近30 a呈现上升趋势。云模型建立于传统模糊数学与概率统计交叉的基础之上，能实现定性与定量之间的转化[10]，其主要运用于电子软件，仿真方面[11]，在降水特征分析的领域亦有应用。徐盼盼等[12]基于云模型研究了宝鸡地区降水分布特征，发现枯水期降水量少，不均匀性低，稳定性高；丰水期分布离散且稳定性最低；全年降水量分布最离散且稳定性较小。加权马尔科夫链预测模型被广泛应用在降水量预测中，且预测精度较高[13]。钱会等[14]利用此预测模型来预测宁夏石嘴山地区年降水量，得出2009年和2010年的年降水量分别为135.11 mm和146.88 mm。吴林川等[15]运用加权马尔科夫链模型预测榆林地区年降水量范围，2014年、2015年年降水量范围分别为457.52～521.32 mm和351.19～457.52 mm。张杰等[16]运用加权马尔科夫链预测济南市2015年和2016年降水量状态为平水年，年降水量分别为691.21 mm和645.28 mm。

刘政鸿等[17]研究了陕西省1961—2010年降水量年际变化规律，发现降水量存在明显的“增多—减少—增多—减少—增多”的特征，且总体呈现减少趋势。田中伟等[18]依据1962—2011年秋季渭南市的气象数据，发现秋季渭南市降水具有纬向分布的特点。刘全玉等[19]根据华山地区400年的降水序列，结合奇异谱分析未来30 a华山地区降水变化趋势，预测在2010—2039年，华山地区降水略有增加。

本文采用华山地区1953—2013年逐日降水资料，利用Mann-Kendall 检验方法、有序聚类法、云模型等方法，深入分析华山地区降水变化的月、季节和年际变化特征，并结合滑动马尔可夫预测模型预测华山地区2014—2023年未来10 a的年降水量，其成果不仅可以增加华山地区气候、水资源保护与配置研究的内容，而且为华山地区水利设施建设、蓄洪抗旱提供依据，更重要的是为该区域水土保持方案规划，自然灾害预防与处理措施的开展，自然资源合理配置等提供指导性意见。

1 研究区概况

华山位于陕西省华阴市正南方，处于109°57′ —110°05′E,34°25′—35°00′N，属大陆季风气候，冬季寒冷干燥，夏季高温多雨，春季温暖多风，秋季温凉湿润，四季分明。年均气温13.7℃，月平均气温1月最低为-0.6℃，7月最高为23.7℃。年降水量476.8～862.2 mm，东西长约15 km，南北宽约10 km。

2 资料与方法

2.1 降水资料的收集

华山站1953—2013年的逐日降水资料，来源于中国气象科学共享服务网。经统计得出61 a月降水量、季节降水量和年降雨量数据。

2.2 分析方法

2.2.1 降水量趋势分析与突变分析 降水虽然是一种非平稳的随机现象，但其时间序列有一定的趋势性[20]。本文使用Mann-Kendall 检验法、有序聚类法对华山地区降水趋势和突变进行深入研究。其中Mann-Kendall检验法用于分析降水序列的变化趋势，其属于非参数检验方法，具有对样本要求少，抗干扰能力强，计算简便等特点[21]；有序聚类法用于分析降水序列的突变分析，其核心是离差平方和，根据离差平方和的大小找出突变点[22]。这两种方法在相关文献[21-22]有详细介绍，这里不再赘述。

2.2.2 降水量分布特征云分析 设U是一个定量论域，这个论域用精确数值表示，C是关于U的一个定性概念，对于U中任意一个元素x，都存在一个随机数μ(x)∈[0，1]，这个μ叫做x对C的隶属度，而x在C上的分布称为云，且x称为云滴[23]。云的数字特征用期望Ex、熵En和超熵He来表征[23-24]。本文采用正态云模型来分析降水量特征，其算法步骤参见相关文献[12,25]。

2.2.3 滑动平均马尔可夫模型 本文用到的滑动平均马尔可夫模型建立步骤见文献[12]。建模过程中所用到的公式(1—5)：

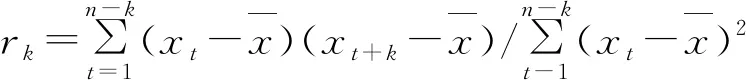
(1)

(2)

(3)

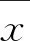
(4)

式中：Z值一般取2，表示最大概率的作用系数。

(5)

式中：i为预测状态。

3 结果与分析

3.1 降水特征分析

3.1.1 年内变化分析 图1为华山地区61 a月平均降水量柱状图，由图可知：多年月平均降水量呈单峰型，年内降水分布极度不均，主要集中在7月、8月、9月，占年均降水量的48.46%，其中以7月和8月最多，降水量为160.2 mm和126.5 mm，分别占年均降水量的20.30%，15.24%。12月最少，降水量为11.3 mm，占年均降水量的1.4%。

表1给出了华山地区季节降水量的统计信息，可知，夏季降水占全年降水的比例最大，为44.90%，秋季次之，为27.51%，春季和冬季分别为22.52%和5.07%。可见年内季节降水分布不均匀，夏秋两季降水量决定了年降水量的多寡。图2为华山地区季节降水趋势变化图，由图可知春夏秋冬四季降水量均呈下降趋势，递减率分别为-11.84 mm/10 a，-18.94 mm/10 a，-12.90 mm/10 a，-2.33 mm/10 a。其中，夏季降水量下降趋势最明显，冬季降水量下降趋势最小。经Mann-Kendall检验得到华山地区春、夏、秋、冬四季降水量的Z值分别为-4.26，-6.07，-8.34，-1.44，见表1。比较可知，四季降水量趋势检验结果与线性趋势分析结果一致。

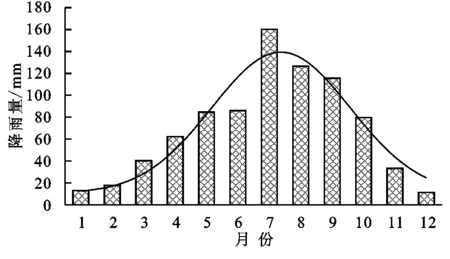
图1 华山地区1953-2013年月平均降水量柱状图

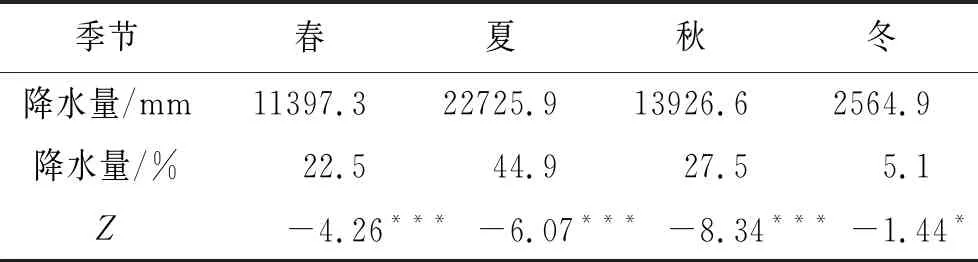
季节春夏秋冬降水量/mm11397.322725.913926.62564.9降水量/%22.544.927.55.1Z-4.26***-6.07***-8.34***-1.44*

注：不同标记表示数据通过了不同可信度的显著性检，*，**和***分别表示通过的显著性检验可信度90%，95%和99%。

3.1.2 年际变化分析 华山地区1953—2013年年均降水量为829.8 mm，降水量最大年份为1964年、1 262.3 mm，最小年份为2013年，561.9 mm。图3为华山地区年降水量变化趋势图。由图可知，年降水量一直处于波动状态，整体呈递减趋势。从局部来看，1953—1990年，华山地区年降水量以29.1 mm/10 a的速率呈明显下降趋势，而1991—2013年，年降水量以42.6 mm/10 a的速率呈明显增加趋势。61 a来，年降水量多于年均降水量的年份有32个，小于年均降水量的年份有29个。由Mann-Kendall 检验法可得，华山地区年降水量的Z值为-3.62，表示年降水量呈下降趋势，且通过了99%的显著性检验，其结果与线性趋势分析结果一致。采用有序聚类法对年降水量序列进行突变分析，结果见图3。可以看出1987 年的离差平方和最小，说明在1987 年降水量发生突变，1987年以前年降水量均值为906.7 mm，1987年后至今，年降水量均值为726.1 mm，前后相差180.6 mm，可知年降水量呈减少的势态。

3.2 云模型分析

根据逆向云发生器得到华山地区四季及全年降水量隶属云的数字特征(表2)，然后由正向云发生器绘制其隶属云图(图4)。期望Ex表示降水序列各要素的均值；熵En反映了降水序列各要素相对均值的离散度，值越大，表示分布越不均匀；超熵He表示熵的离散程度，值越小，不均匀性的稳定性越高。由表2和图4可知：春冬季降水量少，分布均匀，稳定性高，夏秋季节降水量多，分布不均匀，稳定性低。综合来看，全年降水量主要由夏秋两季贡献而来，且夏秋两季降水量的分布变化直接导致年降水量的分布不均，此现象说明夏秋两季易发生短时极端降水天气，进而造成洪涝、泥石流、山体滑坡等自然灾害，易对生命财产安全造成威胁。

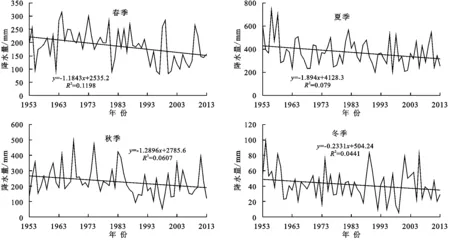
图2 华山地区季节降水趋势变化

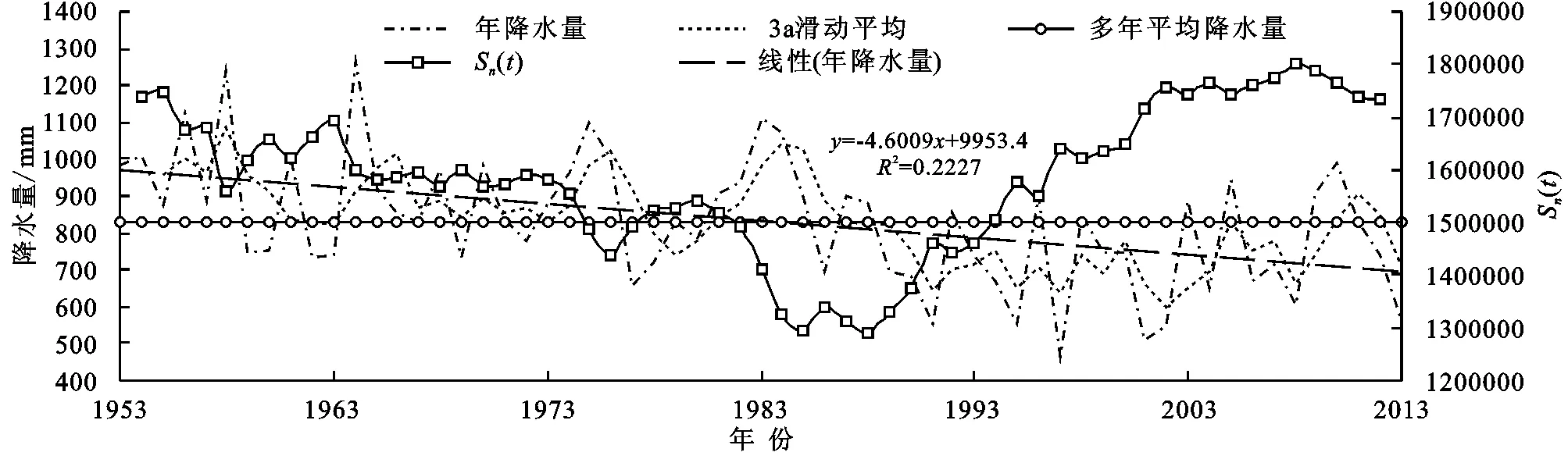
图3 华山地区1953-2013年年降水量变化趋势及突变检验

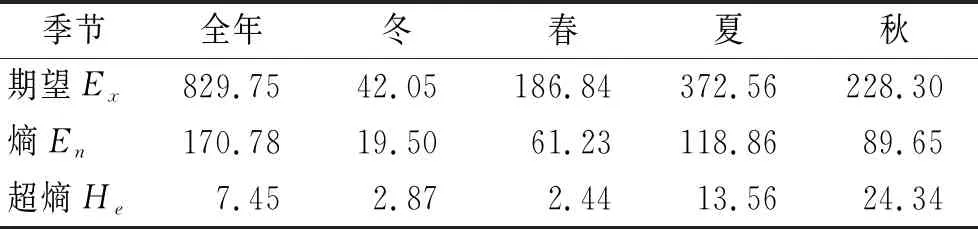
表2 华山地区四季及全年降水量隶属云数字特征

4 华山地区年降水量预测

4.1 年降水量分级标准及状态

本文年降水量分级标准见表3，1955—2013年3 a滑动平均降水系列状态见表4。经计算，华山地区3 a滑动平均年降水量序列的χ2=34.29，通过了显著水平α=0.05的χα2检验，因此滑动平均年降水量序列具有马氏性，可以使用该方法对华山地区降水量进行预测。

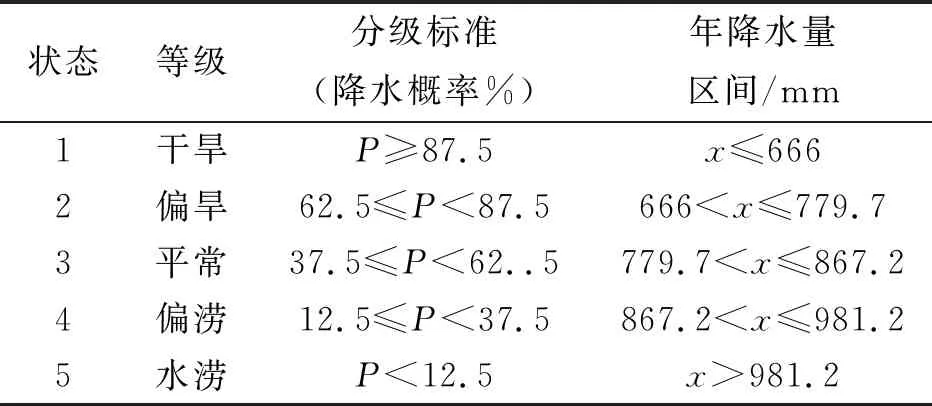
表3 1955-2013年3 a滑动平均降水量等级划分

4.2 模型的检验

分别应用1955—2011年和1955—2012年滑动平均降水量序列和其对应的概率转移矩阵对2012年和2013年的滑动平均降水量进行预测(表5，表6)。表7是华山地区2012年、2013年降水量预测结果及误差分析。可知，2012年华山地区3 a滑动平均年降水量预测状态为3，实测状态为3。根据模糊集理论，计算得2012年3 a滑动平均年降水量预测值为895.2 mm，实测值为851.7 mm，相对误差为5.1%。2013年华山地区3 a滑动平均年降水量预测状态为2，实测状态为2。计算得2013年3 a滑动降水量预测值为773.8 mm,实测值为709.2 mm，相对误差为9.1%。以上预测结果满足相对误差不超过20%的精度要求[26]，可见，滑动平均马尔可夫模型适用于华山地区降水量的预测。

4.3 降水量预测

基于滑动平均马尔可夫预测模型，对华山地区2014—2023年的降水量进行预测，预测值见表8。未来10年华山地区降水量变化趋势与近23 a(1991—2013)的年降水量变化趋势类似，均为增加趋势。此趋势符合前文描述的华山地区61 a来降水量变化特征，并且预测结果的变化趋势和刘全玉等[19]的研究结果一致。1991—2013年华山地区降水量增加幅度为42.6 mm/10 a，2014—2023年降水量增加幅度为29.3 mm/10 a。由表8可知，在10年预测期内2019年预测值最小，为634.3 mm，2023年预测值最大，为883.3 mm。

5 结 论

华山地区1953—2013年月降水分布极度不均，主要集中在7月、8月、9月，降水量分别为160.16 mm，126.49 mm和115.55 mm。夏与秋降水量约占全年的72.41%，其降水量决定了年降水量的多寡。华山地区春夏秋冬四季降水量变化均呈下降趋势，分别为-11.84 mm/10 a，-18.94 mm/10 a，-12.90 mm/10 a，-2.33 mm/10 a。经Mann-Kendall检验得到华山地区四季降水量变化趋势与线性分析一致，除冬季外均通过99%显著性检验。华山地区1953—2013年年均降水量为829.75 mm，降水量最大值为1 262.3 mm，最小值为561.9 mm。年降水量年际变化较大，整体呈递减趋势。3 a 滑动平均年降水量变化也呈减小趋势，变化幅度相对于年降水量有所减小，且通过了99%的显著性检验。1987年以前年降水量均值为906.7 mm，1987年后至今年降水量均值为726.1 mm，前后变化达180.6 mm，可知年降水量也呈明显的减少趋势，与上述研究结果一致。云模型结果表明，冬春季降水量少，分布均匀，稳定性高；夏秋季节降水量多，分布不均匀，稳定性低；夏秋两季降水量的变化直接导致年降水量的分布不均。

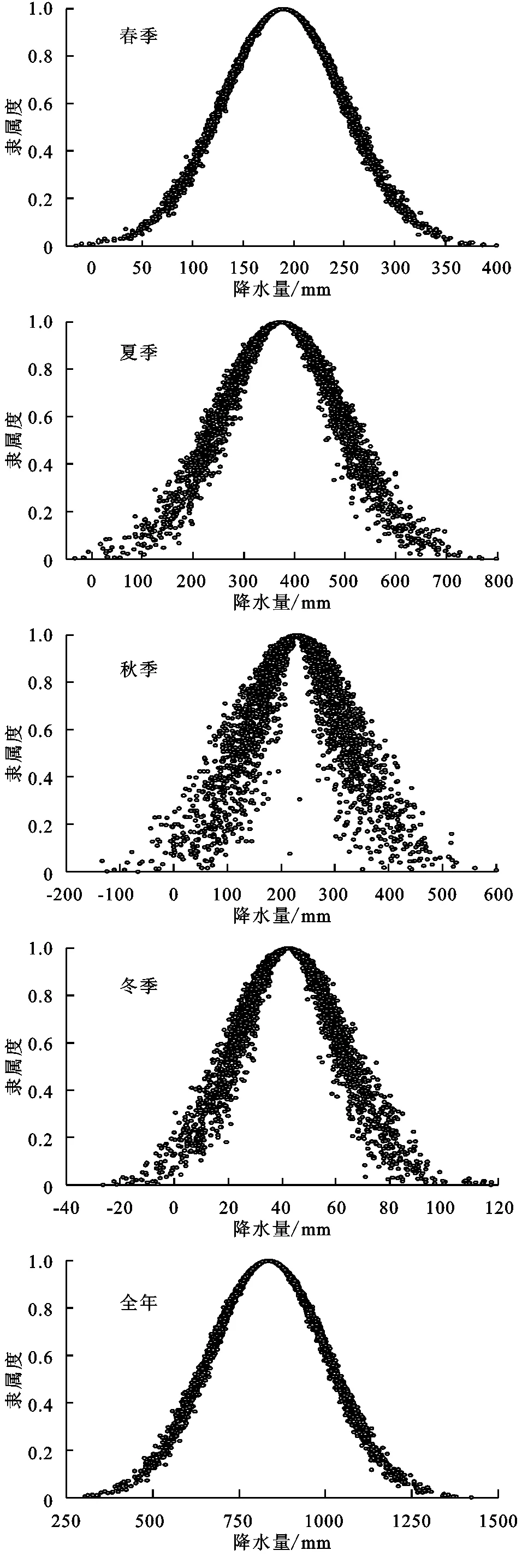
图4 华山地区降水量隶属云图

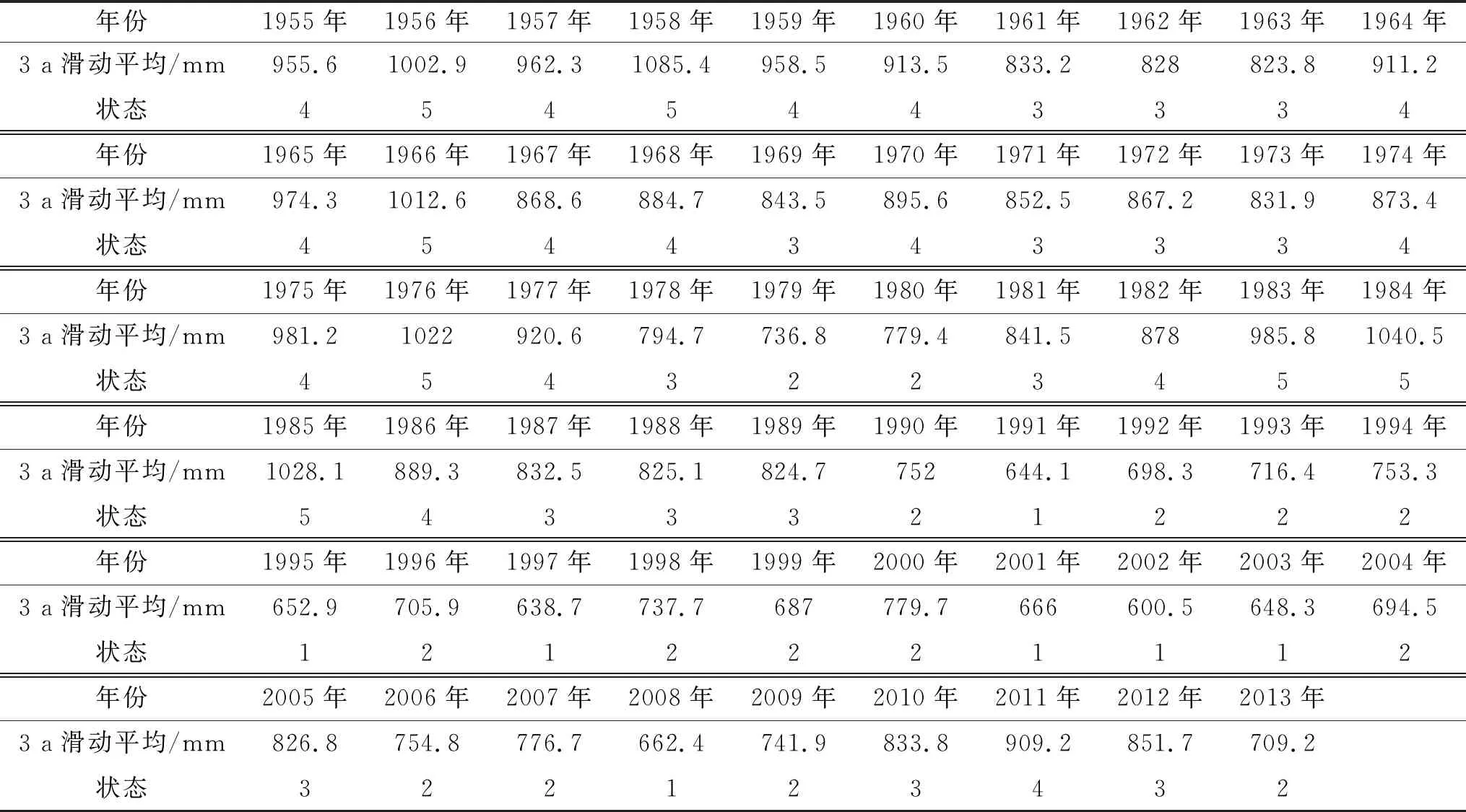
表4 1955年-2013年3 a滑动平均降水量及状态

表5 华山地区2012年3 a滑动平均年降水量预测

表6 华山地区2013年3 a滑动平均年降水量预测

表7 华山地区2012-2013年3 a滑动平均年降水量预测结果及误差

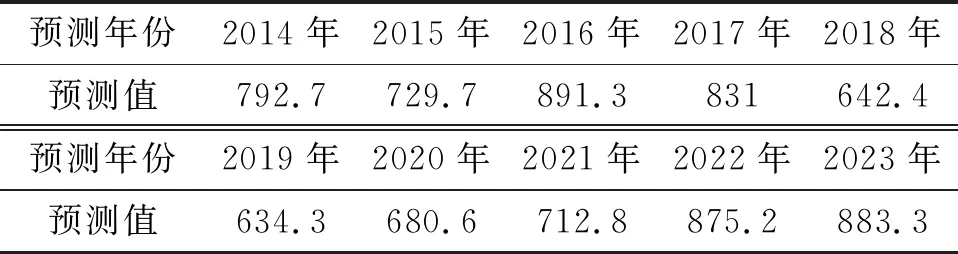
表8 华山地区2014-2023年降水量预测

应用2012年、2013年3 a滑动平均实测数据，验证了滑动平均—马尔科夫预测模型适用于华山地区。运用该模型预测华山地区未来10 a年降水量，未来10 a降水量与1991—2013年降水量均呈增加趋势。1991—2013年华山地区降水量均值为734.8 mm，增加幅度42.6 mm/10 a；2014—2023年预测降水量均值为767.3 mm，增加幅度为29.3 mm/10 a。且在预测结果中，2019年预测值最小，为634.3 mm；2023年预测值最大，为883.3 mm。

Mann-Kendall法，有序聚类分析法，云模型和滑动平均—马尔科夫模型等方法的有机结合，系统地研究了华山地区61 a来降水变化规律并预测了未来10 a降水量的变化情况。该研究结果不但丰富了华山地区气候研究的内容，而且对该地区水土保持方案规划与实施、自然灾害防治具有指导性。