海上中等强度砂岩出砂预测研究

闫新江，曹砚锋，刘书杰，邓金根，刘伟，翟晓鹏

(中海油研究总院有限责任公司，北京 100028)(中国石油大学(北京)石油工程学院，北京 102249)(长江大学石油工程学院，湖北 武汉 430100)

海上平台由于空间有限，环保要求高，如果地层产出砂进入地面生产流程，则必须将其从产出液中分离，并对分离后的砂粒进行处理[1～5]。平台生产流程在设计阶段需要考虑出砂量对处理设施的磨损，对出砂量控制要求高。因此，需要精确计算出砂时间及出砂压差，进而指导地面产出砂监测及防砂方式的选择。

中等强度砂岩岩石强度较高，弹性模量较大，较高围压下软化特征减弱。开采后期随着储层压力的衰减及产水，也存在出砂现象。目前国内外研究主要针对疏松砂岩及稠油油藏出砂冷采，主要为测井资料经验公式计算，或单纯考虑剪切破坏下的出砂预测。笔者针对中等强度砂岩特点，采用流固耦合计算方法对岩石井筒应力分布进行计算，使用有限元方法对出砂时机进行预测。

1 中等强度岩石变形本构模型

根据单轴抗压强度(UCS)，砂岩的强度等级划分为4类，见表1。未固结或弱固结砂岩储层在生产过程中总是伴随着出砂现象；高强的砂岩储层在生产过程中几乎不会出现出砂现象，增大生产压差，或随开采过程中的有效应力增加都不能够达到高强砂岩的破坏条件。而介于弱固结砂岩和高强砂岩之间的中等强度砂岩，在开采初期，在较小的生产压差和较小的有效应力条件下无出砂现象，但随着生产过程中的地层孔隙压力下降、有效应力增加或者生产压差增大，原来不出砂的地层开始出砂。

表1 岩石强度等级划分

中等强度岩石与其他固体金属材料不同的是：岩石具有孔隙空间，而且孔隙空间内饱和有地层流体。在外部地应力及开采条件下，岩石固体与孔隙流体之间会发生相互作用。砂岩在一定的应力条件下会进入塑性状态，较大的变形会引起孔隙度、渗透率的变化并影响储层流体的流动及压力分布[6～9]。

砂岩储层的变形主要为弹塑性变形，在油气开采过程中，孔隙压力的变化是缓慢的，因此岩石骨架的变形过程非常小，可认为是准静态的。对于三维问题，弹塑性体空间域内的平衡方程为：

σij+Fi=0

(1)

式中：σij为单元体应力；Fi为体积力分量；i,j为张量指标符号。

应变分量和位移分量之间的关系通过张量来描述：

(2)

式中：εij为单元体应变；ui,j和uj,j为位移分量。

砂岩的应力-应变本构方程采用弹塑性本构方程，使用增量形式表示为：

(3)

[Dep]=[De]-[Dp]

(4)

式中：De、Dp为弹性和塑性的刚度矩阵。

笔者利用黑油模型分析恒等温条件下油相的单相渗流。在均质和各向同性的油藏中，油相的运动方程为：

(5)

式中：v为流速,m/s；K为渗透率,mD；dp为压力增量,MPa；dL为长度增量,m；μ为黏度,mPa·s。

在恒温条件下，从质量守恒原理出发可得到流体的质量守恒方程为：

(6)

式中：ρ为密度,g/cm3；φ为孔隙度,1;t为时间,s;vx、vx、vx分别为x、y、z方向上的流速,m/s。

出砂是岩石在流体和应力作用下超过自身破坏极限的一种应力释放过程，出砂是复杂的流固耦合过程，需要采用微分方程组求解。数值模拟方法一般分为有限单元法、有限差分法和离散元法等。有限单元法是使用单元将连续体进行离散化，通过对单元作插值进而求解各种力学问题。有限元法的优点是：①可以求解各种线性和非线性问题；②能满足各种复杂边界条件；③通过前处理和后处理技术的发展，实现可视化操作。

使用有限元方法进行求解，Mohr-Coulomb准则的塑性屈服面方程为：

F=Rmcq-ptanφ-c=0

(7)

(8)

(9)

式中：F为体积力，MPa；φ为q-p应力面Mohr-Coulomb屈服面的倾斜角，通常称作材料的内摩擦角,(°)；c为材料的黏聚力,MPa；Rmc为屈服面形状因子,1；p为正应力,MPa；q为剪应力,MPa;θ为极偏角,(°)；J3为第三应力偏量不变量,MPa。

因为Mohr-Coulomb屈服面存在尖角，如果采用相关联的流动法则，在尖角处会出现塑性流动方向不唯一的现象，引起计算缓慢和收敛困难。因此定义塑性势面为连续光滑的椭圆函数:

(10)

式中：G为塑性势函数，Pa;ε为子午面上的偏心率,1;α为剪涨角，(°);c0为初始黏聚力,MPa，即未出现塑性应变时的黏聚力。偏心率控制着塑性势函数G在子午面上的形状与函数渐进性之间的相似度。

通过有限单元法可以实现岩石屈服面大小的变化，进而对中等强度砂岩的应力状态及出砂机理进行计算。

2 岩石井周应力计算

储层岩石在地下受到地应力、孔隙压力及井筒流体压力的影响，处于一个复杂的应力状态。钻井时井眼岩石移除，井壁围岩的应力重新分布，采油时井底流压逐渐降低改变了渗流场的分布。应力场及渗流场的耦合作用决定了储层岩石的破坏形式。

为模拟不同应力状态、生产制度及储层物性对出砂的影响，取表2所示的渤海湾某油田沙河街组油藏的储层物性参数作为模拟的基本条件。

表2 计算模型基础参数

砂岩在复杂的应力条件下，在井壁上某点的应力状态达到Mohr圆后岩石发生屈服进入塑性状态。岩石进入塑性屈服后，井壁岩石的应力分布与岩石性质、井筒液柱压力等有关，这与弹性阶段的应力分布有所不同。随着井底流压不断降低，井眼周围的塑性区形状和面积也不断发生变化。

由于受到地质沉积的影响，大多数情况下水平构造应力是不相等的。因此在钻井及采油过程中井眼进入塑性后，塑性区形状不是圆形。使用有限元数值模拟软件进行非线性耦合求解，得到了不同井底流压条件下的塑性区扩展规律。

图1为井底流压16、12、8MPa时井筒塑性变形区的模拟结果，其中X轴方向为最小主应力方向，Y轴为最大主应力方向。从图1可以看出，在最小主应力方向(X轴方向)井眼率先开始进入塑性变形，在生产时最小主应力方向是出砂的危险区域。塑性区成椭圆状，长轴位于最小主应力方向，随着生产压差的增大，塑性区逐渐扩展，最终整个井眼全部进入塑性区。

根据Mohr-Coulomb准则在地层生产条件下，井壁岩石的应力状态达到屈服点后进入塑性状态。岩石在塑性状态的应力分布与弹性状态有很大的区别。由于井底流压降低，近井筒岩石已进入塑性区，远场仍处于弹性区。从图2中不同距离处的径向应力对比可以看出，塑性区内岩石的径向应力明显小于弹性区。在弹性区域内最大主应力方向上，径向应力出现条状分布规律，最大水平地应力方向的径向应力明显高于最小水平地应力方向的。井眼附近岩石由于已进入塑性状态，其径向应力降低，且越靠近井眼径向应力越低。

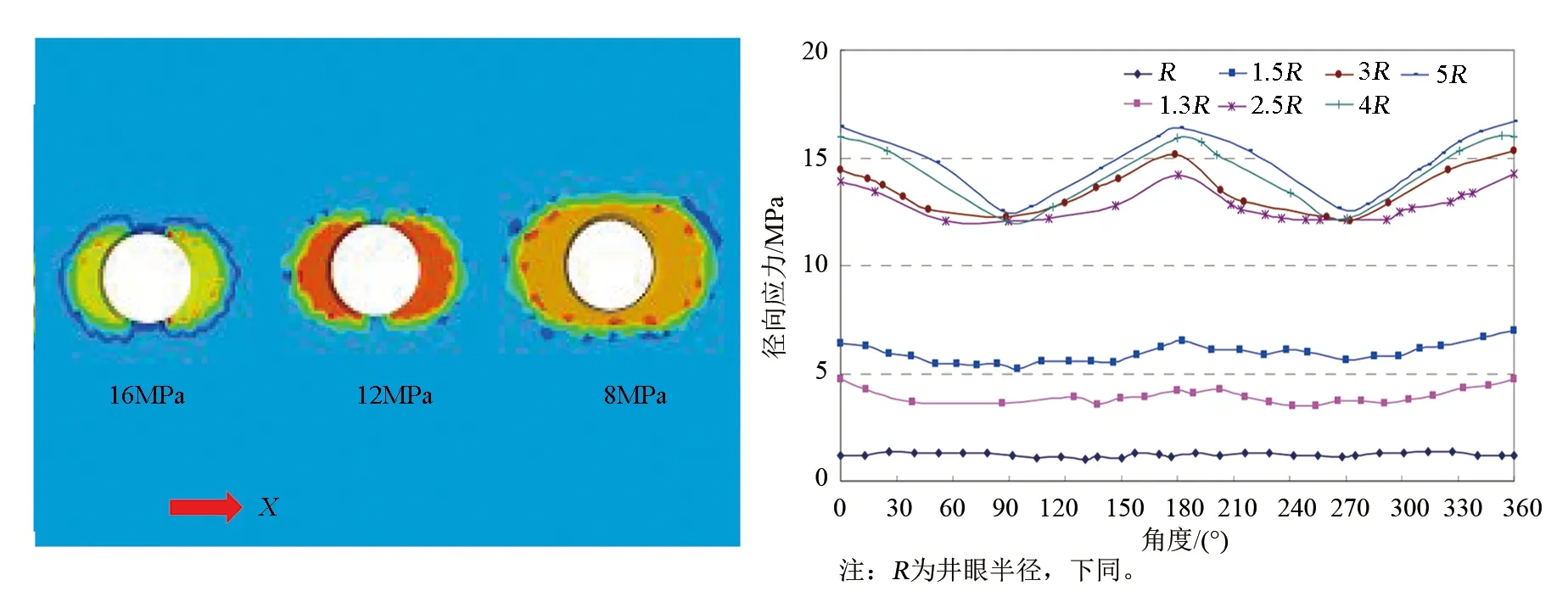
图1 不同井底流压条件下井筒变形模拟 图2 不同距离处井眼周围径向应力分布

根据线弹性理论，在井壁上最大的切向应力出现在与最大主应力夹角90°方向，且随着距离的增大，切向应力逐渐降低并趋于稳定。由于岩石受地应力及孔隙压力的影响，近井地带发生屈服，岩石在进入塑性阶段后其承载能力下降。根据数值模拟结果(见图3和图4)，可以看出切向应力在弹性区内，越靠近井眼，切向应力越大。但在塑性区出现反常，切向应力在塑性区内，越靠近井眼，切向应力越小，井壁处切向应力最小。

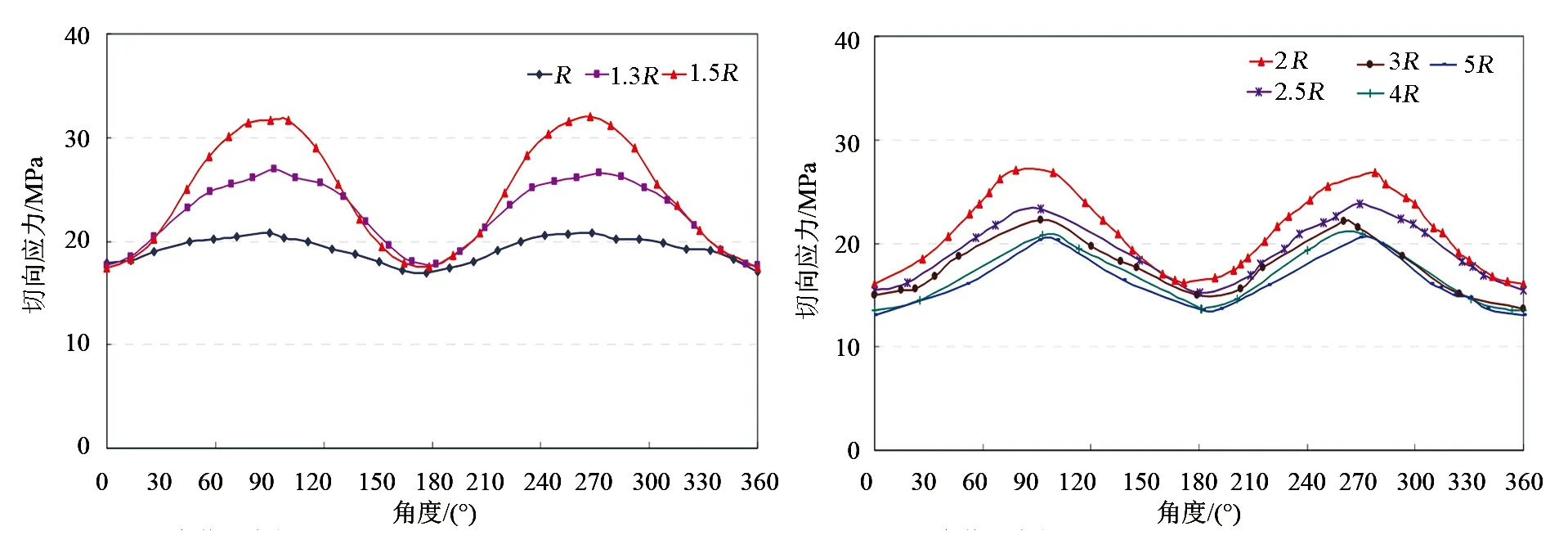
图3 不同距离处塑性区切向应力分布 图4 不同距离处弹性区切向应力分布

3 出砂时机预测

通过对不同地应力条件的塑性区扩展规律及井周应力分布规律的研究，可以发现随着井底流压的降低，近井地带的岩石在应力作用下进入屈服，极大地降低了岩石的承载能力，岩石颗粒之间的胶结力下降。生产过程中，由于流体的流动产生巨大的拖曳力。在流体拖曳力的作用下，岩石颗粒间胶结力弱的部位就产生出砂。

H.Kjorholt等认为,等效塑性应变超过一定值后岩石颗粒之间的胶结会断开形成游离砂，并在流体作用下产出。H.Kjorholt定义等效塑性应变为：

(11)

式中：εp为等效塑性应变,1；εp1、εp2、εp3为3个主应力方向的塑性应变,1。

图5 不同井底流压下井壁处不同位置的等效塑性应变

计算不同压差下井筒等效塑性应变，结果如图5所示。当井底流压降低到17.89MPa时，井眼区域开始出现等效塑性应变大于0.003的区域，油井游离砂在流体作用下率先产出，形成轻微出砂。当井筒内压继续降低至13.89MPa时，井筒周围岩石全部产生塑性变形，最大塑性应变0.0042。井底流压降低至11.15MPa，井壁岩石的等效塑性应变超过0.0048，此时井壁岩石会发生大规模的脱落，造成严重的出砂。生产压差越大，出砂越严重。

实际生产表明，井底流压13MPa时，井口无出砂，该生产压差下最大塑性应变0.0045。计算结果与现场监测结果一致，较好地指导了现场完井防砂的选择。因此,裸眼或套管射孔炮眼出砂的判别依据为等效塑性应变不超过0.0045，否则应采取防砂措施。

4 结论

1)建立了砂岩多孔介质变形破坏的弹塑性本构方程，采用Mohr-Coulomb准则作为初始屈服条件，后续屈服条件随塑性变形的发展而不断变化。推导了中等强度砂岩单相渗流的渗流场方程，建立了岩石应力场与流体渗流场相耦合的流固耦合模型。

2)使用有限元方法对出砂过程中的井壁岩石塑性区扩展进行了模拟。非均匀地应力条件塑性区最先在最小地应力方向出现，随着井底流压的降低，塑性区逐渐扩展，并最终呈现椭圆状。

3)近井地带的岩石受地应力及孔隙压力的影响会发生屈服进入塑性阶段，与弹性理论相对比可以发现，由于塑性的影响井周应力发生了变化，特别是切向应力严重降低，井壁上的切向应力降为最小。

4)采用等效塑性应变作为出砂判别依据，当等效塑性应变超过0.0045后岩石骨架砂开始大规模产出。计算结果与现场监测结果一致，为现场完井防砂方式的选择提供了理论依据。