围压作用下裂隙岩体变形破坏及碎胀特性研究

袁树成

(中铁十四局集团第二工程有限公司 山东泰安 271000)

1 引言

在巷道的施工过程中，围岩常发生威胁工程安全的有害变形[1-2]，围岩支护是减小有害变形的常用有效手段。对于存在破裂带的巷道围岩，已有研究证明裂隙倾角影响裂隙岩体的力学行为，巷道围岩的支护对象是具有复杂力学行为的裂隙岩体[3-4]。因此，研究不同围压条件下裂隙岩石变形破坏及碎胀特性对确保巷道围岩稳定性至关重要。

室内试验是研究岩石力学行为的重要手段，刘洪磊等[5]结合声发射监测技术开展了岩石试样的单轴压缩试验，分析了试块受力破坏时的声发射规律，研究了单轴压缩条件下岩石的强度特性及破坏模式。向天兵等[6]通过开展裂隙岩石的真三轴试验，分析了三向应力条件下结构面对岩体的稳定性的控制效应，研究指出岩体的破坏模式及支护效果与结构面参数息息相关。刘刚等[7]利用真三轴巷道平面应变模型试验，研究了节理密度对深埋裂隙岩体破裂区及碎胀变形的影响。TIWARI等[8]为了充分研究裂隙岩石的峰后失稳行为，相继开展了常规三轴试验与真三轴试验，研究了裂隙几何形状及加载方式对岩石强度及变形破坏的影响，提出了在准三轴和真三轴应力条件下估算峰后模量的表达式，建立了岩石硬化、软化、弹塑性变形的评估方法。Kulatilake[9]、Sagong[10]、Wang[11]等人则是将室内试验与数值分析方法相结合，分别研究了单轴、三轴条件下裂隙岩体裂纹发展规律。通过试验的方法得到岩石的力学性质后，要建立本构模型才能将变形规律广泛地应用到实际工程中，国内外的许多学者都做过岩石本构模型方面的研究。张强等[12]针对深部岩体，引入中间主应力，基于统一强度理论建立了弹塑脆性模型，通过解析的方法获得了围岩应力场及变形场。卢兴利[13]、黄兴[14]等人依托室内岩石三轴卸荷试验，分析了不同围压条件下完整岩石各特征应力值的演化特性，提出了岩石发生峰后碎胀变形的判别准则，建立了考虑岩石扩容碎胀演化机制的本构模型，并通过数值软件实现了本构模型的工程应用，但并未考虑裂隙的影响。Gao等[15]则认为在岩石破坏不可避免时，应当重点关注岩体的残余强度，特别是对于预先存在裂隙的岩体，其借助离散元软件分析了围压对岩体峰值强度及残余强度的影响，并提出了提高岩体残余强度的支护方法。

以上研究主要集中在围压或裂隙对岩体力学特性的单一影响上，考虑裂隙倾角及围压共同影响的研究比较少，特别是针对裂隙及围压对岩体峰后碎胀变形影响的文献还很少见。本文开展了不同裂隙倾角的类砂岩常规三轴压缩试验，分析了裂隙倾角及围压对试块强度特性的影响，提出了裂隙岩体峰后碎胀变形模型，研究了围压及裂隙倾角共同影响下裂隙岩体的碎胀变形特性。研究成果为巷道等地下工程的围岩支护设计提供一定的理论依据。

2 试验设计

本次试验试样采用含预制裂隙的标准圆柱形(高为100 mm，直径为50 mm)类砂岩试件。预制裂隙的倾角分别为15°、30°、45°、60°、75°，如图1所示。

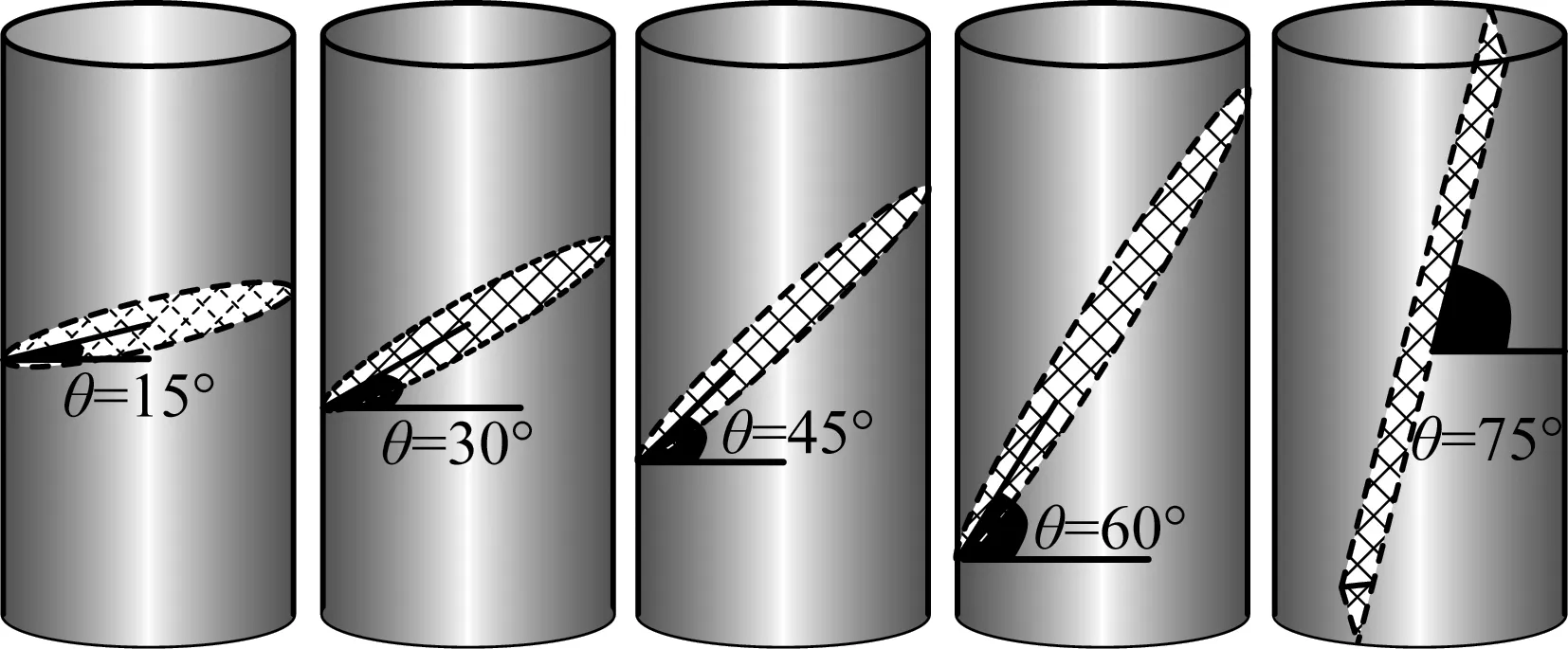
图1 含贯穿节理的岩石试件

试件采用425#普通硅酸盐水泥、砂子、水、早强减水剂按照1∶2.8∶0.36∶0.02的比例进行配比，试块力学参数满足砂岩相似度要求[16]645-646，表1为试块与砂岩物理力学参数的对比结果。对于裂隙的模拟，本文在对比分析不同的裂隙制作方法后，选用硬纸条编成的网状结构模拟裂隙[17]，硬纸条宽1 cm(见图2)，图中空隙部分允许透过上述水泥砂子混合液。试块制作过程为：按比例配置材料→搅拌机搅拌均匀→将均匀的混合料倒入模具中→振动去泡→养护24 h后拆模→标准养护28 d→取芯→打磨端部。

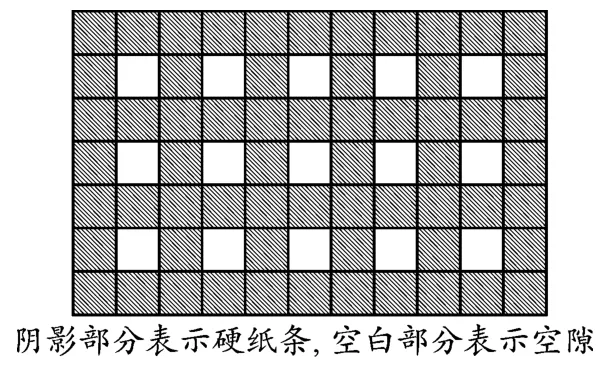
图2 模拟裂隙的网状结构

表1 试块与砂岩的力学参数对比

本次试验采用的试验设备为RLW-1000型岩石三轴流变仪。试块的轴向应变与径向应变分别采用轴向位移传感器与径向位移传感器进行测量，而后根据应变的定义计算得到相对应的应变。定围压为2、5、7、10 MPa，加载速率为200 N/s；轴压以0.5 mm/min的加载速率加载到岩石试件完全破坏为止。试验时对每个裂隙倾角试件，进行相同试验条件下的重复试验，每个系列重复3次，选取平均值作为该角度的试验结果。

3 试验结果分析

3.1 围压及裂隙倾角对岩石强度的影响

通过常规三轴试验得到不同围压下裂隙岩石的应力应变曲线，如图3所示。从图3a中可以看出：裂隙倾角15°的试块峰值强度最大，裂隙倾角75°的试块峰值强度最小；裂隙倾角由30°增大到45°时，其应力-应变曲线差别最大，其峰值强度及残余强度均显著减小。从图3b中可以看出：峰值强度与残余强度最大的仍是含15°倾角裂隙的试块；但当裂隙倾角超过60°时，其峰值强度、残余强度的减小趋势减弱。从图3c中可以看出：当裂隙倾角小于等于60°时，裂隙倾角对其峰值强度及残余强度的影响较大，但整体上试块的峰值强度及残余强度均随着裂隙倾角的增大而减小。从图3d中可以看出：10 MPa围压条件下，试块峰值强度及残余强度随着裂隙倾角的变化趋势与2、5、7 MPa围压条件下相同，均是随着裂隙倾角的增加而减小；但对于具有相同倾角裂隙的试块，10 MPa时的峰值强度＞7 MPa时的峰值强度＞5 MPa时的峰值强度＞2 MPa时的峰值强度，10 MPa时残余强度＞7 MPa时残余强度＞5 MPa时残余强度＞2 MPa时残余强度。

综上所述：一定围压条件下，预制节理倾角越大，裂隙试块的峰值强度及残余强度越小；不同裂隙倾角试块应力应变曲线峰前阶段的形状基本相似，裂隙倾角主要影响裂隙试块应力应变曲线的峰后部分；在一定节理倾角下，试块的峰值强度及残余强度随着围压的增加而增大；低围压状态下试块的峰后塑性变形小于高围压状态下的试块峰后塑性变形，即随着围压的增大试块的峰后塑性增强。

图3 不同围压条件下不同裂隙倾角岩样的应力-应变曲线

表2为不同裂隙倾角及围压下试块的峰值强度值及残余强度值。根据表中数据，分别得到峰值强度和残余强度与围压及裂隙倾角的相关关系，其拟合关系如式(1)所示。从式中可以看出，裂隙试块的峰值强度及残余强度受裂隙倾角与围压的共同影响。

式中，σf为试件峰值强度；σc为试件残余强度；σ3为围压值；θ为预制裂隙倾角；R为拟合相关系数。

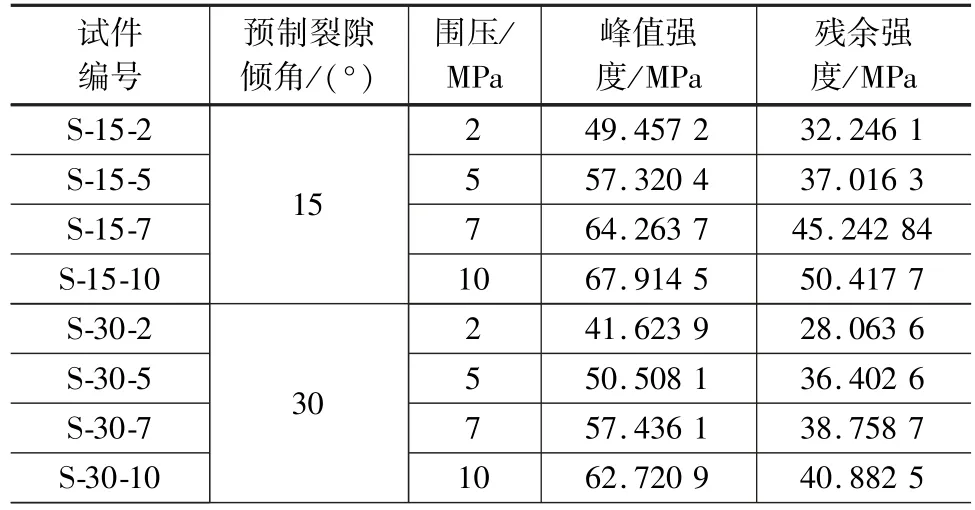
表2 试样强度

续表2

3.2 围压及裂隙倾角对体积应变的影响

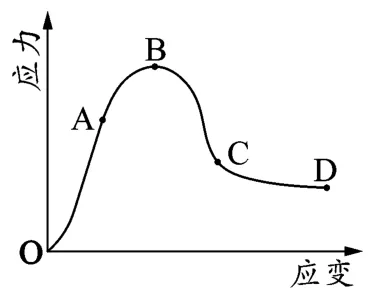
图4 裂隙岩石一般应力-应变曲线

根据上述试验得到的裂隙岩石应力-应变曲线的变化趋势，可将不同围压条件下裂隙岩石应力-应变曲线分为以下4个阶段(见图4)。OA段：此阶段初始阶段内部微裂纹被压密，试块体积略微减小，随着应力的不断增加，试块发生可恢复的弹性变形，而后试块由单纯的弹性变形转化为弹塑性混合变形，A点即为弹性变形转为弹塑性混合变形的临界点。AB段：试块发生弹塑性变形，试块内部裂纹不断发展，造成试块体积膨胀，产生损失扩容；当达到B点时，试块内部微裂纹逐渐贯穿，但并未出现滑移扩张。BC段：峰值强度后，试块内部裂纹进一步扩展，并大量贯通，导致试块产生初期碎胀变形；断裂能逐渐降低为零，试块体内的弹性能转化为动能，表现为破裂缝的扩张。CD段：此阶段的应力较低，破裂块体在低应力作用下，沿破坏面滑移、转动，产生较大的体积膨胀，试块结构破坏。

根据岩石体积应变的定义εν＝ε1+ε2+ε3[18]，围压条件下ε2＝ε3，则由试验测得的试块轴向应变、径向应变可得到其体积应变。表3为部分试样的轴向应变、径向应变，计算整理后体积应变如图5、图6所示。图5为裂隙倾角为30°的试块在不同围压条件下的体积应变。从图5中可以看出，峰后的碎胀变形远大于峰前的弹塑性变形，约占总体积应变的90%左右；围压越大，裂隙试块峰后碎胀变形越小，但围压对峰前弹塑性变形的影响并不明显，即围压对控制试块的碎胀变形更有效。图6为7 MPa围压条件下不同裂隙倾角试块的体积应变。由图6可知，裂隙倾角对峰前弹塑性变形的影响程度高于围压对峰前变形的影响程度；裂隙倾角对峰后碎胀变形的影响基本表现为裂隙倾角越大峰后碎胀变形量越小，但规律并不唯一，可能与试块破坏模式有关。

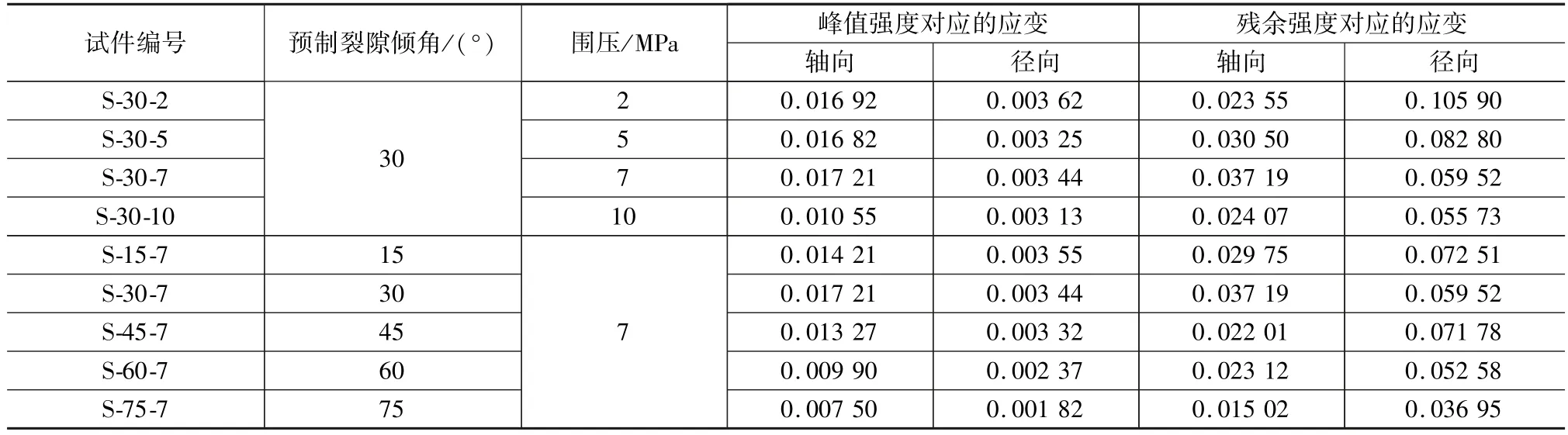
表3 试样应变

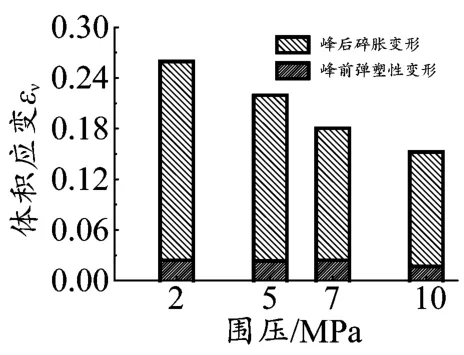
图5 不同围岩下的体积应变

图6 不同裂隙倾角体积应变

4 裂隙岩体碎胀变形模型

4.1 碎胀变形模型的建立

巷道支护的主要作用是限制松动圈内碎裂岩体在发展过程中产生过大的有害变形[19]58。由于松动圈内围岩处于破裂状态，原有的以弹塑性为基础的数学模型在此无法直接引用和借鉴。根据围岩松动圈内位移的传递规律[19]56-57，裂隙岩体碎胀应变可以用图7来描述，其数学表达式为：

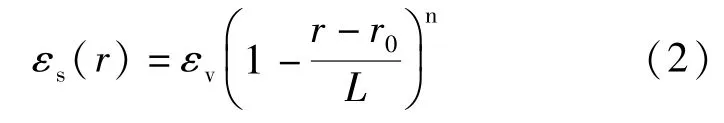
式中，εs是指碎胀应变；εv指松动圈表面的碎胀应变，即试验测得的体积应变；r0为巷道半径；L为松动圈的厚度；n是指与岩石性质有关的曲线形状因子，n＝0时εs为常数，n＝1时εs为一条直线，n越大说明岩石强度越高。

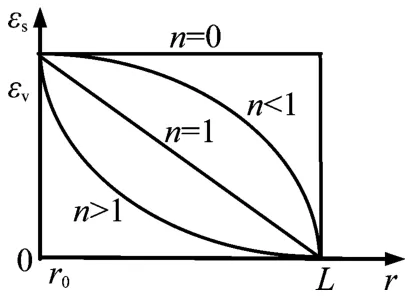
图7 εs与L的关系曲线

巷道周边的裂隙岩体碎胀应变产生碎胀变形，造成碎胀压力。假定r处碎胀应变引起巷道周边裂隙岩体径向碎胀变形的增量为dus，则

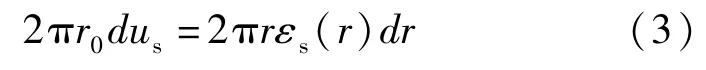
对于某一具体的工程，n、r0为常数，则公式(4)积分得碎胀变形us为：

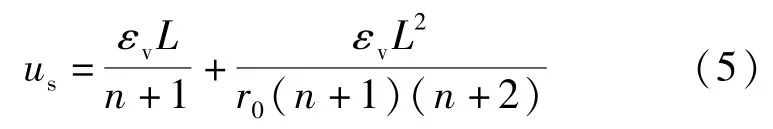
结合3.2节及式(5)分析可知围压越大，εv越小，碎胀变形越小。

巷道开挖后，岩体应力重新分布，由于应力集中，围岩周围形成松动圈，巷道周边岩体应力逐渐下降至残余应力。已有研究证明，残余强度对控制松动圈的进一步发展至关重要[16]649，也就是说，可通过提高岩体的残余强度来控制巷道周边裂隙岩体的应变，支护主要是要控制岩石峰后残余强度阶段的变形。基于3.1节中裂隙岩石残余强度与围压及倾角的关系，得到含裂隙的巷道围岩松动圈发展变化规律[20]：

式中，L为松动圈的厚度；P0为原岩应力；σ3为围压即支护力；θ为裂隙倾角；对于某一具体的工程，a、b为常数。

将公式(6)代入式(5)，整理得：

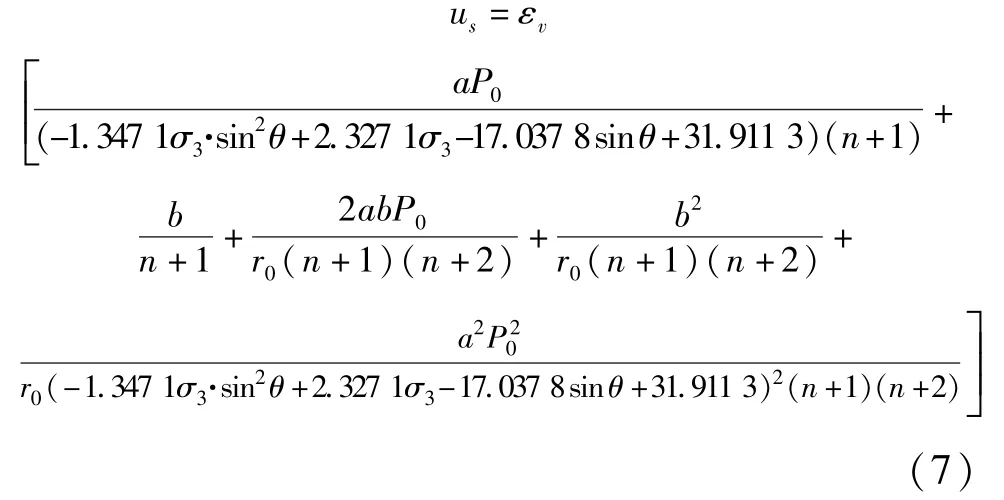
从上式可知，裂隙倾角与围压共同影响着裂隙岩体的碎胀变形。在实际工程中应针对不同的裂隙岩体设置适当的支护力(及时支护)来抵抗围岩碎胀力，抑制围岩的体积应变，控制围岩碎胀变形，从而防止巷道周边裂隙岩体过分变形发展造成工程事故。

4.2 碎胀变形模型的验证

为了验证上述模型的可行性，采用FLAC3D进行数值模拟试验。计算模型如图8所示，高宽厚均30 m，裂隙倾角分别为30°、75°，简化后的巷道断面直径为5 m。物理力学参数如表1所示，裂隙的参数是将岩体参数弱化1 000倍。上表面为自由边界，其余表面采用法向固定约束，模型顶部施加应力16.464 MPa用于补偿高埋深产生的原岩地应力。

图8 计算模型

图9为不同支护力作用下巷道周围竖向位移分布云图，图中的σ3为围压即支护力，θ为裂隙倾角。从图中可以看出：相同裂隙倾角下，提高支护力能有效控制围岩变形；相同支护条件下，θ＝45°时巷道围岩变形大于θ＝30°时的变形。选取数值模拟中巷道顶部竖向位移与本文碎胀变形理论模型对比，结果如图10所示。由图10可知，理论计算结果和数值模拟结果基本一致，验证了上述碎胀变形模型的正确性。

图9 巷道周围竖向位移

图10 计算结果对比

5 结论

(1)开展了不同裂隙倾角的裂隙岩石常规三轴压缩试验，获得了不同围压条件下裂隙岩石变形破坏规律及碎胀特性，建立了裂隙岩体峰后碎胀变形模型，并通过数值试验验证了模型的可行性。

(2)围压越大，裂隙岩石的峰值强度、残余强度越大；裂隙倾角越大，裂隙岩石的峰值强度、残余强度越小。裂隙岩石峰值强度之前主要发生弹塑性变形，峰值强度之后裂隙岩石主要发生碎胀变形。围压主要影响裂隙岩石的峰后碎胀变形，围压越大，岩石的峰后碎胀变形越小。

(3)裂隙倾角与围压共同影响着裂隙岩石变形破坏规律及碎胀特性。在含裂隙的巷道围岩支护设计施工中应充分考虑围压及裂隙倾角对围岩稳定性的影响。对于裂隙数目对巷道围岩峰后体积膨胀的影响将在后续研究中开展。