带有Lévy跳与饱和项的 随机互惠种群模型的渐近行为

赵晓丹,赵爱民, 刘桂荣

(山西大学 数学科学学院, 山西 太原 030006)

0 引言

在生态系统中, 物种的互惠现象是非常普遍的. 为此, 国内外许多学者建立了不同的互惠种群模型, 并利用微分方程定性理论分析了种群动力学行为[1]. 随着社会的快速发展, 环境污染日益严重, 对生物种群的生存带来极大的危害. 从而在建立种群动力学模型时, 很多学者考虑了环境毒素的影响[2-3].

此外, 种群的生存还受环境噪声的影响. 因此, 利用随机微分方程刻画种群动力学行为更符合实际. 为此, 文献[4]建立了下列具有饱和项和毒素影响的随机互惠种群系统研究了系统(1)的灭绝性与持久性.

(1)

另一方面, 一些突发的且严重的环境扰动现象会对生态种群的数量产生巨大的影响, 如地震、飓风、海啸、传染病等. 近年来, 一些学者用Lévy跳来描述这些不连续的随机扰动现象[5]. 基于上述研究动态, 本文考虑了下列带有Lévy跳与饱和项的随机互惠种群模型

(2)

1 全局正解的存在唯一性

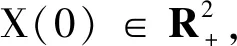
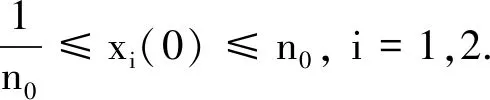
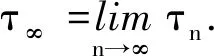
假设τ∞≠∞ a.s. 则存在常数T>0与ε∈(0,1), 使得

P{τ∞≤T}>ε.

(3)

即存在n1≥n0, 使得对所有的n≥n1, 有P{τn≤T}≥ε.

(4)

其中

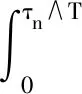
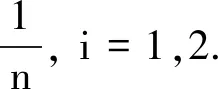
其中IΩn为Ωn的示性函数. 从而

这是一个矛盾. 从而,τ∞=∞, a.s. 定理1得证.

当γ1=γ2=0时, 定理1仍成立, 与文献[4]中定理3.2.1结论一致.

2 灭绝性

在研究生态系统的性质中, 灭绝性也是一个很重要的性质. 接下来, 我们考虑系统(2)的灭绝性.

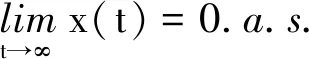
首先, 根据文献[6]引入一个引理.

引理1 设z∈C(Ω×[0,+∞),R+), 若存在常数T>0,λ0>0,λ,σi与λi,(i=1,2,…,n)使得对于所有t≥T, 有

则

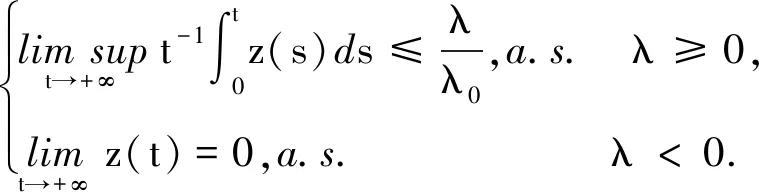
记:

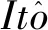
(5)

对(5)式两边从0到t积分得

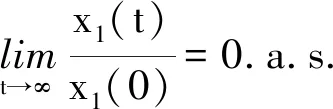
由于系统(2)为互惠种群系统, 种群x1与种群x2有对称性质. 类似的, 得到下述定理

根据定理2与定理3可得

3 数值仿真

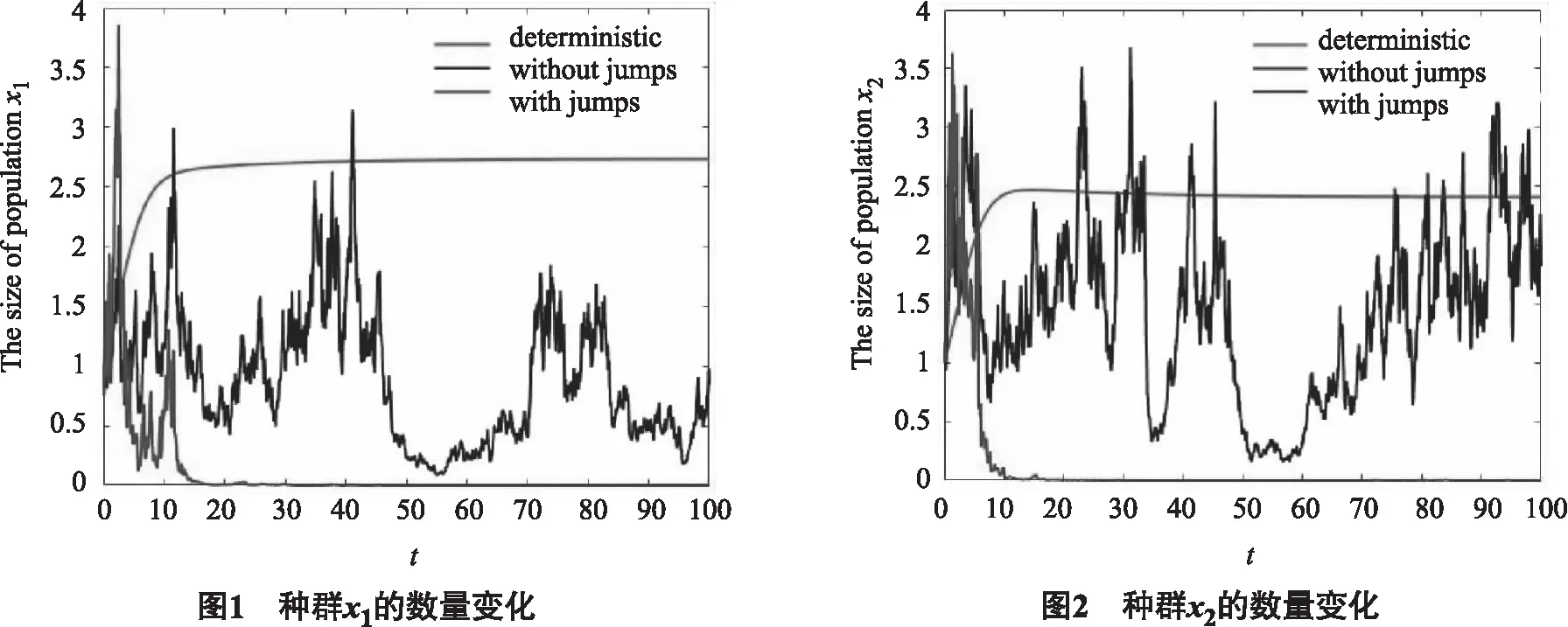
当γ1=0时,b1=0.174>0. 可以看出种群x1不受Lévy跳干扰时不灭绝. 当γ1=0.76时,b1=-0.020<0. 种群x1受Lévy跳干扰, 满足定理2的条件. 从而x1灭绝. 这与图1结果一致.

当γ2=0时,b2=0.175>0. 可以看出种群x2不受Lévy跳干扰时不灭绝. 当γ2=0.75时,b2=-0.015<0. 种群x2受Lévy跳干扰, 满足定理3的条件. 从而x2灭绝. 这与图2结果一致.

4 结论

本文讨论一类带有Lévy跳且具有饱和项的随机互惠种群模型. 通过构造合适的Lyapunov函数, 得到全局正解的存在唯一性. 利用It公式等随机微分方程基本理论, 得到种群x1,x2灭绝的充分条件. 通过数值仿真说明Lévy噪声不利于种群生存. 本文结果推广了文献[4]中的定理3.2.4.