基于负载匹配的阀控液压缸匹配特性研究
2019-05-21王鑫涛
王鑫涛, 杜 星
(中国飞机强度研究所全尺寸飞机结构静力/疲劳航空科技重点实验室, 陕西西安 710065)
引言
飞机结构强度试验是新机研制的主要环节之一,而阀控缸系统属于主要试验设备之一[1-2]。其中伺服阀的性能很大程度上决定了系统的性能,因此阀控缸系统的研究对于飞机结构强度试验有着相当重要的意义。试验中伺服阀一般采用双喷嘴挡板式反馈两级电液流量伺服阀,其先导级为对称的双喷嘴挡板阀,由干式双气隙力矩马达驱动,输出级为三位四通滑阀,阀芯位置由一悬臂弹簧杆进行机械反馈[3]。液压缸一般采用非对称缸,其结构简单,体积较小,承载能力大[4-6]。
目前在实际试验应用中,对于液压缸与伺服阀的选择基本上靠经验公式进行选取,这种方法存在着较大的偏差,伺服阀选择偏小,无法满足实际需要,伺服阀选择偏大,功率利用率较低,且伺服阀未工作在最佳状态,从节能的角度来说是一种浪费。对于强度试验而言,将影响其加载点阀控液压缸的控制性能和加载要求,某一个加载点的控制性能可能会对整个试验加载系统造成消极影响[7-8]。
1 负载特性分析
飞机结构强度试验中,试验件一般均属于弹性体,加载过程中存在一定的变形量。为保证试验件结构受力真实,试验时对于试验件的重量一般通过反配重进行扣除,保证试验件处于“0”状态,由于全机试验加载点较多,为保证每个加载点加载协调,液压缸运行速度通常较低,基本可近似认为匀速运动。因此液压缸所承受的负载力主要由弹性负载、粘性阻尼负载以及摩擦负载组成。
1) 弹性负载
弹性负载力:
FP=Kx
(1)
式中,K—— 试验件刚度,N/m
x—— 试验件变形,m
2) 粘性阻尼负载
粘性阻尼负载力:
FV=Bx′
(2)
式中,B—— 粘性阻尼系数,N·s/m
x′ —— 运行速度,m/s
3) 总负载力
运动过程中,动摩擦力Ff可认为一固定值,只发生方向上的变化[4]。
因此总负载力即为:
F=FV+FP+Ff=Bx′+Kx+Ff
(3)
采用频率法设计系统时,可以认为输入信号是正弦信号,负载是在作正弦响应,设负载力为:
F=Fmsinωt
(4)
式中,Fm—— 正弦运动振幅,N
ω—— 角频率,rad/s
则总负载力可表示为:
Fmsinωt=Bx′+Kx+Ff
(5)
由式(5)微分方程可以解得负载位移:
(6)
则负载速度:
(7)
将式(4)和式(7)联合则可以得到负载轨迹方程如下:
(8)
为更加直观的表示方程的几何特性,方程转化后也可表示为:
(9)
由图1可以看出,飞机结构强度试验中,其负载轨迹为一原点对称的斜椭圆方程。
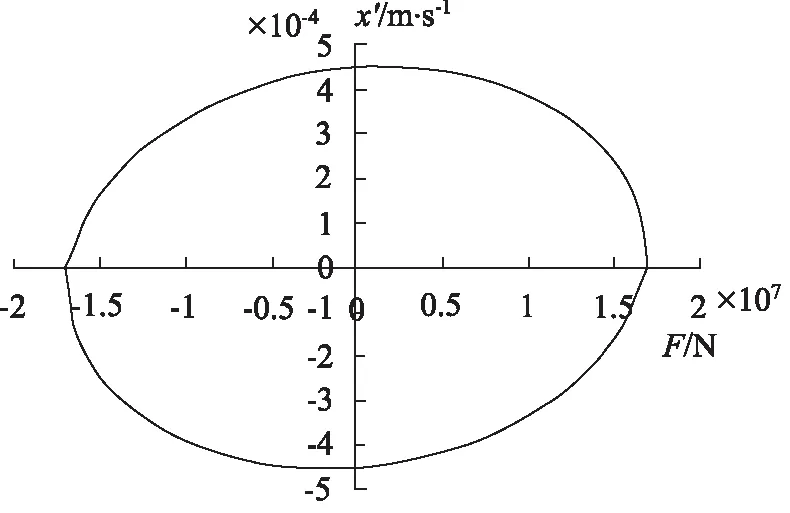
图1 负载轨迹
2 伺服阀压力-流量特性
为便于分析,认为实际使用的伺服阀为理想零开口四边滑阀,阀芯处于阀套中间位置时,4个控制节流口全部关闭。该滑阀节流阀口匹配且对称,其压力-流量方程一般表示为[9-14]:
(10)
式中,Cd—— 流量系数
A0—— 滑阀节流阀口面积,mm2
ρ—— 油液密度,kg/m3
ps—— 油源压力,MPa
xV—— 阀芯位移,mm
p—— 负载压力,MPa
我们仅讨论流量为正向的情况,即滑阀阀芯位移为正向,因此式(10)表示为:
(11)
一般在使用过程中,为便于用户使用,伺服阀提供的常规技术参数为阀口全开的情况下额定压降下的额定流量,根据伺服阀压力-流量特性方程,则额定流量与额定压降应满足如下关系:
(12)
式中,QN—— 伺服阀额定流量,m3/s
AN—— 滑阀全开节流阀口面积,mm2
ρ—— 油液密度,kg/m3
ΔpN—— 伺服阀额定压降,MPa
负载为空载情况下压降,即为油源压力ps。
由于讨论伺服阀与液压缸的匹配关系,必须保证伺服阀在最大输出的情况下满足负载特性需求,因此均以阀口全开的情况下进行研究分析[15],式(11)和式(12)联立可得:
(13)
实际强度试验中一般大部分采用MOOG生产的G761系列电液伺服阀,其给出的常规技术参数为7 MPa 额定压降下的额定流量,由于试验中液压泵的额定输出压力为21 MPa,通过液压子站输出的油液压力也为21 MPa,因此转换后其额定压力21 MPa时,伺服阀的额定流量如表1所示。

表1 伺服阀规格及参数
依据式(13)以及表1当中的伺服阀基本参数,可以做出5种伺服阀的压力-流量特性曲线,由于阀节流口对称,因此曲线应该对称于原点。为讨论方便,同样仅取流量为正的情况下,如图2所示。
3 伺服阀与液压缸匹配分析
本研究主要通过负载匹配来进行伺服阀的选择,选择的原则是伺服阀的流量-压力特性曲线要能够包围液压缸的负载特性曲线,同时两者之间的区域要尽可能小,如果伺服阀的最大输出功率点与负载的最大功率点重合,则认为两者是最佳匹配,此时功率利用率最好[16-17]。
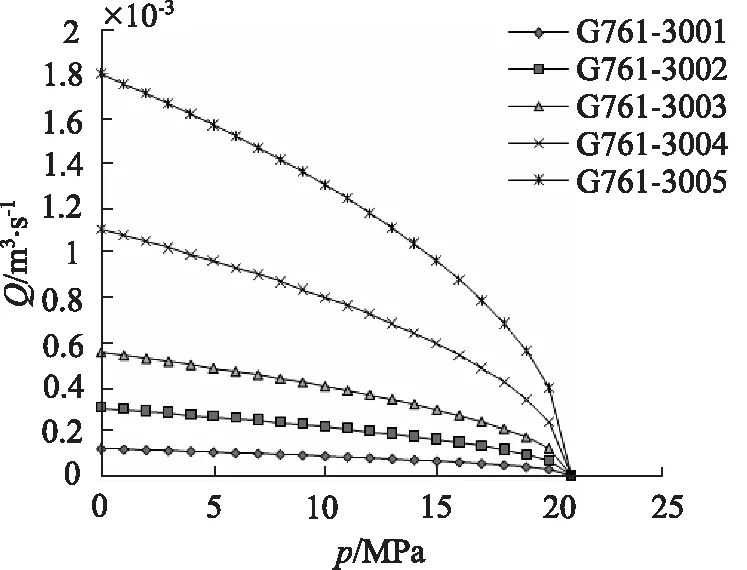
图2 伺服阀压力-流量特性曲线
实际应用中采用的液压缸种类较多,无法逐一进行列举,本研究仅以额定载荷10 t,行程1 m液压缸为例进行分析,由于一般采用液压缸为非对称缸,其额定载荷一般指有杆腔最大输出载荷。
通过负载匹配来进行伺服阀的选择可以在两种坐标系下进行分析,即负载力-速度坐标系和压力-流量坐标系。本研究选择在压力-流量坐标体系下进行分析,因此需要对负载轨迹方程进行转换。若液压缸有杆腔面积为A,则:
负载力:
F=p·A
(14)
负载速度:
(15)
代入负载轨迹方程式(8)和式(9)可得:
(16)
(17)
试验过程中加载点一般不止一个,为加快试验速率,必须保证每个点均能够较快的到达命令值,且加载特性良好。因此对于变形较大的区域,要使得其加载速率较快,必须使得负载流量较高。因此,试验件加载点的刚度直接决定着伺服阀的选择。
液压缸最大载荷10 t,行程为1 m,由于整个液压系统较为复杂,各个环节均会产生压力降,导致伺服阀入口压力很难达到21 MPa,且液压缸本身存在泄漏,通常情况下,液压缸实际载荷利用率不超过其最大载荷的80%为宜,因此试验件刚度最小临界值K=8×104N/m。试验加载时,至少要保证液压缸输出最大载荷的80%时能够满足加载要求,因此均以液压缸能输出的最大载荷80%进行分析。
图3表示2种不同试验件刚度下的负载轨迹,可以看出加载载荷相同的情况下,试验件刚度越大,其需要的流量就越小,因此,使用同规格液压缸的情况下,试验件的刚度直接影响着负载流量。
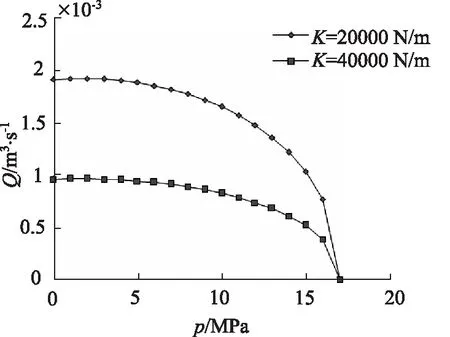
图3 不同刚度下的负载轨迹
由匹配原则得知,伺服阀的压力-流量特性曲线(见图4)刚好包围液压缸的负载特性曲线,此时两者为最佳匹配。从两者特性曲线来讲,即伺服阀压力-流量特性曲线刚好外切于液压缸的负载特性曲线,此时相切点(即最佳匹配点)处两者曲线斜率相等,因此最佳匹配点应满足如下条件:
(18)
若试验中系统加载角频率ω=0.1 rad/s,粘性阻力系数B=100 N·m/s,液压缸拉腔面积A=4760 mm2。通过式(18)可以得到10 t/1 m液压缸与5种不同伺服阀达到最佳匹配时的试验件刚度。
由式(18)解得:
K1=380233.2 N/m,K2=148290.5 N/m,
K3=80885.1 N/m,K4=40442.1 N/m,
K5=24714.2 N/m
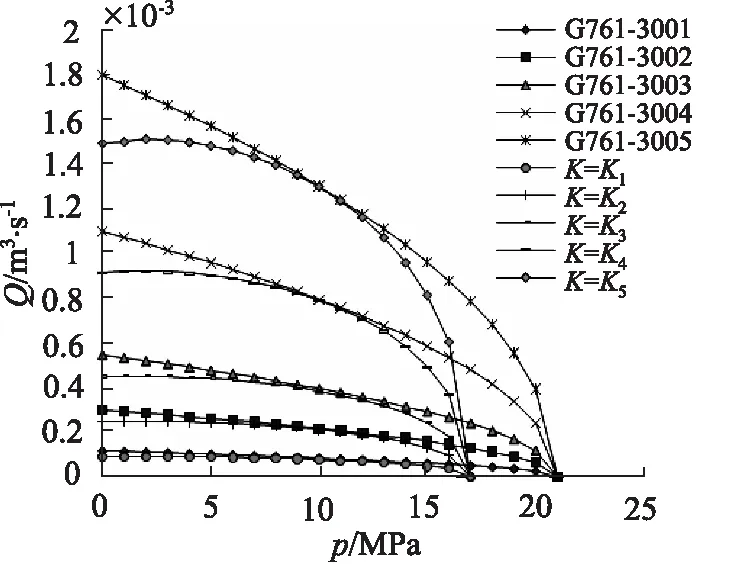
图4 伺服阀与液压缸匹配曲线
因此,要想伺服阀能够满足10 t/1 m液压缸输出负载需求,可参考如下条件。
当K≥K1时,采用3001阀;
当K2≤K 当K3≤K 当K4≤K 当K5≤K K 通过负载匹配的方法进行伺服阀的选择,能够让伺服阀尽可能的工作在最佳负载范围,继而提高伺服阀的使用效率,保证实际试验的加载精度以及加载效率。同时为类似特定加载系统的液压系统设计提供了参考依据,通过该方法能够保证伺服阀与液压缸进行合理匹配,功率利用率最好。4 结论
