气体减压阀动静压差研究

郭 珣， 樊 蕾

(北京航天发射技术研究所， 北京 100076)

引言

动静压差是气体减压阀在一定流量和进出口压力工况下，由动态切换到静态的出口压力变化量，是产品的一项主要性能指标。动静压差过大会对减压阀和气路系统产生不良影响。国家气动产品质量监督检验中心对国内部分气体减压阀进行了一系列测试[1]，得到产品动静压差实测值。姬俊锋、邓攀、彭育辉等在新阀的设计过程中，进行了关于流量的仿真，从其仿真结果中可得到动静压差[2-4]，但未对动静压差进行理论计算。

本研究对航天发射领域广泛应用的一种气控反向气体减压阀任意状态的静压和动静压差计算方法进行了理论和试验研究。

1 理论研究

1.1 机理分析

减压阀结构简图见图1。

根据气体一维恒定等熵流动基本方程[5]：

(1)

式中,p—— 气体压力

ρ—— 气体密度

u—— 气体流速

E—— 气体比内能

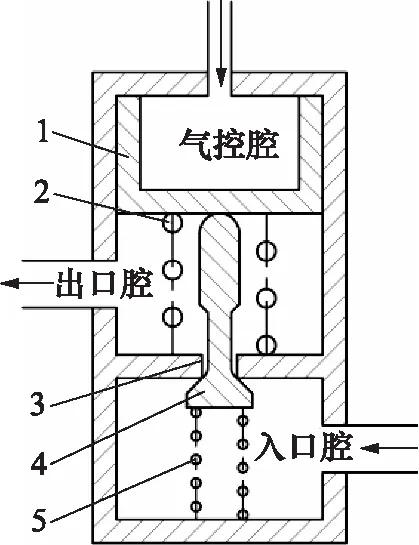
1.敏感活塞 2.敏感活塞复位弹簧 3.阀座 4.阀芯 5.阀芯复位弹簧图1 减压阀结构简图

气体开始流动时，部分压力能转化为动能，出口腔压力降低；敏感活塞在气动力作用下推动阀芯向下运动，气控腔容积增大，腔内压力下降， 力平衡状态改变，出口压力重新稳定，此时出口压力为动压。气体停止流动时，动能重新转化为压力能，出口腔压力回升；敏感活塞与阀芯复位，出口腔压力重新稳定，此时的出口压力为静压。静压与动压的差值称为动静压差。

1.2 理论计算

1) 静态工况受力分析

静态工况下阀芯受力分析见图2。

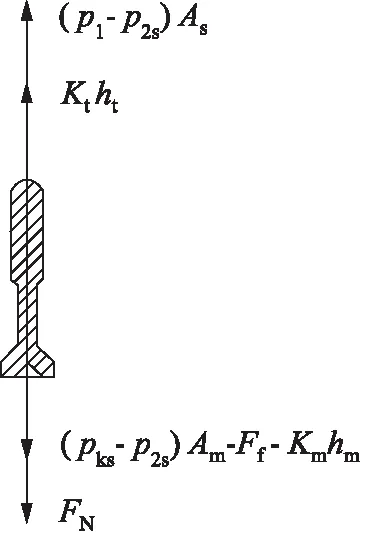
图2 静态工况阀芯受力

静态工况下阀芯受力平衡方程为：

(pks-p2s)Am-Ff-Kmhm+FN-Ktht-

(p1-p2s)As=0

(2)

式中,pks—— 静态工况气控腔压力

p2s—— 出口腔静态压力

Am—— 敏感活塞面积

Ff—— O形圈摩擦力

Km—— 敏感活塞复位弹簧刚度

hm—— 敏感活塞复位弹簧初始压缩量

FN—— 阀座对阀芯的反作用力

Kt—— 阀芯复位弹簧刚度

ht—— 阀芯复位弹簧初始压缩量

p1—— 入口腔静态压力

As—— 阀座孔面积

阀座与阀芯的理论最小密封比压由经验公式计算[6]：

(3)

式中,qmin—— 最小密封比压

C,K—— 与材料有关的常数

b—— 密封宽度

阀座对阀芯的反作用力为：

FN=Sπdsbqminsinα

(4)

式中,ds—— 阀座直径

S—— 密封系数

α—— 阀芯圆锥面母线与中心线夹角

2) 动态工况受力分析

假设气源压力稳定，动态工况下阀芯受力分析图见图3。

图3 动态工况阀芯受力

动态工况下阀芯受力平衡方程为：

(pkd-p2d)Am-Ff-Km(hm+x)-Kt(ht+x)-

(As-εA12)(p1-p2d)=0

(5)

式中,pkd—— 动态工况气控腔压力

p2d—— 出口腔动态压力

x—— 阀芯开度

ε—— 面积修正系数，取0.97[7]

A3—— 阀座节流面积

3) 流量计算

减压阀的流量由负载决定，负载模拟孔板流量计算公式为[8-9]：

(6)

式中,φx—— 孔板流量系数

Ax—— 孔板流通面积

R —— 气体常数

T—— 气体温度

k—— 气体绝热指数

p0—— 孔板出口压力

ycr—— 临界压力比

4) 阀芯开度计算

将气体在减压阀内流动近似认为是等温流动[10]，由此可得阀芯节流面积计算式为：

A3=Axyvrp

(7)

式中,yv—— 阀芯压比，yv=p2d/p1

rp—— 压比函数

压比函数可由式(6)得出，在不同压比组合情况下形式不同，见式(8)：

(8)

式中,yx为阀芯压比，y0=p0/p2d。

可得锥形阀芯开度x为：

(9)

5) 静压及动静压差计算

在减压阀工作压力为0～35 MPa，工作温度为常温，在此范围内压缩因子接近1[11]，所以将气体状态方程近似为理想气体状态方程：

pV=mRT

(10)

式中,p—— 容腔气体压力

V—— 容腔体积

m—— 容腔气体质量

忽略气控腔气体温度的变化，则由式(5)、式(9)、式(10)可得气控腔静态压力：

(11)

式中,V为气控腔初始容积。

将式(3)、式(4)、式(11)带入式(2)可以得到静压与动静压差计算公式为：

(12)

Δp2=p2s-p2d

(13)

式中, Δp2为动静压差。

2 影响因素分析

影响动静压差的因素主要有出口压力、气体流量、敏感活塞面积等。以某减压阀为例，进行动静压差影响因素的计算分析，相关参数见表1。

表1 减压阀部分参数

2.1 进出口压力

动静压差随着出口压力的升高而增大，且当进口压力增高时；动静压差增大的趋势减缓。进出口压力对动静压差的影响见图4。

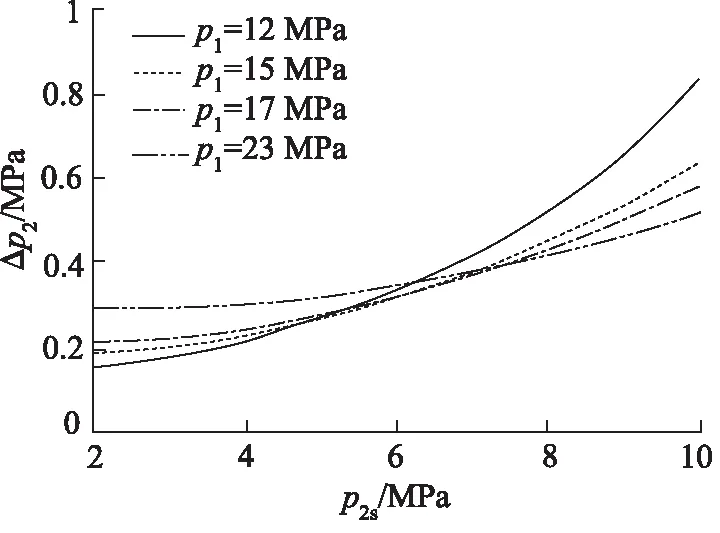
图4 进出口压力对动静压差的影响

根据图4可知，在进行气体减压阀结构参数设计时，一般对最高出口压力下的动静压差值进行计算。

2.2 气体流量

气体流量通过不同负载模拟孔板流通面积Ax来表示。动静压差随着流量的增加而增加。以进口压力为20 MPa时为例，气体流量对动静压差的影响见图5。

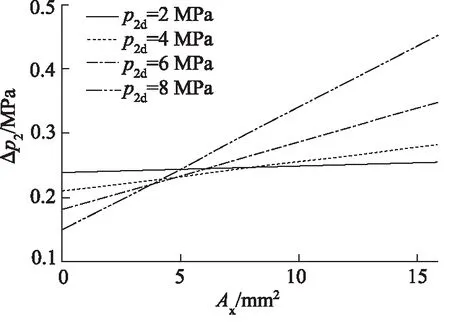
图5 气体流量对动静压差的影响

图中计算的Ax=0处，孔板处流量也为0，此处的动静压差，是阀芯刚刚接触阀座和阀芯完全密封所产生的压差。

根据图5可知，出口压力越高，动静压差随流量变化趋势越明显。在减压阀结构参数设计时，一般对最大流量时的动静压差进行计算。

2.3 敏感活塞面积

敏感活塞面积对动静压差的影响为“U”字形。以进口压力为20 MPa时为例，敏感活塞面积对动静压差的影响见图6。

根据图6可知，在不同出口压力下，动静压差最小值对应的敏感活塞面积不同，随着出口压力升高，动静压差最小值点左移。但存在一个敏感活塞面积的区间范围，使得动静压差均在一较小的范围内。在减压阀设计时应综合考虑使敏感活塞面积尽可能落在此范围内。

图6 敏感活塞面积对动静压差的影响

2.4 其他因素

经分析，其他一些因素如O形圈摩擦力、阀座孔面积等对动静压差影响较小，不再详细说明。

3 试验研究

试验气路如图7所示。试验过程中打开JF1、JF2，减压阀完成调压后，通过开关电磁阀DF进行动静压差的测试。通过P1读取减压阀进口压力，通过P2读取减压阀出口压力。

G.过滤器 JF1,JF2.手动截止阀 P1,P2.指针式压力表 JQ.减压阀 DF.电磁阀 X.负载模拟孔板图7 试验气路原理图

3.1 不同进出口压力试验

试验中负载模拟孔板面积为10.75 mm2，在不同进出口压力工况下进行测试。试验结果和式(12)计算结果见表 2。

表2 不同进出口压力试验静压计算结果 MPa

3.2 不同流量工况试验

入口压力为23 MPa，出口调节压力为10 MPa，选择不同的负载模拟孔板进行试验。试验结果和式(12)计算结果见表3。

表3 不同孔板流通面积试验静压计算结果

3.3 试验误差分析

表2、表3中静压计算值与试验值误差均小于5%，计算准确度较高。

静压试验值与计算值之间的误差来源有以下几方面：

(1) 经验常数、密封系数的选择；

(2) 测量方法和仪表精度的限制；

(3) 试验中气源压力存在微小波动。

4 结论

通过理论研究得出了一种气体减压阀任意状态静压和动静压差的计算方法，分析了动静压差的主要影响因素，并通过试验验证了计算公式的准确性。

本研究得到的计算分析方法可为气体减压阀产品研制和减压阀气路系统的设计提供技术途径。提出的研究方法也可在其他类型气体减压阀的动静压差分析时提供参考。