厚圆盘弯曲振动辐射声场指向性研究

张宁宁

(渭南师范学院数理学院，陕西 渭南 714099)

0 引 言

一般换能器的声阻抗远大于空气的声阻抗，所以应设计一种新型换能器满足其阻抗要求。复合弯振换能器可以使其声辐射效率和指向性得到明显提高，已经得到广泛应用[1-5]。文献[6-7]分别对阶梯圆盘弯曲振动辐射声场和辐射阻抗进行了比较详细的研究。目前对圆盘及阶梯圆盘弯曲振动特性及声场的研究相对比较成熟，但大多采用没有计入剪切形变影响的薄板理论，随着板的厚度增加，该理论的误差较大。指向性是描述声辐射体将声波辐射到各个方向的能力大小的一个物理量，是描述声场特性比较重要的物理量[8-9]，因此在实际应用中具有指向性的声辐射体被广泛使用。文献[10]对任意阵型的水声换能器的辐射声场进行研究，文献[11]对阶梯型圆盘复合换能器的指向性进行了系统的研究。在高频大功率声辐射条件下，经常需采用机械强度高、横向尺寸小的中厚盘[12-15]。目前对中厚盘的辐射声场指向性的研究不多，文献[16-17]利用有限元法对厚圆盘在不同边界条件下的基频弯曲振动辐射声场进行研究。为了进一步详细而全面地研究厚圆盘的辐射声场特性，本文在应用Mindin理论对厚圆盘的弯曲振动研究基础上[15]，推导出厚圆盘在三种不同边界条件下的弯曲振动辐射声场指向性的通用表达式，利用计算机编程对其声辐射特性进行详细研究，其结果对大功率弯曲振动辐射体的实际应用可提供一定的理论参考。

1 弯曲振动厚圆盘的频率方程

1.1 Mindin理论

假设厚圆盘的半径为a，厚度为h，上下表面不受切向力。根据Mindlin理论，有如下形式的质点位移[15]：

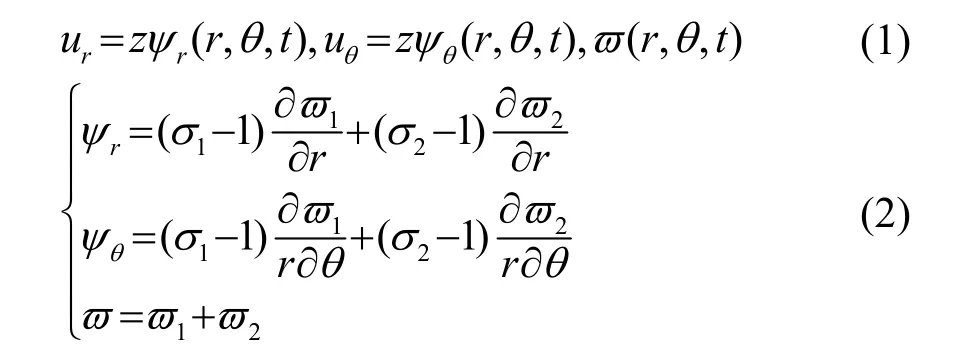
其中，ur、uθ、ϖ分别表示径向、切向、z向的位移。

弯矩和剪力分别为

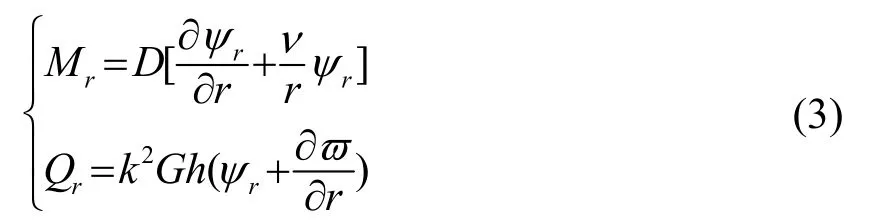
位移函数ϖ1、ϖ2分别满足：

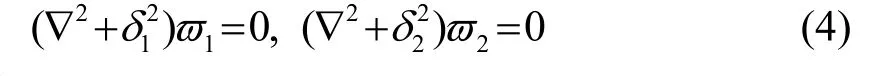
其中：

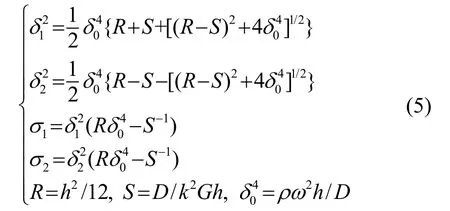
式中，D=Eh3/12(1-ν2)k2=π/12。ρ、ω、D分别为盘的密度、角频率、弯曲刚度常数，R、S分别为转动惯量和横向剪切变形的影响，ν为泊松比。当r=0时，圆盘的ϖ不能为无限大，由对称性可知ur(0,z)=0，弯矩Mr以及剪力Qr的表达式为

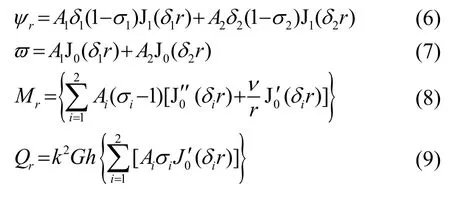
式中，J0(δir)，J1(δir)分别为为零阶、一阶贝塞尔函数，A1、A2是由边界条件决定的待定常数。

1.2 不同边界条件下厚圆盘的弯曲振动频率方程

自由边界条件下，圆盘边界处的弯矩和剪力为0，由式(8)、(9)可得[15]：

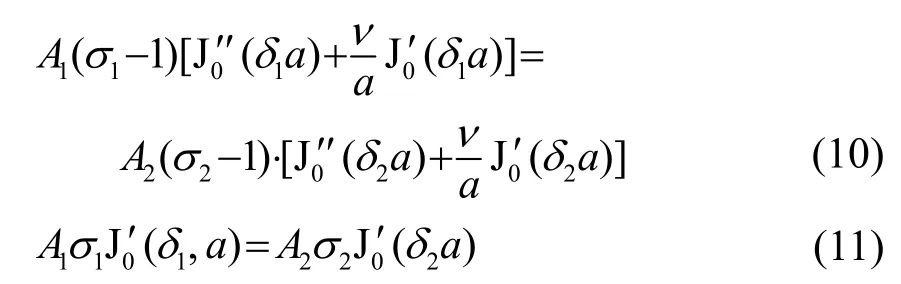
根据式(10)、(11)可确定系数A1、A2。将其代入式(7)即可得自由边界条件下圆盘的横向位移。根据式(10)、(11)可得厚圆盘在自由边界条件下的弯曲振动共振频率方程为

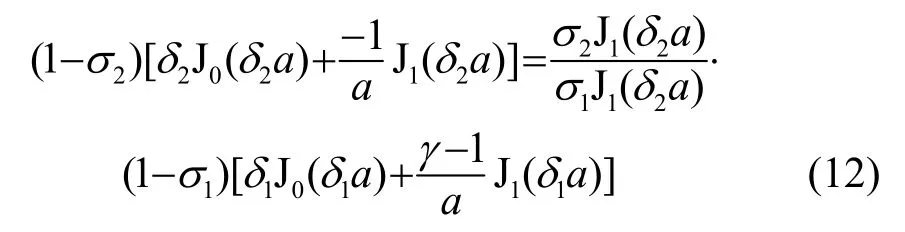
简支边界条件下，圆盘边界处的横向位移和弯矩为0，由式(7)、(8)可得：

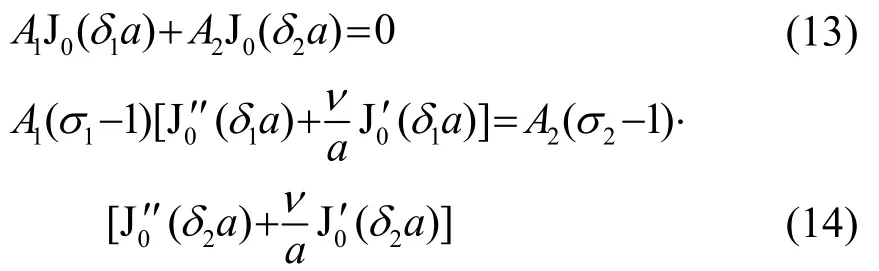
根据式(13)、(14)可确定系数A1、A2。将其代入式(7)即可得自由边界条件下圆盘的横向位移。根据式(13)、(14)可得简支边界条件可确定厚圆盘在简支边界条件下的弯曲振动共振频率方程为

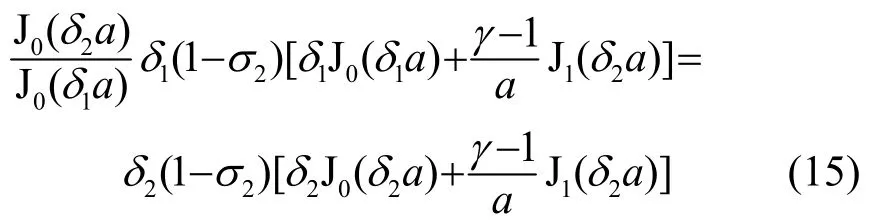
固定边界条件下，圆盘边界处的横向位移及其导数等于零，由式(7)可得：

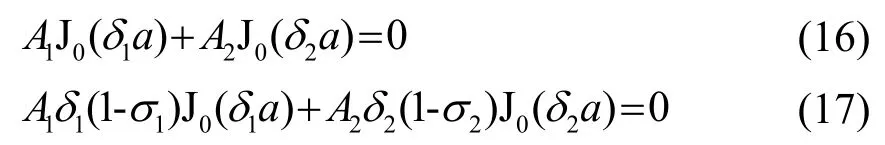
根据式(16)、(17)可确定系数A1、A2。将其代入式(7)即可得自由边界条件下圆盘的横向位移。根据式(16)、(17)可确定厚圆盘在固定边界条件下的弯曲振动共振频率方程为

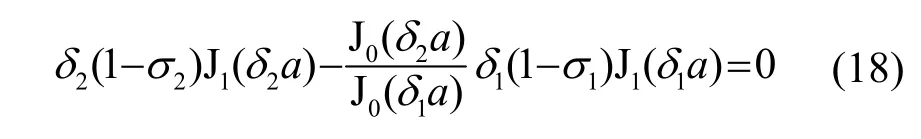
由频率方程(12)、(15)、(18)可知，如果其他参数给定且圆盘半径不变，三种边界条件下，相同厚度的圆盘弯曲振动的谐振频率是不同的，且比较研究可知，固定边界时的谐振频率大于自由边界条件时的谐振频率，但两种情况下自由边界条件和固定边界条件的谐振频率远大于简支边界条件的谐振频率。

图1、2分别是厚度为6 mm、直径为50 mm的厚圆盘在三种边界条件下的基频振型图和位移分布图。三种边界边界条件下，自由边界下中心位移最大，固定边界和简支边界下相比固定边中心位移相对大些，但边界处的横向位移为0，这些结论与板的振动理论是相符的。

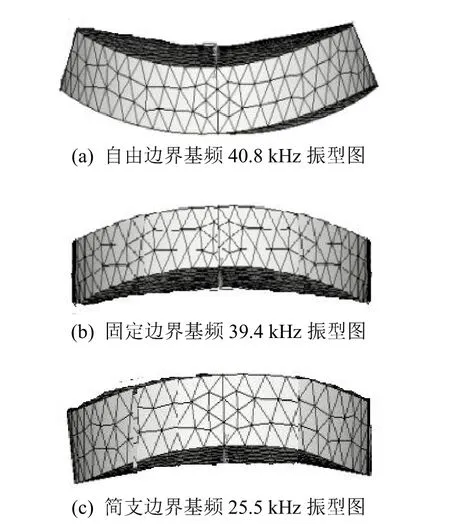
图1 不同边界下基频振型图Fig.1 Fundamental frequency mode diagrams under different boundary conditions

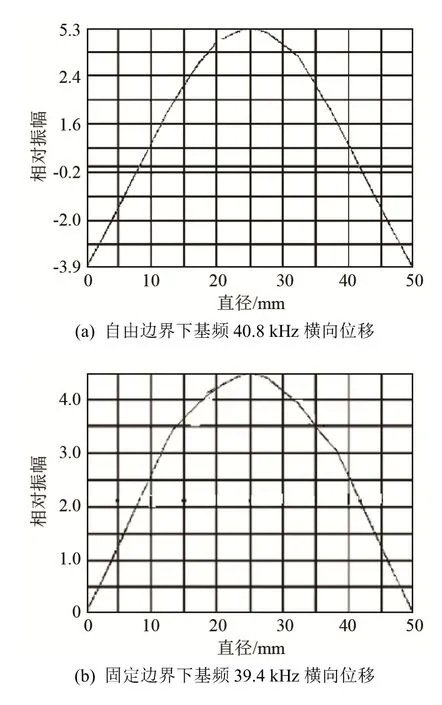
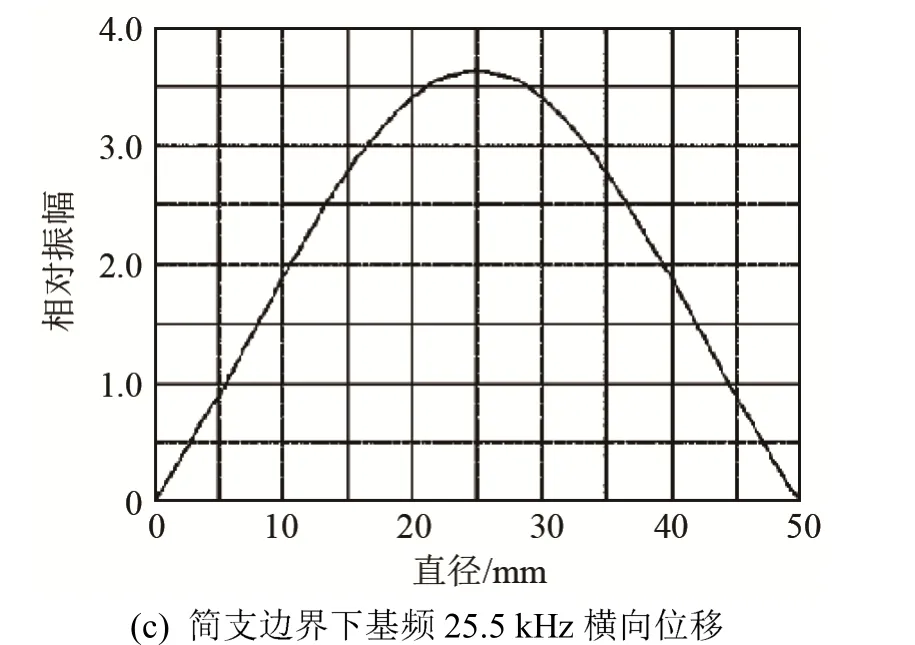
图2 不同边界下基频横向位移Fig.2 Transverse displacements of fundamental frequency under different boundary conditions

2 弯振厚圆盘的声场指向性推导

厚圆盘作轴对称的弯曲振动，由式(7)可得，其中心的横向位移和振动速度分别为

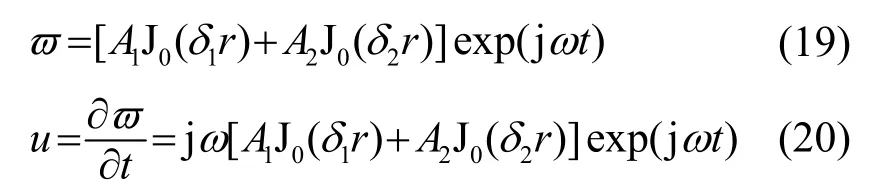
速度振幅为：U=jω[A1J0(δ1r)+A2J0(δ2r)]。取圆盘圆心O为坐标原点，其上表面位于xy平面，z轴垂直于盘面并过中心，如图1所示。厚圆盘所产生的辐射声场关于z轴是对称的，因此可认为场点p(r,θ)是位于xz平面上且到原点的距离为r，位移矢量r与z轴的夹角为θ。

图3 厚圆盘声场计算示意图Fig.3 Sound field calculation of thick disk

根据点状声源辐射声压的计算方法，可得厚圆盘弯曲振动所产生的辐射声压为

其中，l是圆盘表面的点源dS到坐标原点的距离，ρc0、k分别是特性阻抗和波数。r≫a，因此式(21)中l≈r，由图3有：l2=r2+ρ2-2rρcosβ，展开该式，且r≫ρ，所以l可表示为l=r-ρcosβ，式(15)变为

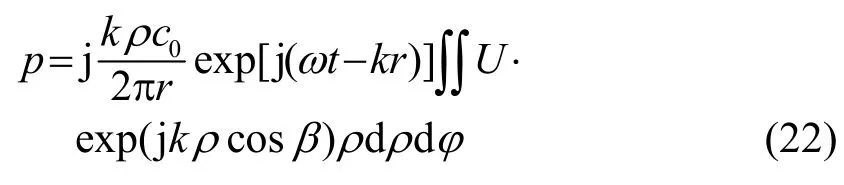
将以上结果代入式(16)，可得：

由以下贝塞尔函数的性质：

式(23)可写为

式(25)的推导过程并没有涉及厚圆盘的具体边界条件，因此其结果对各种边界条件下的辐射声场的计算都适用。由式(25)可得弯振厚圆盘辐射声场的指向性公式：

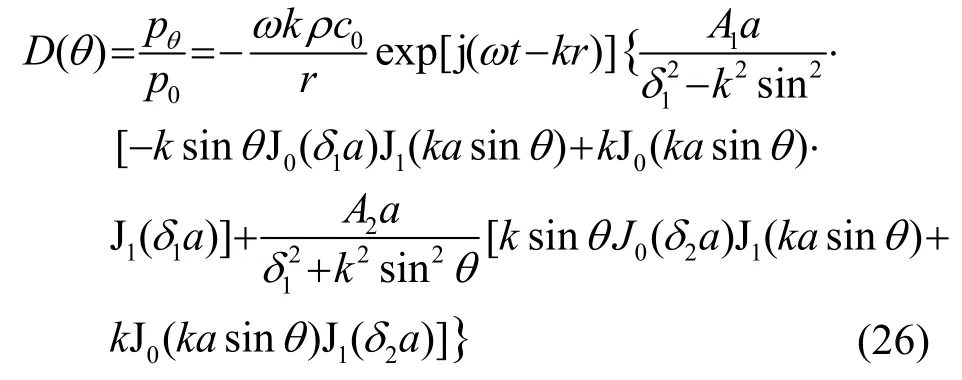
其中，A1、A2是由厚圆盘的边界条件来确定的常数。在不同边界条件下，厚圆盘的共振频率方程是不同的，因此其辐射声场指向性也是不同的，为了全面了解辐射声场特性，因此有必要进行以下研究。

3 弯振厚圆盘声场指向性的比较

取厚圆盘材料为45号钢，相关参数为：密度ρ=7.8×103kg·m-3，泊松比ν=0.28，弹性模量E=21.6×1010N·m-2，剪切模量G=8.4×1010N·m-2，波速c=5 050 m·s-1，频率可由方程(12)、(15)、(18)确定。由式(26)可知，当厚圆盘的尺寸和材料参数确定后，就可得到不同边界条件下弯曲振动厚圆盘的声场指向性。

3.1 不同边界条件下不同振动模式和相同尺寸厚圆盘的指向性比较

对厚度为16 mm、直径为50 mm的厚圆盘，通过式(26)对不同边界条件下的指向性进行研究，结果如图4～6所示。

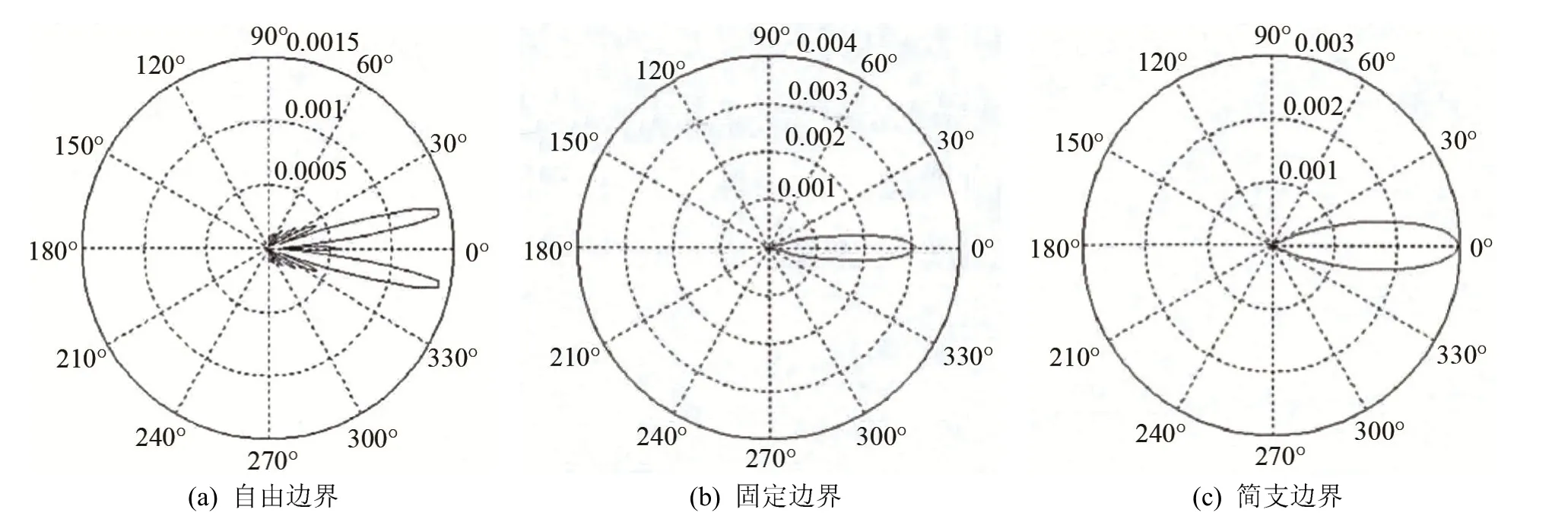
图4 振动模式基频n=1时的声场比较Fig.4 Comparison of the sound field at the fundamental frequency vibration mode of n=1

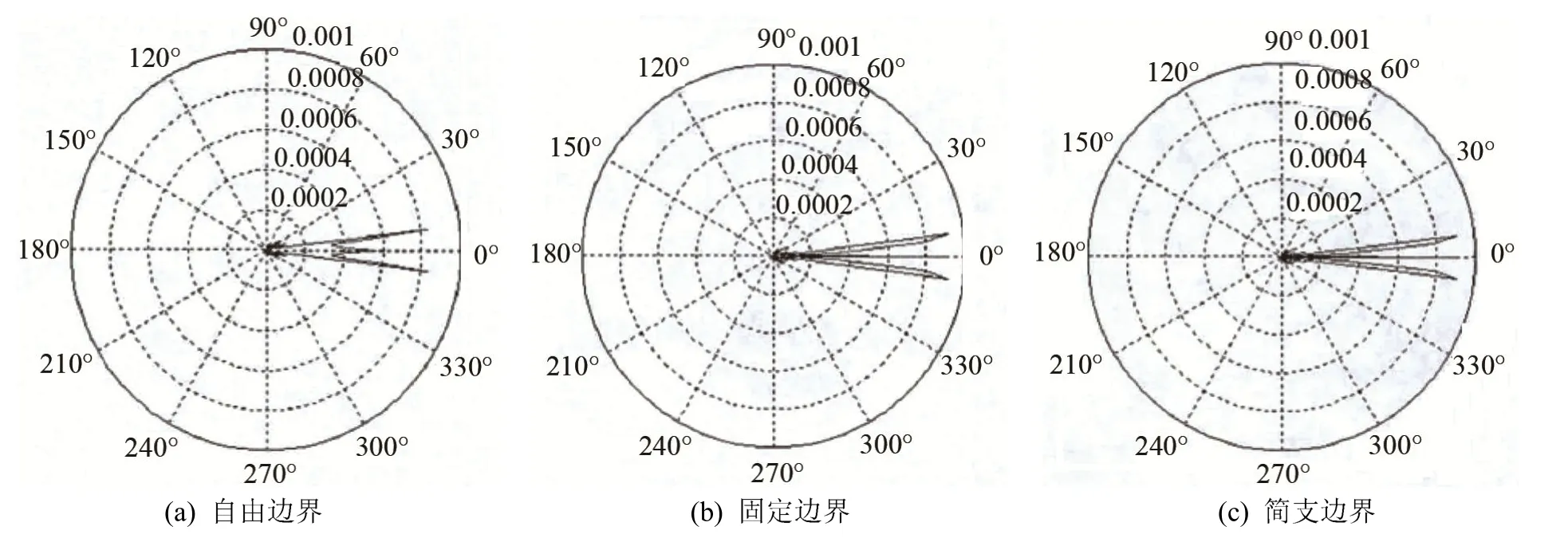
图6 振动模式n=3时的声场比较Fig.6 Comparison of the sound field at the fundamental frequency vibration mode of n=3

由图4～6比较可得自由、固定和简支边界弯曲振动厚圆盘辐射声场指向性各有特点。自由边界下弯振圆盘辐射能量在中心轴分布少，随着振动阶数的增加，厚盘辐射能量在中心轴上分布增多，相比之下，能量仍主要分布在两侧。简支、固定边界下弯曲振动圆盘辐射能量分布在中心轴上，能量分布相对较集中。随着振动阶数的增加，主瓣越来越尖锐，旁瓣逐渐增加，指向性变得越来越复杂。比较可得简支、固定边界下弯曲振动厚圆盘声场指向性相对较好，但固定边界下的弯曲振动厚圆盘的指向性更尖锐，自由边界下辐射声场指向性最不尖锐。随着振动阶数的增加，简支、固定边界下的弯曲振动厚圆盘的声场指向性变得比较尖锐，但旁瓣能量分布也较多，因此在实际应用时应统筹兼顾。在高频、大功率条件下，可应用厚盘能够克服薄盘机械强度不足的缺点，研究结果为大功率弯曲振动辐射体的应用提供参考。

3.2 不同边界条件下不同尺寸厚圆盘基频指向性的对比

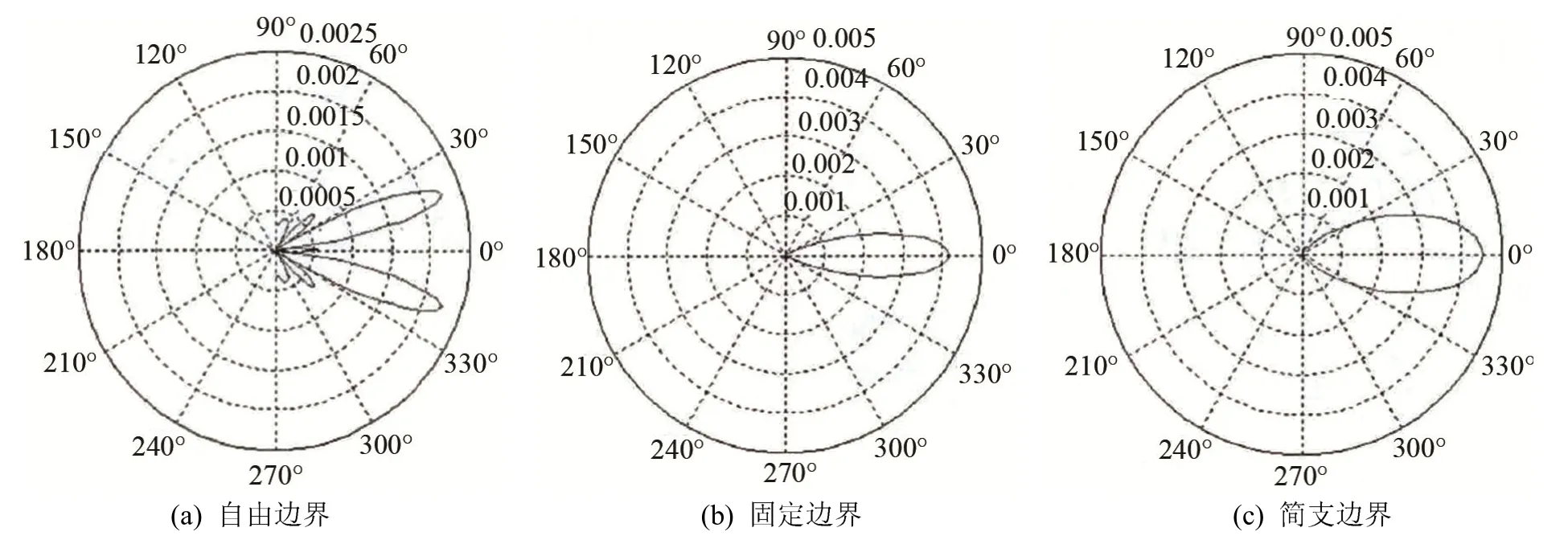
图7 振动模式n=1时的声场比较 (8 mm)Fig.7 Comparison of the sound field at the fundamental frequency vibration mode of n=1 (8 mm)

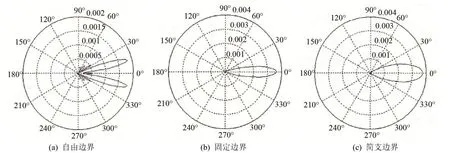
图8 振动模式n=1时的声场比较 (12 mm)Fig.8 Comparison of the sound field at the fundamental frequency vibration mode of n=1 (12 mm)

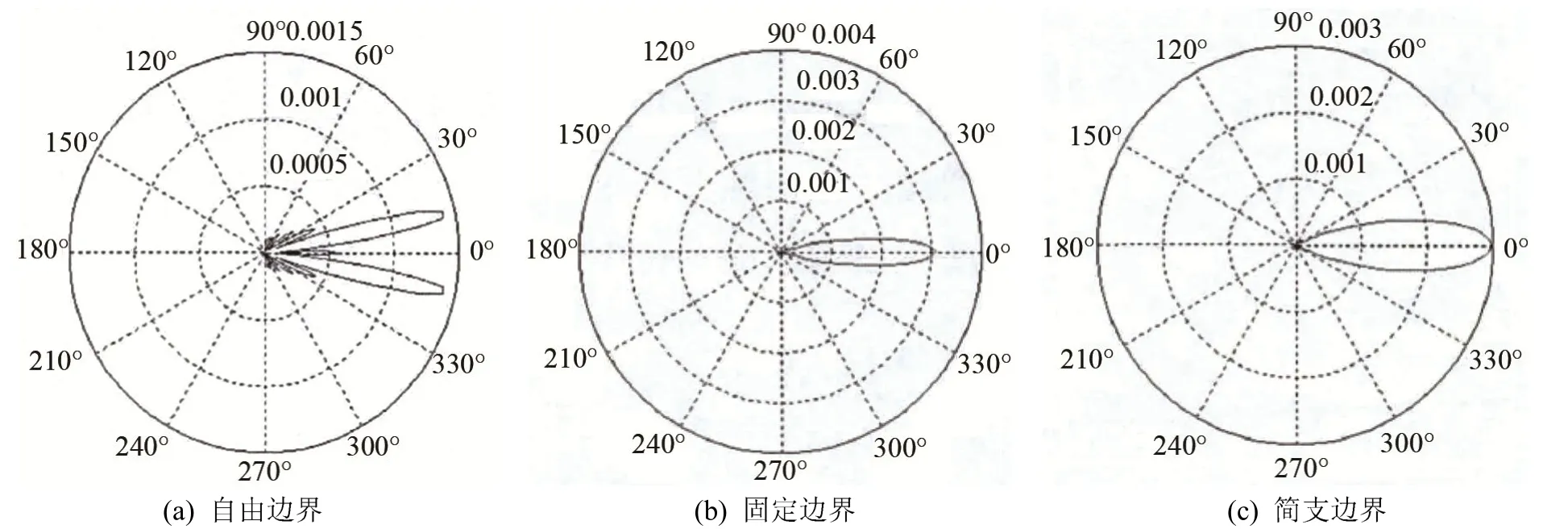
图9 振动模式n=1时的声场比较 (16 mm)Fig.9 Comparison of the sound field at the fundamental frequency vibration mode of n=1 (16 mm)

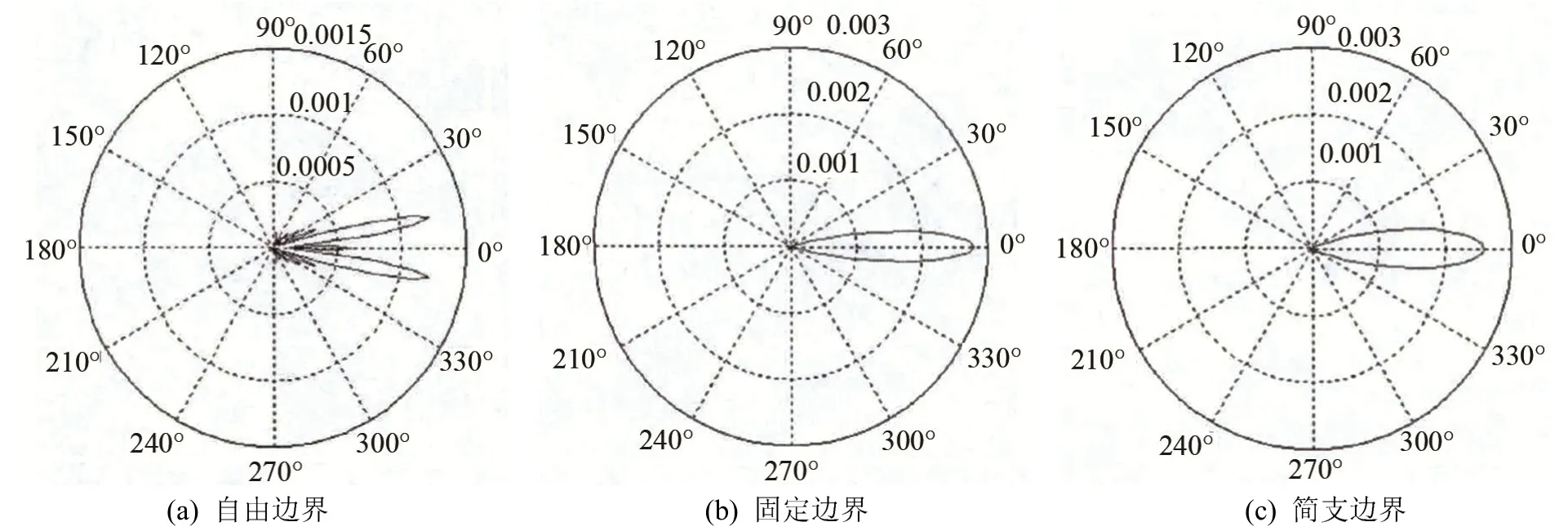
图10 振动模式n=1时声场比较 (20 mm)Fig.10 Comparison of the sound field at the fundamental frequency vibration mode of n=1 (20 mm)

取厚度分别为8、12、16、20 mm，直径为50 mm的圆盘，通过式(26)对不同边界条件下的基频指向性进行研究，结果如图7～10所示。

由图7～10可知，自由边界条件下基频振动模式的弯振厚圆盘在中心轴上能量分布较少，主要分布在中心轴两侧，辐射能量较分散，辐射主声束角宽度比较宽。固定边界和简支边界一阶振动模式下，弯振厚圆盘辐射能量分布在中心轴上，在中心轴两侧没有能量分布，都没有旁瓣，辐射主声束角宽度比较窄。对以上各图进行比较可知，在三种边界条件下，随着厚度的增加，指向性都变得越来越尖锐。其结果表明弯曲振动厚圆盘辐射能量在中心轴上变得越来越集中，声场指向性好。在同边界条件基频振动模式下，厚板指向性比薄板尖锐。

3.3 指向性与材料的关系

图11 不同材料圆盘的70 kHz声场Fig.11 Sound fields of disk with different materials at 70 kHz

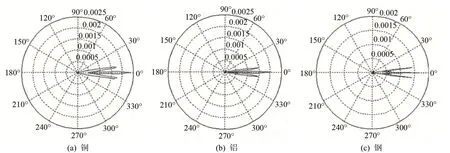
图12 同尺寸不同材料圆盘声场Fig.12 Sound fields of the same size disk with different materials

在同一弯曲振动谐振频率下(取频率为70 kHz)，材料分别为铝、钢、铜的厚盘指向性如图11所示。从图11可看出，对固定边界条件下，同一种谐振频率、不同材料的指向性变化不大，这说明厚盘材料对其指向性的影响较小。图12为同尺寸、不同材料厚盘的声场指向性图。由图12可知，对于同尺寸、不同频率的厚盘，钢材料的指向性最好，铜材料最小，铝材料次之，因为同尺寸下钢材料厚板的谐振频率最大，而铜材料对应的频率最小。

4 结 论

(1)厚盘辐射体机械强度高，横向尺寸小，在高频大功率声辐射条件下经常被应用。应用Mindin理论结合具体边界条件计算得到了3种边界条件下厚圆盘弯曲振动的谐振频率方程，并给出了3种边界条件下圆盘基频的振型图和横向位移分布图。

(2)推导出3种不同边界条件下厚圆盘辐射声场指向性的数值表达式，利用计算机编程对其声辐射特性进行研究。在不同边界条件下，尺寸相同的厚圆盘各阶指向性的尖锐程度是不同的，研究结果表明固定边界条件下的辐射声场指向性最尖锐，自由边界条件下声场指向性最尖锐，简支边界条件次之。

(4)对不同尺寸、不同边界条件厚圆盘指向性的对比可知，基频振动模式下，随着厚度的增加，各边界条件下厚圆盘的辐射声场指向性变得越来越尖锐。研究结果对厚盘弯曲振动辐射体的实际应用可提供理论依据。

(5)对于谐振频率和边界条件相同而材料不同的圆盘的指向性，材料对其声场指向性的影响较小；对于同尺寸、不同频率的厚圆盘，材料对厚盘声场指向性的影响较大。