近红外光谱定性定量检测牛肉汉堡饼中猪肉掺假

白 京，李家鹏*，邹 昊，田寒友，刘 飞，李文采，王 辉，张振琪，王守伟*

（中国肉类食品综合研究中心，北京食品科学研究院，肉类加工技术北京市重点实验室，北京 100068）

在肉制品加工过程中，肉制品的颜色、形态被破坏，肉眼难以直观判断是否掺假，因此掺假肉经常出现在一些加工制品中，如肉丸、肉馅、汉堡肉饼等[1]。随着我国居民生活水平的提高，汉堡以其方便食用、口感口味兼具的特点占据较高的市场份额。很多制造厂商受利益驱使，使用猪肉、鸭肉等低价位品种肉以及动物内脏等进行掺假，严重损害广大消费者的利益。目前对肉品掺假的检测方法，集中在蛋白质酶联免疫吸附法、核酸聚合酶链式反应等[2-4]，这些检测方法耗时耗力或对样品有损伤，不能满足快速检测的需求。

近红外光谱技术作为一种无损、快速、操作简单的检测技术，在肉品品质测定、品种鉴别和产品溯源等方面有很多应用[5-9]，而在肉品掺假检测方面主要集中在瘦肉品种鉴别等[10-16]。有学者在应用近红外光谱技术检测牛肉汉堡饼中的掺假方面进行研究，如Zhao Ming等[17]利用近红外光谱技术对新鲜、解冻、冷冻3 种状态下的内脏掺假牛肉汉堡饼进行定性定量检测，其中应用偏最小二乘判别分析（partial least squares discrimination analysis，PLS-DA）模型定性判别正确率分别为95.5%、91.3%和88.9%，应用PLS定量检测新鲜和解冻状态下内脏掺假牛肉汉堡饼模型的R2分别为0.96和0.86，可以看出解冻状态样品检测的准确率较低。Morsy等[18]将新鲜状态的猪肉、内脏、脂肪分别按照不同比例与牛肉混合，应用偏最小二乘回归（partial least squares regression，PLSR）方法定量检测掺假模型的R2分别为0.96、0.94和0.95，均能较好预测掺假，未见对不同掺杂比例的猪肉和脂肪进行检测预测。由此，应用近红外光谱技术检测牛肉汉堡饼掺假的研究取得了一定的成果，但还存在一些空白。一是肉的品种对近红外光谱影响较大[19]，不同肥肉占比的肉饼掺假检测研究主要集中在国外，有必要对国内牛肉中掺假检测方法进行研究；二是新鲜状态与解冻状态检测结果不尽相同，考虑到牛肉汉堡肉饼主要在解冻状态下进行加工储藏，因此也有必要进行不同肥肉占比的牛肉中猪肉掺假解冻状态下的研究。

牛肉汉堡饼根据肥肉含量和添加其他辅料的不同分为高品质和低品质两种，高品质牛肉汉堡饼中仅含有肥肉和牛瘦肉，且瘦肉比例在75%～100%之间[20]。本实验研究选取高品质解冻状态下的牛肉汉堡饼为掺假对象，以相对较低价位的猪肉进行掺假，采集样品的近红外光谱信息，选取合适的预处理方法并分别建立定性和定量模型，提出一种快速检测不同肥肉占比的解冻牛肉汉堡饼中猪肉掺假的定性定量分析方法，为国内牛肉汉堡饼的掺假快速检测提供技术支撑。

1 材料与方法

1.1 材料

猪腿肉（品种为杜长大） 北京永辉商业有限公司；牛瘦肉取自牛霖、牛肥肉（鲁西黄牛） 北京穆森伟业清真食品有限责任公司；以上肉样品均为冷鲜肉，样品1 h内运至实验室后密封保存于0～4 ℃冷库中。

样品组成：实验样品分为未掺假和掺假牛肉汉堡饼两类，其中未掺假样品中瘦肉比例为75%～100%之间，依次递减2.5%，共11 个配比，每个配比3 个平行，共33 个样品；掺假样品中瘦肉比例为75%～100%（牛瘦肉及掺加的猪瘦肉比例之和）之间，肥肉比例为0%～25%，猪瘦肉占总量比例为0%～40%，为在保证代表全部样品的前提下简化实验样品数量，通过MyDesign软件混料设计得到14 个配比，每个配比3 个平行，共42 个样品，如表1所示。

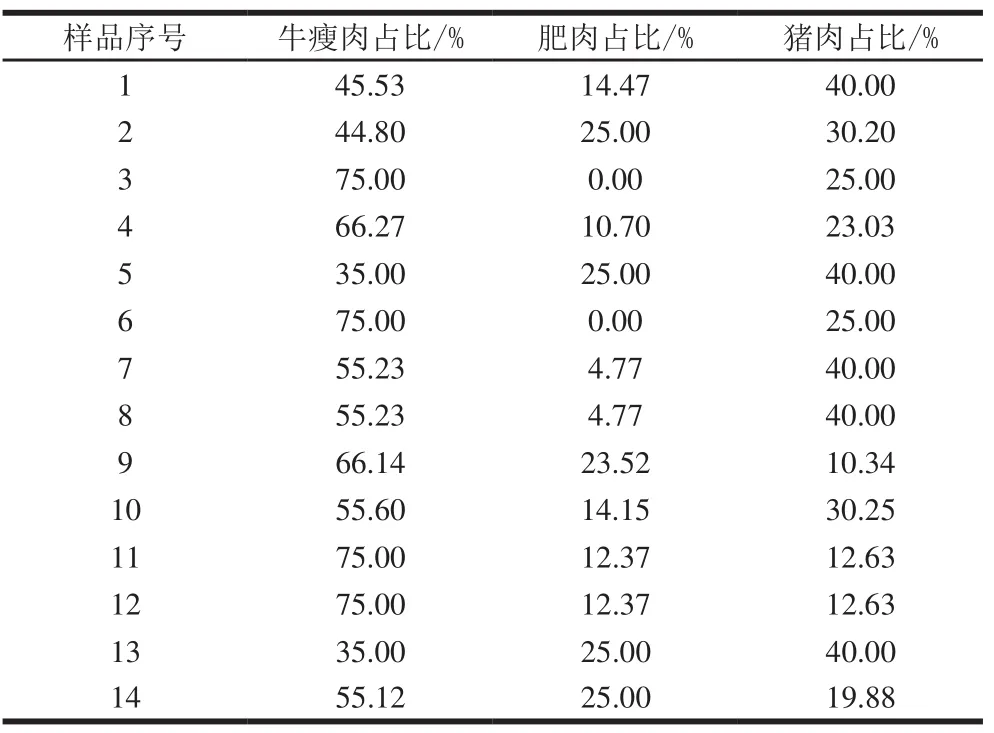
表 1 掺假样品配比Table 1 Proportions of adulterated samples

样品制备：为保证模型准确，将原料肉的表皮、筋膜、肥肉、血块等剔除，按照比例混合掺杂。将掺杂好的样品分别放置在-18 ℃冷冻库中保存。实验开始前，将样品取出放置在0～4 ℃冷库中24 h解冻。对解冻完的样品使用绞肉机，以直径为3 mm的板孔绞成小颗粒肉糜，绞2 次，保证样品掺杂均匀。每个样本称取180 g，使用直径为8 cm的汉堡模具压实压平，之后采集近红外光谱。

所有实验在1 个月内完成，保证肉品冷冻期间化学成分基本无变化[21]。

1.2 仪器与设备

MPA近红外傅里叶变换光谱仪 德国布鲁克公司；电子天平 艾德姆衡器（武汉）有限公司；绞肉机合肥荣电实业股份有限公司。

1.3 方法

1.3.1 光谱采集

为保证准确采集到样品表面的光谱数据，利用该近红外光谱仪的旋转器采集，光谱采集软件为OPUS7.0。将样品放置在样品杯中压实，光谱仪扫描范围为3 600～12 500 cm-1，扫描次数为64 次，分辨率为32 cm-1。实验时环境温度为（25±1）℃，相对湿度为（60±5）%，每个样品采集3 次光谱数据，取其平均值作为该样品的光谱数据。

1.3.2 样品集划分

为保证模型的预测精度，将75 个样本按顺序以3∶1分为校正集和验证集，样品数分别为57 个和18 个，样品集划分结果如表2所示，校正集和验证集中掺假样品和未掺假样品的分布较为一致。

表 2 样本集划分结果Table 2 Composition of sample sets

1.3.3 数据处理方法

定性判别方法选取非线性判别和线性判别两类方法中应用较为广泛的SVM和PLS-DA。SVM算法是一种基于有限样本统计学习理论的有监督机器学习方法，通过非线性映射将输入变量映射到一个高维的特征向量空间，在高维特征空间进行线性回归，依据结构风险小化原则，在高维空间构造优分类超平面，较好解决小样本、非线性等问题[22-23]。PLS-DA算法是基于判别分析的PLS算法，应用类别变量代替浓度变量，同时从光谱阵和浓度阵中提取载荷和得分，消除光谱间可能存在的复共线关系[24]。定性判别时将未掺假样品组的类别变量设为0，掺假样品组的类别变量设为1。

选取应用较为广泛的PLSR方法，以猪肉掺假的比例值为理化指标，建立不同肥肉占比的解冻牛肉汉堡饼中猪肉掺假比例的定量检测模型，其中未掺假样品的猪肉掺假比例为0。

1.3.4 评价指标

通过比较样品判别正确率确定最优定性判别方法，定量检测时比较校正集的相关系数（Rc）与预测集的相关系数（Rp）、校正均方根误差（root mean square error calibration，RMSEC）和预测均方根误差（root mean square error prediction，RMSEP）评价模型[25]。

数据处理以及画图采用Matlab 2017a、Excel 2017软件编程实现。

2 结果与分析

2.1 原始光谱测定结果

图 1 样品原始光谱图像Fig. 1 Original NIR spectra of samples

图1为所有样品的原始光谱图像，比较图1a、b可知，未掺假样品和掺假样品的光谱曲线趋势相近，但掺假样品相对未掺假样品变化幅度更大，未掺假样品的光谱曲线比掺假样品更加平滑，尤其在7 000～4 000 cm-1之间比较明显。在近红外中峰宽代表信号的强弱[26]，掺加猪肉会引起光谱信号变弱。图1c中3 条曲线分别为肥肉占比25%下猪肉掺假比例40%、19.88%和未掺假的样品光谱曲线，可以看出在整个光谱范围内并未有随猪肉掺假比例降低光谱吸收度下降或升高的规律，说明需要通过化学计量学方法提取光谱中的有效信息[26]。

2.2 主成分分析-支持向量机（principal component analysis-support vector machine，PCA-SVM）模型判别

2.2.1 PCA结果

由于原始光谱数据维数较高，若直接利用原始数据建模会影响计算速度且模型运算时间会过长。PCA是一种较为常见的数据降维处理方法，可以利用尽可能少的主成分代表原始光谱数据。图2为前3 个主成分的两两得分图（PC1和PC2，PC2和PC3），3 个主成分对描述解冻牛肉汉堡饼样品差异的贡献率分别为71.74%、26.48%、0.97%。从得分图可以看出，掺假样品和未掺假样品之间不能明显区分，但是两类的重心可以区分。PC2对两组样本的部分分离做出了较为显著的贡献，而PC3则描述了每组样本中的变化，其中掺假样本组中变化受影响较高。使用前3 个主成分的累计贡献率已经达到99.19%，能够准确反映样品光谱信息。

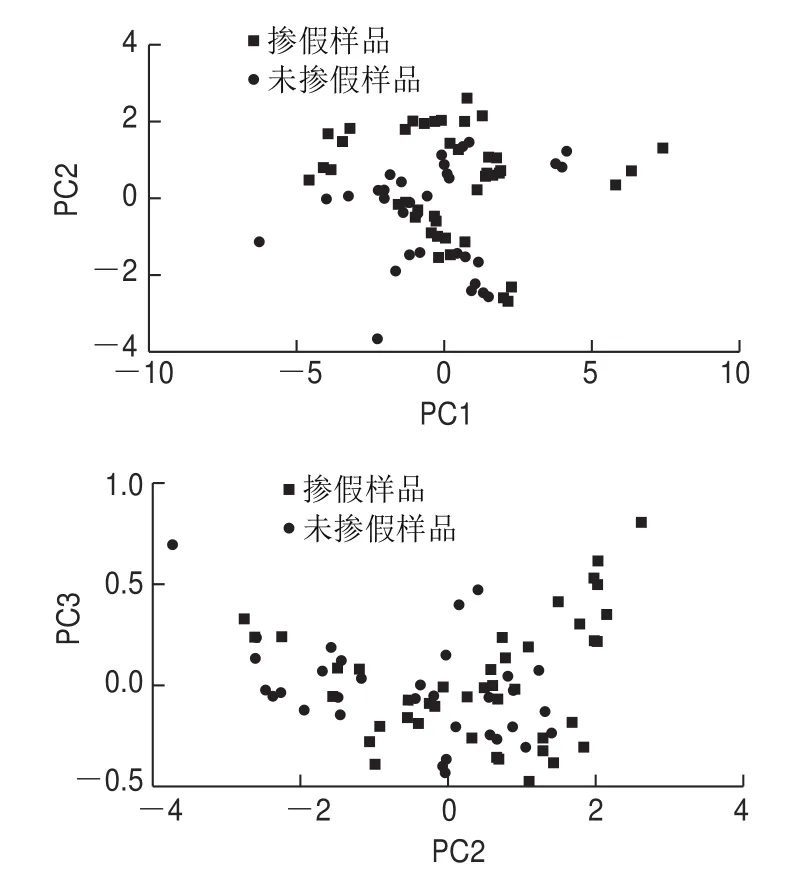
图 2 前3 个主成分得分图Fig. 2 Scores plots of first three principal components

2.2.2 模型的建立

由图2可知，两组样品的判别区分不能直接实现，而SVM判别非线性可分数据是通过选取合适的核函数，解决低维空间映射到高维空间增加计算复杂度的问题，得到高维空间函数进行非线性可分数据的分类。常用的核函数主要有多项式核函数、径向基核函数（radial basis function，RBF）、线性核函数、Sigmoid核函数等，其中RBF核函数超参数数量小、数值难度低、逼近速度快且应用最为广泛。本实验选取RBF作为模型的核函数，惩罚因子C和核参数γ是RBF核函数中需要确定优化的两个重要参数[27]。本实验通过比较不同折数交叉验证、粒子群算法（particle swarm optimization，PSO）和遗传算法（genetic algorithm，GA）等算法确定最优的两参数，以提高模型的预测精度，选择的参数以及最终判别正确率如表3所示。

由表3可以看出，通过交叉验证方法选取核参数的SVM模型判别正确率相对较高，其中当交叉验证折数为10，惩罚因子C为64，核参数γ为0.09时，校正集判别正确率最高为100%，验证集判别正确率最高为83%。验证集中被误判的样品各不相同，分别为表1中10号掺假样品（猪肉占比30.25%、脂肪占比14.15%）、11号掺假样品（猪肉占比12.63%、肥肉占比12.37%）、15%肥肉占比的未掺假样品。

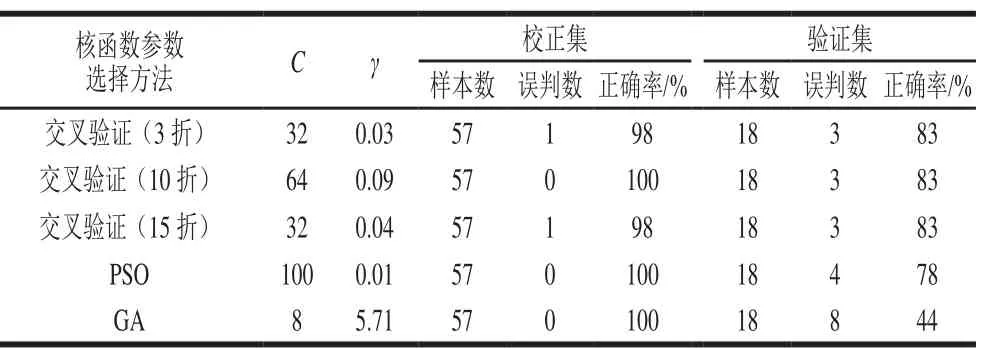
表 3 不同方法选择的核函数参数的SVM模型判别结果Tabel 3 Classification results of SVM model with kernel function parameters selected by different methods

2.3 PLS-DA模型判别

选取合适的主因子数可以保证PLS-DA模型有较高的预测准确度和准确性，主因子数选择是建立PLS-DA模型的第1步。本实验采用百叶窗法交叉验证确定模型的最佳主因子数。选择的主因子数初始范围为1～20，步长为1，分别建立PLS-DA模型，得到不同的交叉验证均方根误差（root mean square error of cross-validation，RMSECV）。主因子数选取按照尽可能少的主因子数且RMSECV尽可能低的原则，当主因子数为13时，为最优条件。

对校正集原始光谱数据做标准正态变换（standard normal variate，SNV）预处理后，选取主因子数为13，建立PLS-DA判别模型，判别时以0.5为阈值，高于0.5的判别为掺假样品，低于0.5的判别为未掺假样品，判别结果如图3a所示，掺假样品和未掺假样品的判别正确率均为100%。为进一步验证所建立PLS-DA模型，将验证集样品的SNV预处理后的光谱数据代入上述PLS-DA校正模型并计算判别正确率，结果如图3b所示，掺假样品和未掺假样品的判别正确率也均为100%。结果表明，应用PLSDA方法判别不同肥肉占比的牛肉汉堡饼中的猪肉掺假可行，且预测精度较高。由上述2 种判别结果可知，PLS-DA作为一种监督模式识别方法，构造因素时考虑到了辅助矩阵以代码形式提供的类成员信息[28]，相对SVM这种无监督模式判别方法，更加适合肉类掺假鉴别，具有更加高效的鉴别能力，而这一结果也与Zhao Ming等[17]的研究相一致。

图 3 PLS-DA模型判别结果Fig. 3 Classification results of PLS-DA model

2.4 PLS定量检测模型

表 4 不同预处理方法的PLSR模型Table 4 PLSR models with different pretreatment methods

图 4 PLSR模型预测结果Fig. 4 Prediction results of PLSR model

分别采用均值中心化（mean centering，MC）（数据增强类算法）、Savitzky-Golay结合一阶求导（savitzkygolay derivative，SG-1st）（导数类算法）、Savitzky-Golay平滑（savitzky-golay smoothing，SGS）（平滑类算法）、SNV和多元散射校正（multiplication scatter correction，MSC）（信号校正类算法）等几种具有代表性的预处理方法[25]，对原始光谱数据预处理后应用PLSR方法建模，建模结果如表4所示。应用MC预处理后，预测系数较高，且RMSEC与RMSEP的值均较低且二者相差较小，该模型比较准确，其预测值与真实值的关系如图4所示。由图4b得知，当掺假比例在20%以上时，预测值均匀分布在预测线两侧，真实值与预测值相差较小，而掺假比例低于20%时，真实值与预测值相差较大，说明该模型的检测限为20%，后期可选取合适样品数量或优化模型参数方法进一步降低检测限[29]。

3 结 论

本研究基于近红外光谱技术，对不同肥肉占比的牛肉汉堡饼中的猪肉掺假进行定性判别和定量检测研究，得出了以下结论：1）应用SVM和PLS-DA算法均可实现不同肥肉占比的牛肉汉堡饼中猪肉掺假的定性鉴别，其中PLS-DA模型判别效果更好，验证集和校正集判别正确率均为100%。2）应用PLSR算法可以实现不同肥肉占比的牛肉汉堡中猪肉掺假比例的定量检测，校正集和验证集的相关系数分别为0.968 9和0.861 1，RMSEP为7.221%。

本实验中选取的牛肉汉堡饼为高品质汉堡饼，未考虑其他辅料的影响，后期可选取低品质牛肉汉堡饼为研究对象，丰富配方内容，进一步扩大该方法的应用范围。另可进一步优化参数或选择合适样品数量进一步降低该方法检测限。