基于FOA-SVR模型的矿井底板突水量预测应用研究

刘梦杰，朱希安，王占刚

(北京信息科技大学，北京 100101)

矿井突水即“影响、威胁矿井安全生产，使矿井局部或全部被淹没并造成人员伤亡和经济损失的矿井涌水事故”，与瓦斯、煤尘并列为矿山生产建设过程中的三大主要灾害。当矿井涌水量超过正常的排水能力时，就会发生矿井水灾事故。突水事故的发生，会严重影响煤矿行业的安全生产，因此有效的突水预测和实时的突水预报是降低煤矿水害事故多发的重要途径之一[1]。

目前对煤层底板突水预测分析大多局限于定性研究，最终得到煤层底板突水量的等级划分，而对实际突水量预测的定性研究却很少[2]。刘北战等[3]通过PCA-SVR方法用较低维数包含了影响底板突水的多个因素，保证了预测效率及精度，得到了样本点的突水等级；高卫东等[4]通过粒子群算法优化支持向量机方法针对底板突水量进行预测，并验证了预测结果与实际情况吻合度较高，但也仅得到了样本点的突水等级。之后，秦洁璇等[1]将SVR模型用于矿井底板突水量的预测，但SVR模型在单独进行突水量预测时，存在训练过程模型参数选取盲目性的问题。因此，本文通过FOA-SVR模型来实现矿井底板突水量的预测，有效地避免了上述问题。

1 FOA-SVR底板突水量预测模型整体设计

当发生矿井水灾时，按照突水点位置的不同，可以分为顶板突水、底板突水和侧向突水三种类型，不同类型诱发突水的原因是不一样的。由于底板突水的发生频率相对更高，因此本文设计了一种FOA-SVR底板突水量预测模型，可以为该类型突水的突水量计算提供参考，如图1所示。

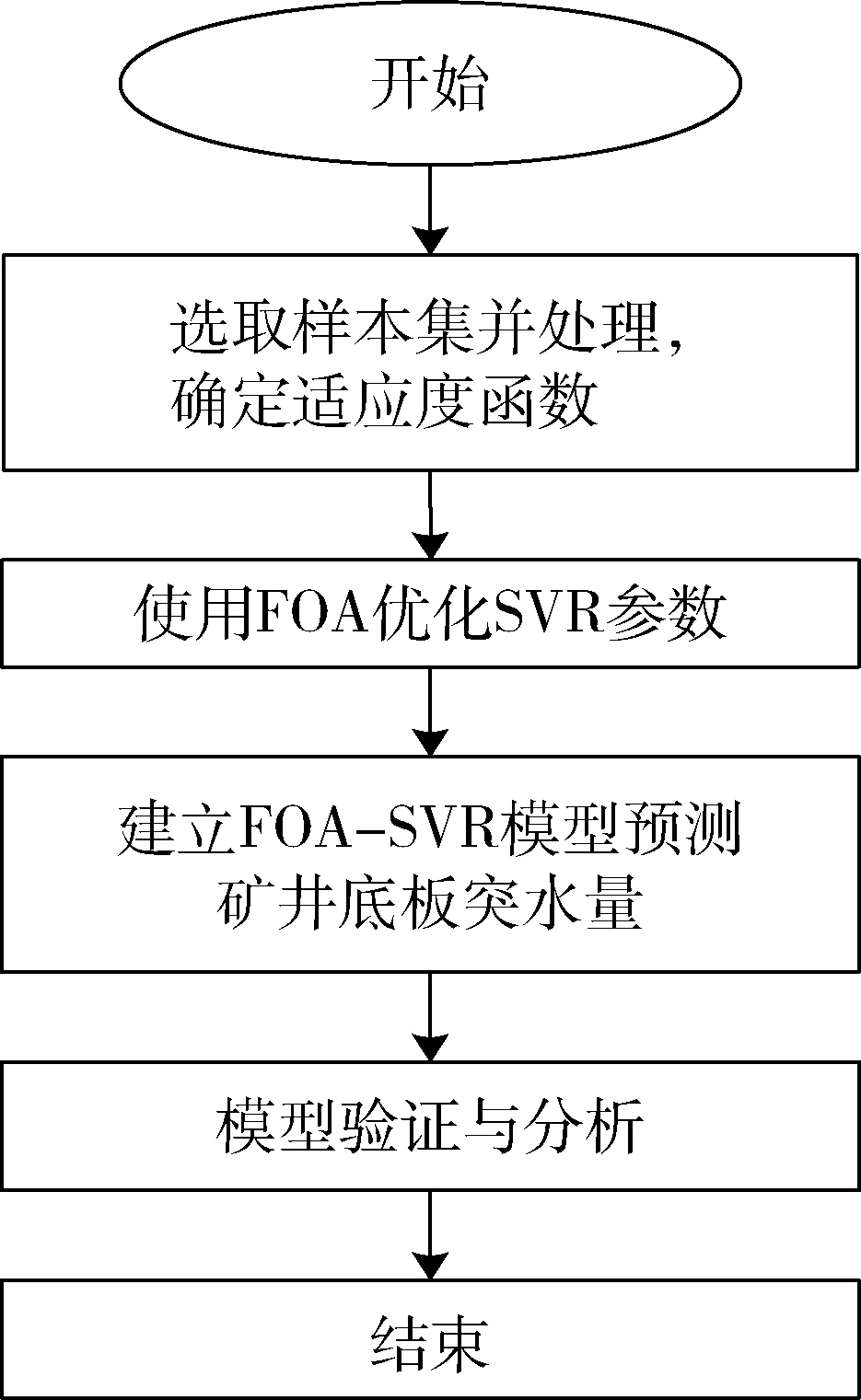
图1 FOA-SVR底板突水量预测模型Fig.1 FOA-SVR prediction model forfloor water inrush quantity

本模型首先需要整理国内一些典型的底板突水样本集并进行归一化处理消除量纲以及单位的影响，并将样本集分为训练集和测试集两个部分。初始化果蝇种群参数之后调用SVR算法计算适应度值，并迭代寻优得到优化之后的SVR模型参数，通过训练集学习建立FOA-SVR底板突水量预测模型，然后对测试集中的样本进行预测，最后对该模型进行了实验分析与验证。

1.1 FOA-SVR模型

20世纪90年代中期，VPANIK等提出了支持向量机模型，该模型可以较好地解决下凹样本、非线性、过学习和局部极小点等问题[5]。但是使用该模型时需考虑参数的选择问题，这一直都是解决实际问题时所遇到的一大难点，它们的选取会直接影响模型的复杂程度以及预测精度[6]。

果蝇算法是继遗传算法、粒子群算法、蚁群算法等典型的优化算法之后，Wen-Tsao PAN于2011年从果蝇的觅食行为中得到启发而提出的一种新型群体智能优化方法。与其他的优化算法相比较，果蝇算法实现起来比较简单，它只有两个参数需要调节，并且全局寻优能力强，对实际应用具有一定的帮助[7]。

FOA-SVR模型即通过果蝇算法优化支持向量回归机参数，可以有效地解决参数选择问题。

1.2 适应度函数

适应度函数也称为评价函数，可以将优化问题的目标函数与果蝇个体的适应度值之间建立某种映射关系，即在果蝇寻优过程中通过适应度函数实现对优化问题目标函数的寻优。在FOA-SVR模型中适应度函数是建立该模型的关键。

适应度函数的选择会影响FOA的收敛速度以及能否找到最优解，同时适应度函数的建立应该尽可能的简单，使计算的时间复杂度最小。对实际问题进行分析可知，yi,test(x)为该模型所预测的某突水点的突水量，见式(1)。

(1)

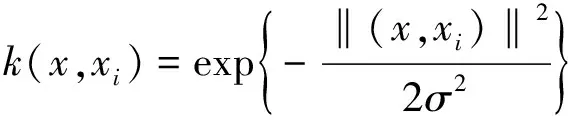
(2)

式中,σ为核函数的宽度。

本文所选用的适应度函数计算见式(3)。

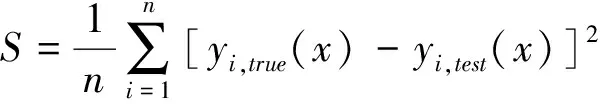
(3)

式中：n为测试样本总个数；yi,true(x)为某突水点的实际突水量。

代入求解得适应度函数表达式见式(4)。

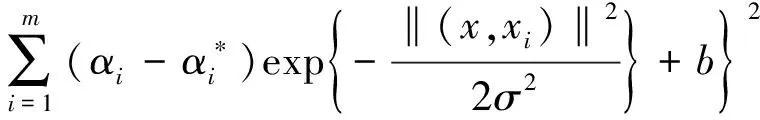
(4)

通过计算预测突水量与实际突水量之间的均方误差，使得该取值最小，即预测精度最高。

2 FOA-SVR模型算法原理

2.1 FOA模型算法原理

FOA模型算法通过模拟果蝇个体以及群体的觅食过程，经过适当的迭代过程可以得到全局最优解[6]。

果蝇迭代搜寻食物的步骤如下所示。

步骤1：首先初始化果蝇群体位置(Xaxit,Yaxit)，设置果蝇群体规模n及迭代次数m，见式(5)。

(5)

式中,Rand(LR)为果蝇群体的随机位置。

步骤2：利用嗅觉搜寻食物的飞行距离及方向确定果蝇个体的位置，见式(6)。

(6)

式中,Rand(FR)为果蝇个体的固定步长。

步骤3：由于食物的位置是未知的，先估计果蝇距离原点坐标的距离Di(式(7))，距离越远，嗅到的味道浓度越低，因此味道浓度判定值Si取距离的倒数(式(8))[7]。

(7)

Si=1/Di

(8)

步骤4：将味道浓度判定值代入到味道浓度判定函数(fitness function)即适应度函数中，求出该果蝇个体的味道浓度(式(9))。

Smelli=F(Si)

(9)

步骤5：根据味道浓度判定函数在果蝇群体中找出味道浓度最大的果蝇个体(式(10))。

[bestsmellbestindex]=max(smell)

(10)

式中：bestsmell为味道浓度最大的果蝇个体所对应味道浓度；bestindex为该果蝇个体对应的坐标位置。

步骤6：保留最佳味道浓度值及该果蝇对应的(X,Y)坐标位置，此时果蝇通过其敏锐的视觉朝着这个位置飞去，计算见式(11)和式(12)[8]。

smellbest=bestsmell

(11)

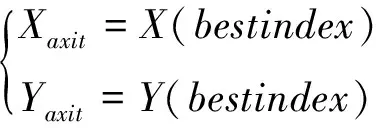
(12)

步骤7：进入迭代寻优过程，重复步骤2至步骤5，并判断味道浓度是否优于上次，如果是，则继续执行步骤6。

2.2 SVR模型算法原理

支持向量机回归模型的目的是通过学习训练集中的样本点，使得它们可以尽量的拟合到线性模型yi=ω·φ(xi)+b上。为了使支持向量回归机保持较好的稀疏性[2]，定义不敏感损失函数ε>0，假设所有的训练数据在精度ε下使用线性函数进行拟合，令z=yi-ω·φ(xi)-b,则加入松弛因子ξ,ξ*之后，SVR问题转化为求优化目标函数最小化问题(式(13))[5]。

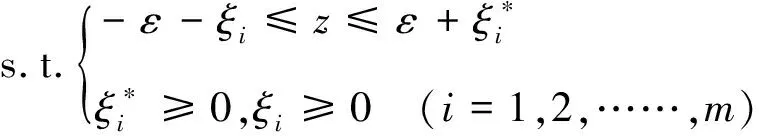
(13)

式中,C为惩罚因子。

求得SVR问题的对偶形式，计算见式(14)。

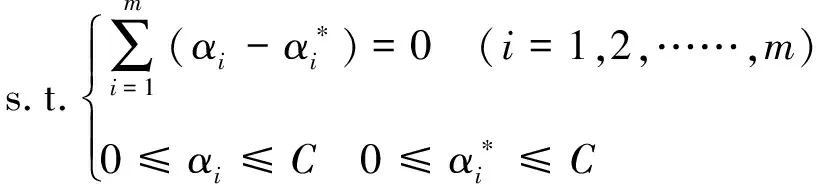
(14)

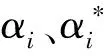
通过求解，求得支持向量回归机的决策函数，见式(15)。

(15)

式中：m为支持向量回归机个数;核函数是k(xi,xj)=φ(xi)φ(xj)。

2.3 FOA-SVR模型算法原理

选择不同的核函数可以构造出不同的SVR模型。本文选用径向基核函数，相比于其他的核函数，它只需要确定一个参数，并且函数复杂度较低。径向基核函数表达式见式(16)。

(16)

参数ε控制着回归函数对于样本数据不敏感区域的宽度；参数C反映了算法对超出ε的样本数据的惩罚程度；参数σ为核函数的宽度参数，控制了函数的径向作用范围[9]。为了选择出最优的SVR参数，我们通过FOA来解决这个问题，对参数(ε,C,σ)进行训练寻优，FOA寻优流程如图2所示。

图2 FOA寻优流程Fig.2 Optimization process of FOA

3 基于FOA-SVR模型的矿井底板突水量预测实例

3.1 突水因素选择

底板突水受到多种因素的综合影响。其中,水压是底板突水的基本动力，决定着是否会发生突水以及突水量的大小；含水层的富水性决定突水量的大小及稳定性；隔水层有助于抑制底板突水，当其他条件都一样时，隔水层厚度越大越不容易发生突水[10]；采动裂隙是由矿压和底板高承压水共同作用产生的结果，由它所形成的导水通道会诱发底板突水的产生，其扩展程度受到多种因素的共同影响；断层可缩短煤层与含水层之间的距离，逐渐形成突水通道，断层构造与矿压相互作用，使底板裂隙进一步扩展，隔水能力大大降低，更易发生突水现象[11]。

结合实际情况以及相关资料综合分析，选取水压、含水层厚度、隔水层厚度、底板采动裂隙带深度以及断层落差5个因素作为影响预测底板突水的主要因素，以此作为预测模型的输入参数，输出即为预测的突水量[3]。其中，输入参数特征值的选取原则为：可以完全定量的用定量数据表示，不能定量的用二分量表示。则文中含水层厚度采用二分量类型，1表示薄层灰岩，0表示厚层灰岩；其他属性则采用连续性参数进行设置[1]。

3.2 样本集建立

样本集的选取要具有代表性，且每一个样本应该包含相同的属性特征[1]。笔者收集整理了一些煤层底板突水案例并从中选出18个，其中14个作为训练样本集，4个作为预测样本集。由于样本集中多指标的量纲和数量级不相同，为消除不同量纲数据对评价结果的影响，需要对样本数据进行标准化处理[12]，选用Min-Max标准化转换方法，转换公式为式(17)。

x′=(x-xmin)/(xmax-xmin)

(17)

式中：xmax为样本数据的最大值；xmin为样本数据的最小值。

经过处理之后标准化样本集见表1。

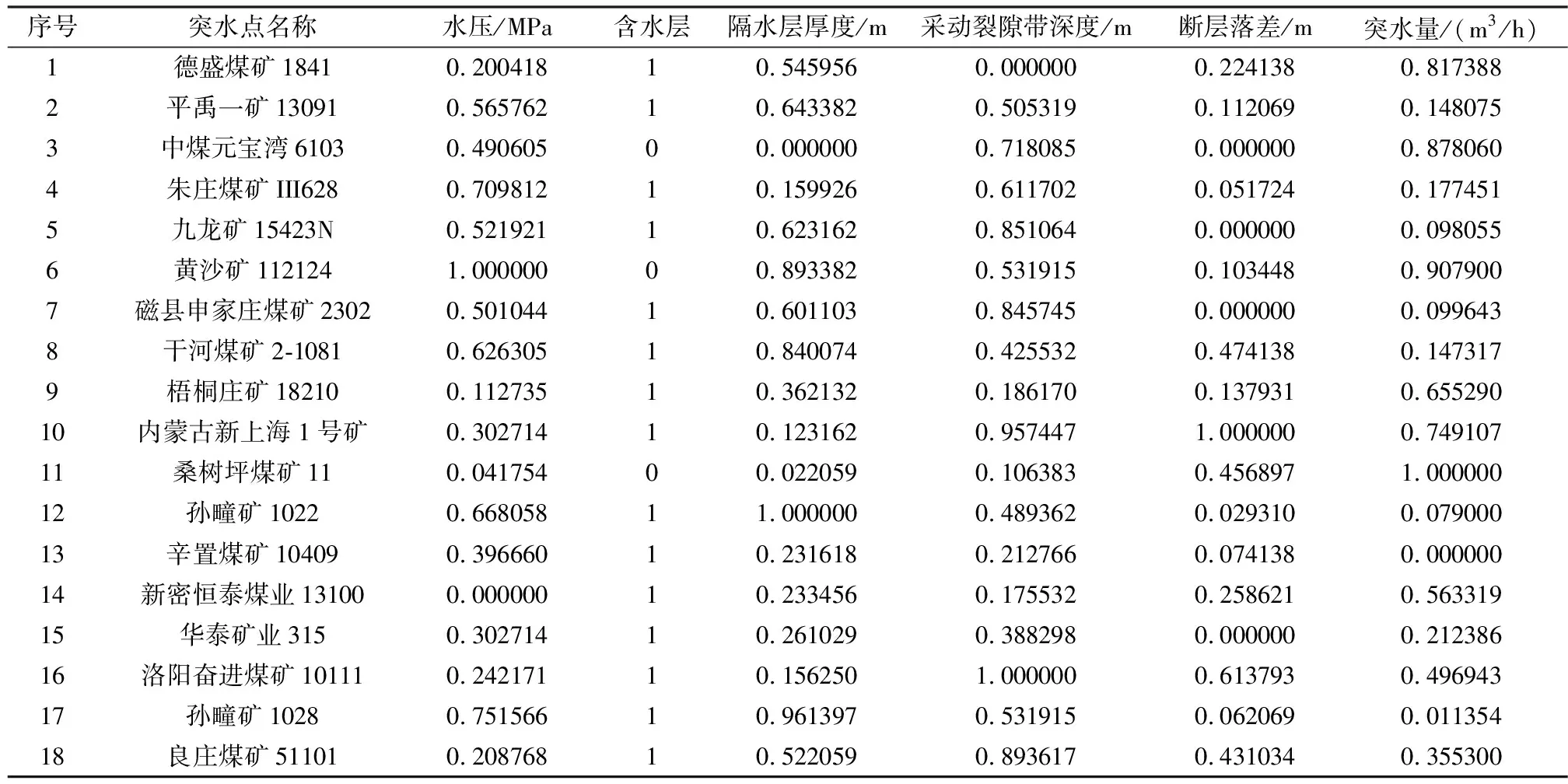
表1 标准化样本集Table 1 Standardized sample set

3.3 参数优化及突水量模型建立

通过Matlab编写程序，设置迭代次数为150，种群规模为35，迭代寻优后果蝇群体中出现最优解,参数寻优之后得到惩罚因子C=83.68、不敏感损失函数ε=0.324和核参数σ=1.8789的预测模型。

3.4 模型验证

通过建立的FOA-SVR模型对预测样本集进行突水量预测，得到预测值之后并对其预测结果进行反归一化，将预测结果及误差分析与通过SVR模型预测出来的做比较，结果见表2。

表2 不同模型预测结果对比Table 2 Comparison of prediction results based on different models

由表2中的预测结果分析可知，FOA-SVR模型对4个预测样本集的预测相对误差分别是2.7934%、2.1330%、6.8556%和1.7994%，用SVR模型的预测相对误差分别是11.5400%、7.2246%、15.9150%和8.9713%，即FOA-SVR模型相比于直接使用SVR模型来说误差更小，预测精度更高。说明果蝇算法选择的模型参数合适，该突水量预测模型具有很强的泛化能力，可以达到预测底板突水量的目的，为煤矿采取合理的防治措施提供依据。

4 结 论

1) 本文选用支持向量回归机模型对底板突水量进行预测，选择水压、含水层厚度、隔水层厚度、底板采动裂隙带深度和断层落差这5个影响因素作为输入因子，输出即为需要的突水量，可以有效地避免定性分析的局限性。

2) 人为去选择支持向量回归机参数的话，会有随机性和盲目性，选择国内一些典型的煤矿突水事故样本集，分为训练样本集和测试样本集两部分，利用FOA模型对样本数据进行训练选择最优参数建立FOA-SVR突水量预测模型，通过该模型对测试集突水量进行预测。通过实验分析验证，该模型比SVR模型具有更高的预测精度。