圆周特征描述:有效的叶片图像分类和检索方法*
2019-05-20黄竹芹陈良宵
王 斌, 黄竹芹, 陈良宵
1(南京财经大学 信息工程学院,江苏 南京 210023)
2(电子商务省级重点实验室(南京财经大学),江苏 南京 210023)
1 引 言
植物是地球生态系统的一个重要组成部分,目前已知的植物种类数量大约在40万左右,还存在大量未被分类或未知的物种.植物的分类识别是生物和环境科学非常重要的一个研究课题,对生物多样性保护,生态农业、生物安全等有着重要的意义.作为植物的六大器官之一的植物叶片,因其方便采集、状态相对稳定,且不同种类植物一般在其叶片的视觉特征上存在着差异,为植物的分类识别提供了非常有价值的线索,是植物分类的重要依据.将计算机视觉技术引入植物分类的一个核心的工作就是对采集的植物叶片图像进行描述,以用于自动地对植物进行分类识别.
一般叶片形状往往存在较大的类内变化,如图 1(a)中给出的属于同一类的 5幅叶片图像,且又有许多叶片形状具有非常小的类间差异、如图1(b)中给出的属于不同类的5幅叶片图像,这些问题的存在给叶片图像的精确识别带来了很大的挑战.如何从叶片图像中抽取具有强辨识能力的图像特征,是解决该问题的关键.本文提出一种圆周特征叶片图像描述方法,通过圆心置于叶片轮廓线上的圆与叶片图像的轮廓线和目标区域分别相交所得到的圆心角、区域像素点在圆周上的分布,以及它们的灰度统计来分别表征叶片图像的轮廓、区域和灰度特征.

Fig.1 Leaf image samples图1 叶片样本的示例
本文的主要贡献在于:
(1) 现有的叶片图像仅从轮廓线、叶片区域或灰度级特征中的某一方面来描述叶片图像,而本文提出的圆周特征描述自然地组合了图像的轮廓线、区域和灰度信息,使其对叶片图像的描述更为全面;
(2) 现有的多尺度方法在轮廓线上各点的尺度安排都是相同的,即它们所采用的各尺度级的尺度大小一般是固定的,并不随轮廓线上点的变化而发生改变,而本文提出的多尺度描述方法是一种具有局部特性的多尺度安排,其各个尺度级的大小,即圆的半径,取决于圆心所在的轮廓点与轮廓线上其他各点的距离,因此,当圆心所在的轮廓点发生改变时,则圆的半径也相应地发生改变,这种有着局部特性的多尺度安排,使得描述子能够更好地抽取到强辨识能力的形状特征;
(3) 本文提出的方法在著名的叶片图像检索测试集 Flavia[1]和叶片图像分类测试集 Swedish[2]上得到的结果要好于目前公开发表的方法在该测试集上报告的最好结果,证明了该方法的有效性.
2 相关工作
在叶片图像描述方面,已提出了许多方法,这些方法可分为基于轮廓线的方法、基于区域的方法和基于灰度级特征的描述方法.基于轮廓线的方法描述叶片图像仅考虑叶片图像的边界像素点[3].其中,最为著名的是Belongie等人[4]提出的形状上下文(shape contexts)描述方法,该方法用原点位于轮廓线上的点的极坐标栅格,来统计轮廓线其他各点相对于该点的空间分布,用产生的直方图构成基于该点的形状描述,称为形状上下文,该方法非常好地描述了轮廓线上的点的空间关系,在形状识别中效果显著.Ling等人[5]在形状上下文的基础上,用轮廓点之间的内距离代替形状上下文算法中使用的轮廓点之间的欧氏距离,这里,内部距离定义为轮廓线上两个点关于目标区域的最短路径长度.内部距离形状上下文(IDSC)方法具有对关节变换的不敏感性.该方法在著名的Swedish[2]叶片图像测试集上取得了94.13%的分类准确率.近来,Zha等人[6]提出了一种引入学习机制的形状上下文描述子.该方法对轮廓线进行不同尺度的高斯卷积,产生多尺度的形状上下文描述子,通过词典学习方法[7]生成形状模式词典,统计一个形状的多尺度形状上下文描述在该模式词典的所有模式上的分布,得到形状的最终描述.因引入了学习机制,该方法具有非常好的形状分类效果,在 Swedish[2]叶片图像测试集上取得了97.07%的分类准确率.
上述方法主要考虑目标轮廓的空间关系,也有更多的方法着眼于叶片轮廓上的曲率特性.经典的方法是Mokhtarian[8]提出的曲率尺度空间方法.该方法用不同宽度的高斯核去平滑曲线,同一尺度下的曲线拐点构成一幅二值图像(称为CSS图像),其中,图像的横轴坐标代表拐点在曲线上的位置,纵坐标代表高斯核的宽度.CSS图像由若干个拱形轮廓组成,每一个关于形状的凸和凹,其最大者构成形状描述.该方法被MPEG-7推荐为标准的轮廓线形状描述.另有一些方法用与轮廓线的曲率特性相关的几何量来生成描述子.Alajlan等人[9]提出了一种带符号的三角形面积表示法来表示形状轮廓的凸凹特性,该方法用顶点位于轮廓线的三角形的面积来描述形状,并用相关的轮廓线的弧长来控制尺度.Mouine等人[10]对该方法进行了拓展,除用三角形面积外,三角的边长、内角等几何量也被用于形状描述.不同于标准的基于微分的曲率计算法,Manay[11]提出了一种基于积分运算的曲率度量方法.该方法用圆心位于轮廓线的圆盘与叶片区域相交的面积来度量轮廓线的曲率.Kumar等人[12]用该方法计算了不同尺度下轮廓线上点的曲率,构成一个多尺度曲率直方图(HoCS)来描述叶片图像,并用该方法开发了一个叶片种类识别系统.近年来,Hu等人[13]提出多尺度距离矩阵描述方法,Wang等人[14]提出多尺度拱高描述,Liu[15]提出基于高斯混合模型的形状描述方法,这些基于轮廓线的描述方法都在Swedish叶片图像测试集上取得了较好的分类效果.
轮廓线描述方法仅从叶片图像的轮廓构造描述子,而另有一些方法将叶片形状区域内所有的像素点作为输入来产生描述子.Du[16]等人提取了叶片图像的不变矩特征[17]和若干个区域度量,包括纵横比、矩形度、凹凸性、偏心率、凸包面积比、凸包周长比等来描述形状.Wang[18]等人用二值叶片图像的7个几何不变矩和16个Zernike矩来描述叶片形状.文献[19]将叶片图像表示为一个2D的二值函数,用基于该函数的2D傅里叶功率谱生成不变的形状描述子,该方法在Swedish测试集上,采用1NN分类器,取得了92.27%的精确率,而采用支持向量机作为分类器,则取得96.53%的分类精确率.文献[20]用快速Curvelet变换得到3个Curvelet系数,对每一个系数,用其第1个不变矩表征叶片形状.
除了利用叶片的形状构造描述子之外,叶片图像的灰度特征也被用来产生描述子.Wu等人[21]用多光谱技术进行绿茶叶片分类.该方法抽取不同波长的绿茶叶片图像的熵值作为纹理特征,用支持向量机(SVM)和径向基函数(RBF)核函数可通过100%的精确度确定茶叶类别.Dalcimar等人[22]使用Gabor小波滤波器在更大的叶片数据集上进行测试,计算每个滤波器响应的能量,识别率达到 84.00%.Chaki[20]采用 Gabor滤波器和灰度共生矩阵(GLCM)提取叶片图像的纹理特征.Tang[23]将非重叠窗口局部二值模式(LBP)和灰度共生矩阵(GLCM)相结合,用于绿茶叶片分类,该方法可通过较低的计算成本有效地提取叶片纹理特征.
上述方法由于仅从轮廓线、叶片区域或灰度级特征中的某一方面来描述叶片图像,在识别率方面并不十分理想.尽管其中一些方法考虑组合叶片形状特征和纹理特征去识别叶片图像,但其算法并不能有效地融合这两类特征,以使叶片图像的识别率得到更大的提升.在文献[24]中,我们首次提出了用圆周与叶片图像相交的几何特性来描述叶片图像,而本文对该想法作了较大的拓展和深化,对3类圆周特征(叶片轮廓、叶片区域和灰度特征)的有效性进行了深入的分析,并提出了一种对这3类圆周特征进行有效融合的方法,实验结果表明,该方法取得了比现有的叶片图像描述方法更高的识别率.
3 圆周特征描述方法
本节提出了一种圆周特征叶片图像描述方法,下面给出该方法的细节.
3.1 图像的预处理及表示
首先对叶片图像进行预处理操作,预处理的步骤如下.
(1) 彩色图像灰度化,这里采用加权平均法,它是图像灰度化最常用的方法,因为由该方法得出的结果更接近人的视觉感知,公式表示如下:

其中,R,G,B表示彩色图像中每个像素点颜色的3个分量,即红、绿、蓝3种颜色,每个分量的取值区间为0~255,因此通过式(1),一个彩色图像被变成灰度图像,将有255个灰度级;
(2) 灰度图像二值化,本文采用Matlab软件中的graythresh函数来计算阈值,该函数实际采用了Otsu算法进行阈值分割,得到的二值图像函数如下:

为方便后面的计算,我们将上述函数变反,即叶片区域像素点的取值为1,反之为0;
(3) 用经典的轮廓跟踪算法提取叶片的轮廓线,再沿顺时针方向将轮廓线均匀采样成N个点 Ω={p1,p2,…,pN},由于轮廓线是闭合的,有pi+N=pi和pi-N=pi.
图2给出了叶片图像预处理的流程.经过上述操作,我们得到了灰度图像s(x,y)、二值图像f(x,y)和均匀采样后的轮廓线Ω={p1,p2,…,pN}.

Fig.2 Flow chart of the leaf image preprocess图2 叶片图像预处理流程示意图
3.2 圆周特征
给定轮廓线Ω上的一个点pi和半径R,我们可以得到一个以pi为圆心,以R为半径的圆,我们用该圆分别提取叶片图像的圆心角特征、圆周积分特征和圆周灰度统计特征.
(1) 圆心角
在该圆与轮廓线Ω的所有交点中,求取与圆心pi(xi,yi)距离最近的两个交点,即从pi点出发,分别按顺时针和逆时针方向,遍历轮廓线所经历的第1个交点,我们将它们分别记为.定义该圆与轮廓线Ω所成的圆心角为以pi为顶点,边绕点pi沿顺时针方向旋转到边,所转过的角,记为,图3给出了圆心角的示例.

Fig.3 The illustration of the central angle feature图3 圆心角示例

我们称该特征为基于轮廓点pi的圆心角特征,其中,为三角形的面积.不仅能很好地描述叶片轮廓的曲率属性,并且不需要对特征值进行额外的规范化处理;当图像发生旋转、平移和缩放时,这3点的相对位置并不发生改变,因此,它们形成的角度大小不变,则圆心角特征具有内在的旋转、平移和缩放的不变性.
(2) 圆周积分
首先计算该圆的周长C=2πR,再在圆周上均匀采样C=round(c)个点,这里,round()表示四舍五入取整,其中,坐标可用下式来计算:
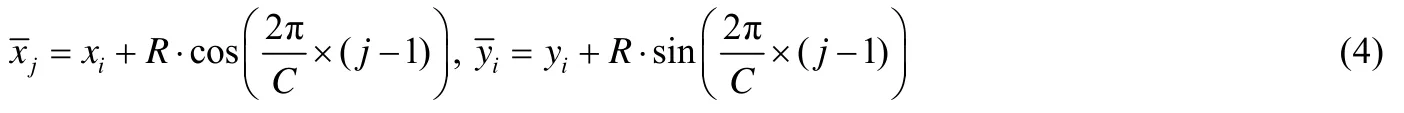


Fig.4 The illustration of the circular integral features图4 圆周积分特征示例圆周积分特征示例
(3) 圆周灰度统计
为便于提取的灰度特征与前面抽取的形状特征组合使用,我们首先将叶片区域的像素点的灰度值用它们的最大值归一到区间[0,1].前面我们已对圆周均匀采样了C个点,其中,j=1,2,…,C,本文对其中落在叶片区域内,即满足的像素点的灰度信息进行统计,得到它们的灰度均值和灰度标准差,定义如下:反映了叶片区域像素点沿圆周的灰度分布的平均水平,而则反映了叶片区域像素点沿圆周的灰度
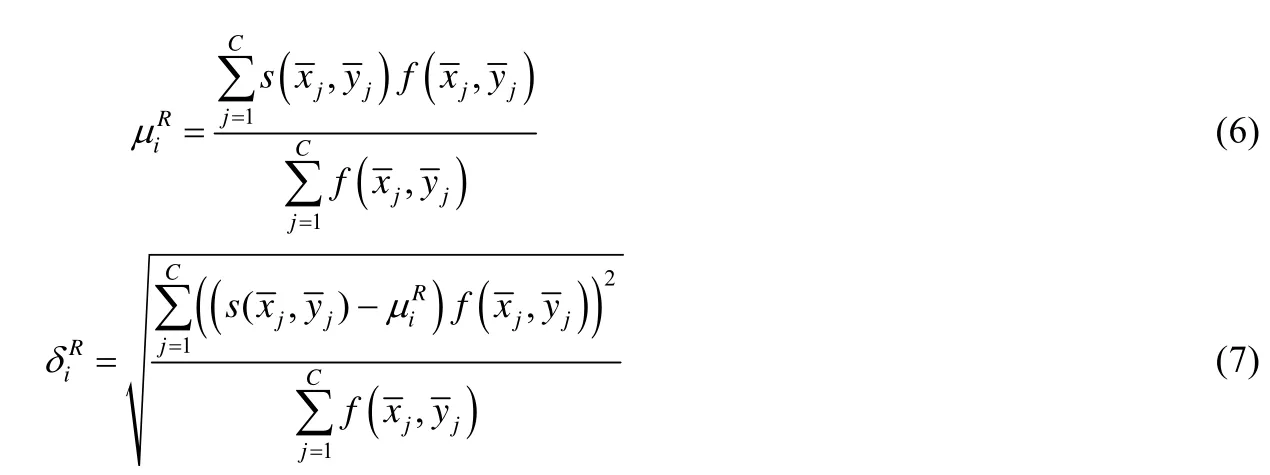
?分布的平均波动强度.根据灰度统计特征的产生机制,其与圆周积分特征一样具有平移、旋转、缩放的不变性.圆周灰度统计特征的示例如图5所示,蓝色点表示圆心,红色部分表示圆周与叶片区域相交的部分.
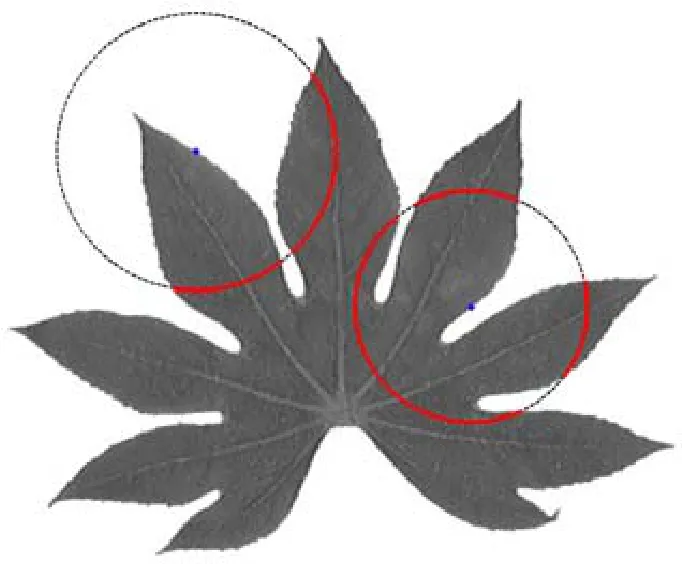
Fig.5 The illustration of the circular gray statistical features图5 叶片图像的圆周灰度统计示例
3.3 多尺度的圆周特征描述
人的视觉系统对目标的视觉感知具有多尺度的特性,多尺度描述方法可以从不同层级描述叶片形状,不但可以提取到叶片图像的全局信息,还能捕捉到叶片图像的局部细节.本文提出的叶片图像的圆周特征具有潜在的多尺度描述能力,通过改变圆的半径R,可以产生多尺度的叶片图像描述.
对于轮廓Ω上的点pi(xi,yi),我们取Ri为该点与Ω中的最远点的欧氏距离的一半,其数学定义如下:

由此确定圆的半径R的取值范围为(0,Ri].我们在该区间内产生如下K个值:

那么以半径作为尺度,并让R分别取上述各值,我们得到了一个具有k级的尺度安排,r0为该尺度安排中的最大尺度,rK-1则为该尺度安排中的最小尺度.需要指出的是,轮廓点改变后,Ri将发生变化,对应的尺度安排也将发生改变,因此,相较于现有的采用固定尺度的方法(它们一般在同一尺度级下,在轮廓各点都取相同的尺度值),该尺度安排具有局部特性.图 6~图 8分别给出多个尺度级的圆心角特征、圆周积分特征和圆周灰度统计特征的示例.
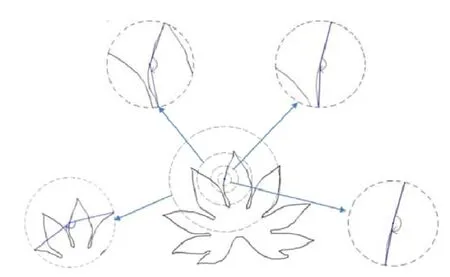
Fig.6 The illustration of the multiscale central angles under four scale levelsr0 ,r1,r2,r3图6 多尺度的圆心角特征的示例,图中给出了在4个尺度级r0、r1、r2、r3下的圆心角
我们用叶片图像的多尺度圆周特征构造描述子.对于每一尺度级rk,让轮廓点索引由1变化至N,得到圆心角特征向量,圆周积分特征向量统计特征向量,以及圆周灰度.
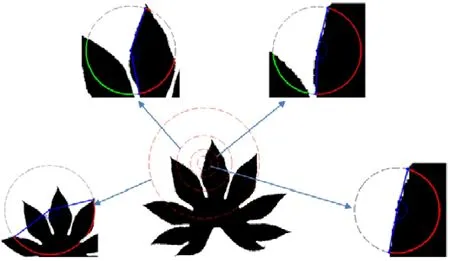
Fig.7 The illustration of the multiscale circular integral features under four scale levelsr0,r1,r2,r3图7 多尺度的圆周积分特征的示例,图中给出了在4个r0、r1、r2、r3尺度级的圆周积分
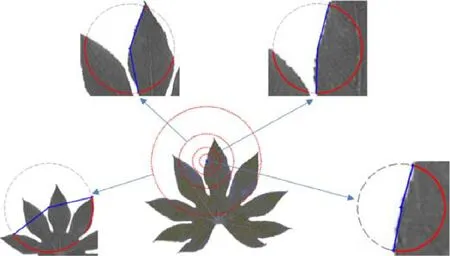
Fig.8 The illustration of the circular gray statistical features under four scale levelsr0,r1,r2,r3图8 多尺度的圆周灰度统计特征的示例图,图中给出了4个尺度级r0、r1、r2、r3的圆周灰度统计特征
如图9所示,我们对给出的3幅叶片图像(其中,a和b属于同一类),绘出了它们的圆周积分特征β在尺度级r0、r1、r2、r3下的曲线,以便观察圆周特征描述子的多尺度特性.图中给出的 3幅叶片图像具有整体形状的相似性,叶片c与叶片a和b的差异性在于其具有边缘锯齿.根据圆周特征的多尺度描述机理,其大尺度描述子对形状的细节不敏感,主要侧重于形状的粗粒度特征,而小尺度描述子则相反,主要刻画形状的细节信息.而观察图像中的4个尺度级r0、r1、r2、r3的特征曲线可以看出,在尺度r0,3幅图像的特征曲线相互之间非常接近,而当尺度逐渐减小(从r0变化到r3),叶片a与叶片b的特征曲线仍然保持相互靠近,而c的特征曲线逐渐远离叶片a和b的特征曲线.从图9给出的特征曲线,可以清楚地观察到圆周特征描述子的这种多尺度行为特性.
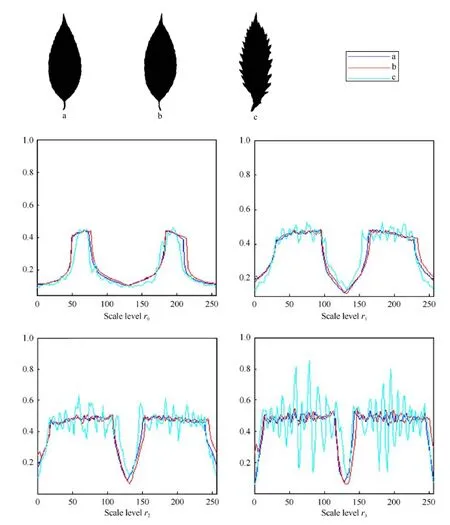
Fig.9 The curves of the circular integral featuresβ under four scale levelsr0,r1,r2,r3 for leaf images a,b and c(leaf a and leaf b blong to the same class)图9 3幅树叶图像a、b、c(其中,a与b为同一类)的圆周积分特征β在尺度级r0、r1、r2、r3下的曲线
需要指出的是,本文提出的圆周特征描述子通过抽取圆心角和圆周积分特征描述叶片的形状,通过抽取圆周灰度统计特征描述叶片的灰度信息.现有的叶片图像识别方法大多仅通过形状特征来进行识别.而本文提出的圆周特征描述子,通过圆周与叶片图像相交的几何特性,有效地组合了叶片的形状特征和灰度信息,从而具有较高的识别能力.我们在图10中给出了一个例子,以进一步说明圆周特征描述子的描述能力.图10给出了3幅叶片灰度图像(a和b属于同一类),从形状上看,它们非常相似,难以区分.图中绘出了这3幅叶片图像的圆心角特征α、圆周积分β、灰度统计特征μ和δ的特征曲线.对于各类特征,图中还给出了叶片a的特征曲线分别与叶片b和叶片c的特征曲线的L1距离,以便于量化比较.从该图可以看出,3幅图像的圆心角特征α、圆周积分β曲线都非常靠近,如果仅依据该两类特征进行识别,就会将叶片a误识别为与叶片c同一类.而观察该图的灰度统计特征μ和δ的特征曲线,叶片a和b的曲线相互靠近,而叶片c的曲线则远离叶片a和b的曲线.说明叶片c有着与a和b显然不同的灰度信息,依据灰度统计特征,叶片a可以正确地识别为与叶片b同属一类.
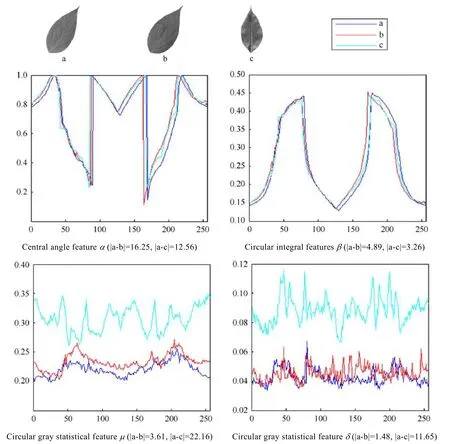
Fig.10 The curves of the central angle featureα,the circular integral featureβ,the circular gray statistical feature μ and circular gray statistical featureδ at scale levelr0 for leaf images a,b and c (a and b belong the same class),|.| denote theL1 distance between two curves图10 3幅树叶图像a、b、c(其中,a与b为同一类)的圆心角特征α、圆周积分特征β、灰度统计特征μ和δ在尺度级r0下的曲线,|.|表示两条曲线的L1距离
3.4 归一化描述
本文提出的圆心角特征、圆周积分特征和圆周灰度统计特征已满足平移、旋转和缩放的不变性,但是由于叶片的轮廓线是一条闭合曲线,任意轮廓点都可以作为轮廓线的起始点,因此为得到归一化的描述,我们仅需将描述子进行始点归一.我们用离散傅里叶变换来完成这一任务.对尺度级rk下的圆心角序列,其离散傅里叶变换为
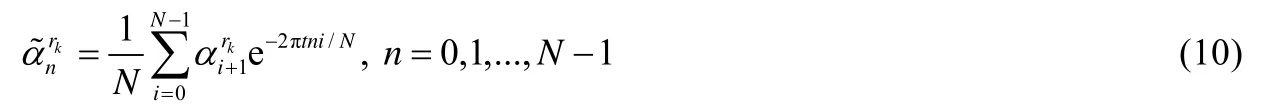
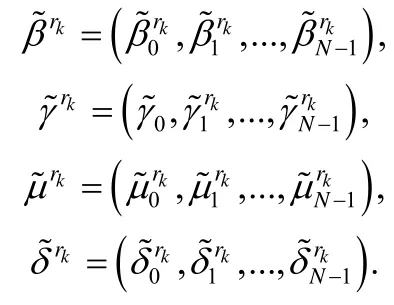
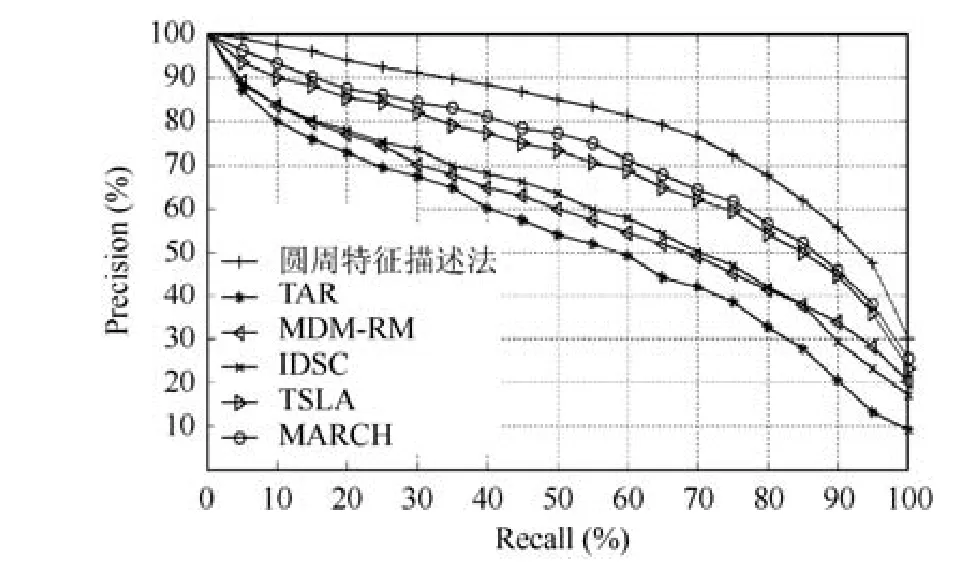
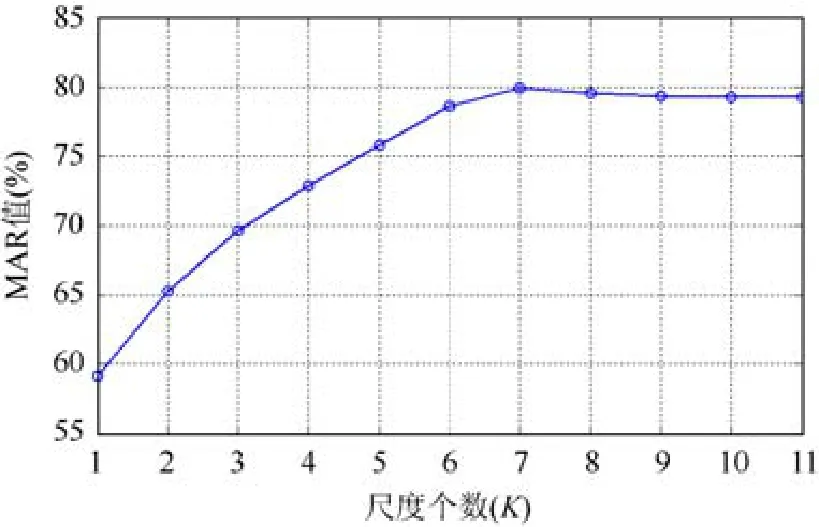
因轮廓起始点的变化仅改变傅里叶系数的相位信息,对于上述傅里叶系数序列,我们只取每个系数的幅度值,同时,为了使描述子更加紧致且对噪声更具鲁棒性,我们取前M个系数(M< 自此,我们得到了完全不依赖于形状的平移、旋转、缩放和轮廓线起始点的5类特征α、β、γ、μ和δ.但这5类特征一般有着不同的数量级,将它们组合使用去完成叶片图像的分类和检索任务,可能会出现某类高数量级的特征在比较中处于支配地位,而使得其他低数量级的特征失效的问题.我们进一步对它们进行数量级的归一.因为本文的工作主要是为了完成叶片图像的分类和检索任务,在分类任务中,我们用训练集中的所有图像,而对检索任务,我们用所有的数据库图像,来对这5类特征进行数量级的归一.这里,我们以执行分类任务对图像的圆周特征描述的α特征的数量级归一为例,阐述其操作步骤如下. (1) 对每一幅训练集图像,计算其α特征的所有尺度的 0阶傅里叶系数的均值,得到训练集图像的索引号; (3) 用Mα对所有的样本(包括训练集和测试集)的α特征向量进行归一,即用特征向量α/Mα替换原来的特征向量α. 对特征μ和δ,我们进行同样的归一化操作.但对特征β和γ的归一化处理稍有不同.由β和γ的定义(见公式(5)),它们同属圆周积分特征,分别计算的是圆周的内弧和外弧与叶片区域相交的长度.用它们各自的Mβ和Mγ去进行特征归一,不能保持内弧积分特征和外弧积分特征的原有比例关系这一有用的信息.为此,在上述归一化操作的第3步,我们用max(Mβ,Mγ)去归一所有样本的β特征向量和γ特征向量.经过上述归一化操作,各类特征将具有同样的数量级,方便在后续形状特征的比较中对它们组合使用.对于执行图像检索任务,处理方法相似,不同的是,执行归一操作时,用的是所有的数据库图像,而不是训练集图像(检索任务没有训练集),用计算的均值对所有样本(包括检索图像和数据库图像)进行归一操作. 给定叶片图像A和B,抽取它们的归一化的圆周特征描述{αA,βA,γA,μA,δA}和{αB,βB,γB,μB,δB}.它们之间的距离定义为 其中,|.|表示L1距离.较小的dis(A,B)表示叶片A和叶片B之间有着较大的相似度,而dis(A,B)越大,则说明它们的差异越大.这里需要说明的是,在圆周特征描述中,圆心角特征α描述叶片图像的轮廓线特征,圆周积分特征β和γ描述的是叶片区域的几何特征,而圆周灰度统计特征μ和δ描述的是叶片图像的灰度特征.因为在描述子中,圆心角特征只有一个特征向量,而圆周积分和圆周灰度特征各有两个特征向量,为保证这 3类特征在特征比较中的特征数的平衡,在公式(16)中,对后两类特征进行了除2处理. 本文的实验平台是一台操作系统为Windows 10、CPU为Intel(R) Core(TM) i5、内存8GB的个人计算机,算法的编程实现工具为MATLAB R2010b.我们通过将本文提出的算法分别应用于叶片图像检索和叶片图像的分类,以验证本文提出的算法的有效性.在实验中,本文提出的算法的参数设置为:轮廓线采样点的个数为256,所用的尺度个数为7,傅里叶变换中保留的傅里叶系数的个数为7. 为了进行叶片图像检索实验,我们选用了著名的Flavia叶片图像测试集[1].该测试集包含32种总共1 907个叶片样本,每类包含50~72个样本,大部分采自中国长江三角地区,如中国七叶树、紫荆、银杏树、广玉兰等.图11给出了每一类的一个样本,由该图可以看出,许多样本在形状特征上具有很大的相似性,为正确区分它们带来了挑战. Fig.11 Image samples of 32 types of leaf samples in Flavia data set[1]图11 Flavia数据集中的32类叶片样本图像示例[1] 已有许多方法[10,13,14,25,26]在该测试集上报告了结果,在实验中,我们采用标准的检索性能评估方法.常见的评估方法有两种,一种是查准率(precision)/查全率(recall)曲线法[10,14],另一种是平均精度均值(mean average precision,简称MAP)法[10,14,19].查准率/查全率定义如下: 这里,n1是一次查询返回的样本的个数,r是返回的图像中与查询图像属于同一类的个数,n2是数据集中与查询图像属于同一类的图像个数.查准率是测量查询的精度,而查全率则是测量从数据集中检索相似形状的能力.以数据集中每一幅图像作为查询样本,与测试集中所有图像进行匹配,即计算它们之间的形状差异度,再根据差异度由小到大,对返回的图像进行排序.对于每一个待查询的形状,令查全率从10%~100%发生变化,并计算所对应的查准率,由此绘出查准率/查全率曲线.这里给定查全率,对应的查准率的计算方法为:根据公式(17),计算出返回图像中与查询图像属于同一类的个数,再在排好序的图像中确定应返回的图像个数,从而计算查准率,最后计算所有查询图像的查准率的平均,得到平均查准率. 对于平均精度均值MAP法,精度均值(average precision,简称AP)定义为 其中,n表示检索中返回的图像的个数,p(j)是前j最佳匹配的准确率,g(j)是标记函数,当第j个最佳匹配与查询图像属于同一类时为1,否则为0,Q表示数据集中与查询图像属于同一类的图像个数.计算出所有查询图像的AP值,求均值后便可得到MAP值. 为了验证本文提出的圆周特征描述法的有效性和优越性,本文选取了近年来发表的 5种具有良好性能的叶片图像检索算法进行比较:三角形面积法(TAR)[10]、多尺度距离矩阵(MDM)[13]、内距离形状上下文(IDCS)[5]、三角形边长角度法(TSLA)[10]、多尺度拱形高度法(MARCH)[14].其中,多尺度距离矩阵(MDM)有多种不同的版本,我们选取的是效果最好的版本.在图 12中,我们绘制了本文提出的算法和其他参与比较的算法的查准率/查全率曲线.从该图可以看出,对给定的每一个查全率,本文提出的圆周特征描述法都取得了比其他 5种方法更高的查准率.当查全率为 5%时,即平均每次查询返回 2~3个与待查询叶片最相似的叶片样本,圆周特征描述法的查准率达到了98.95%,比其他两种最好方法MARCH[14]高和TSLA[10]分别高出了2.62%和5.49%;当查全率达到50%时,即测试集中与待查询样本的同类样本数的一半被返回时,圆周特征描述法的查准率达到84.97%,分别高于其他两种最好方法MARCH[14]和TSLA[10]达7.78%和11.75%.当查全率达到100%时,圆周特征描述法的查准率为29.88%,仍然高于其他参与比较的算法. Fig.12 The precision/recall curves of the proposed circular features description and the other compared methods on the Flavia dataset图12 在Flavia测试集上本文提出的圆周特征描述法和其他方法的查准率/查全率曲线 本文提出的方法和其他5种参与比较的方法的MAP值,均在表1中列出.从该表可以看出,本文提出的圆周特征描述法取得了最高的MAP值79.9%,比方法TAR[10]、MAM-RM[13]、IDSC[5]、TSLA[10]和MARCH[14]分别高出了27.1%、20.8%、20.0%、10.0%、6.9%.值得指出的是,我们查阅了现有的在该测试集上公开报道的MAP值,本文提出的算法所报告的结果是目前的最好结果.以上数据表明,本文提出的算法的检索性能要优于其他叶片图像检索算法. 由于圆周特征描述法是一个多尺度描述子,我们做了另一组实验来研究尺度个数K的选取对实验结果的影响.在实验中,我们让尺度个数由1~11变化,并得到所对应的MAP值,将实验结果在图13中绘制成折线图.从该图可以看出,当仅取一个尺度时,即只取尺度安排中的最大尺度时,MAP值只有 59.2%,说明此时描述能力较弱,此时描述子只能描述出叶片的全局特征.随着尺度个数K的增加,描述的粒度越来越小,捕捉叶片图像的细节特征的能力越来越强,直到K为7时,MAP达到最高:79.9%,而当K再取更大的值时,MAP值并没有继续增长,其原因是,当圆的半径足够小时,圆内所包含的叶片像素点只有圆心甚至一个像素点也没有,此时的尺度级已不具描述能力,因此我们以为取7个尺度级就能很好地完成叶片图像检索任务. Table 1 The comparisons of the MAP value of the proposed circular features description method with the other methods on Flavia data set表1 在Flavia数据集上的本文提出的圆周特征描述法与其他方法的MAP值的对比 Fig.13 The MAP scores of the proposed methods of taking various number of scale levelsKon the Flavia dataset图13 在Flavia数据集上,本文提出的方法在尺度个数K取不同值情况下相应的MAP值 本文提出的圆周特征描述法包括 3类特征:圆心角特征、圆周积分特征和圆周灰度统计特征,为研究它们在叶片图像检索中的贡献,我们做了另外 4组实验:(1) 仅使用圆心角特征α;(2) 仅使用圆周积分特征β+γ;(3)仅使用圆周灰度统计特征μ+δ;(4) 所有特征组合α+β+γ+μ+δ.表 2中给出了该组实验的结果. Table 2 The MAP scores of using various kinds of circular features on the Flavia dataset表2 在Flavia数据集上,使用各类圆周特征描述的MAP值 从表2可以看出,本文提出的圆周特征描述在单独使用某一类特征的情况下,圆心角特征的MAP值最高,达到了 71.91%,检索效果最好,其次是圆周积分特征,MAP值为 60.37%,单独使用圆周灰度统计特征时,MAP为44.97%,而组合所有的圆周特征,MAP达到79.94%.该组实验说明,叶片图像的轮廓线特征在识别中起到的作用最大,区域特征次之,灰度特征再次,这一结果也与叶片的实际识别依据相一致.但这3种特征组合使用可以弥补它们单个使用的不足,如形状非常相似的叶片,再加入它们的灰度特征,将会明显地提高识别效果. 为进行叶片图像分类性能的评估,我们选用了著名的 Swedish[2]测试集.该测试集中样本采自瑞典,其中有15种类,每类有75个样本,总共1 125幅图像.图14对其中的每一类给出了一个样本,它们包括挪威枫、榆树、夏栎、灰桤木、椴树、爆竹柳等. Fig.14 15 speccies from the Swedish leaf dataset[2]图14 Swedish数据集中的15类叶片样本图像示例[2] 现有算法[5,6,10,13-15,19]在该测试集上的分类性能评估方法是:将 Swedish[20]数据集每类 75个样本图像随机分为25个训练样本和50个测试样本,因此总共有25×15=375个训练样本构成训练集,50×15=750个测试样本构成测试集,计算测试集中每个图像和训练集中的每个样本的相似度,并用最邻近分类器(1-NN)进行分类,即得到的与待测叶片样本最相似的叶片图像若与待测样本属于同一类,则认为是一次正确的分类,统计所有测试的正确率记为分类率.在实验中,我们采用与该方法相同的分类性能评估方法.由于测试集和训练集是随机划分的,与现有的算法[5,6,10,13-15,19]一样,我们将实验重复执行10次,取其平均值.本文提出的圆周特征算法的有关参数与在Flavia测试集上的参数相同.为进一步评估本文提出的圆周特征描述方法的分类性能,我们还将基于监督学习的分类器引入该分类实验,将训练集中的样本的圆周特征描述子作为支持向量机(SVM)的输入,用得到的分类器对测试集中的样本进行分类,统计分类率.在实验中,我们所用的SVM程序为文献[27]的作者提供的源代码LIBSVM. 在表3中,我们给出了本文提出的圆周特征描述法在Swedish测试集上,分别采用1-NN分类器和SVM分类器的分类率.为与其他方法进行对比,表3也列出了近年来在该测试集报告了较好结果的其他8种算法,这些方法大都报告了采用 1-NN分类器的分类率,文献[19]中所提方法则报告了采用 SVM分类器的分类率.从该表可以看出,本文提出的方法在Swedish测试集上采用1-NN分类器,取得了98.84%的分类率,已高于其他参与比较的各种方法,值得指出的是,我们查阅了现有的在该测试集上公开报道的分类率,本文提出的算法所报告的结果是目前所见到的最好结果.而采用基于监督学习的分类器SVM,本文所提方法的分类率又比98.84%的分类率进一步提高了0.18%,达到了99.02%.该实验结果表明,本文提出的叶片图像描述方法在叶片图像的分类性能方面优于现有其他方法,证明了本文提出的方法的有效性以及相较于其他方法的优越性. Table 3 Comparison of classification rate of circular features description method proposed in this paper and other methods on Swedish dataset表3 Swedish数据集上本文提出的圆周特征描述法和其他方法的对比 本文提出了描述叶片图像的圆周特征描述方法.该方法通过圆心位于轮廓线的圆,从叶片图像提取了叶片图像的轮廓线特征——圆心角、形状区域特征——圆周积分特征、灰度特征——圆周灰度统计特征,从而比其他方法更为全面地描述了叶片图像,且抽取的特征具有内在的平移、旋转、缩放的不变性.本文所提出的多尺度的描述框架,使得描述子能由粗到细地描述叶片特征.这种对叶片的形状和灰度特征的全面描述和多尺度的安排,使得本文提出的方法具有非常强的叶片识别能力.在著名的Flavia叶片图像测试集上的检索实验和Swedish叶片图像测试集上的分类实验,都获得了比其他现有的叶片图像描述方法更高的精确率,证明了本文提出的算法的有效性.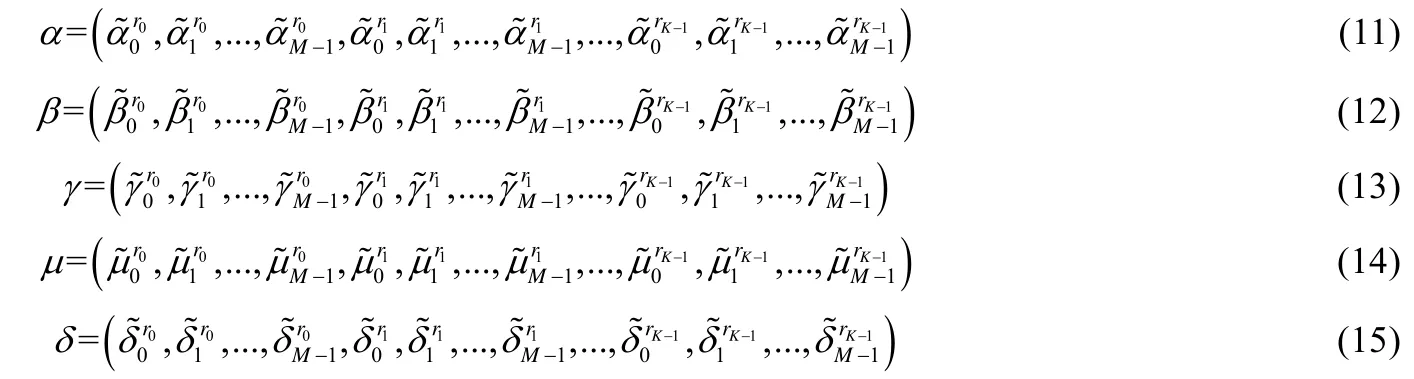
3.5 差异性度量

4 实验结果及分析
4.1 叶片图像检索实验





4.2 叶片图像分类实验


5 结 论
