提高初中数学解题效率的策略

□福建省漳州市第二中学 吴靖

在教学中，学生经常说“数学单调乏味”“听不懂”“听懂了不会做”“数学很难学”等，这类学生普遍特点是对数学语言的转化能力弱，没法理解题目表达的意思，从而数学成绩没法提高，阻碍数学思维能力的发展，所以我认为注重数学语言转化是提高数学解题效率的有效措施。

数学语言作为数学思维的载体，是表达数学思想的通用语言，归结为文字语言、符号语言和图形语言三类。文字语言描述概念、定义、定理；符号语言简明，书写方便；图形语言直观，有利于问题解决。文字语言经常借助图形语言转化为符号语言，是抽象到直观再到抽象的过程。

不同年级的学生对数学语言的理解应用存在很大的差距，初中生对数学语言特别是符号语言没有系统理解或理解浮于表面，审题过程中没有对具体问题具体分析，读不出数学符号隐含的信息，数学符号抽象概括和数学正逆向思维等能力不强，导致数学学习的困难，以下谈谈对数学语言教学中碰到的困难和解决方法。

一、数学语言理解与转化的困难

一个不理解数学语言的学生是不能学好数学的。实际教学中发现很多学生不能很好地理解数学命题，比如把否命题与命题的否定等价，把 4当成了4的平方根等。如多项式x2-ax+1能分解为（x-2)(x+b)，学生没有抓到分解为所要表达的“相等”,又如y=2x和y=ax+4的图象交于点A（m，3）求关于x的不等式2x＞ax+4的解集，部分学生仅仅从形式方面入手，看到关于x的不等式，立刻就归为含参数不等式进行解决，该题需要读懂交点隐含的信息“3=2m和3=am+4”求出a，m的值，最后直接解不等式或通过数形结合等解决。

三种语言的转化可以是文字语言与图形语言的转化，这种转化相对简洁直观。如2019年厦门质检第6题：直角三角形的一条直角边与以另一条直角边为直径的圆相切。符合该命题的图形是（ ）。

解决应用题与命题证明等问题是将文字语言转化为符号语言的过程，是数学问题符号化，将问题数学化的过程。

学生缺少如何把应用题中的文字语言转化为数学符号语言的方法，所以经常看到应用题直接放弃。如：某商店购进甲、乙两种商品，已知每件甲种商品的价格比每件乙种商品的价格贵10元，用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同。

（1）求甲、乙两种商品每件的价格各是多少元？

（2）计划购买这两种商品共50件，且投入的经费不超过3200元，那么，最多可购买多少件甲种商品？

题目中涉及了“商品价格”“商品数量”“商品总价”三个量和“甲”与“乙”两种商品，学生没法抓住他们彼此的联系而造成了困难。

解决这类问题可以借助表格理顺每个量之间的关系，简化题目。问题（1）对于这类“甲比乙贵10元”的类型常假设比后的量；设乙商品每件价格为x元，则甲商品每件价格为（x+10）元；再利用商品件数=得出两种商品数量的符号表示，根据“商品件数”列出分式方程。该题也可以通过间接假设时间列方程求解。

320 x单价x+10总价350数量甲 乙350 x+10 300 x

由问题（1）得出甲商品价格70元，乙商品价格60元，问题（2）则可以假设甲商品a件，进行列表格梳理为：

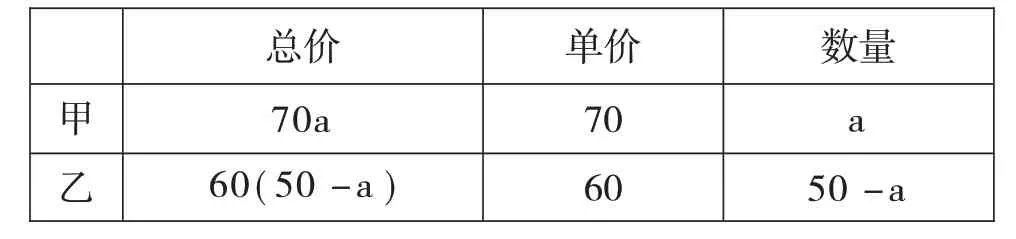
数量a 50-a甲 乙总价70a 60(50-a)单价70 60

借助表格有助于学生梳理应用题，快速理解各个量间的基本关系，有利于将实际问题数学化，故而在平常教学中教会学生列表格分析问题是十分有用的思维工具。

命题证明是近几年福建省中考的热点，命题证明需要将其写成“已知、求证、证明”的模式。2018福建中考第20题求证：相似三角形对应边上的中线之比等于相似比。大部分学生没法将文字语言和符号语言转化，得不到有效的已知条件。在教学中应让学生体会图形语言是文字语言与符号语言的中介，体会三种语言的密切联系。

二、初中数学语言的教学策略

教师引导学生学习，他们对数学语言的教学是否重视很大程度上影响学生的学习态度。在教学中使用规范、科学的数学语言，让学生感受数学的严谨性，引导学生在解题过程中理解掌握符号语言。

培养学生的符号意识，增强学生的数感目的在于让学生应用数学语言解决实际问题，我们可以应用一些方式为学生创设解决问题的情境，让他们有机会使用数学符号。如教学《探索两直线平行的条件》时可以通过照片的摆放位置让学生描述“歪了”，体会用符号语言描述生活中的词语，进而引出如何表示照片“正了”，如何用数学中的几何元素判断照片“正了”。

我们可以借助学生的生活环境和生活常识，结合数学知识点设计问题情境，引导学生利用符号语言描述问题，这是将生活实际问题抽象成数学问题的前提，即数学建模的必要步骤。借助生活实际能够让学生真正体会到符号的意义与价值，感受符号语言的魅力，从而在思维深处产生学习的积极性与主动性。

最后，教师在平常教学中可以尝试对题目语言的描述方式进行改变，改变题目的语言描述方式是习题变式的一种方法，也是近几年考试的重点。文字、图形、符号三种语言的灵活转换可以提高学生的读题能力，培养学生的符号意识，也锻炼了他们对数学语言的应用能力。如：一次函数y=mx+n的图象经过点A（1,0）和B（0,-4）,求关于x的方程 -mx-n=8 的解。

变式：整式mx+n的值随x的取值不同而不同，下表是当x取不同值时对应的整式的值，则关于x的方程-mx-n=8的解为（ ）。

A.x=-1B.x=0 C.x=1 D.x=2

x 0 mx+n-1-8-4 1 0

数学符号语言充满形式化，不能偏重于符号语言的纯形式化，经常通过向其他语言的转化改编题目，可以打破思维定势，提供新的视觉情境，给人一种“柳暗花明”的感觉。

三、结语

初中数学符号语言不同于其他科目的知识，它是灵活的，所以在教学中要遵循学生的认知特点，从定义、基本公式、定理、运算入手，巩固双基。学习新的数学符号语言时，可以通过“以旧引新”或“以新归旧”让新旧符号语言更好对接，体会新旧知识间的异同，久而久之学生对符号语言就会产生“词感”。