圆柱面配合对柔性转子稳定性的影响

曾 瑶，陈 亮，蒋云帆，庞燕龙，吴 凡

(中国航发四川燃气涡轮研究院，成都610500)

1 引言

在现代旋转机械轻质、高速设计趋势下，转子系统的振动问题日益突出，而其中失稳现象更是成为困扰工程师们的难题[1-4]。引起转子系统失稳振动的因素很多，常见的有油膜力、密封力、转轴的刚度不对称、转轴材料的粘性特性、转静碰摩、充液转子和裂纹转子等。转子系统失稳振动一旦出现，将引起支撑失效、转轴断裂等严重故障，甚至造成机毁人亡的恶性事故。

针对转子系统的失稳特性，国内外学者进行了大量研究。Samantaray等[5]发现非线性内阻尼会导致转子系统在某些转速范围内失稳；程礼等[6]建立了考虑结构阻尼的转子动力学简化模型，采用Routh Hurwitz判据和平衡点解预测追踪算法分析了转子系统的失稳门槛转速；高腾等[7]对花键连接转子系统的稳定性进行了研究，采用有限元方法建立了花键连接转子模型，采用特征值方法对花键连接转子系统稳定性进行了分析。但就现有的转子系统失稳振动研究中，鲜有针对配合因素引起的失稳研究。然而工程实际中，因配合因素引起的转子失稳现象并不少见，航空燃气涡轮发动机、直升机传动系统、航天飞机主机供油泵和供氧泵等转子系统均在研制过程中出现过失稳现象[6-11]。为此，本文针对圆柱面配合对转子稳定性的影响机理进行研究，分析各参数对转子稳定性的影响规律，以期为转子稳定性设计提供指导。

2 考虑内摩擦力的动力学模型

航空发动机中常采用热套配合来固联盘和轴、盘和鼓或轴承内环和轴，这些均属于过盈配合。采用过盈配合时，当部件发生变形或受热不均匀时，配合面紧度可能会减小，导致配合面相对滑动而产生内摩擦力。为说明圆柱面配合产生内摩擦力的机理，取图1所示的简单对称转子作为分析模型，其中盘与转轴之间采用圆柱面过盈配合。图中，m为盘质量，d为盘直径，b为圆柱配合面长度，k为转轴刚度，r为转轴直径，l为转轴跨距，T为配合面剪力，M为外力矩，F为横向集中力。

图1 圆柱面配合的简单转子Fig.1 The simple rotor with cylindrical fitting

由图1可知，当轴发生挠曲变形时，转轴中性面外部纤维拉长，内部纤维缩短，轴和盘的配合面产生微变形，盘上配合面会向轴配合面施加阻碍这种变形的剪切力[9]。当轴挠曲变形增大到一定程度，配合面间会出现微滑动，产生内摩擦。在弹性线形状一定的情况下，转轴的曲率正比于挠度，配合面相对滑动速度正比于该处轴的相对速度[12]。配合面剪力为：

式中：FN=σpπrb为配合面挤压力，σp为发生挠曲变形时配合面上的挤压应力；ζ̇c为配合面间相对滑动速度；μ为摩擦系数。

由于上下半轴配合面上所受的剪力大小相等、方向相反，构成一力偶，可以用两个等效的外力矩代替[12]。依据能量等效性原则，可将外力矩对转子产生的作用等价为一个横向集中力，有：

在分析系统的运动稳定性问题时，为便于数学处理，将横向集中力等效简化为线性阻尼力，如式(4)所示。

式中：ci为内阻尼系数。

对于图1所示的简单对称转子，考虑内摩擦力，不计重力作用，在以角速度ω旋转的坐标系Oξηz中，其运动方程为：

通过固定坐标系Oxyz与旋转坐标系Oξηz之间的对应关系

可将运动方程转化到固定坐标系

把复向量方程转换为实变量方程组

其中刚度矩阵可分解成对称部分和反对称部分

由此可见，内阻尼产生反对称交叉刚度分量，且此刚度分量与转速相关。反对称交叉刚度将向转子输入能量，当反对称交叉刚度增大到某一临界值时，系统动力不稳定。

3 稳定性分析

以单盘试验转子为对象进行稳定性分析。其中，盘与轴之间采用过盈配合，转子系统的初始计算参数如表1所示，理论计算得到转子系统的一阶临界转速为205 rad/s。

表1 计算参数Table 1 Calculation parameters

不计重力作用，通过四阶Runge-Kutta法求解转子系统的动力学方程，将微分方程转换为式(11)、式(12)的形式，通过Matlab编程计算，对转子系统的振动响应进行分析。

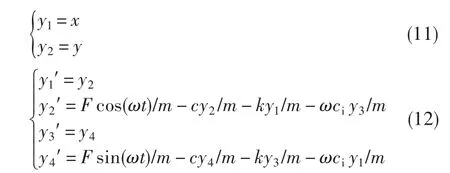
图2 不同转速下的转子响应Fig.2 The rotor response at different speeds

由微分方程求解得到的不同转速下的转子响应。300 rad/s和420 rad/s转速下的转子响应(图2)中，频谱图上存在明显的次谐波，且其频率为33 Hz，与转子系统的一阶临界转速接近，为配合面摩擦产生的内摩擦力所激起的振动频率。转速为300 rad/s时，转子振动响应幅值随时间逐渐降低，转子系统稳定。当转速达到420 rad/s时，时域波形图上振动幅值随时间的增加而增大，频谱图上配合面内摩擦激起的振动成分远超过基频且明显占优，转子发生失稳振动。因此，420 rad/s为转子系统的失稳门槛转速，约为转子系统一阶临界转速的2倍，失稳振动频率为转子一阶临界转速对应频率。

3.1 配合参数的影响

工程实际中，对于配合面的选择，主要参数为配合面的长度和紧度。为此，主要分析配合面的摩擦系数、长度和紧度对系统稳定性的影响规律，分析的前提是配合面之间已经存在相对滑动。

根据图3～图5中的计算结果可以发现：转速ω=420 rad/s时，增加配合面的摩擦系数、长度和紧度，转子系统的稳定性将下降。当摩擦系数由0.1增加到0.2，或配合面长度由19.0 mm增加到20.0 mm，或配合面紧度由100 kPa增加到200 kPa时，转子由稳定变为不稳定，即转子的失稳门槛转速降低；内摩擦力激起的振动频率始终保持在33 Hz左右，不随配合参数的变化而变化。表2总结了配合参数对转子系统稳定性的影响。

需说明的是，针对由圆柱面过盈配合引起的转子失稳振动，圆柱面配合的紧度、长度是非常特别的因素。图3～图5总结的影响规律是在配合面已存在内摩擦的前提下得出的，而实际上配合面间是否存在内摩擦，配合面的紧度、长度是关键参数。当配合面的紧度不足、长度较短时，配合面间可能会产生相对滑动，进而产生不稳定力。当配合面的紧度、长度足以保证配合面间不产生相对滑动时，这一不稳定因素也就不再存在。因此，工程实际中，应合理选择配合面的紧度、长度，防止配合面相对滑动，提高转子稳定性。

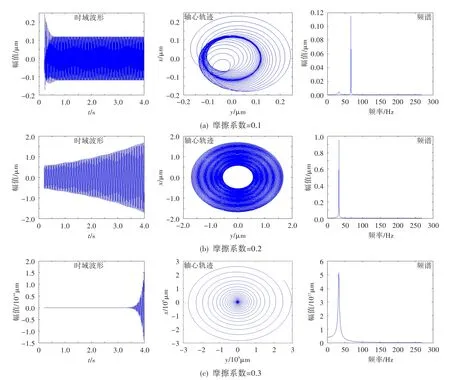
图3 摩擦系数对转子稳定性的影响(ω=420 rad/s)Fig.3 Effects of friction coefficient on rotor stability

图4 配合面长度对转子稳定性的影响(ω=420 rad/s)Fig.4 Effects of fitting surface length on rotor stability

表2 配合参数的影响Table 2 Effects of fitting parameters

3.2 阻尼的影响

图6给出了转速420 rad/s时外阻尼分别为50、100、200 N·s/m时的转子响应。可见，当外阻尼为50、100 N·s/m时，振动响应幅值随时间逐渐增加，转子系统不稳定；当外阻尼达到200 N·s/m时，转子系统振动响应趋于稳定。这表明，增加外阻尼能提高转子失稳门槛转速，降低振动响应幅值，有效提高转子系统的稳定性。表3总结了阻尼对转子系统稳定性的影响。

4 结论

图5 不同配合面紧度对转子稳定性的影响(ω=420 rad/s)Fig.5 Effects of fitting surface compactness on rotor stability

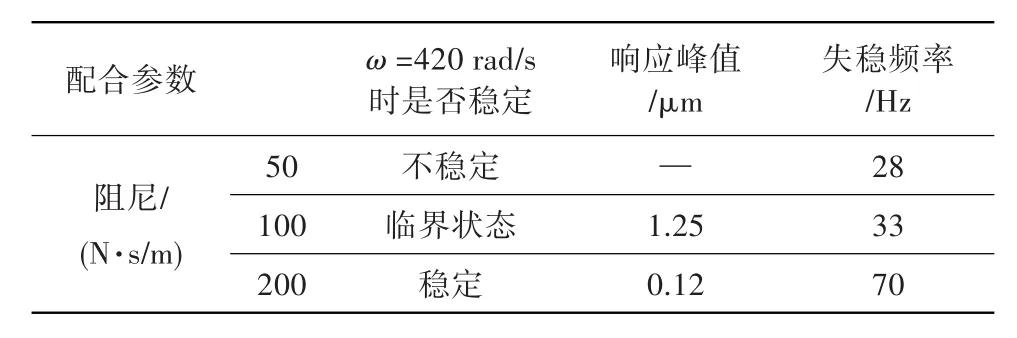
表3 阻尼的影响Table 3 Effects of damping

为研究圆柱面配合产生的内摩擦力对转子稳定性的影响，建立了转子运动微分方程，解释了圆柱面配合对转子稳定性的影响机理；通过直接积分中的Runge-Kutta法对转子系统的稳定性进行计算，分析了各参数对转子稳定性的影响规律。结果表明：

(1)圆柱面过盈配合产生的内摩擦力可以等效为内阻尼力，内阻尼系数进一步分解出反对称交叉刚度分量，引起转子系统的不稳定。

(2)当圆柱面配合处存在内摩擦时，增加配合面的摩擦系数、长度和紧度会降低转子系统的稳定性，增加外阻尼可提高转子系统的稳定性。

(3)配合面的长度和紧度作为由圆柱面过盈配合引起的转子失稳振动中的重要因素，决定了转子是否存在不稳定因素；合理选择配合面参数，可有效预防因结构阻尼引起的转子失稳振动。

图6 阻尼对转子稳定性的影响(ω=420 rad/s)Fig.6 Effects of damping on rotor stability