基于Dragon与Donjon程序的液态熔盐实验堆临界计算与分析
2019-05-17贾国斌伍建辉陈金根顾国祥蔡翔舟
贾国斌,伍建辉,陈金根,顾国祥,蔡翔舟,戴 叶,2
(1.中国科学院 上海应用物理研究所,上海 201800;2.中国科学院 先进核能创新研究院,上海 201800;3.中国科学院大学,北京 100049)
液态熔盐堆是第4代先进核能系统中唯一使用液体燃料的反应堆,与燃料固定于组件的固态反应堆不同,熔盐既作为冷却剂又作为燃料,充满整个一回路(含堆芯)。熔盐堆有多种设计堆型,按堆芯中维持链式裂变反应的平均中子能量不同,可划分为以法国与俄罗斯分别提出的MSFR[1-4]与MOSART[5]为代表的熔盐快堆,以及以美国橡树岭国家实验室(ORNL)提出的MSRE[6]与MSBR[7]为代表的熔盐热堆。熔盐快堆通常使用罐式结构,活性区无慢化剂,堆芯结构简单。熔盐热堆一般采用石墨构件作为慢化剂,并采用镍基合金对其进行固定,控制棒组件根据需要可布置在活性区或侧反射层中。相对于熔盐快堆,熔盐热堆具有更复杂的几何结构。钍基熔盐堆核能专项[8]设计的2 MW液态熔盐实验堆为典型热堆,出于安全与测试需要,堆芯内布置了较多的反应性控制设备与监测孔道,从而对中子学计算工具提出了更高的精确建模要求。蒙特卡罗程序具有精确的几何建模功能,典型的程序如美国爱达荷国家实验室(INL)开发的MCNP[9]、美国ORNL开发的SCALE[10]以及清华大学研发的RMC[11]等。由于以上蒙特卡罗程序可进行精确三维几何建模,可靠性高,目前钍基熔盐堆(TMSR, Thorium-based Molten-Salt Reactor)核能系统专项中子学设计主要基于蒙特卡罗程序。但此类程序的计算成本较高,相对而言确定论程序可显著降低计算成本,进而极大缩短堆芯设计参数的优化时间,是反应堆物理分析的重要模拟工具。
目前,针对含有控制棒及实验孔道等复杂几何组件的液态熔盐堆开展的确定论程序等效建模与适用性分析等较少,但对包含控制棒组件的轻水堆与重水堆已进行了较多的均匀化分析。加拿大蒙特利尔技术学院利用超组件方法[12-13]对重水堆CANDU堆芯中具有特殊结构形式的控制棒组件进行了三维建模与均匀化。西安交通大学在对轻水堆堆芯围板和反射层进行宏观群常数加工时[14-16],采用不连续因子方法确保模型均匀化前后反应率与面净流守恒,计算所得到的堆芯内部功率分布相对偏差小于5%,临界硼质量分数相对偏差小于5×10-5。清华大学[17-18]通过使用不连续因子,对侧反射层中包含控制棒的组件进行了均匀化,计算得到的控制棒与吸收球价值和输运计算所得到的基准解相近,最大绝对误差约为0.001。上述研究表明,不连续因子的使用可显著提高计算精度,但需相应输运程序与扩散程序的支持。
本文基于加拿大蒙特利尔技术学院研制的反应堆物理数值计算确定论程序Dragon[19-20]与Donjon[21],对TMSR专项的液态熔盐实验堆(2 MWth)堆芯进行等效建模与分析。
1 计算模型与方法
1.1 计算模型
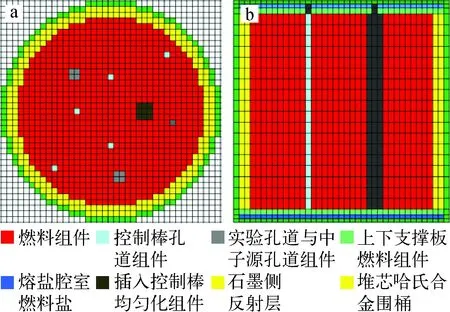
液态熔盐实验堆的堆芯如图1所示。堆芯由活性区的燃料组件、上下熔盐腔室、镍基合金及石墨反射层组成。图1中红色为石墨慢化剂,蓝色为燃料盐,绿色为镍基合金,黑色为控制棒。堆芯活性区包含1个中子源孔道,8个实验测试孔道(分成2组,每组含有4个实验孔道),6个控制棒孔道。控制棒孔道径向位置如图1b所示,其中1号(rod 1)与6号(rod 6)控制棒为调节棒组,3号(rod 3)、4号(rod 4)、5号(rod 5)控制棒为补偿棒组,2号(rod 2)控制棒为紧急停堆棒。为了展示控制棒在堆芯轴向上的上限位与下限位,图1中将4号控制棒插入堆芯并处于下限位,其他控制棒处于上限位。可看出,下限位在下熔盐腔室镍基合金的正上方,上限位在上熔盐腔室与燃料组件之间的镍基合金内。堆芯主要参数列于表1。

a——纵截面;b——横截面图1 液态熔盐实验堆堆芯几何结构Fig.1 Core configuration of liquid molten salt experimental reactor
熔盐堆活性区的方形组件边长为5.1 cm,按照内部结构不同分为4种类型,分别为燃料组件、实验孔道与中子源孔道组件、控制棒孔道组件、控制棒插入孔道组件,其详细几何参数如图2所示。燃料组件的熔盐孔道为带有圆弧的扁长方形。实验孔道与中子源孔道组件为镍基合金同心圆环,四周为燃料盐,中子源孔道与实验孔道纵向贯穿整个堆芯活性区。控制棒孔道的中心小圆环为镍基合金,为控制棒的移动起导向作用。控制棒材料为Gd-Al合金,为同心圆环结构。
1.2 计算工具与组件等效模型
本文使用传统的两步法进行分析,利用加拿大蒙特利尔技术学院开发的反应堆物理数值计算程序包进行计算。首先使用Dragon进行组件计算,得到少群均匀化群常数(组件均匀化),然后使用Donjon进行宏观群常数的插值与全堆扩散计算。扩散计算时调用程序包中Trivac程序[22]的本征值求解模块进行三维扩散计算,最后使用Donjon的功率输出模块给出全堆的三维功率分布。

表1 液态熔盐实验堆堆芯的主要参数Table 1 Key parameter of core of liquid molten salt experimental reactor
为使扩散计算得到的堆芯有效增殖因数及功率分布与蒙特卡罗计算条件一致,均匀化前后需保证堆芯不同区域内、不同反应道的反应率守恒[23]。少群常数计算公式为:

a——燃料组件;b——实验孔道与中子源孔道组件;c——控制棒孔道组件;d——控制棒插入孔道组件图2 组件分类Fig.2 Assembly classification
其中:Σx为x类型宏观群常数;τ为反应率;VⅠ为均匀化Ⅰ区的体积;ФⅠ为均匀化区VⅠ的平均中子通量;V为均匀化区间的体积;r为均匀化区间的几何坐标;E为中子能量;Ф为中子通量。
对中子吸收截面较大的部件,如控制棒组件与用于固定石墨组件的镍基合金,使用超组件方法将周围的燃料组件包含在一起整体均匀化得到1组群常数。本文根据堆芯内不同区域的几何特征,将其分为6种组件,等效均匀化模型如下。
1) 燃料组件
由于中子输运程序Dragon不能处理带有圆弧的熔盐孔道,将弧形熔盐孔道等效为等面积的长方形熔盐孔道。等效方法为保持孔道的宽度(0.417 cm)与面积不变,按照单个熔盐孔道等面积的方法计算,得到孔道长为2.364 4 cm。使用Dragon程序中GEO模块下的两维CAR2D几何模型,将燃料组件分为5×5的两维几何结构,如图3所示,其中红色为石墨,蓝色为燃料盐。为了将4个熔盐孔道划分为单个区域的材料,将石墨组件划分为21个区域。
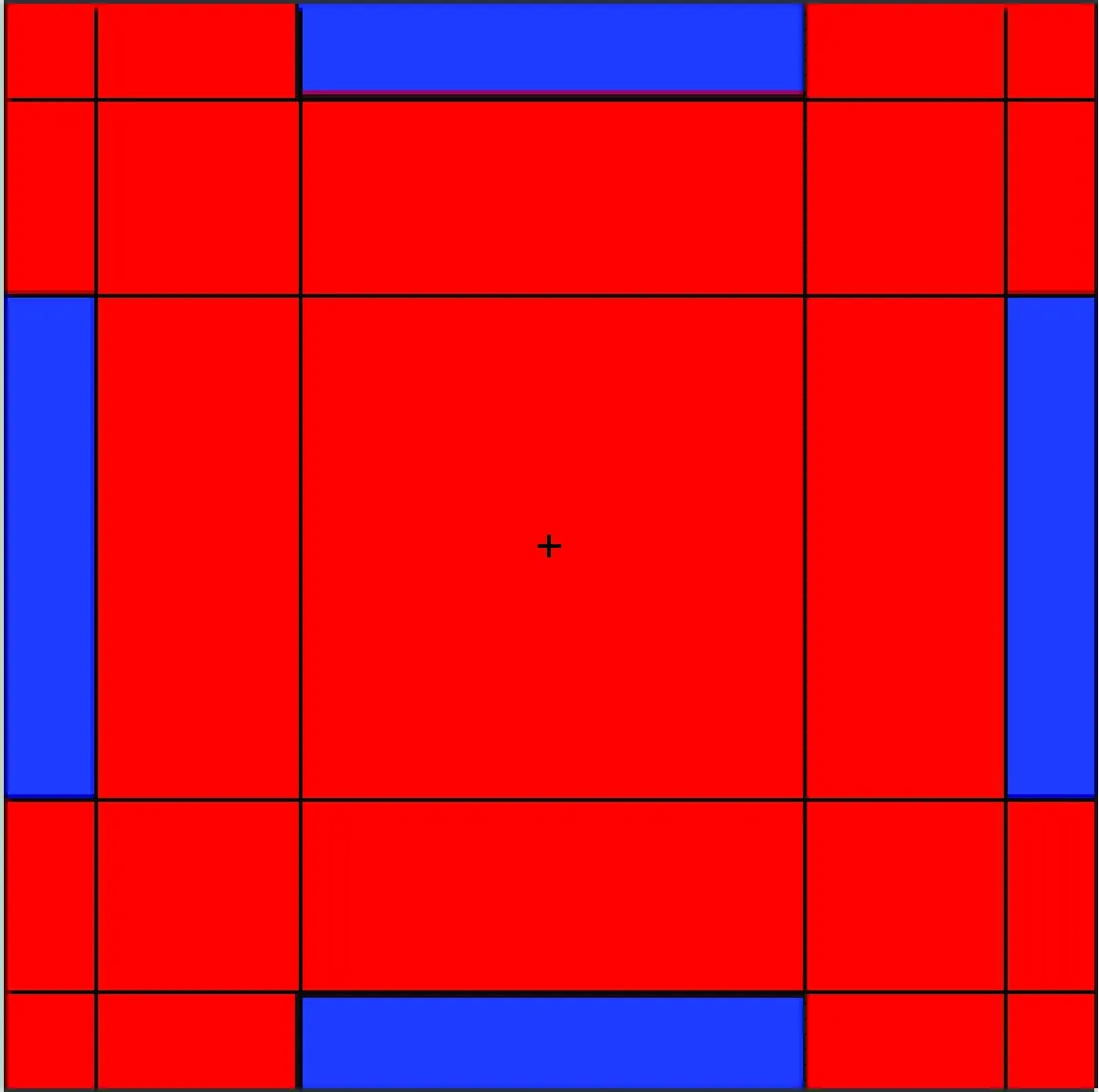
图3 燃料组件均匀化模型Fig.3 Homogenization model of fuel assembly
2) 实验孔道与中子源孔道组件、控制棒孔道组件
实验孔道与中子源孔道组件、控制棒孔道组件都具有规则几何形状,因此使用Dragon程序的CARCEL模块进行精确建模与均匀化,得到相应组件群常数。
3) 控制棒插入孔道组件
对控制棒插入孔道组件进行少群常数加工时,考虑其对周围燃料组件能谱影响较大,使用超栅元方法将包围控制棒的临近8个燃料组件与控制棒组件同时进行均匀化,均匀化后得到一种材料的少群常数。计算模型如图4所示,其中红色为石墨,蓝色为熔盐管道,黄色为控制棒,绿色为镍基合金。燃料组件中熔盐孔道同样等效为等体积的矩形结构,使用Dragon程序GEO模块下的两维CAR2D单独进行建模,中心的同心圆环控制棒使用CARCEL单独精确建模,最终通过CELL模块将以上二维模型进行组合。
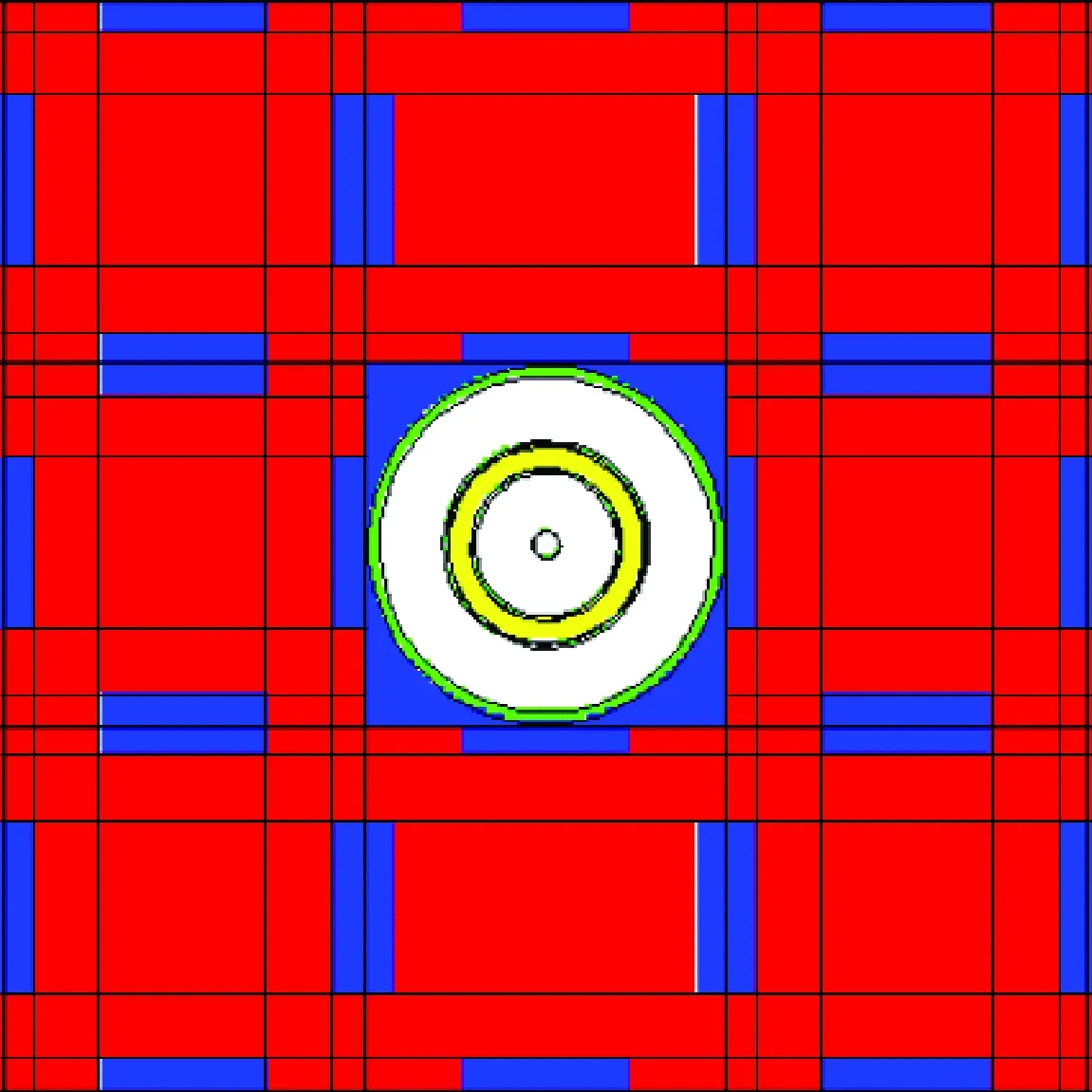
图4 控制棒插入孔道组件的均匀化模型Fig.4 Homogenization model of control rod assembly with control rod inserted
4) 上下熔盐腔室
堆芯的上下熔盐腔室内部为燃料盐,外部使用镍基合金进行燃料盐的包容。尽管此区域的几何模型复杂,但中子泄漏较大且不含慢化剂,因此该区域裂变功率较低,可根据燃料盐的等体积方法进行建模。由于用于固定石墨组件的镍基合金中子吸收截面较大,因此使用三维几何结构进行建模,计算模型如图5所示。其中,石墨燃料组件高度为30 cm,用于包容熔盐腔室的镍基合金使用实际设计的厚度参数3 cm,通过熔盐等体积的方法,得到熔盐腔室内的熔盐等效高度为3.86 cm。用于固定石墨组件的镍基合金使用实际设计参数,高度为5 cm。由于Dragon程序在组件均匀化时无法准确处理真空边界条件(采用真空边界时,共振自屏计算选择等效处理SHI模块时会报错;如选择子群共振USS模块,计算所得到的群常数与蒙特卡罗统计算出的截面相差较大),从而本文采用全反射边界条件进行模拟。为考虑中子泄漏对能谱的影响,使用强中子吸收体10B等效容器外的真空,同时为了将逃逸出堆芯容器的中子全部吸收,保守计算使用厚度为50 cm的10B进行等效。以上模型使用Dragon程序中的CELL模块进行三维建模。

图5 上下熔盐腔室组件均匀化模型Fig.5 Homogenization model of top and bottom molten salt chambers
5) 上熔盐腔室的控制棒
上熔盐腔室中控制棒的均匀化模型与上下熔盐腔室的基本相同,使用三维立方体几何模型。其中包含石墨燃料组件、用于固定石墨组件的镍基合金、经过等效的熔盐腔室中的熔盐(内含控制棒)、外侧镍基合金和使用强吸收体等效的外界真空。使用Dragon程序中的CELL几何模块进行三维几何建模。
6) 侧反射层
为了得到侧反射层石墨的能谱,均匀化模型使用两维模型,将堆芯径向方向上靠近石墨的两个燃料组件与石墨反射层、镍基合金包壳进行均匀化。同样为了考虑中子泄漏对镍基合金的影响,外侧真空使用厚度为50 cm的强吸收材料10B进行等效。以上使用Dragon程序中的CELL几何进行两维建模。均匀化后得到反射层石墨组件,用于包容侧反射层石墨的镍基合金两种材料的少群常数。
对以上6种类型组件进行群常数加工时,使用Dragon程序中的NXT碰撞概率模块、USS子群共振模块以及FLU模块中传统的基模修正B1模型与输运修正PNL模型求解扩散系数。同时,在对补偿棒组(3~5号控制棒)与控制棒全部插入计算分析时,首先使用基模修正获得堆芯keff,然后再将此值代入到输运方程中进行泄漏修正[13],程序计算流程与详细理论公式参考Dragon说明书[20]。
堆芯扩散模型使用等间距划分的网格模型。堆芯径向的网格为边长5.1 cm的正方形网格。对于轴向,活性区的石墨燃料组件网格高度为10 cm,用于固定燃料组件的镍基合金、上下熔盐腔室、包容上下熔盐腔室熔盐的镍基合金的网格高度分别为5、3.86与3 cm。当堆芯单独插入2号控制棒时,全堆扩散的堆芯模型如图6所示。由图6可看出,组件均匀化后的几何模型与实际堆芯模型(图1)的不同之处主要在上下熔盐腔室部分,即将圆弧形上下熔盐腔室的几何结构等效为等体积的长方体结构;其次,活性区与侧反射层交界面处,离散为不连续的矩形结构。
a——堆芯径向;b——堆芯轴向图6 堆芯均匀化模型Fig.6 Homogenization model of core
本文采用Dragon程序进行输运计算时使用能群数为361群的精细群结构,选用ENDF/B-Ⅶ.1的微观数据库,从而保证与本文用于验证计算的蒙特卡罗程序MCNP5的数据库类型相同。考虑到液态熔盐实验堆与高温气冷堆的石墨慢化能力对快中子的慢化与热中子的向上散射能力类似,在进行少群能群结构划分时,重点参考美国宾夕法尼亚大学对高温气冷堆PBMR[24]分析时采用的能群结构[25]。同时考虑到液态熔盐中19F与6Li在10~100 keV及100 keV~1 MeV能区范围内存在共振弹性散射峰,以及初始临界堆芯中无Pu元素,本文在其能群结构基础上进行优化整理,能群结构列于表2、3。由于PBMR控制棒的组分为B4C,而本文计算的液态熔盐实验堆控制棒组分为Gd-Al合金,为了充分考虑155Gd在2.0 eV与2.6 eV附近的共振吸收峰,分别使用两种快热能群分界(2.38 eV与3.93 eV)开展初步敏感性分析。
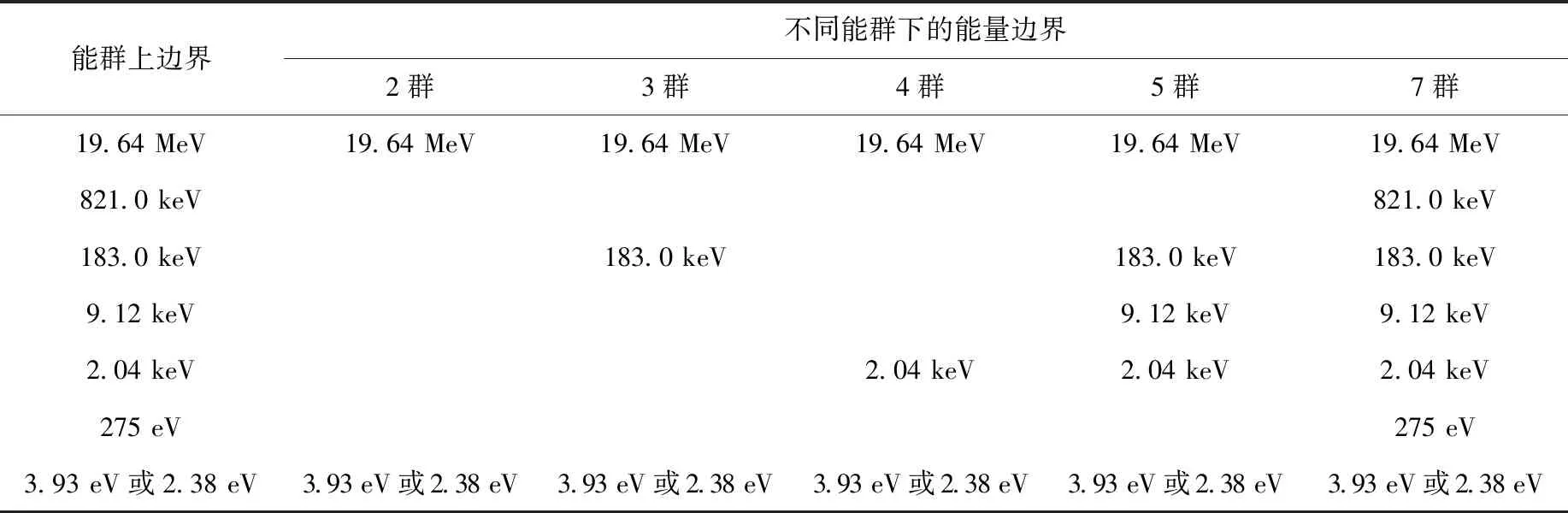
表2 5种少群常数能群结构Table 2 Five kinds of broad energy group structure

表3 能群结构划分的物理依据Table 3 Physical explanation for recommended group structure
2 计算结果
2.1 堆芯临界计算结果
基于少群能群结构计算了液态熔盐实验堆在运行温度为920 K时不同控制棒单独插入与组合插入堆芯时的有效增殖因数,计算结果如图7所示。
图7中,no rod表示控制棒全部拔出,rod 16表示调节棒rod 1和rod 6全部插入,rod 345表示补偿棒rod 3、rod 4、rod 5全部插入堆芯,all in表示堆芯内6根控制棒全插入堆芯。当快热能群分界为2.38 eV时,从2群到7群计算得到的最大相对误差依次为1.2%、0.9%、0.6%、0.5%、0.4%;当使用3.93 eV作为快热能群分界时,最大相对误差依次为1.3%、1.0%、0.7%、0.65%、0.48%。由此可知随能群数的增加计算精度也不断增加,当能群结构为7群时,计算精度可满足小于0.5%的要求。同时由图7可看出,2.38 eV快热能群分界具有更高的计算精度,因此采用2.38 eV作为快热能群分界。此外,最大计算误差均出现在调节棒rod 1与rod 6同时插入堆芯时的工况,其主要原因为控制棒组件均匀化时未考虑侧反射层石墨对能谱的影响,导致计算结果出现较大偏差。

图7 堆芯不同运行状态下的有效增殖因数(a)及与MCNP5结果的相对误差(b)Fig.7 Effective multiplication factor (a) and relative error compared with MCNP5 result (b) under different operating conditions of core
根据图7a不同控制棒插入堆芯的有效增殖因数,由下式计算控制棒插入堆芯后的积分价值:
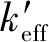
计算得到的控制棒价值如图8所示,由图8可看出,随能群数增加,控制棒价值也不断接近MCNP5的基准解,当能群数为7群时,最大绝对误差为274 pcm。
2.2 功率分布
为验证Dragon和Donjon程序对熔盐堆堆芯功率分布模拟的可靠性,使用7群结构,快热能群分界为2.38 eV,计算得到堆芯轴向与径向功率分布,并与MCNP5计算结果进行了比较。控制棒拔出与补偿棒组(rod 345)插入堆芯,两种条件下堆芯活性区轴向功率分布如图9所示。由图9可见:控制棒插入前后轴向功率分布基本没有变化,即轴向功率峰均在堆芯的中心;靠近上下熔盐腔室区域的功率与MCNP5程序计算结果有较大误差,最大相对误差为10%。出现误差的最主要原因是堆芯几何问题,即对堆芯进行等效建模时,将上下熔盐腔室等效为等体积燃料盐的长方体,从而引起堆芯轴向中子泄漏的增加,降低了此区域的功率。
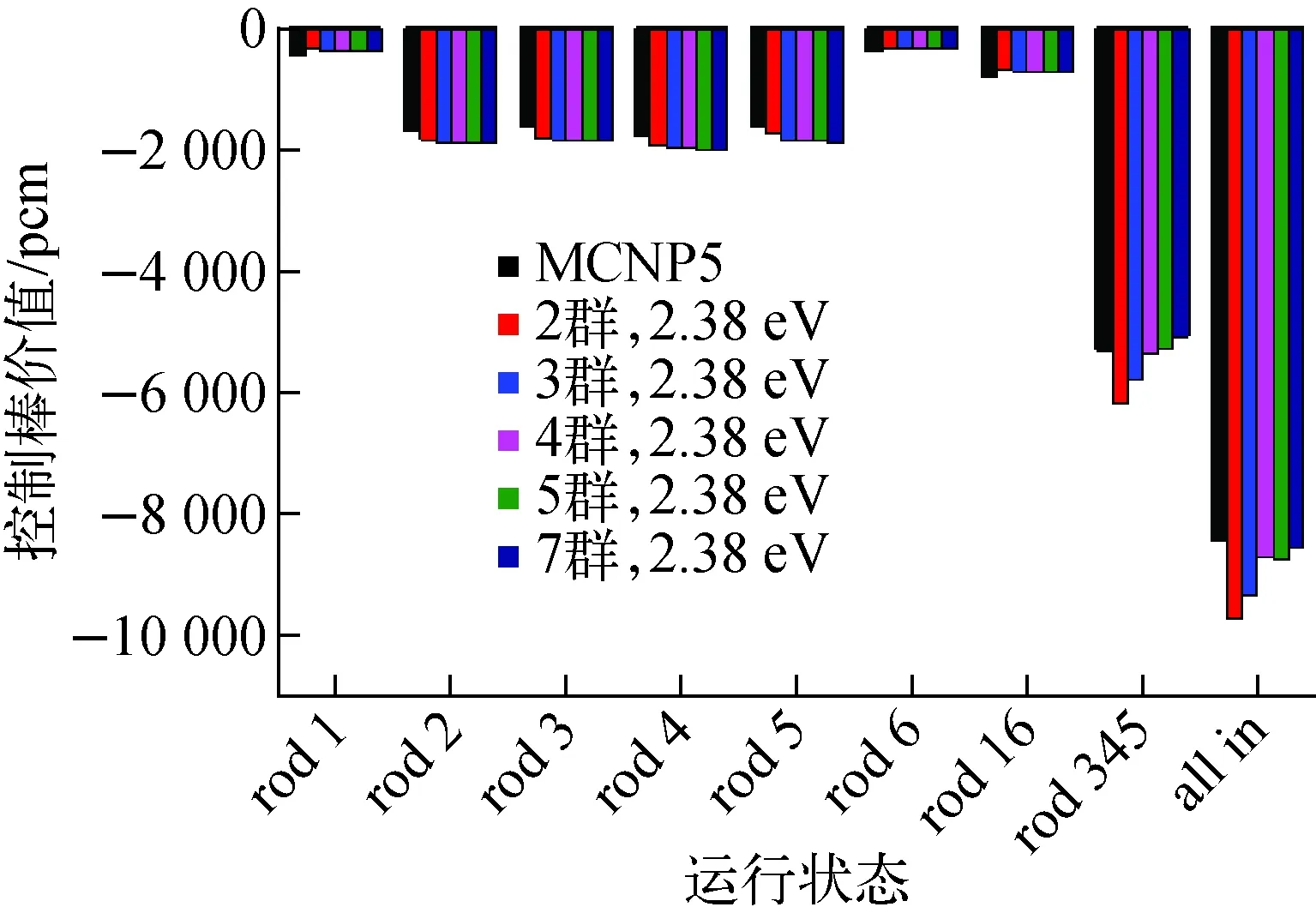
图8 单个控制棒与控制棒组的价值Fig.8 Control rod worth of single rod and rod group
由于确定论计算的全堆模型(图6)将径向反射层与燃料石墨组件边缘等效为不连续的矩形结构,因此MCNP5程序统计径向功率时不能与确定论网格完全对应。本文使用MCNP5程序统计功率时,使用了更小(边长为3 cm)的网格进行功率统计。图10对比了堆芯活性区轴向在80~90 cm处的径向功率分布。由图10可见:控制棒不插入堆芯前,功率峰因子在堆芯中心,且实验孔道与中子源孔道组件、控制棒孔道组件的功率均低于附近区域的功率;

图9 控制棒拔出(a)与补偿棒组插入(b)堆芯时的轴向功率分布Fig.9 Axial power distribution with control rod drawn out (a) and compensating rod inserted (b)
当补偿棒插入堆芯后,引起径向功率峰向2号控制棒孔道附近移动。从计算结果可知,MCNP5程序与确定论计算得到的径向功率分布基本相同。
a——无控制棒插入,MCNP5;b——无控制棒插入,确定论;c——补偿棒插入,MCNP5;d——补偿棒插入,确定论图10 堆芯径向功率分布对比Fig.10 Comparison of core radial power distribution
2.3 温度反应性系数
温度反应性系数是反应堆安全分析的重要参数,为保证反应堆具有本征安全性,总温度反应性系数必须为负。液态熔盐实验堆的总温度反应性系数可分解为燃料盐与慢化剂石墨的温度反应性系数,其中燃料盐的温度反应性系数由多普勒效应与密度效应组成,总的温度反应性系数计算公式[26-27]为:

由于液态熔盐实验堆燃料盐的运行温度范围为708~973 K,因此本文主要集中对700~1 000 K内的温度反应性系数进行计算分析。计算过程中,控制棒全部处于上限位。图11示出不同温度条件下采用7群结构计算所得到的堆芯有效增殖因数。由图11可看出,在不同温度条件下,计算所得到的堆芯整体、燃料盐、慢化剂的keff结果与MCNP5基准解的最大相对误差分别为0.17%、0.14%、0.20%。
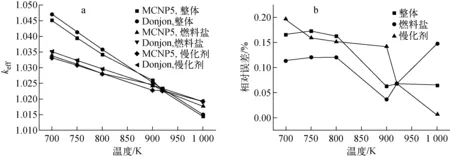
图11 不同温度条件下的有效增殖因数(a)及与MCNP5结果的相对误差(b)Fig.11 Effective multiplication factor (a) and relative error compared with MCNP5 result (b) at different temperatures
通过计算液态熔盐实验堆燃料盐与石墨分别在不同温度下的有效增殖因数,得到燃料盐、慢化剂和总的温度反应性系数,结果如图12所示。由图12可看出,实验堆总的温度反应性系数约为-10.5 pcm/K,燃料盐的温度反应性系数约为-5.1 pcm/K,慢化剂的温度反应性系数约为-4.9 pcm/K,与MCNP5计算结果的最大误差依次为0.58、0.12和0.58 pcm/K。
3 总结与展望
本文基于中子输运程序Dragon与中子扩散程序Donjon,使用传统的两步法对液态熔盐实验堆进行了临界分析,并通过MCNP5程序验证了Dragon与Donjon程序计算液态熔盐实验堆的适用性。本文使用5种少群能群结构进行了计算分析,并对快热能群分界进行了敏感性分析,结果表明使用7群少群结构计算得到的结果与MCNP5程序计算的基准解最为接近。
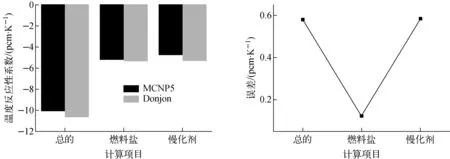
图12 温度反应性系数与MCNP5程序结果的比较Fig.12 Comparison of temperature reactivity coefficient with that calculated by MCNP5
本文主要围绕液态熔盐实验堆初始临界展开,暂未考虑燃耗计算以及燃料盐后处理,同时未考虑熔盐流动对计算结果的影响。下一步将耦合上述影响因素进一步拓展本工具在熔盐堆物理分析方面的模拟功能。
