基于弹性地基梁法的地下管线简化模型分析*

董国伟

(神华地质勘查有限责任公司，北京 100085)

0 引言

随着我国城市化进程的不断加快，城市地下空间的开发利用规模与日俱增，地下工程暗挖施工时经常会遇到近距离下穿既有地下管线分布情况，必然引起地下管线原有力学形态的改变，甚至引发管线泄漏破坏等事故，影响管线的正常运营和地下工程的施工安全[1]。因此，开展地下管线变形发展规律研究，成为当前地下空间开发利用中亟待解决的一项重要课题。

国内外尽管针对地下管线进行了大量的理论研究工作，但主要以有限元分析为主，不便于工程推广应用。目前地下管线的简化分析多按Winkler单参数地基梁法进行求解，如Takagi等[2]考虑管线与地层间存在相对位移，分析了隧道开挖过程中钢管、铸铁管的受力情况；Klar等[3]将Green函数引入地层连续位移，并与Winkler地基下无限长梁的最大弯矩计算值进行了对比；范德伟等[4]考虑地基扩散系数影响，分析了地铁隧道开挖过程中管棚的受力和变形机制；张桓等[5]针对隧道正交下穿管线情况，采用两阶段法建立了双参数地基模型的管线变形计算方法；姜峥[6]提出采用基坑开挖引起的土体附加变形作为弹性地基梁模型中的外部作用，分析了基坑一侧土体纵向变形适用的经验公式，给出了管线变形和内力的加权残值解；杨新强等[7]运用Elman网络法对管线的变形风险进行预测，研究了深基坑开挖引起的邻近管线的风险等级；魏纲等[8]基于统一土体移动模型解计算盾构隧道施工引起的土体自由位移场，通过能量方法建立变分控制方程，得到盾构隧道施工引起地下管线竖向位移的计算方法；之后，采用弹性力学Mindlin解推导出双线盾构在掘进过程中多因素引起的土体附加应力计算公式，并基于Winkler和Pasternak土体模型推导出单线和双线盾构施工中土体损失引起的垂直盾构方向管线竖向附加应力和位移计算公式[9-10]。然而，针对地下工程近距离平行下穿地下管线案例而言，为避免对上方既有管线产生破坏，在施工过程中经常需要对工作面前方影响区域内地层进行超前注浆加固[11-12]，此时，工作面前方地层模拟采用考虑水平剪切效应的Pasternak双参数弹性地基模型，既避免了Winkler单参数计算模型中地基不连续的不足，又避开了有限元法计算耗时上的缺陷。同时对下穿施工中的管线变形影响因素进行讨论，可为地下管线技术标准的完善提供理论参考。

1 地基与管线简化计算模型

1.1 基本假设

基本假设：①地下管线为等截面均质材料；②地基服从各向同性均匀介质假定；③管线结构与地基变形协调，在地下工程下穿施工支护段、未支护段、工作面前方段分别按支撑在Winkler弹性地基、简支梁及支撑在Pasternak双参数弹性地基上的梁计算；④管线结构上方作用荷载考虑按上覆土柱压力计算。

考虑管线为纵向传力结构，在笛卡儿坐标下，沿梁长(x方向)按下方支撑条件进行分段：支护段(AB)、未支护段(BC)、工作面前方扰动松弛段(CD)和前方未扰动段(DE)，如图1所示。

图1 分段管线简化模型示意图

1.2 Pasternak地基梁偏微分方程

在模型简化分析时，各梁段挠曲微分方程可分别表示如下

(1)

式中：p—覆土土柱压力，N/m2；w—弹性地基梁位移，m；b—地基梁宽度(采用圆管时取直径)，m；b*—地基梁等效作用宽度[13-14]，m；k—基床系数，N/m3；Gp—地基剪力传递系数，N/m2；EI—地基梁纵向抗弯刚度，N·m2。

对上述公式求解，可得

(2)

式中：c1～c16—由边界条件确定的待定参数；w*—与荷载和边界条件相关的特解；α、β、λ的表达式为

由材料力学知识，梁任一截面转角θ、弯矩M和剪力Q与挠曲变形w间满足关系式

(3)

基于各梁段间变形协调和受力平衡条件，梁始末端状态变量满足：

(4)

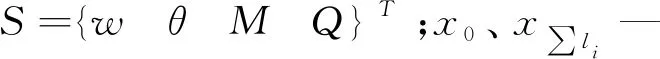
1.3 算例

取管径φ402 mm，壁厚t=16 mm圆形钢管计算模型，地下工程开挖净高为4.5 m、净宽4.2 m，施工长度为20 m，模拟开挖步距为0.5 m，各梁段基床系数分别取：k1=60×106N/m3、k2=0、k3=55×106N/m3、k4=75×106N/m3，剪力传递系数Gp=5.5×106N/m2，管段等效抗弯刚度1.0×108N·m2。上覆土柱压力按6 m深计算，土重度1 800 kg/m3。假定钢管在A端、E端(图1)满足如下边界条件

由Matlab编程计算由下发土体开挖引起的钢管纵向挠度变形曲线，当开挖长度取3 m时，计算结果，如图2所示。

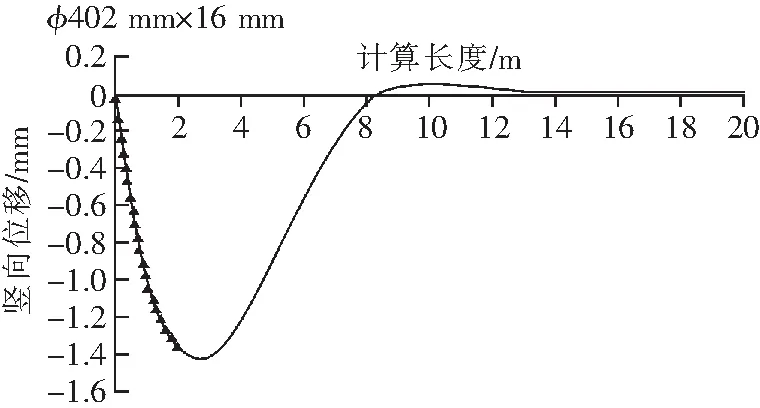
图2 梁纵向挠曲变形曲线

由图2中曲线变化规律分析可知：当管线下方开挖长度为3 m时，①沿钢管长度最大计算变形量为1.4 mm；②钢管最大变形发生在开挖工作面附近；③在距离工作面前方约1.5～2.0倍净空高度范围，受上方地层扰动松弛和工作面开挖卸荷共同影响，钢管产生约0.05 mm的隆起变形。由于变形量小，工程施工中可不予考虑其影响。

2 参数分析

为进一步研究管线下方开挖施工开挖步距、钢管截面尺寸2种因素对管线结构变形的影响关系，下面分别选取不同计算参数进行比较分析。

2.1 钢管管径影响

图3给出了模拟开挖步距为0.5 m时，钢管截面分别取φ402 mm×16 mm和φ1 200 mm×16 mm两种管径时的梁纵向挠曲变形曲线。

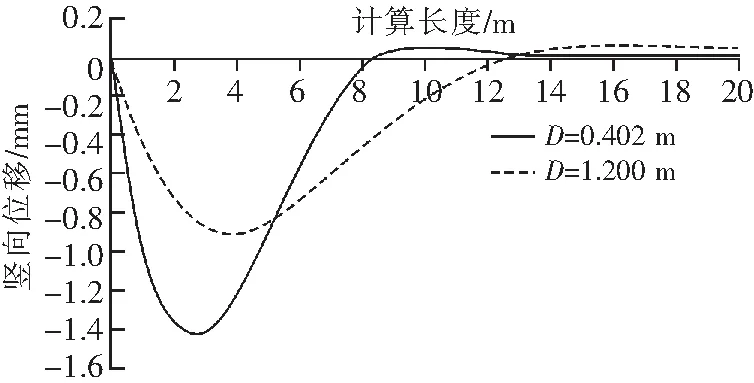
图3 梁纵向挠曲变形与管径关系

由图3分析可知，受钢管截面尺寸和抗弯刚度影响，管梁结构变形随管径增大而减小：其他条件不变，当钢管直径由402 mm增加至1 200 mm时，沿钢管长度最大计算变形由1.4 mm减小至0.9 mm，降低率为35%，说明选取不同的钢管直径与结构挠曲变形存在直接关系。

2.2 开挖步距的影响

分别取开挖步距为0.5 m、1.0 m和1.5 m 3种工况，图4给出了φ402 mm×16 mm钢管在不同开挖步距下梁的变形曲线。

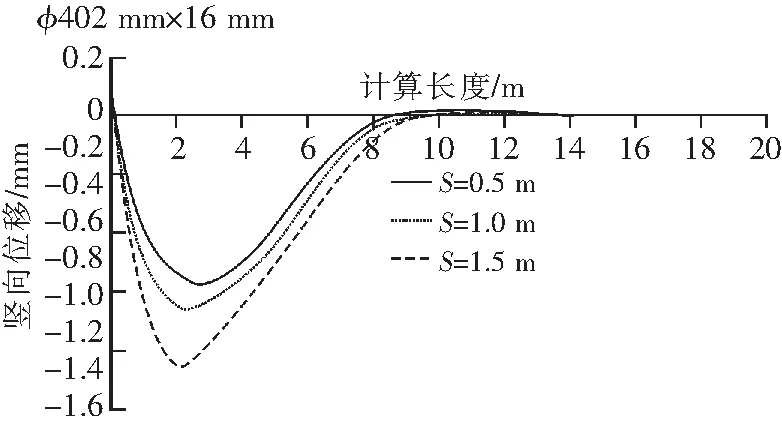
图4 梁纵向挠曲变形与开挖步距关系

由图4分析可知，管梁结构变形随开挖步距增加而增大：模拟开挖步距由0.5 m增至1.5 m，沿钢管长度最大计算变形由1.4 mm增加到2.2 mm，且近似呈线性增长关系，说明了控制开挖步距大小对控制钢管和上方地层沉降变形具有重要意义。

3 结论

(1)根据下方开挖支撑情况对地下管线进行计算分段，并假定为支撑在Pasternak弹性地基上的梁，建立各梁段力学模型及偏微分控制方程，并对沿管梁纵向受力和变形解析解进行了理论推导。

(2)以地下工程下穿施工引起管线结构变形为研究对象，并分别针对管线钢管截面尺寸和工作面开挖步距因素进行参数分析，得出：管线结构最大变形发生在下方土体开挖工作面附近，且在距离工作面前方约1.5～2.0倍净空高度范围，结构存在隆起变形；管线结构挠曲变形随管径的增大而减小、随管线下方开挖长度的增加而增大。

(3)与常用有限元分析方法相比，弹性地基梁法能够近似模拟地下工程下穿地下管线施工中的结构变形问题，快速提供结构变形发展规律，计算简便高效，是地下工程下穿地下管线施工中的一种简化分析方法。