一种新的连续面形变形镜的解耦控制方法

刘成 于飞 丁琳 宋莉 黄刚 郝中洋,2 李超 林喆,2



一种新的连续面形变形镜的解耦控制方法

刘成1于飞1丁琳1宋莉1黄刚1郝中洋1,2李超1林喆1,2

（1 北京空间机电研究所，北京 100094）（2 先进光学遥感技术北京市重点实验室，北京 100094）

文章针对空间遥感器镜面由于应力释放和温度变化等引入像差的问题，利用连续表面变形镜校正像差展开解耦控制技术研究。对于基于Zernike系数求解影响矩阵的传统方法的波前复原精度有限的情况，文章提出了一种新的直接波前影响矩阵的变形镜解耦方法，适用于点阵表达的波前面形和Zernike多项式表达的波前面形。经过仿真验证，该影响矩阵解耦方法比基于Zernike系数方法的解耦精度高、稳定性好。文章在新的直接波前影响矩阵的基础上，讨论了采样方式与驱动器分布对拟合面形的影响，论证了驱动器的三角分布比四角分布更适合拟合面形。同时通过仿真分析，得出当变形镜要实现的面形采样点数足够时，求解精度的提升效果有限的结论。这些研究成果可为连续表面变形镜对空间遥感器的像差校正提供相应的技术支持。

采样方式 采样点 驱动器分布 解耦控制 变形镜 空间遥感器

0 引言

随着对空间光学遥感器的分辨率水平和性能要求越来越高，高分辨率遥感器需要大口径、长焦距来保证遥感器的性能。在空间遥感应用中，光学系统受到应力释放、温度变化等影响导致有明显的像差[1]，最终这些像差会导致成像品质的降低，因此需要像差精密校正。1953年美国天文学家Babcock提出了用实时测量和实时校正来克服像差的设想[2]。此后，由于大型激光工程和光学系统对克服动态误差的需求迫切，而支撑技术日益成熟，自适应光学在20世纪70年代得到了迅速发展[3]。目前，自适应光学技术已经在地基天文观测、高能激光等多个领域获得成功应用[4]，也广泛应用于在轨光学误差检测和校正来保证成像系统的光学性能[5]。

变形镜驱动及控制技术是自适应光学领域的一项核心技术，变形镜是自适应光学系统的核心器件之一[6-7]。在外加电压的控制下，通过其镜面形变改变入射波前的相位，从而改善系统成像的品质[8-9]。根据入射畸变波前的相位信息，稳定、精确的求出校正电压是变形镜实现波前校正的关键。

目前多个参考文献[10-14]采用了基于Zernike多项式系数表达的影响矩阵，并据此求取驱动电压，这种表达方法不够精确，对求解电压的精度和稳定性有很大影响，同时在引入Zernike描述时，又会引入误差，基于此问题，根据空间遥感器的特点，目前连续变形镜的运用广泛[15-16]，参考文献[1，17-19]都是选择这种变形镜进行像差校正，探索其原因是连续表面变形镜具有响应速度快、波前拟合误差小、光能利用率高、空间分辨率高、能保持相位连续和易于抛光镀膜等优点[20]。因此，本文选择基于连续表面变形镜建模展开控制研究，引入了新的影响矩阵求解方法，提高了电压的求解精度和稳定性，为后期在空间遥感器中的像差校正提供参考。

1 变形镜的建模与影响矩阵

变形镜的主要性能指标包括面形影响函数和交联值，根据系统的要求变形镜的变形量一般为几个微米，位移分辨率为几个纳米，还有一个重要的指标是对不同空间频率波前像差的校正能力。该校正能力与变形镜的单位面积驱动器数量是密切相关的，如果需要进一步优化，同样的驱动器密度对不同结构的变形镜的校正能力是不同的，这就需要建立完整的模型，进行详细的分析。

1.1 影响函数与连续表面变形镜的建模

变形镜影响函数是建立在变形镜的两个重要规律之上的[21-24]：1）各个电极单独作用时变形量的线性叠加等于变形镜总的变形量；2）在单个电极作用下，变形镜的变形与电压的大小成正比。当仅有一个驱动电极加单位电压而其它电极仅由弹性力约束时，镜面的形变称为此电极的影响函数[25]。

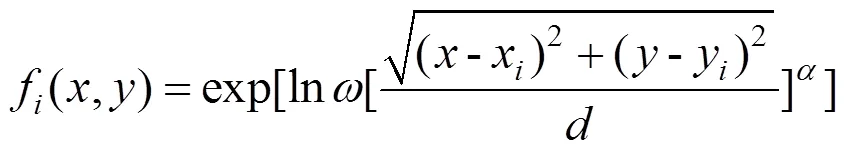
单个驱动器的影响函数是与高度正相关的，但仍存在相交变形。变形镜的整个面形由各个驱动器影响函数叠加所确定。那么对一个指定的面形，可以有表达式

一般变形镜的主孔径为圆形，每个驱动电极都是圆形结构。在建模过程中，对驱动器的大小忽略不计，通过文献资料的查询，驱动器的分布方式一般为四边形分布和三角分布（也可称为六边形分布）。本文选择三角分布，以直径为50mm、驱动器37个的OKO变形镜建模，取驱动器分布如图1所示。变形镜在37个驱动器驱动量都为单位量的情况下的图像如图2所示。

图1 变形镜驱动器的分布图

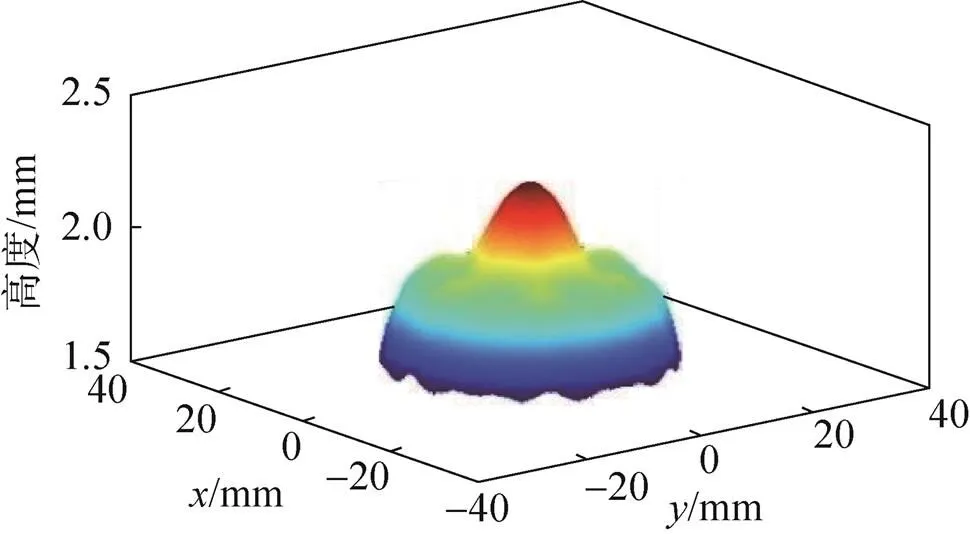
图2 单位驱动量下变形镜的立体图像

图2是全部驱动器驱动相同的位移形成的是类似圆锥体的立体图。这是因为交联值对每个驱动器的控制产生了耦合作用，控制产生需要的面形或者校正波前面形需要精确求解每个驱动器的驱动量，需要对算法进行研究。影响矩阵由此而来。

1.2 传统Zernike方法

Zernike多项式在20初世纪提出，之后经过完善用来描述波前像差。Zernike多项式可以用来明确地表示像差的物理意义，并在圆域内相互正交。公式为

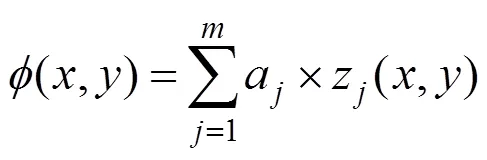
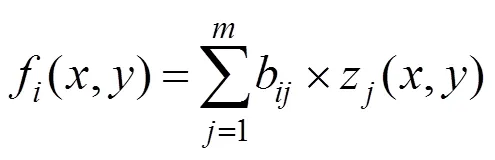
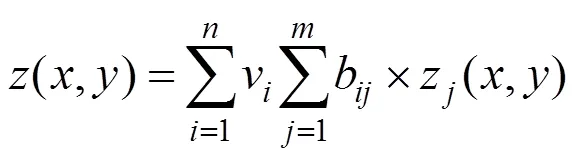
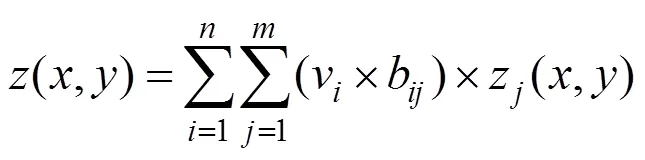
另一方面，传统Zernike方法是将各个驱动器的影响函数的Zernike系数向量保存在影响函数矩阵中，于是可以将式（6）改写为式（7）的形式，则得到变形镜与全部驱动器电压之间的关系

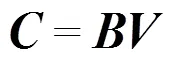
即

又因为变形镜是对波前的校正，根据校正的原理，有

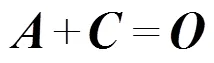
式中是波前像差Zernike系数组成的向量，表示和同维度的零向量。

所以，在已知波前的情况下，变形镜的驱动电压或者驱动量为

由于影响函数矩阵的在通常情况下是不可求解的，所以一般采取奇异值分解。

Zernike多项式仅适合表达缓变波前，驱动器影响函数具有在局部位置随空间快速变化的特征，很显然，Zernike多项式是不适合用于描述驱动器影响函数的，那么它在求解驱动量或驱动电压时的精度会受到限制。而且原始影响矩阵一旦确定之后，当作为输入的Zernike系数的项数存在变化时，方程就无法求解。若给的是一个点阵表达的波前面形，那么再用Zernike多项式表达，又会降低波前信息的准确性，对于求解的精度产生不良影响。所以，需要一种新的方法来进行解耦运算。

2 直接波前影响矩阵

针对Zernike系数对波前难以进行完全准确的表达，结合空间遥感器像差矫正时需要带宽较低而精度较高的特点，提出直接使用波前像差平面对变形镜的通道驱动量进行求取，即通过直接波前影响矩阵进行波前到驱动量的解耦。

在求解过程中，对于一个指定大小的面形，由式（1）和式（2）可以得到

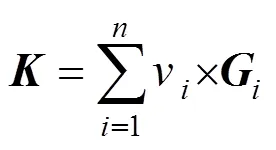
式中

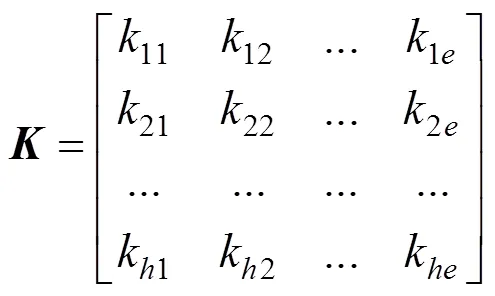
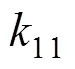
又因为每个波前曲面的面形可以用Zernike的表达式进行表达。对于指定区域内的面形，可以表达为

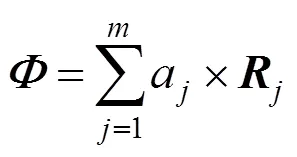
那么根据变形镜波前补偿原理有

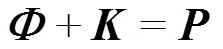
如果波前信息是一个面形，那么有

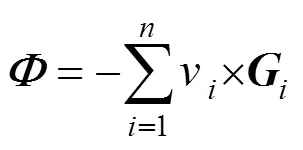
如果波前信息是用Zernike系数向量的形式给出的，那么有

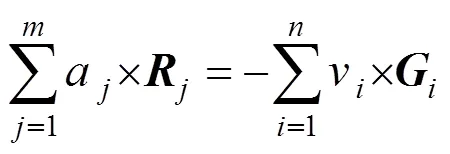
从式（14）看出，如果波前面形的信息用Zernike系数的形式给出，不管Zernike项数多少，同样可以算出需要面形的驱动量或者驱动电压。

因此，利用上述的直接波前影响矩阵方法，无论波前信息是直接给出波前面形还是Zernike系数向量表达式，都可以对其求解，而且可以不受Zernike项数的限制，也不受波前表达的局限。同时，该方法与传统Zernike方法求逆都是使用奇异值分解的方式。

3 仿真实验与结果分析

3.1 两种影响矩阵控制比较

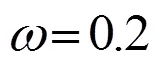
图3 两种影响矩阵的控制效果误差比较

表1 两种影响矩阵控制面形误差值的均值和方差

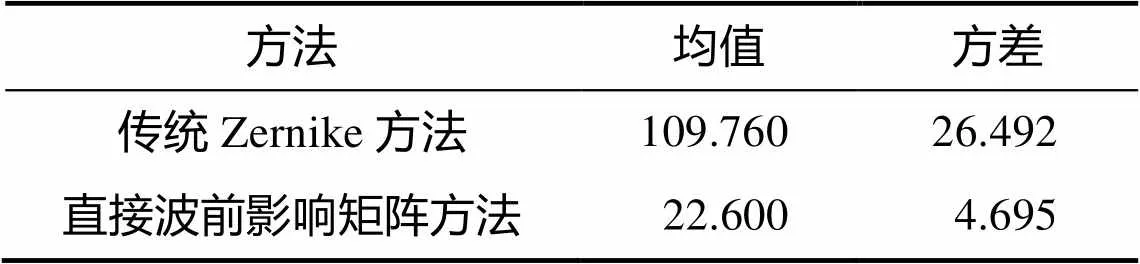
Tab.1 The mean and variance of the control error for two kinds influence matrices nm

从表1可见，传统Zernike方法的误差值的均值和方差比直接波前影响矩阵方法的误差的均值大5倍左右，说明直接波前影响矩阵方法的求解精度更高、稳定性更好。可见与通常采用的Zernike方法相比，本文提出的直接波前影响矩阵的面形解耦控制方法不但有更高的精度，而且解耦过程表现的更加稳定。

3.2 驱动器分布方式和波前采样方式的影响分析

（1）驱动器的分布影响

驱动器的分布方式一般为四角分布和三角分布（也可称为六边形分布）。但是，对于解耦控制而言，哪种分布方式更好，需要进一步验证。选择面形的大小相同，材料相同的变形镜，它们的交联值相同。四角分布选择驱动器44个，如图4所示，三角分布选择驱动器37个，如图5所示。

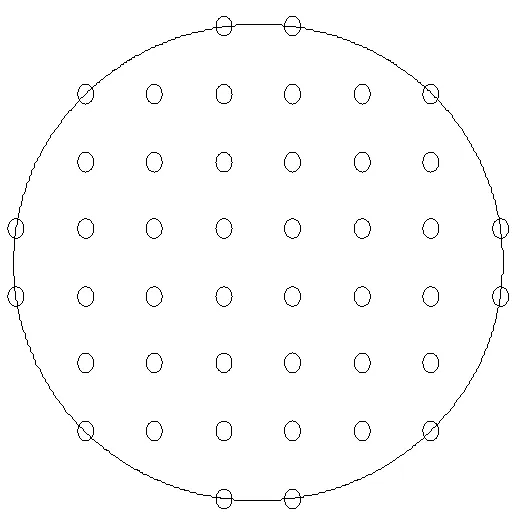
图4 驱动器四角分布示意图

图5 驱动器三角分布示意图

四角分布变形镜的面形大小为42mm，驱动器间的距离为5.92mm，中间是正方形分布，驱动器每行6个，每列6个，在正方形的每条边的旁边还有2个，一共44个驱动器。

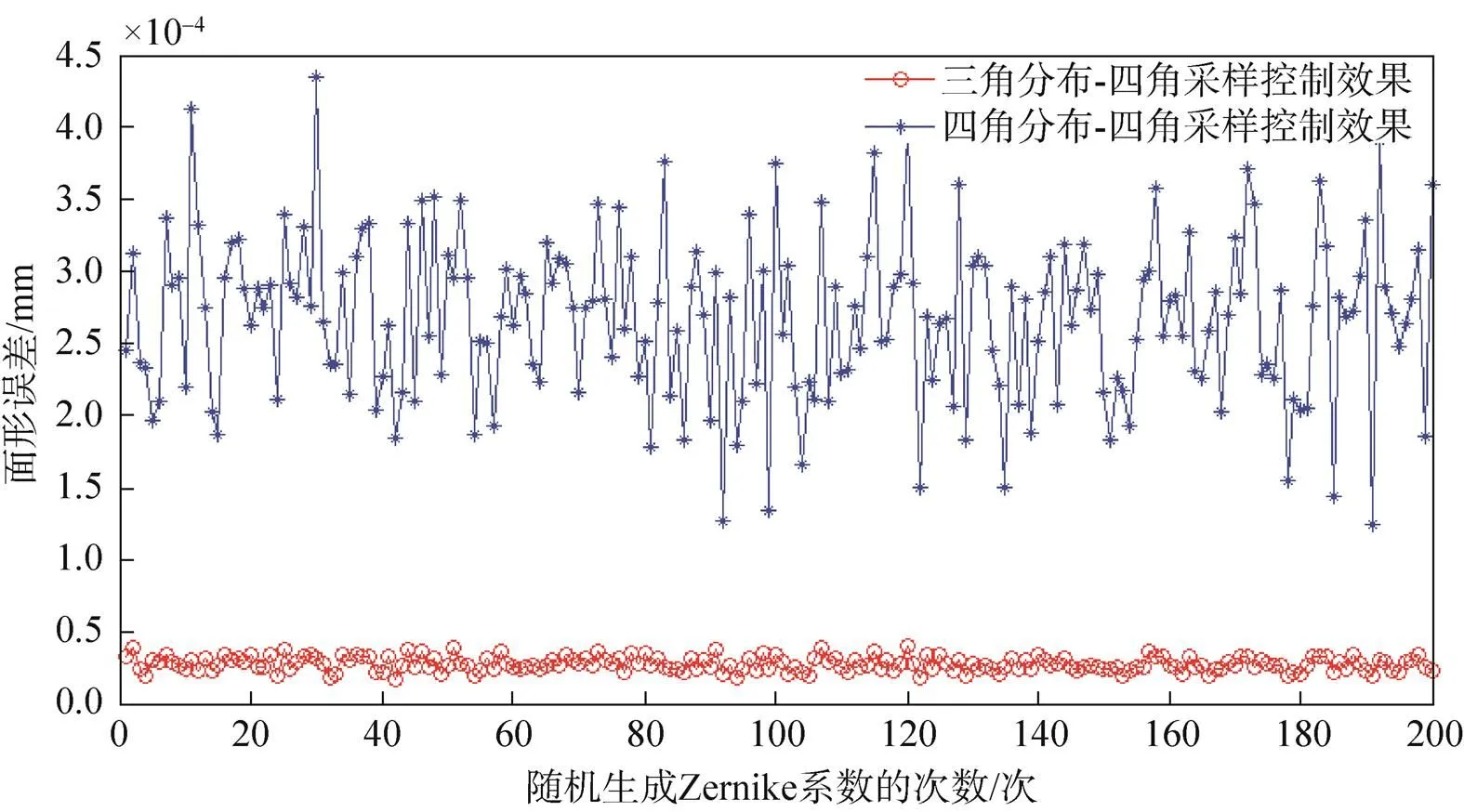
图6 四角采样方式下的两种驱动器分布方式控制效果误差值

三角分布变形镜的大小为42mm，驱动器之间的间距为7mm，驱动器一共37个，其中中间1个，第一圈6个，第二圈12个，第三圈18个，每一圈都是在圆环内均匀分布。

对应驱动器的四角分布和三角分布，波前面形的采样方式也对应的有四角方式和三角方式。因此需要结合驱动器的分布情况，对不同波前采样方式和驱动器分布方式进行分析。这里对前10项Zernike系数所表达的面形的控制精度进行分析，以原始面形和控制之后生成面形误差值作为评价指标。

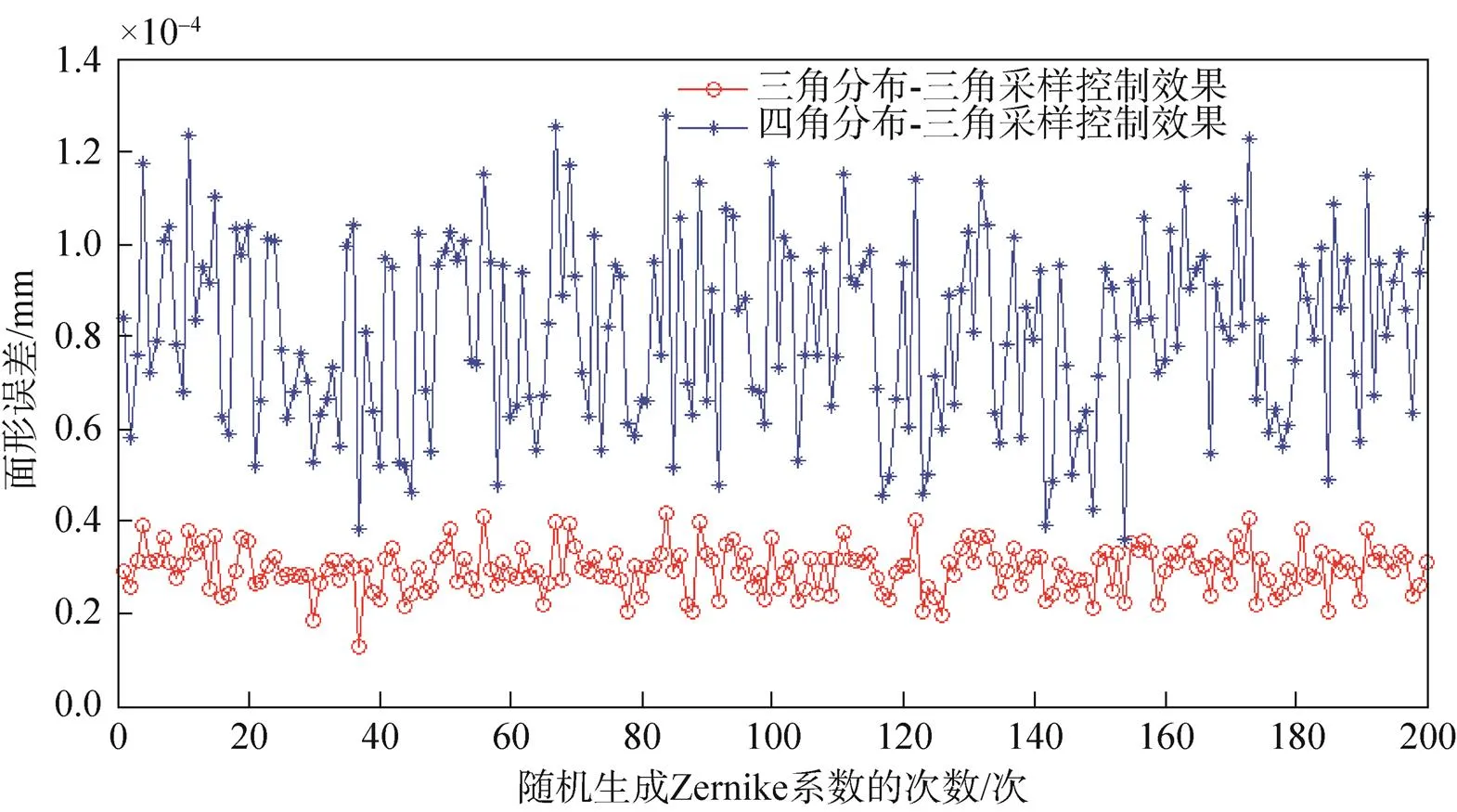
图7 三角采样方式下的两种驱动器分布方式控制效果误差值

表2 两种驱动器分布方式与两种采样方式下的面形误差的均值与方差

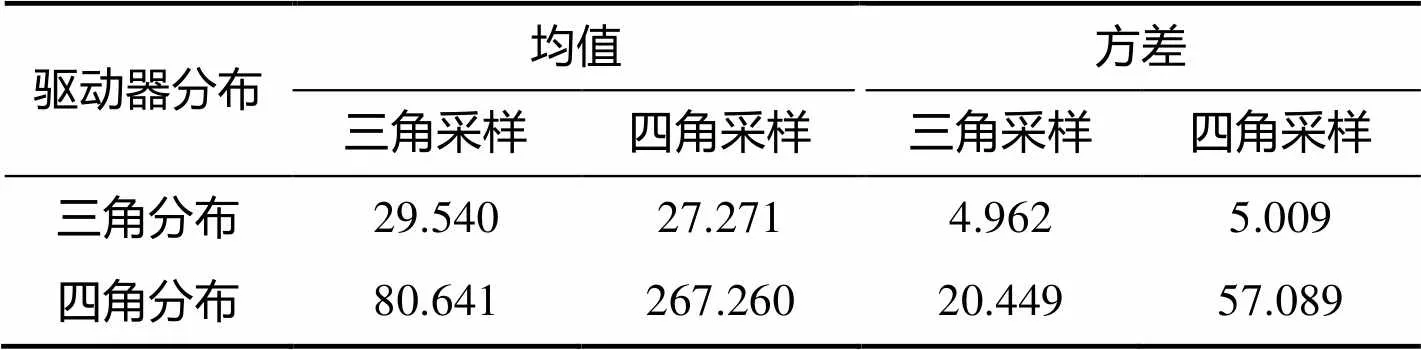
Tab.2 The mean and variance of error in two driver distribution modes and two sampling methods nm

根据图6、图7和表2可以看出，不管采样方式是三角采样还是四角采样，驱动器的三角分布相对于四角分布的情况，拟合面形的精度都要更高；在驱动器四角分布中，三角采样比四角采样对面形的拟合精度差；在驱动器三角分布中，四角采样的方式与三角采样的方式对面形的拟合精度差不多。

（2）波前采样点数影响

从式（10）的理论推导求解公式中可见，对于驱动量或驱动电压的精确求解主要是采样点的多少，因此需要对采样点数量需求进行评估。在求解驱动量或者驱动电压的过程中，采样点的点数至少要和驱动器的数目相等。为了评价采样点的多少对于驱动量的精确求解的客观性，首先用不同的采样点去求解驱动量或者驱动电压，然后再用相同的采样点去拟合相同的面形，通过原始面形与控制面形的误差值大小来评价求解的精确性。

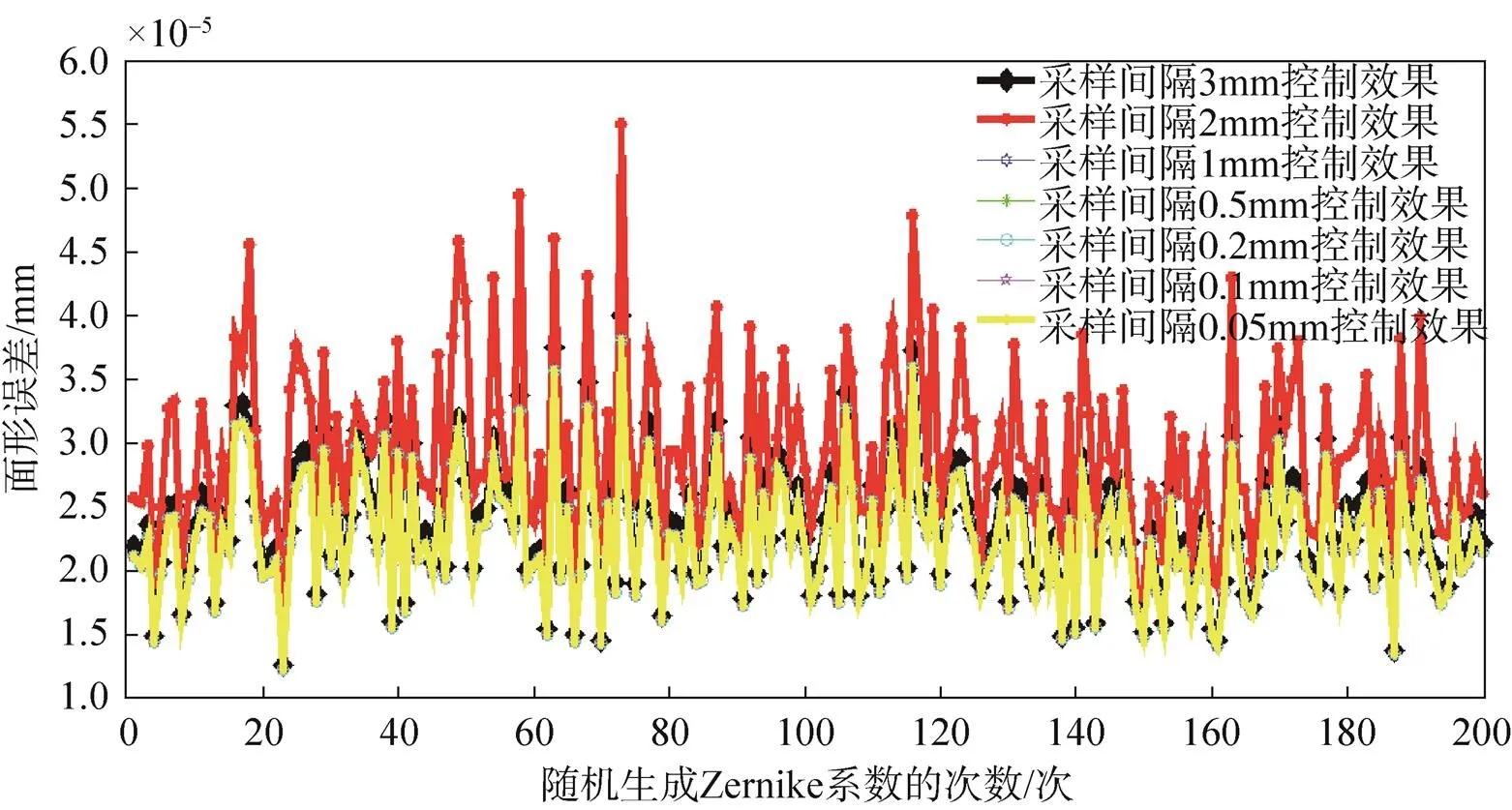
图8 不同采样间隔下的控制的误差值

表3 不同采样间隔的面形误差值的均值与方差

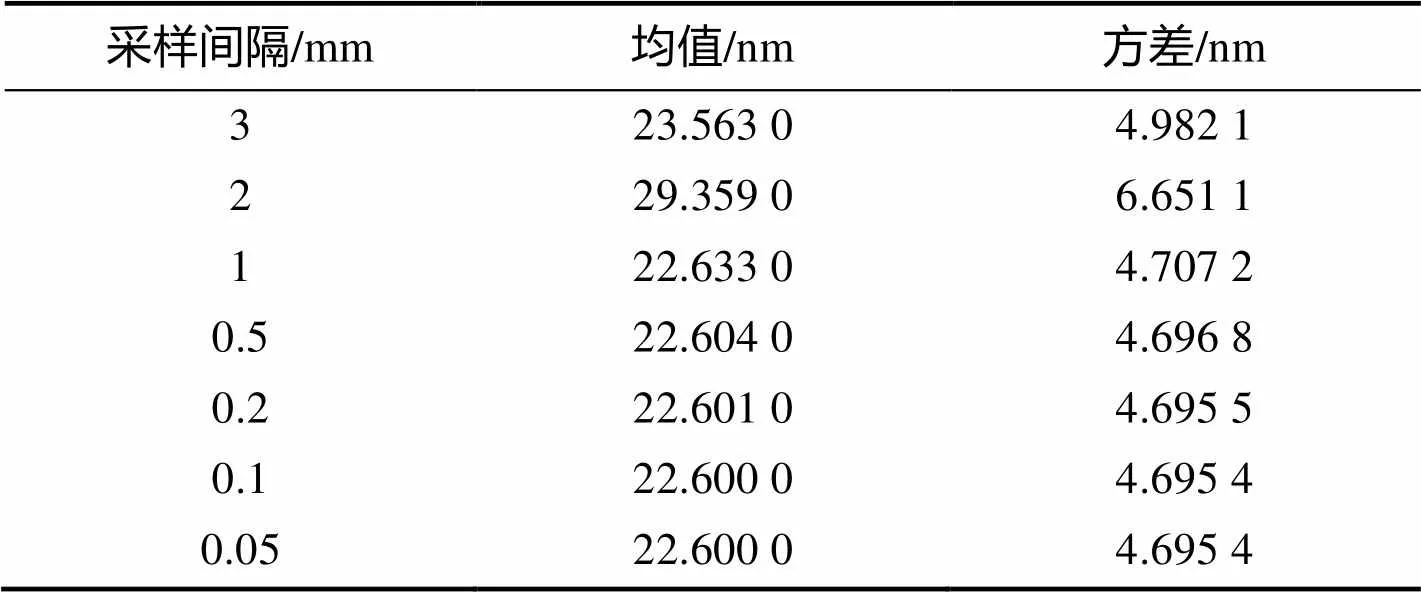
Tab.3 The mean and variance of surface figure error under different sampling intervals

从图8和表3看出，在采样间隔为3mm时的RMS误差值比采样间隔为2mm时的RMS误差值小，而其他线基本重合，说明采样点数少的情况下，求解的精度不是很稳定。然而，达到一定采样数量后，精度不会再提高，保持基本稳定。进而说明在求解驱动器的驱动向量时，采样点并不是越多越好，采样点达到一定数目之后，再多的采样点对于驱动量的求解精度作用有限。在实际应用中，需要根据实际面形的大小和驱动器数目的多少去选择合适的采样点。

4 结束语

本文对于基于Zernike系数求解影响矩阵的传统方法的波前复原精度有限的情况，提出了一种新的直接波前影响矩阵的变形镜解耦方法，适用于点阵表达的波前面形和Zernike多项式表达的波前面形。经过仿真验证，该影响矩阵解耦方法比基于Zernike系数方法的解耦精度高、稳定性好。在该方法的基础上，论证了驱动器的三角分布比四角分布更适合拟合面形。同时通过仿真验证得出当变形镜采样点数到达一定量后对解精度的提升效果有限的结论。这些研究成果可为连续表面变形镜对空间遥感器的像差校正提供相应的技术支持。

对于下一步的研究，将着重研究驱动器数量与采样点的定量关系，从而更好地对变形镜的控制提出技术指标。

[1] 凌宁. 自适应光学波前校正器[J]. 光学技术, 1998(3): 12-16. LING Ning. Adaptive Optical Wavefront Corrector[J]. Optical Technology, 1998(3): 12-16. (in Chinese)

[2] 周仁忠, 阎吉祥. 自适应光学理论[M]. 北京: 北京理工大学出版社, 1996. ZHOU Renzhong, YAN Jixiang. Adaptive Optics Theory[M]. Beijing: Beijing University of Technology Press, 1996. (in Chinese)

[3] 周仁忠. 自适应光学[M]. 北京: 国防工业出版, 1996:105-109. ZHOU Renzhong. Adaptive Optics[M]. Beijing: National Defense Industry Publication, 1996: 105-109. (in Chinese)

[4] Barchers J D. Closed-loop Stable Control of Two Deformable Mirrors for Compensation of Amplitude and Phase Fluctuations[J]. Journal of the Optical Society of America, 2002, 19(5): 926-945.

[5] 俞信, 张晓芳, 胡新奇. 空间自适应光学研究[J]. 航天返回与遥感, 2011, 32(5): 19-28. YU Xin, Zhang Xiaofang, HU Xinqi. Research on Space Adaptive Optics[J]. Space Recovery & Remote Sensing, 2011, 32(5): 19-28. (in Chinese)

[6] Hardy J W, Thompson L. Adaptive Optics for Astronomical Telescopes[J]. Physics Today, 2000, 53(4): 69.

[7] 姜文汉, 张雨东, 饶长辉, 等. 中国科学院光电技术研究所的自适应光学研究进展[J]. 光学学报, 2011, 31(9): 64-72.Jiang Wenhan, Zhang Yudong, RAO Changhui, et al. Research Progress of Adaptive Optics in Institute of Photoelectric Technology, Chinese Academy of Sciences[J]. Journal of Optics, 2011, 31(9): 64-72. (in Chinese)

[8] Fernandez E J, Vabre L, Hermann B, et al. Adaptive Optics with a Magnetic Deformable Mirror: Applications in the Human Eye[J]. Optics Express, 2006, 14(20): 8900.

[9] OWENS D, SCHOEN M, Bush K. MEMS Deformable Mirror Embedded Wavefront Sensing and Control System[J]. Proceedings of SPIE——MEMS/MOEMS Components and Their Applications Ⅲ, 2006, 6113: 249-260.

[10] 陈新荣, 李朝明, 王丹, 等. 小形变变形镜的设计及其在低像差脉冲压缩光栅中的应用[J]. 光学精密工程, 2016, 24(12): 2993-2999. CHEN Xinrong, LI Chaoming, WANG Dan, et al. Design of Small Deformable Mirror and Its Application in Low Aberration Pulse Compression Grating[J]. Optical Precision Engineering, 2016, 24(12): 2993-2999. (in Chinese)

[11] 李邦明, 沈建新, 廖文和, 等. 微机械薄膜变形镜校正性能及控制算法[J]. 强激光与粒子束, 2010, 22(7): 1558-1562. LI Bangming, SHEN Jianxin, LIAO Wenhe, et al. Correction Performance and Control Algorithm of Micromachined Thin Film Deformable Mirror[J]. Intensive Laser and Particle Beam, 2010, 22(7): 1558-1562. (in Chinese)

[12] 方迪. 基于微变形反射镜自适应光学系统原理与实验研究[D]. 武汉: 华中科技大学, 2005. FANG Di. Principle and Experimental Study of Adaptive Optics System Based on Micro Deformable Mirror[D]. Wuhan: Huazhong University of Science and Technology, 2005. (in Chinese)

[13] 杨平, 敖明武, 刘渊, 等. 基于泽尼克模式系数的自适应光学遗传算法[J]. 中国激光, 2008, 35(3): 367-372. YANG Ping, AO Mingwu, LIU Yuan, et al. Adaptive Optical Genetic Algorithms Based on Zernike Mode Coefficient[J]. China Laser, 2008, 35(3): 367-372. (in Chinese)

[14] 李恩德, 戴云, 王海英, 等. 微加工薄膜变形镜本征模分析[J]. 强激光与粒子束, 2006, 18(8): 1265-1270. LI Ende, DAI Yun, WANG Haiying, et al. Eigenmode Analysis of Micromachined Thin Film Deformable Mirrors[J]. Intensive Laser and Particle Beams, 2006, 18(8): 1265-1270. (in Chinese)

[15] Merritt P H. Beam Control for High-energy Laser Devices[J]. Optical Engineering, 2013, 52(2): 021005.

[16] Sinquin J C, Lurçon J M, Guillemard C. Deformable Mirror Technologies for Astronomy at CILAS[C]//SPIE Conference 7015: Adaptive Optics Systems. Marseille, 2008.

[17] Lowrey W H, Wynia J L, Ealey M A. Characterization of Three Advanced Deformable Mirrors[C]//SPIE International Symposium on Optical Science, Engineering, and Instrumentation. San Diego, CA: SPIE, 1998: 388-393.

[18] Jiang W H, Ling N, Li M Q, et al. Project of the 61-element Adaptive Optical System[J]. Pathologia Et Microbiologia, 1996, 23(1): 145-156.

[19] Lowrey W H, Wynia J L, Ealey M A. Characterization of Three Advanced Deformable Mirrors[J]. Proceedings of SPIE—The International Society for Optical Engineering, 1998, 3433: 388-393.

[20] 林旭东, 刘欣悦, 王建立, 等. 基于压电陶瓷促动器的连续镜面变形镜研制进展[J]. 激光与光电子学进展, 2014, 51(9): 27-36. LIN Xudong, LIU Xinyue, WANG Jianli, et al. Progress in the Development of Continuous Mirror Deformable Mirrors Based on Piezoelectric Ceramic Actuators[J]. Advances in Laser and Optoelectronics, 2014, 51(9): 27-36. (in Chinese)

[21] 李俊. 传输型详查相机微小自适应光学系统研究[D]. 武汉: 华中科技大学, 2006. LI Jun. Research on Micro-adaptive Optics System of Transmission Detailed Survey Camera[D]. Wuhan: Huazhong University of Science and Technology, 2006. (in Chinese)

[22] Gonte F, Courteville A. Optimization of Single-mode Fiber Coupling Efficiency with an Adaptive Membrane Mirror[J]. Optical Engineering, 2002, 41(5):1073-1076.

[23] Harvey J E, Callahan G M. Wavefront Error Compensation Capabilities of Multi-actuator Deformable Mirrors[C]// Proceeding of the Seminar Adaptive Optical Components. Washington D.C., 1978: 50-57.

[24] 林旭东, 薛陈, 刘欣悦, 等. 自适应光学波前校正器技术发展现状[J]. 中国光学, 2012, 5(4): 337-351. LIN Xudong, XUE Chen, LIU Xinyue, et al. Development Status of Adaptive Optical Wavefront Corrector Technology[J]. China Optics, 2012, 5(4): 337-351. (in Chinese)

[25] 饶学军, 凌宁, 姜文汉. 用数字干涉仪测量变形镜影响函数的实验研究[J]. 光学学报, 1995, 15(10): 1446-1451. RAO Xuejun, LING Ning, Jiang Wenhan. Experimental Study on Measuring the Influence Function of Deformable Mirror by Digital Interferometer[J]. Journal of Optics, 1995, 15(10): 1446-1451. (in Chinese)

[26] 尤俊成, 周虹, 官春林, 等. 913单元变形镜性能测试与分析[J]. 激光技术, 2017, 41(6): 867-871. YOU Juncheng, ZHOU Hong, GUAN Chunlin, et al. 913 Unit Deformable Mirror Performance Test and Analysis[J]. Laser Technology, 2017, 41(6): 867-871. (in Chinese)

[27] Huang L, Rao C, Jiang W. Modified Gaussian Influence Function of Deformable Mirror Actuators[J]. Optics Express, 2008, 16(1): 108-114.

[28] Allen J G, Brown J M, Christou J C, et al. Starfire Optical Range 3.5-m Telescope Adaptive Optical System[J]. Proc. SPIE, 1998, 3353: 22-33.

[29] 马剑强, 刘莹, 陈俊杰, 等. 200单元硅基单压电变形镜的设计与测试[J]. 光学精密工程, 2014, 22(8): 2047-2053. MA Jianqiang, LIU Ying, CHEN Junjie, et al. Design and Test of 200-unit Silicon-based Single Piezoelectric Deformable Mirror[J]. Optical Precision Engineering, 2014, 22(8): 2047-2053. (in Chinese)

[30] Vdovin G, Soloviev O, Loktev M, et al. Optimal Correction and Feedforward Control of Low-order Aberrations with Piezoelectric and Membrane Deformable Mirrors[J]. Proceedings of SPIE—The International Society for Optical Engineering, 2011, 8165(4): 185-224.

A New Decoupling Control Method for the Deformable Mirror with Continuous Surface Shape

LIU Cheng1YU Fei1DING Lin1SONG Li1HUANG Gang1HAO Zhongyang1,2LI Chao1LIN Zhe1,2

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China） （2 Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China）

In order to solve the problem of aberration caused by stress release and temperature change of mirror of space remote sensor, the decoupling control technology is studied using aberration correction of continuous surface deformation mirror. Due to the limited accuracy of the traditional Zernike coefficient-based wavefront restoration methods, a new deformable mirror decoupling method using direct wavefront influence matrix is proposed, which is suitable for wavefront expressed by both lattice and Zernike polynomial. The simulation results show that the influence matrix decoupling method has higher accuracy and better stability than those based on Zernike coefficient. Based on the new direct wavefront influence matrix, the influence of sampling mode and driver distribution on the fitting surface is discussed. It is proved that the triangular distribution of the driver is more suitable in fitting the surface than the quadrangular distribution. At the same time, the simulation analysis shows that when the number of surface sampling points on the deformable mirror is enough, the improvement effect of solution accuracy is limited. These results can provide technical support for aberration correction of space remote sensor by continuous surface deformable mirror.

Sampling Modes; Sampling Points; Driver Distribution; Decoupling Control; Deformable Mirror; Space Remote Sensor

TP273.2

A

1009-8518(2019)02-0089-10

10.3969/j.issn.1009-8518.2019.02.010

刘成，男，1993年生，2016年获西安电子科技大学学士学位，现在中国空间技术研究院精密光电仪器控制专业攻读硕士学位。研究方向为基于连续变形镜的多变量解耦控制。E-mail：liucheng520zf@163.com。

2018-08-29

国家重大科技专项工程

（编辑：庞冰）