贵州省数值预报风速产品检验及订正

夏晓玲,尚媛媛,郑 奕

(贵州省气象服务中心,贵州 贵阳 550002)

0 引言

风能，具有可再生性，是一种清洁能源，且储量巨大,是当今世界上可再生能源开发技术最成熟的发电技术，且在减轻污染等方面展现了良好的发展前景，在可再生能源中最适合大规模开发利用[1-3]。风电能占整个电网比例的大小取决于很多因素，最重要的是风速的预测[4]。由于大气边界层中的风场具有间歇性和不确定性[5-6]，因此现有的中尺度数值模式模拟风场[7-9]，特别是近地层风场具有较大误差。风速的瞬时性、脉动性以及对地形的依赖和敏感性，模式的风速模拟结果具有很大的不确定性[10-11]。目前风电场风速模拟预测的误差在25%～40%之间[12-13]。贵州省多山地地形，风能资料的利用难度和平原省份相比较大[14]，而风速预报的准确性是风功率预测的基础，对风电场的运行效率产生直接的影响。将数值预报的风速产品进行检验是研究风速预报的一种普遍的方法。关于数值预报对于风速预报的检验，国内已有很多研究成果[15-19]。对数值预报产品的误差进行订正的常用方法包括数据产品解释应用MOS方法、神经网络、支持向量机[20]、非线性回归、最小偏二乘估计[21]、Kalman滤波等，其中应用最为广泛的是MOS方法[22-23]和Kalman滤波。梁志文检验了T639模式和利用BP神经网络方法对T639模式订正后的集宁站的风速预报效果，结果表明，经人工神经网络订正后，风速预报比T639模式预报有明显的改善[24]，张颖超等运用了ELM算法对WRF模式预报风速进行订正，并发现相比其他智能算法(BP神经网络，SVM算法)，ELM算法对WRF模式预报风速具有较好的订正效果[25]，石岚等研究了多模式风速融合的预报应用，并认为融合现有数值预报产品，对改善单一数值预报性能具有明显效果，但是对风速的转折波动预测还存在一定不足之处[26]，丁圣等检验了基于WRF的模式的元江羊岔街风电场功率短期预报效果，发现进行离群值修正后的预报结果满足超短期(4 h)和短期预测月均方根误差要求，可以投入业务运行[27]。

目前针对贵州省范围内的数值预报风速效果的研究较少，本文检验了ECWMF(以下简称EC)、GRAPES和JAPAN对贵州省84个站点的10 m风速预报效果，考察3种模式风速预报的平均绝对误差、标准差、相关系数和正确率，并运用BP神经网络方式对两种模式风速预报进行订正，检验订正效果。

1 数据与方法

1.1 数据

本文检验了EC、GRAPES模式和Japan 3种模式预报时效为48 h的风速预报情况，3种模式的时间分辨率均为逐3 h，其中EC模式数据自2017年10月1日—2018年4月10日共192 d，剔除实况和预报缺值、空白和异常数据后，有效样本数为95.37%；GRAPES模式数据自2017年4月20日—2018年5月31日共407 d，有效样本数为98.25%；Japan模式数据自2017年4月20日—2018年5月31日共407 d，有效样本数为75.98%。

1.2 方法

1.2.1 误差检验 平均绝对误差可以用来反映预报值与实况值之间的偏离程度，可以反映总误差情况，是用来衡量预报误差比较常用的一个统计参数。平均绝对误差公式如下：其中xf为实况值，xo为预报值。

标准差反映了检验区域内误差幅度的平均状况，对误差的极值反映较为敏感，可以反映误差的离散程度，标准差公式如下：

1.2.2 趋势检验 检验数值模式对风速趋势的预报效果，本文采用相关系数来检验，相关系数是用来反映预报值与实况值的线性相关程度，相关系数的绝对值越接近1，说明模式对风速的变化趋势有一定的预报能力。相关系数的公式如下：

1.2.3 准确率检验 分别定义误差小于0.5 m/s、1 m/s、2 m/s时为预报准确,统计预报准确率,查看模式对风速的预报效果。

1.2.4 订正方法 本文检验数值预报对风速的预报效果，首先定义误差为实况值减预报值，分站点，分区域检验实况与预报的相关系数，误差的标准差、平均绝对误差，并分别检验误差小于0.5 m/s、1 m/s、2 m/s时的准确率。订正数值预报首先随机选取一部分数据，运用一元线性回归方式和BP神经网络建立订正模型，然后运用其余数据，带入订正模型，检验订正后的相关系数、标准差、平均绝对误差和准确率。

2 模式风速预报效果检验

2.1 EC模式检验

EC模式对于贵州气象站点风速预报的平均误差在-1.9～1.7 m/s之间(图略)，其中73.8%的站点平均误差小于0，故EC模式对贵州省风速的预报较实况偏大。全省站点平均绝对误差在0.6～2.1 m/s之间(图1c)，可以看出省的北部地区平均绝对误差较中部和南部明显偏小，中部次之，西部平均绝对误差最大，其中省的西部乌蒙山附近的威宁、毕节、织金、纳雍；苗岭附近的晴隆，长顺，为偏差高值中心，平均绝对误差均大于1.5 m/s。标准差分布情况和平均绝对误差相似，北部地区最低，中部次之，西部最高，全省站点标准差在0.8～2.5 m/s之间(图1a)。

从相关系数分布(图1b)可以看出，全省站点相关系数平均数为0.5，相关系数较低的几个站点均在省的东部地区，分别位于武陵山脉附近的沿河、松桃、思南；以及省东部的台江和锦屏。可以看出误差分布和相关系数的分布并不相似，预报误差较大的站点，趋势预报效果不一定较差。

风速预报误差绝对值为2 m/s的准确率全省平均值为83%，站点准确率分布图(图1d)可以看出，其分布规律与平均绝对误差相似。北部地区准确率最高，基本在80%以上；准确率低于70%的几个站点都在省的西部地区，其中织金的准确率最低为54%。

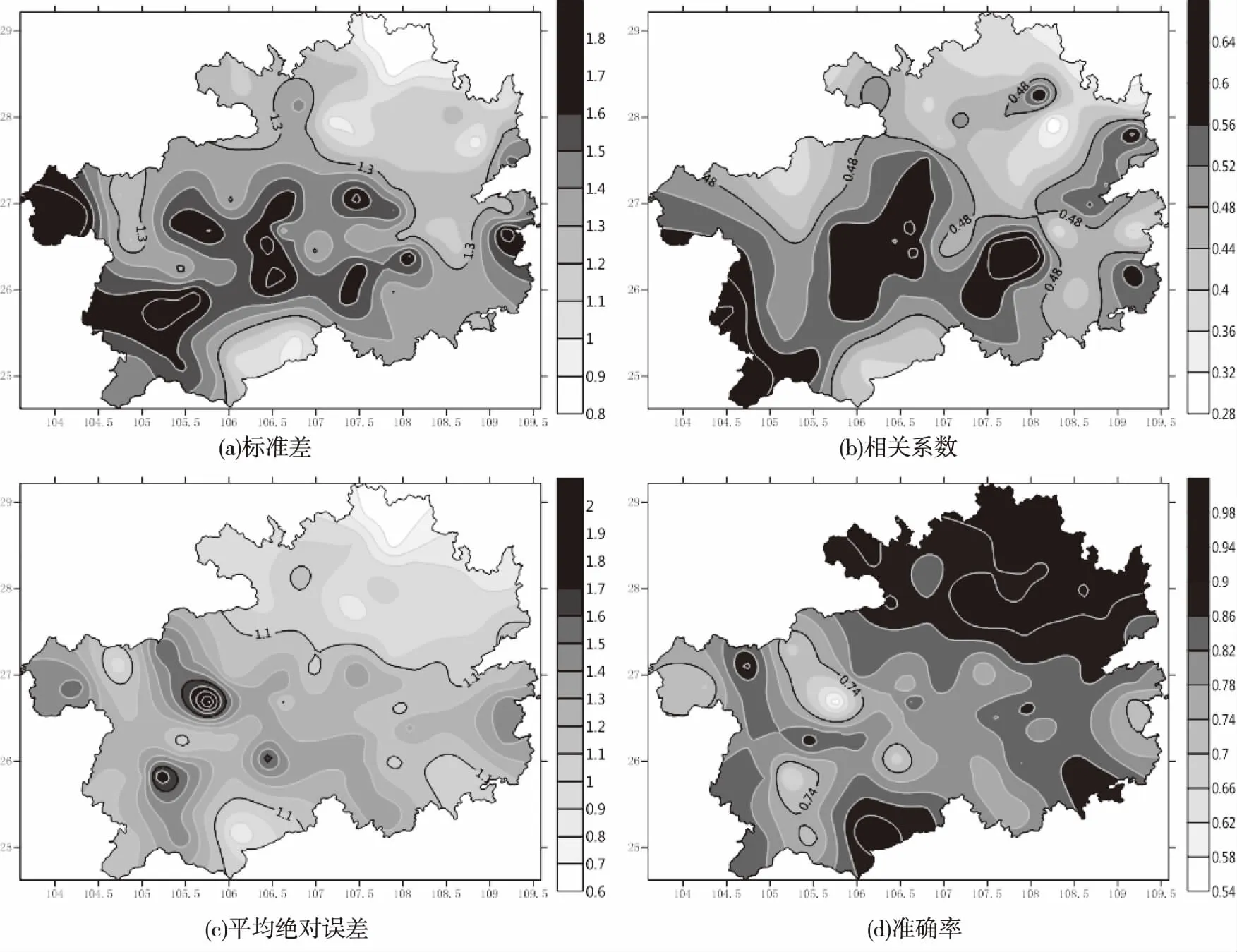
图1 EC模式在贵州风速预报效果图Fig.1 Wind speed forecasting effect of EC mode in Guizhou

2.2 GRAPES模式检验

GRAPES模式对于贵州气象站点风速预报的平均误差在-3.1～0 m/s之间(图略)，所有站点平均误差小于0，GRAPES模式对贵州省风速的预报较实况明显偏大，应该存在系统误差。全省站点平均绝对误差在1.1～3.3 m/s之间(图2c)，可以看出省的东部和西南部部分地区平均绝对误差较西北部和北部部分地区明显偏小，中部次之，西北部平均绝对误差最大，其中省的西部乌蒙山附近的威宁、六盘水、织金、纳雍；苗岭附近的长顺，为偏差高值中心，平均绝对误差均大于2.8 m/s。标准差分布情况和平均绝对误差相似，东部和西南部边缘最低，北部次之，西部最高，全省站点标准差在1.1～3.3 m/s之间(图2a)。

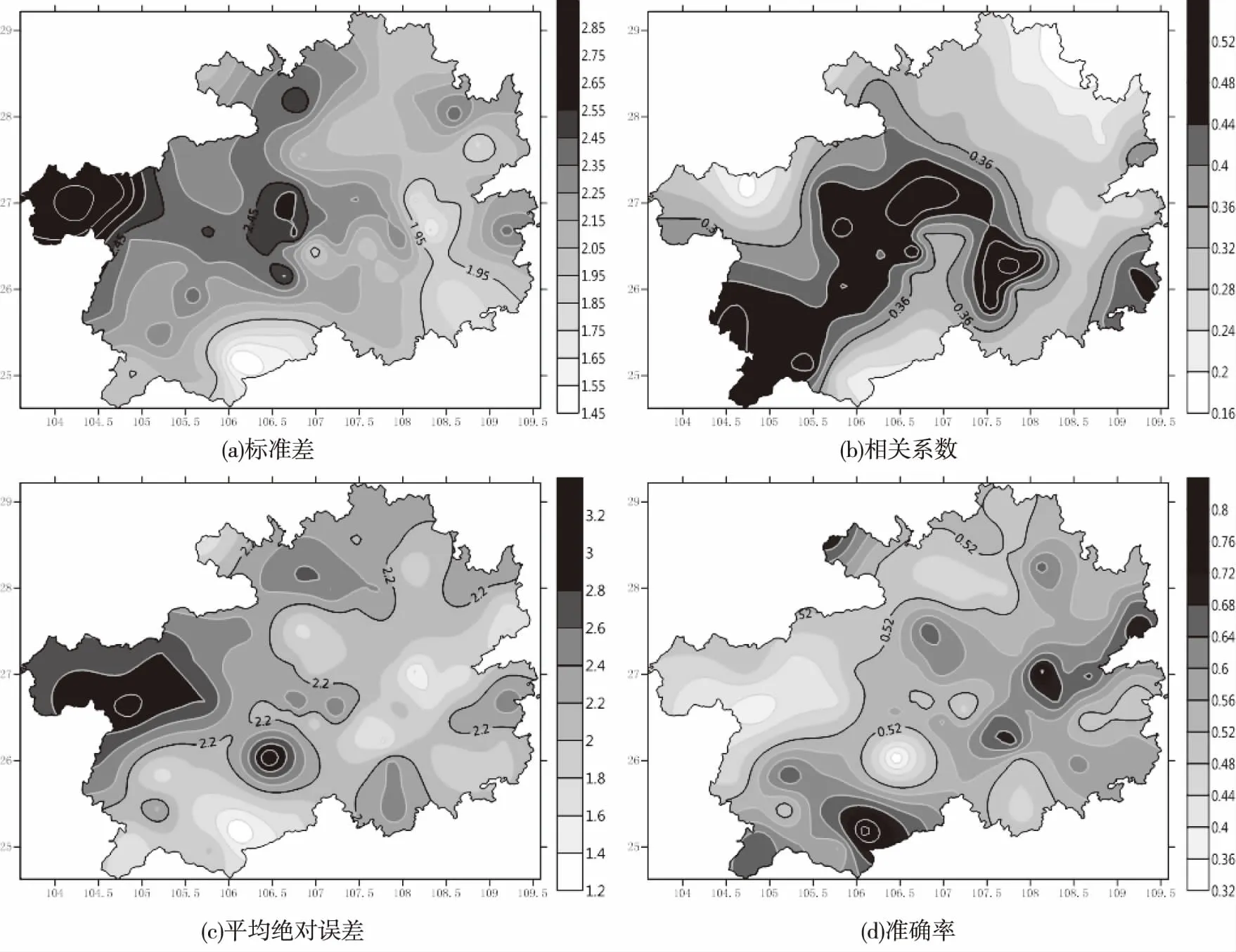
图2 GRAPES模式在贵州风速预报效果图Fig.2 Wind speed forecasting effect of GRAPES mode in Guizhou

从相关系数分布(图2b)可以看出，全省站点相关系数平均数为0.4，相关系数较低的几个站点均在省边缘地区，分别为省东北部边缘的沿河、务川，西南部边缘的册亨和西北部边缘的赫章。与EC相似的可以看出误差分布和相关系数的分布并不相似，预报误差较大的站点，趋势预报效果不一定较差。

风速预报误差绝对值为2 m/s的准确率全省平均值为56%，站点准确率分布图(图2d)可以看出，其分布规律与平均绝对误差相反。东部部地区准确率最高，基本在60%以上；准确率低于40%的两个站点都在省的中西部地区，其中长顺的准确率最低为32%。

2.3 JAPAN模式检验

JANPA模式对于贵州气象站点风速预报的平均误差在-3～1.9 m/s之间(图略)，54%的站点平均误差小于0，JAPAN模式对贵州省风速的预报较实况偏大。全省站点平均绝对误差在0.6～3.1 m/s之间(图3c)，可以看出全省大部分地区平均绝对误差小于1.7 m/s，省的中部部分地区和西部边缘平均绝对误差最大，其中省西部的赫章；苗岭附近的长顺、龙里，为偏差高值中心，平均绝对误差均大于2.5 m/s。标准差分布情况和平均绝对误差相似，东部和西南部边缘最低，北部次之，西部和中部最高，全省站点标准差在0.8～2.2 m/s之间(图3a)。

从相关系数分布(图3b)可以看出，全省站点相关系数平均数为0.5，相关系数较低的几个站点均在省边缘地区，其中省的东北部边缘的沿河、和西北部边缘的赫章相关系数小于0.2。

风速预报误差绝对值为2 m/s的准确率全省平均值为75%，从站点准确率分布图(图3d)可以看出，其分布规律与平均绝对误差相反。全省82%的站点准确率在60%以上；准确率低于30%的两个站点都在省的中部地区，其中长顺的准确率最低为29%。

2.4 3种模式预报效果对比

针对贵州9个地州市对比分析3个模式风速预报效果(表1)，可以看出24 h预报时效内EC模式的预报效果明显优于其他两个模式，标准差和平均绝对误差基本低于其他两个模式，相关系数和准确率也高于其他两个模式。将同一模式的4个检验指数相加，用于综合评价模式对该地区的预报效果，由于标准差和平均绝对误差是越小越好，故相加的为其相反数，相加的数值越大，证明预报效果越好(表略)。其中，EC模式对铜仁地区的预报效果最好，黔西南的预报效果最差，GRAPES模式对遵义地区的预报效果最好，毕节地区的预报效果最差；JAPAN模式对遵义地区的预报效果最好，黔西南地区的预报效果最差。3个模式中有两个在黔西南地区的预报效果不佳。

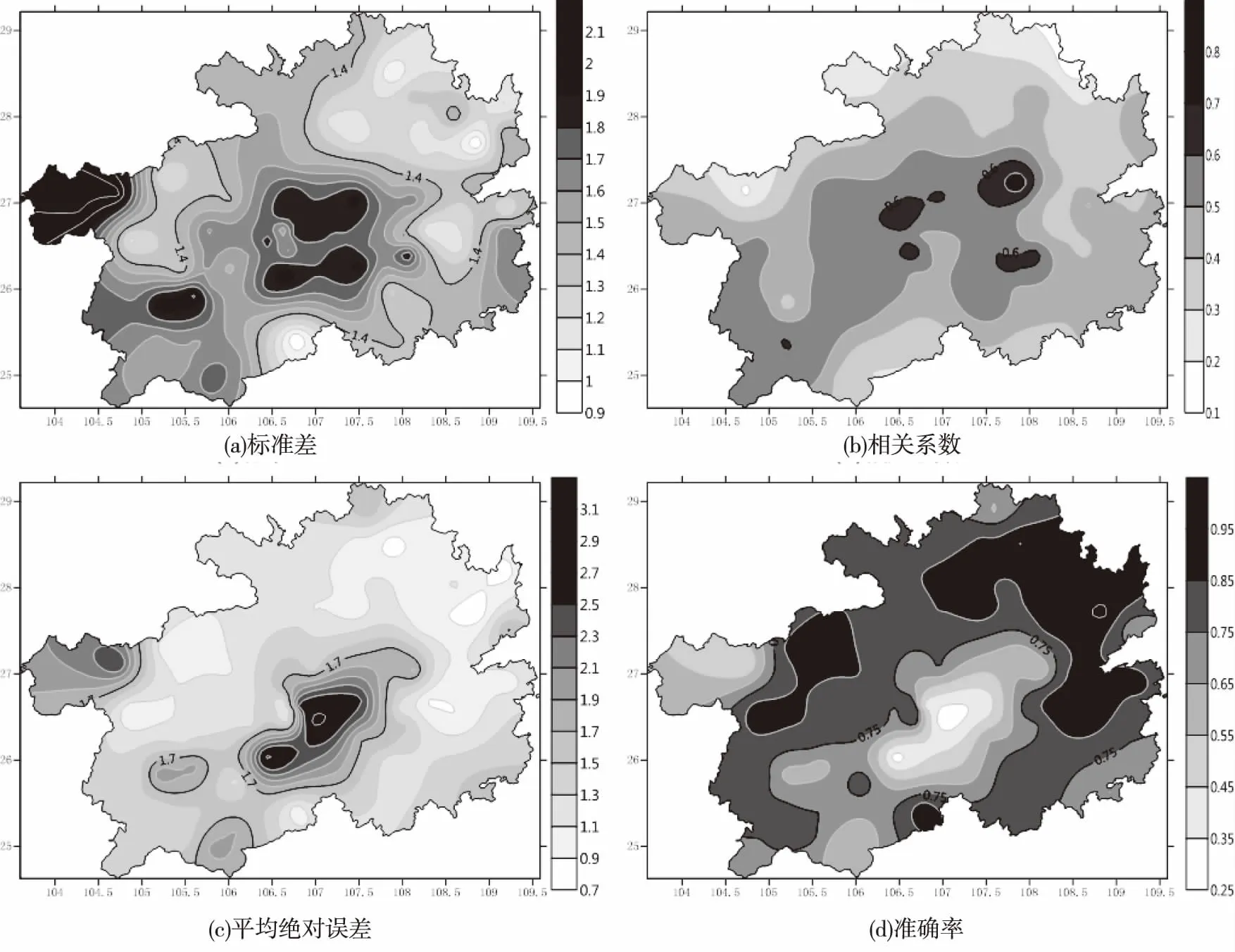
图3 JANPA模式在贵州风速预报效果图Fig.3 Wind speed forecasting effect of JANPA mode in Guizhou

表1 3种模式对9个地州市预报效果检验
Tab.1Testingtheforecasteffectofthreemodelsinninecities

标准差/(m/s)ECGEAPESJAPAN相关系数ECGEAPESJAPAN平均绝对误差/(m/s)ECGEAPESJAPAN准确率/%ECGEAPESJAPAN安顺1.572.161.710.570.480.501.201.881.430.820.620.75毕节1.572.371.830.490.400.371.392.331.370.760.530.77黔南1.532.141.850.570.440.551.292.021.950.790.580.58贵阳1.582.291.990.580.500.471.211.921.510.820.610.73黔东南1.401.921.670.550.410.451.171.711.320.830.660.78六盘水1.462.221.490.510.410.461.112.281.150.860.520.84铜仁1.231.951.380.520.310.330.951.741.050.900.660.87黔西南1.712.002.070.470.460.181.291.631.600.790.690.70遵义1.212.051.550.460.340.820.931.931.180.900.610.83

3 模式订正及效果检验

运用MATLAB神经网络工具箱，选取3种模式中80%的数据用于建立预报和实况的订正模型，剩余20%数据用于检验订正模型效果，由于神经网络隐藏层数和隐藏层节点数对模型的准确性有一定的影响，故本文建立的隐藏层数为1～2层，每层神经网络节点数为1～10个，共110个神经网络结构，并检验订正后数据和实况之间的相关系数，误差的标准差、平均绝对误差、误差小于2 m/s时的准确率。

3.1 EC模式订正及效果检验

EC模式检验中，随机选取了418 155个样本进行训练和建立神经网络模型，运用剩余104 539个样本进行检验。可以看出，运用BP神经网络对风速进行订正后，5个检验数据都有明显的提高。订正后的平均误差的范围在-0.012～0.001 m/s之间，相比未订正过的-0.282 m/s有明显的提高，且平均绝对误差相比未订正的下降0.09 m/s左右，误差的标准差下降0.08 m/s左右，说明神经网络订正方法降低的EC模式预报误差的离散程度，对误差的极值有一定的订正效果。订正后的正确率提高0.04左右，相关系数改善较小，说明BP神经网络对模式预报的风速趋势变化影响不大。

表2 EC模式BP神经网络检验结果Tab.2 EC model BP-Neural network test results

3.2 GRAPES模式订正及效果检验

GRAPES模式检验中，随机选取了913 682个样本进行训练和建立神经网络模型，运用剩余228 421个样本进行检验。可以看出，运用BP神经网络对风速进行订正后，5个检验数据都有明显的提高。订正后的平均误差的范围在-0.003～0.009 m/s之间，相比未订正过的-1.6 m/s有明显的提高，平均绝对误差相比未订正的下降0.9 m/s左右，误差的标准差下降0.6 m/s左右，同EC模式相比，对离散程度的改进效果明显。订正后的正确率提高0.2 m/s左右，相关系数改善较小，说明BP神经网络对模式预报的风速趋势变化影响不大。

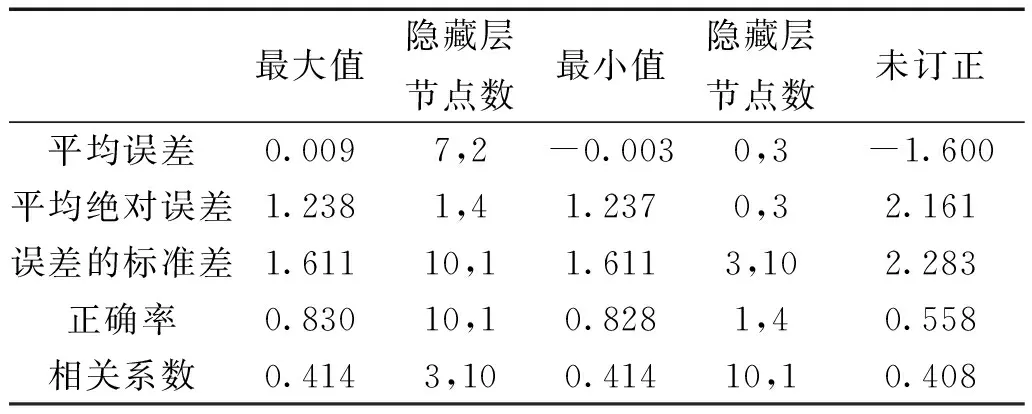
表3 GRAPES模式BP神经网络检验结果Tab.3 GRAPES Model BP-Neural network test results

3.3 JAPAN模式订正及效果检验

JAPAN模式检验中，随机选取了706 563个样本进行训练和建立神经网络模型，运用剩余176 641个样本进行检验。可以看出，运用BP神经网络对风速进行订正后，5个检验数据都有明显的提高。订正后的平均误差的范围在-0.017～0.003 m/s之间，相比未订正过的-0.217 m/s有明显的提高，且平均绝对误差相比为订正的下降0.1 m/s左右，误差的标准差下降0.2 m/s左右，订正后的正确率提高0.06 m/s左右，相关系数改善较小，说明BP神经网络对模式预报的风速趋势变化影响不大。且3种模式中所有神经网络模型中最大值和最小值相差较小，说明对于提高预报正确率和相关系数，隐藏层节点个数影响程度不明显。

表4 JAPAN模式BP神经网络检验结果Tab.4 JAPAN Model BP-Neural network test results

4 结论

本文对目前业务运行中常用的3种数值预报模式风速产品在贵州的预报效果进行了检验，运用平均误差、平均绝对误差、相关系数、误差绝对值和2 m/s的准确率作为检验指标。其中EC模式的预报效果优于另外两种模式，EC模式的平均误差和平均绝对误差较小，说明EC模式预报的离散程度较低。相关系数3个模式相差不大，说明3个模式对风速的变化趋势预报效果相近。但EC模式的2 m/s的准确率明显高于其他模式，故整体而言EC对于贵州省内风速的预报效果较好。

运用BP神经网络对3个模式的风速预报进行订正，订正后的预报效果均有明显改善，其中误差、正确率的改善较为明显，相关系数的提高较小。运用BP神经网络订正后误差和正确率的改善最为明显，订正后的3个模式的正确率均为80%以上，其中GRAPES模式的正确率提升了20%，说明这种订正方法对数值预报的离散程度有较好的改善。但是相关系数的订正效果不明显，说明BP神经网络的订正方式对数值预报风速产品的变化趋势预报效果改进不明显，但总体而言，BP神经网络订正方式对风速的订正效果良好。