齿轮箱振动监测系统

韩 通， 王志华， 陈天佑

(武汉理工大学 能源与动力工程学院， 湖北 武汉430063)

0 引 言

齿轮箱作为机械设备传动系统的重要组成部分，其性能和质量对机械设备有重大影响。其本身若存在缺陷或故障，不仅会影响设备正常运行，而且还会造成财产损失甚至是人员伤亡的重大安全事故。早在20世纪60年代后期有关学者对齿轮箱展开过监测诊断研究工作，其研究发现齿轮箱的振动水平是反映齿轮箱运行状态的良好指标[1]。目前，欧美先进国家已有成熟的诊断分析仪器，如德国的德尔塔分析仪和艾欧尔分析仪，英国ABD(爱彼得)公司的Plato系统等[2]。在国内，大连理工大学的李联玉等研制了基于振动噪声的汽车变速箱性能监测系统。王远程[3]结合阶次分析对齿轮箱进行测试诊断研究。还有不少专家学者基于各种软件开发出振动噪声测试分析程序。齿轮箱振动信号是反映齿轮箱运行状态信息的载体。在实际工作中，对齿轮箱振动信号进行采集并分析处理，提取振动信号特征，可判断是否产生故障及其影响因素，对齿轮箱振动监测分析有重要意义。本文利用LabVIEW软件开发的采集程序和加速度传感器及采集卡等软硬件，分别对齿轮箱正常与故障情况下的振动信号进行采集，然后再通过LabVIEW软件开发分析程序，得出描述时域信号的各种无量纲参数和频谱、阶次谱等，分析信号在频域中的能量分布以及阶次谱中信号对应的阶次。运用振动分析法[4]，有效验证了监测系统的可行性。

1 信号分析方法

1.1 时域分析

时域分析[5]是在时域内对信号进行基本的定量和定性分析。对于振动时域波形，一般有峰值、平均幅值、有效值、方根幅值、偏度、峭度、标准差、均值、方差等指标衡量振动的大小。对于振动信号x(n)，n=1，2，3，…，N，各参数定义如下：

均值：

(1)

最大值：

xmax=max{x(n)}

(2)

最小值：

xmin=min{x(n)}

(3)

有效值：

(4)

标准差：

(5)

方根幅值：

(6)

偏度：

(7)

峭度：

(8)

常用的无量纲参数指标有：波形指标、峰值指标、脉冲指标、峭度指标、斜度指标和裕度指标。同样，设振动信号为x(n)，n=1，2，3，…，N，则式(1)～式(8)各项参数指标计算公式如下：

波形指标：

(9)

峰值指标：

(10)

脉冲指标：

(11)

峭度指标：

(12)

斜度指标：

(13)

裕度指标：

(14)

1.2 频域分析

一般振动信号频率成分丰富，时域波形较复杂，难以通过时域分析全面发现其振动特性，此时需对振动信号进行相关频域分析。频域分析[6]是通过傅里叶(Fourier)变换将信号从时域波形转换为频域波形，即信号随频率的变化情况，并进行相关信号分析的方法，比时域分析更能揭示信号的基本特性。对于信号x(n)，n=0,2,3,…,N-1，通过傅里叶变换得到频谱为

(15)

1.3 阶次分析

为了得到整周期的轴心轨迹，需保证在位移信号采集过程中每转的采样点数一致，这在转速波动较大的情况下难以实现。阶次分析是一种等角度采样的分析方法，将时域内的非平稳信号转换为角域内的平稳信号[7]，保证了位移信号的整周期提取。在振动测试中，当轴的平均转速为nc(单位为r/min)时，其转动基频即阶次谱中的1阶频率为

(16)

其随着转速而变化。频谱图中的某频率f在阶次谱中对应的阶次为

(17)

对角域重采样得到的离散转角序列x(m)进行傅里叶变换可得阶次谱为

(18)

2 试验台及试验方案

2.1 试验台

试验台由输入电机、传动带、减速齿轮箱、磁粉制动器与控制台等几部分组成。图1为齿轮箱的实物图及其结构简图。

图1 减速齿轮箱试验台

2.2 时域分析

在稳定转速情况下，采集两种状态下的振动信号后，分别进行时域分析，得出时域参数，如表1所示。在有量纲参数中，在断齿情况下的振动水平明显高于正常情况，有效值较正常水平增长28.88%。在无量纲参数中，除波形指标外，其他各项指标参数均有明显变化，变化幅度在15%左右，其中峭度指标变化明显，幅度为66.03%，斜度指标的变化幅度则达到130.38%，这是由斜度指标的绝对值较小引起的，说明除波形指标外的无量纲参数指标对齿轮箱发生断齿类故障较敏感。

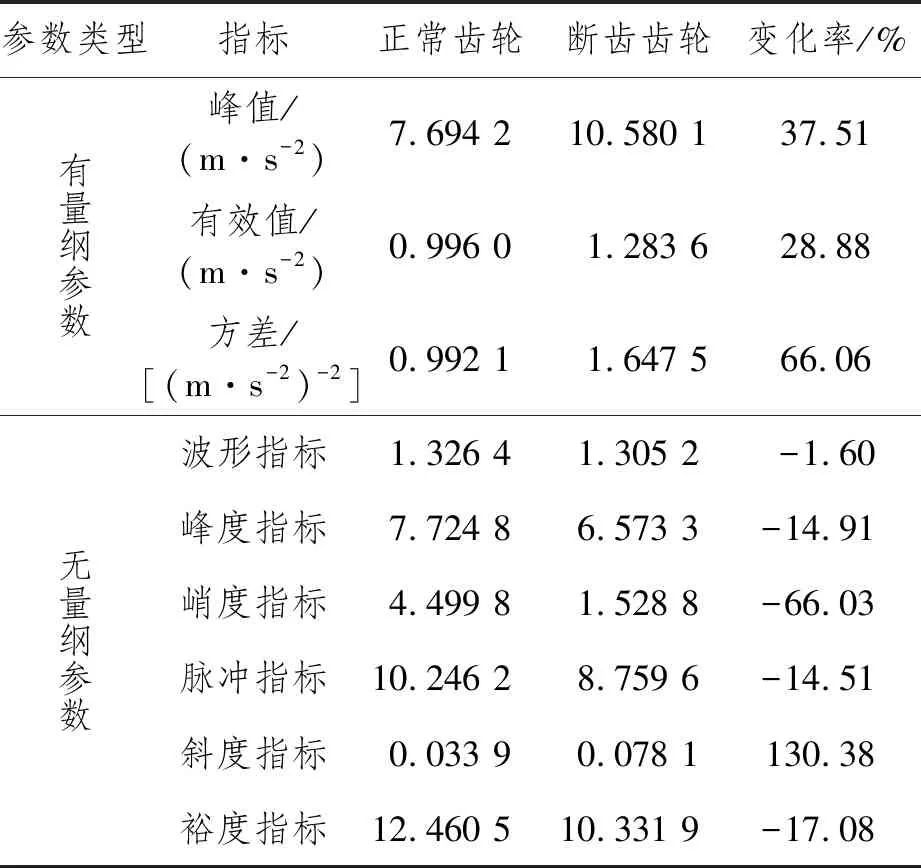
表1 时域特征参数

2.3 频域分析

从频域的角度，分析两种状态下的功率谱，如图2所示。

图2 正常齿轮箱振动信号功率谱

如图2所示，当幅值出现最大峰值为0.000 96时，横坐标所对应的频率为1 164.42 Hz，该频率与齿轮啮合频率相符，并且功率谱在4 657.97 Hz处有一个较小的峰值，为齿轮啮合频率的4次谐波。如图3所示，功率谱上只观察到一个明显的峰值，该峰值对应的频率为齿轮啮合频率，为1 158.40 Hz，对应幅值为0.022 843。在故障情况下齿轮啮合频率对应的振动能量有很大增加，幅值是无故障情况下的23.79倍。频谱的这一变化与断齿的故障特征相符。在频谱上未观察到明显的边频带，无法对故障齿轮进行定位，可使用阶次分析进行进一步处理。

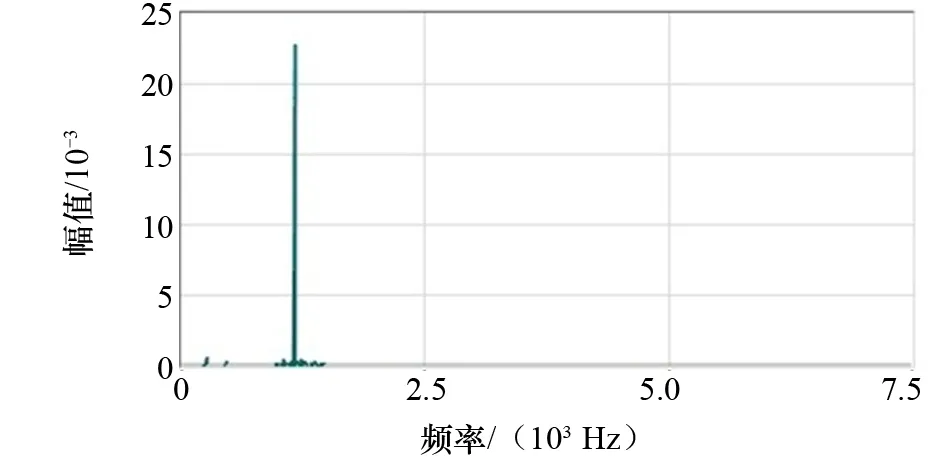
图3 故障齿轮箱振动信号功率谱

2.4 阶次分析

由于试验测试齿轮箱的输出轴转速，可将输出轴转速作为1阶次，结合齿轮箱传动比与齿轮齿数计算齿轮箱各部件的特征阶次。计算结果如表2所示。

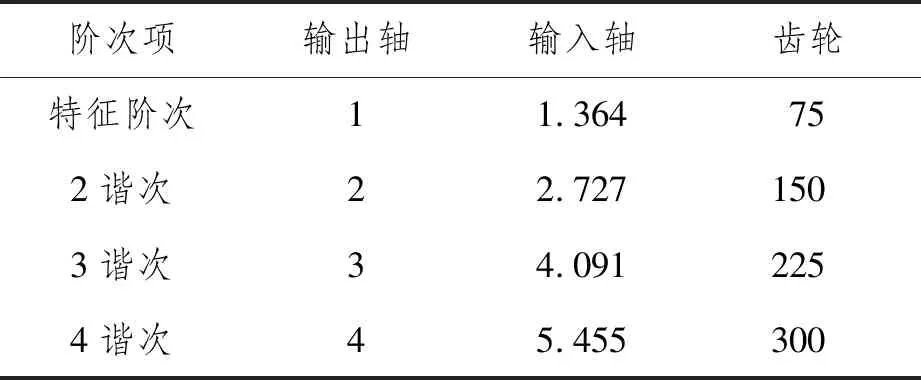
表2 齿轮箱特征阶次 阶

分别对两种状态下的振动信号进行阶次分析，得到如图4所示的阶次谱。

图4 正常齿轮箱阶次谱

阶次谱在75阶次、225阶次、300阶次处有明显峰值，峰值阶次与齿轮的啮合阶次及其谐次对应，在75阶次处的幅值为0.287 104，并且在75阶次附近具有以啮合阶次为中心对称分布的“阶次边频带”。对75阶次附近处进行观察，如图5所示。

图5 正常齿轮箱阶次谱细节

在啮合阶次处有以啮合阶次为中心，以1阶、1.364阶及其谐次为间隔的“阶次边频带”，但“边频”幅值并不对称，这一现象符合齿轮箱振动信号的调制特点。对故障情况下的数据进行阶次分析，如图6所示。

图6 故障齿轮箱阶次谱

当齿轮箱发生断齿时，啮合阶次幅值有很明显增长，可达0.914 968，是无故障时的3.19倍，并且在齿轮阶次的2谐次(150阶次)处出现峰值，幅值为0.044 126，而无故障阶次谱中并不具有这一谐次。因此，从齿轮的啮合阶次及其谐次的变化上可判断出齿轮存在故障。

从图7可知，与正常情况相比，阶次谱在75阶次处有明显的“阶次边频带”，在74阶次、76阶次处出现峰值，与啮合阶次间隔为1阶次，与齿轮箱输出轴的阶次对应，由此可判断出故障位置可能位于输出轴上，即故障齿轮为从动齿轮。

对变速工况下的数据进行阶次分析，并绘制阶次瀑布图，如图8和图9所示。

由于在变速工况下的试验过程是先匀减速再匀加速，两种情况下的瀑布图在啮合阶次(75阶)处的幅值均有先下降再上升的趋势。在正常情况下，由于没有故障，齿轮箱可在变工况下正常运行，各阶次幅值均较小，在高转速时(数据开始阶段与末尾阶段)

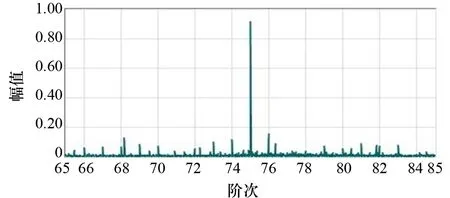
图7 故障齿轮箱阶次谱细节

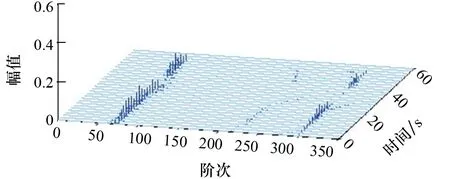
图8 正常齿轮箱阶次瀑布图

图9 故障齿轮箱阶次瀑布图

可观察到除啮合阶次外还有3谐次和4谐次，而在低转速时(数据中段)，各阶次幅值均随转速降低而减小，只能在啮合阶次处找到幅值；在有故障情况下，啮合阶次处的振动能量有很大程度的提升。

3 结 论

分别对齿轮箱在正常运转情况下和有故障运转情况下的振动信号进行采集，通过时域分析，列出各无量纲等时域参数，比较在不同运转情况下参数的敏感性。除波形参数外，其他无量纲参数对齿轮箱发生断齿故障较敏感。频域分析证明故障发生会引起频率所对应的能量分布发生变化。通过阶次分析可判断故障发生的位置。该测试分析结果有效地证明利用振动信号监测齿轮箱的适用性。