浅谈高等数学教育

蒋芬 王丛敏

（广州华夏职业学院，广东 广州 510000）

一、高等数学教育与初等数学教育的区别

高等数学教育与初等数学教育的主要区别体现教学内容，教学受众，思维模式以及应用范围等方面。

（一）教学内容的区别

初等数学教育主要从直观角度出发，关注现实生活当中较常见的数量结构和关联，主要包括集合，简单函数，导数，排列组合，平面和空间几何等。 高等数学教育较多从抽象角度出发，主要内容包括数列、极限、微积分、空间解析几何、线性代数、级数和常微分方程等。高等数学更加注重抽象层面的理论研究，从更深层挖掘数据的结构和关联特性，比如数据改变的快慢，数量发展趋势，n（n≥2）n 维空间向量的关系等。关注抽象是高等数学教育内容的特点，比如四维空间就需要想象和理解能力，因为现实中很难直观感受到。

（二）受众的区别

初等数学的主要受众是思维方式相对比较直观，需要依赖实际应用场景，抽象思维相对还有待发展的低年龄段的小学，初中和高中生。高等数学的主要受众是在接受过初等数学教育，相对而言抽象思维得到一定程度的发展，对于数量关系的思考可脱离实际场景的大专、本科生以及更高思维段的人等。

（三）思维模式的区别

（四）应用范围的区别

初等数学相关知识一般应用在静止的局部环境下，比如具体某次购物下的单价已知情况下的购买量问题，一个具体的相对比较规则几何图形的长度，面积和体积等问题。高等数学是从动态的发展的观念来看待问题，思考的是更加一般的数量关系，从宏观和微观层面对数量关系进行研究，这种宏观或者微观一般属于理论情况，比如研究给定假设条件下传染病的感染人数的发展规律，某种大豆，石油等商品的价格对于外汇变化的敏感度等。

二、初等数学与高等数学的联系

初等数学中一般直接对方法进行运用，对概念进行讲解。初等数学中讲到能化成分数的数是实数，对分数化成小数是非常简单的，但是反过来对无限循环小数如何化成分数却没给予说明。

高等数学对以上初等数学的结论给予证明。极限思维中有“无限逼近既相等”这样的理论支持，比如循环小数0.9=1是直接可证，令0.9=x，则9.9=10x，两式联立相减得9=9x，即可推得0.9=x=1。

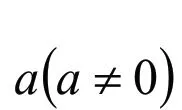
高等数学对知识结构提示进行了补充。在初等数学当中讲到数据存储结构集合，集合具有无序性，集合元素不重复。高等数学中的矩阵其实是对数据存储结构的补充，矩阵是有序结构，矩阵元素可重复。

另外初等数学的方法研究数量变化的增减性、凹凸性、求极值、最值等种种特性有很大的局限性。在高等数学中利用极限、导数、级数等知识可用比较完备的方法研究函数的特性，从总体上以一种的动态的观念研究抽象的数量关系和关联结构。

三、关于高职高等数学教育建议

高职院校的学生从实情况上来，其在初等数学教育过程中数学素养相对有待低声。受众的基础差异性，以及职业培养的目的性决定了高职高等数学教育的课程制定应该具备自身的特点。

（一）遵循适度原则

首先，需要针对职业类教育理工科的共同需求对公共需求部分进行讲解。公共模块知识主要集中在简单的一元函数微积分，一元函数微积分是定量研究连续变化的严格的逻辑体系，包括定义数量关系的一元连续函数，连续变化的快慢，变化量大小等。对一元函数微积分的理解直接对多元函数微积分的学习有着非常重要的作用。由于高职学制和职业教育目的特点，高职高等数学的公共部分适度倾斜对一元函数微积分的讲解，而多元函数相关知识根据专业需要进行讲解。

（二）遵循够用原则

,职业教育是直接为社会培养专业技术人才的，所以教学内容上又要遵循够用原则。这要求根据各专业的特色讲解职业方向相关数学知识，比如管理学相关专业可以增加线性代数部分和统计学相关知识讲解，计算机专业可针对性地讲解数论基础知识，建筑学专业可进行微分方程的讲解等。通过区别化的讲解，提升学生的数学素养和专业素养，将数学工具化，培养具有数学素养的职业人才。

（三）遵循发展的原则

职业教育重点是职业人才的培养，也要遵循终身教育的要求，高等数学教育需要对于职业后继续发展提供数学基础，这种数学基础主要是指数学思的培养，能够在职业要求促使下运用数学解决实际的问题。发展的原则要求高等数学的教学内容的知识框架非常熟悉，对于前后相关知识点进行适度引导，为职业后的发展提供方向指引。

四、总结

基于初等数学教育和高等数学教育的差异性和联系，在高等数学学习的过程中，高职类院校应该充分把握专业需求，制定合适的教学大纲。作为受众的具备一定抽象思维的职业教育学生应该多思考高等数学与初等数学的联系，从一个更新的角度去审视所学过的知识，学会融会贯通。其次要多审视自己的专业特点以及专业对数学的要求，有目的性的选择需要关注的专业数学方向。