基于实验室预约机制算法的对比分析

董萃莲，董海峰

（西安石油大学计算机学院，西安710065）

0 引 言

随着高校信息化综合体制的不断改进，对学生实践能力的培养也已然成为一个长期追求目标。与此相关的实验室预约排课问题［1］即已成为一个广受关注的热点探讨内容。但由于实验室预约排课研究是NP完全问题［2］，且容易受到多种因素的复杂影响［3］，因而就陆续涌现了不少基于实验室预约排课问题的算法，比如：遗传算法［4］、蚁群算法［5］、课元算法［6］、图论算法［7］、专家系统算法、模拟退火算法［8］、背包算法［9］等。

1 实验室预约问题

实验室预约主要是用于学生集中式预约和自主式预约，学生可以随集体预约实验，也可自主预约实验。一般情况下，自主预约的实验不分配老师。对于集中式预约实验，不同专业、不同年级、不同班级的学生有可能选择一个实验项目，在此种情况下根据课程情况指派相应的实验室和辅导老师，为了使实验室器材资源可以物尽其用，能合理地安排老师指导学生实验，协调实验室、学生、老师三者之间的各种利益需求，使得学生可以受益最大化，实验室资源利用率最大化［10］；再者，对于自主式预约实验，为减少学生预定了实验后失约而造成实验室资源的闲置和浪费，以及其它有此需要的学生还未能及时预约实验的现象［11］，这里拟将针对基于背包算法［12-13］和模拟退火算法在实验室预约机制的性能优劣上做出分析对比，详情展开如下。

2 算法分析

2.1 背包算法

背包算法［14-15］可以理解为给定一些物体，每个物体都有自己的重量和价值，在一定的总重量之内，应如何进行择取，能使得物品的总价值最大［16］。

假定实验室数为N，实验室的编号设为k（k小于等于N），每间实验室可容纳人数在此设一固定值，一项实验进行的人数分值为p［i］（i为项目数），人数分值等于人数值、即一人为一分，设定老师指导权重分值为 t［i］，因此有老师指导的情况设定 t［i］初值为2分，否则为1分，设一项目实验的实验学术评估分值为a［i］（即每个项目的学术评估分值），以此来区分每个实验项目的学术价值和重要性，该项基础分值为1分，每隔0.5分作增减，设定实验的综合需求分为z［i］，设定时间段的受益总分值为w（其初值设定为0）。在学生自主预约实验室时，基于集中式预约实验室增加一个信誉度的参数c［i］，每个学生的初始信誉度设置为10，每失约一次信誉度减1［17］。

2.1.1 预约实验室的算法研究

（1）集中式预约实验室的设计分析

①情况一：如果该项目人数大于实验室可容纳人数，则：

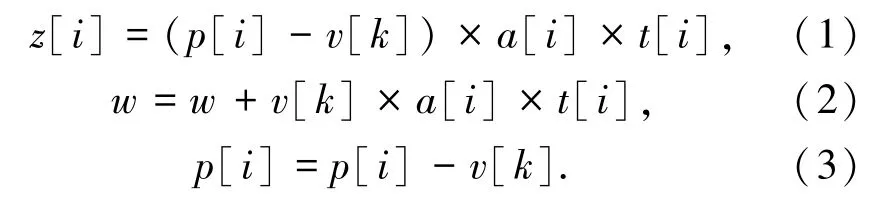
②情况二：该项目人数小于实验室可容纳人数，则：

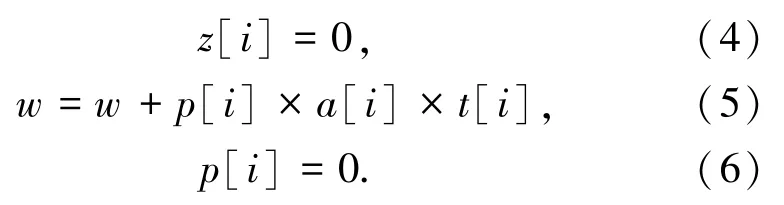
（2）自主式预约实验室的设计分析

①如果该项目人数大于实验室可容纳人数，则：

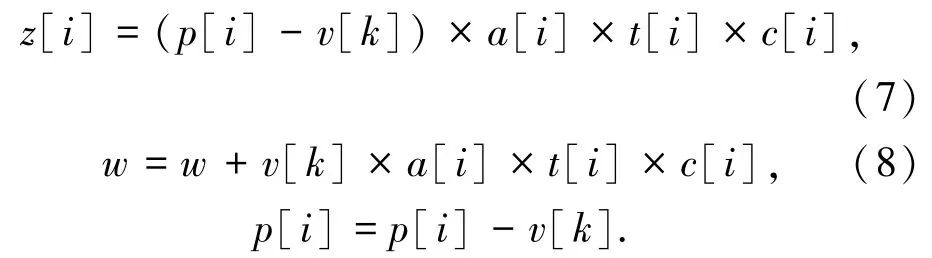
②该项目人数小于实验室可容纳人数，则：

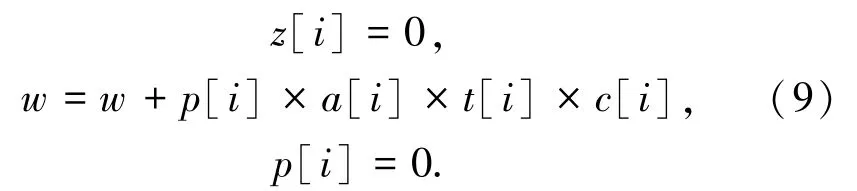
2.1.2 基于实验室预约的背包算法［18-19］

Step 1计算出一个时间段中每个实验项目的实验综合需求分。

Step 2找出实验综合需求分中最大的实验项目。

Step 3对实验综合需求分最大的实验项目分配实验室，如果预约该实验项目的学生人数大于一个实验室的容纳人数，则按公式（1）更新该项目的实验综合需求分，按公式（2）更新受益总分，更新该项目的总人数，否则将该项目的实验综合需求分置为0，按公式（5）更新该项目的受益总分，更新该实验项目的总人数为0。

Step 4用更新后的值代替原来的，重复Step 2～Step 3。

Step 5当已有实验室已经安排满或者实验综合需求分最大为0，则终止循环。

至此，研究可得到背包算法的设计流程如图1所示。在实验室没有排至满额的情况下，空闲的实验室可以作为学生自主学习的实验室用，但不对其分配老师进行辅导、也不设定限制，学生可依据自己的时间安排在工作日内随时去进行实验。预约情况将进行统一集中公布，没有预约成功的学生可以转入下一轮的预约，但却需要提前数周来申请预约。在某些时间段若发现预约实验室的人数很少，此时会有很多闲置的实验室，为此即可将下一时间段或者预约人数较多的时间段的实验项目调配转换至此空闲时间段内，只是在该种情况下还需要对程序做出一定的修改［20］。

综上分析［21］只是对集中式预约实验提供了算法描述，自主式预约实验室的算法在计算实验项目需求分和受益分时需要引入信誉度分进行相应的换算，在此不作赘述。

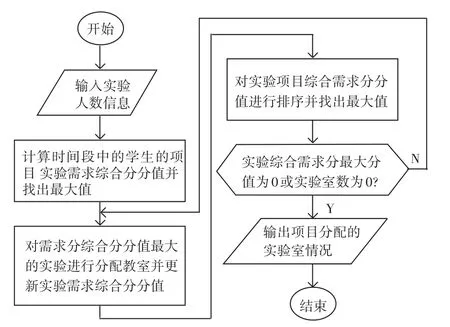
图1 背包算法流程图Fig.1 Knapsack algorithm flow chart

2.2 模拟退火算法

模拟退火算法［22］是以某一比较高的初温为出发点，伴随着温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。模拟退火算法［23］包括3个函数、2个准则，分别是：状态产生函数、状态接受函数、退温函数、以及抽样稳定准则和退火结束准则。

假设实验室的预约排课的周期为一周，本次研究则致力于将一个实验项目集安排到一组时间和一组实验室中。设实验项目集Xi为第i项实验，Pi表示指导教师，Si表示实验项目的学生数量，时间段Tm表示一周中的实验时间划分，Rk表示实验室编号（且设实验室可容纳学生数为固定值），Lin表示某项实验Xi安排的实验时间段组，G（S）表示目标函数，故而，此问题的最佳解决方案可表示为：S（Lin，Tm，Rk）。

由此，可推得基于实验室预约的模拟退火算法的设计流程如图2所示，对其流程步骤可阐释解析如下。

Step 1设置初温T0，初始解S，预设迭代次数为L，计算目标函数G（S）。

Step 2扰动生成新解S∗，计算目标函数G（S∗）。

Step 3计算目标函数的增量ΔG＝G（S∗）-G（S）。

Step 4当目标函数的增量大于0时，按照Metropolis准则［24］选择新的解，否则以当前解S∗为当前新解。

Step 5当未达到预设迭代次数时，返回Step 2，否则进入 Step 6。

Step 6判断是否满足停止条件，若未满足，则降低温度返回Step 2，否则，迭代结束，返回最优解S∗。

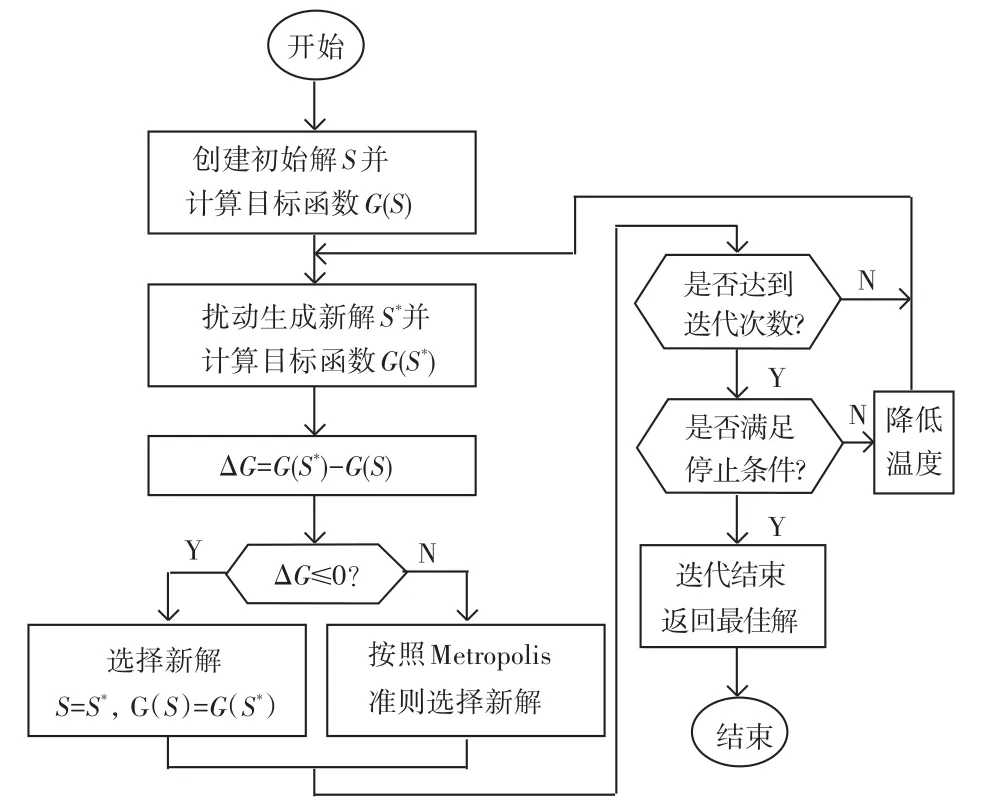
图2 模拟退火算法流程图Fig.2 Flow chart of simulated annealing algorithm

3 算法的对比分析

考虑到前文2种算法对于实验室预约排课时的着重点各有不同，即使用于同一约束条件下的实验室项目预约，得到的结果也未必一致。因此，需要根据实际情况加以选择性使用，对比分析［25］这2种算法的优缺点后，对此内容可分述如下。

（1）算法机理对比。背包算法分2种情况考虑，在学生自主预约实验室时，加入了信誉度参数，从而约束学生使得实验室资源尽可能地不被浪费，而模拟退火算法中是对大集体的实验室预约的排列求解，并未充分考虑到学生的自主性。

（2）算法复杂度对比。背包算法［26-27］的算法复杂度为2，模拟退火算法的复杂度为5，相比而言模拟退火算法的实现难度较背包算法大。

（3）算法应用范围对比。此处的背包算法比较适合于解决小型的实验室预约安排，范围相对较小，而此处的模拟退火算法比较适合相对大型的实验室预约安排。

（4）涉及因素对比。2种算法的考虑因素都是多重的，对于参数的选择有所不同。

（5）算法的适用性分析。2种算法常常是围绕某一场景问题来进行相应设计，通用性较差。

4 结束语

本文中，对于以上2种算法的学习分析主要是基于实验室预约机制的环境模拟［28］，缺乏相对深入的数学推理分析论证。但对于解决同一类型问题的各种算法［29-30］，这些算法往往各具特色，不能一概而论，需根据具体情况给出具体分析。有时，可用一种算法解决某类问题，而在其它时候则可用多种算法结合的方法来解决另一类问题，以求得到最佳设计方案。