柔性关节机器人的自适应稳态控制算法

田小玲

（广东工业大学华立学院，广州511325）

0 引 言

柔性关节机器能模仿人类和动物的关节进行自主运动，并在机械臂设计、下肢助力外骨骼以及智能仿生腿设计等领域都具有很好的应用价值。柔性关节机器人在运动中会受到参数摄动、外界干扰及未建模动态等不确定性因素的影响，导致机器人的控制系统引入柔性元件构成执行部件时将产生稳态误差，机器人的姿态调节性能不好，需要进行柔性关节机器人的自适应稳态控制，提高柔性关节机器人的输出稳定性［1］。

传统方法中，对柔性关节机器人的自适应稳态控制方法通常建立在模糊PID控制器的基础上，结合滑模控制方法进行机器人的位姿参数调节和自适应控制［2］，取得了一定的控制效能。 其中，文献［3］中提出一种基于时滞反馈的柔性关节机器人仿生步态鲁棒性控制方法，采用传感器基阵进行柔性关节机器人的步态相关性参数采集和稳态跟踪融合处理，提高机器人的自适应位姿参量调节能力，但该方法的控制时滞较大，自适应规划性能不好。文献［4］中提出采用时滞反馈补偿方法进行柔性关节机器人的控制误差修正，提高柔性关节机器人的稳态控制性能，降低稳态误差，提高柔性关节机器人控制的稳健性，但该方法的计算开销较大，实时性不好。文献［5］中提出一种基于能量反演参数自整定修正的柔性关节机器人步态融合跟踪控制算法，采用模糊PID进行自适应修正，提高了柔性关节机器人步态的抗扰动性，但该算法需要大量的姿态先验数据和规则作为引导，在先验信息缺乏的时候，控制效果不好。针对上述问题，本文提出一种基于多模式弹性驱动的柔性关节机器人的自适应稳态控制算法。首先构建柔性关节机器人末端位姿参数分布模型，分析柔性关节机器人位姿调节的约束参量，将柔性关节机器人位姿调节的稳态控制问题转化为机器人位姿参量自适应调节问题，有效实现柔性关节机器人的姿态变换的特征分解和误差补偿修正。然后结合运动规划模型实现机器人的多模式弹性驱动，完成柔性关节机器人位姿调节稳态控制。最后进行仿真实验分析，展示了本文方法在提高柔性关节机器人的自适应稳态控制能力方面的优越性能，得出有效性结论。

1 柔性关节机器人控制约束参量分析及动力学模型

1.1 柔性关节机器人控制约束参量分析

采用多模Kalman滤波融合方法进行柔性关节机器人的末端位姿相关性参数采集，进行控制约束参量分析，在柔性元件形变状态下通过多传感器融合跟踪方法进行柔性关节机器人的位姿参数拟合分析和回归分析，采用闭环系统反馈修正方法进行反馈力学误差的补偿［6］，采用连杆端动力学控制方法，用k∇H（θ）取代，得到柔性关节机器人的力学稳定性控制律写成：

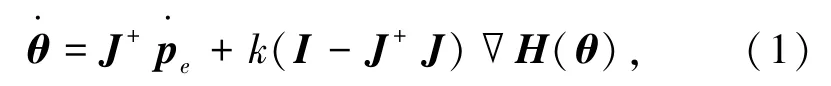
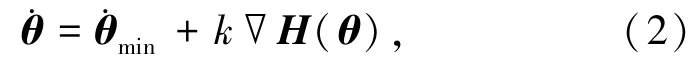
其中，电机与连杆之间有转角差最小范数解为：

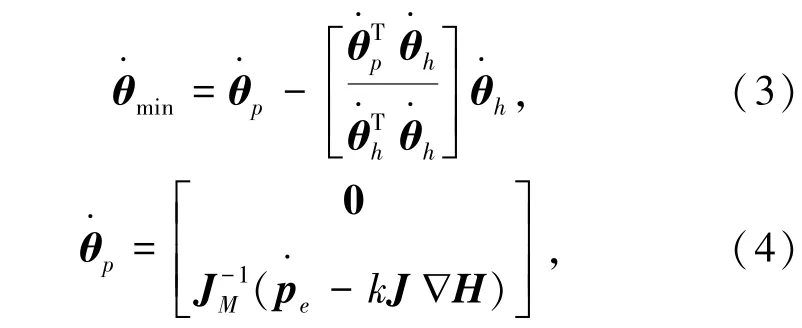
上式表示的一个特解为的一个齐次解。构建一个线性时变系统对柔性关节机器人末端位姿轨迹进行动力学平衡拟合，假定某时刻真实的柔性关节机器人仿生不同姿态角为β∗＝V（k）1Σ（k）1-1U（k）1TY（k）， 其中V（k）1、Σ（k）1和U（k）1为X（k）表示柔性关节机器人有效惯量之间的SVD运算解算结果，连杆在到达目标位置的近似特征量为e-Lms＝1-Lms。 在系统的核空间矩阵中，引入前馈补偿设计，利用高度非线性的PI控制器进行柔性关节机器人的末端位姿稳定控制［7］，选择一个时滞耦合系统作为柔性关节机器人的被控对象， 当传递函数确定时，Gm（s）＝G0（s），tm＝τ， 柔性关节机器人的末端位姿跟踪系统的反馈信号为：

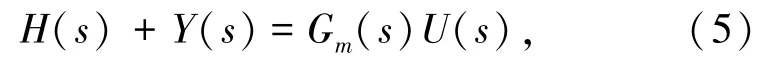
采用固定控制器+增益规划（Gain-Scheduling）的控制方案，对柔性关节机器人的测距路线进行自适应规划，采用多传感器信息融合方法，测量柔性关节机器人的驱动力学分布集，得到姿态传感传递函数：

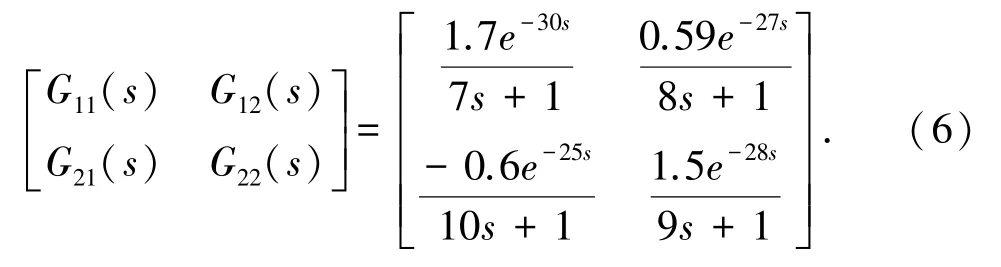
其中，控制器的输入特征量从Gm（s）的输出端引出了反馈信号，实现机器人的位姿自适应调节。

1.2 机器人控制的动力学模型

求得柔性关节机器人速率陀螺仪的跃阶响应，通过转动惯量的动量矩特征分析，构建稳态方程实现柔性关节机器人末端位姿稳定性控制，得到柔性关节机器人的驱动力学力学稳定控制满足如下约束条件：

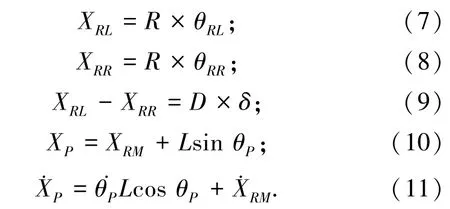
选取柔性关节机器人输入状态变量为x＝［φ，，θ］T， 通过构造一个拟合关系，采用非线性严格反馈误差修正方法进行测量误差修正，得到柔性关节机器人的测量方程表示为（x，u），由此构建的柔性关节机器人力学稳定性控制过程是一个多变量、非线性、强耦合系统，结合非线性动力学驱动控制方法［8］，进行控制约束参量分析和优化求解。对柔性关节机器人末端位姿姿态进行融合跟踪和自适应参数调节，得到柔性关节机器人末端位姿轨迹跟踪控制系统满足如下非光滑时变函数：

根据线性化小扰动的优化条件，当x（t）＝[x1（t），x2（t），…，xt（t）]T表示的扰动向量误差矩阵收敛时，柔性关节机器人的控制约束参量具有自相关性，由此将柔性关节机器人位姿调节的稳态控制问题转化为机器人位姿参量自适应调节问题。

2 控制律的优化设计

2.1 柔性关节机器人的姿态变换与误差修正

构建柔性关节机器人末端位姿参数分布模型，分析柔性关节机器人位姿调节的约束参量，采用姿态传感器得到观测的柔性关节机器人末端位姿姿态数据矢量z(t)的协方差矩阵可以表示为：

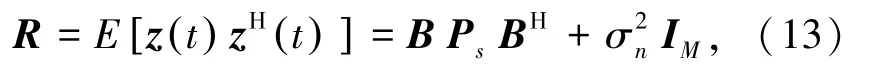
结合时滞耦合控制方法构建柔性关节机器人仿生末端位姿的模糊控制器，姿态传感序列输出为则陀螺仪上的外力矩控制方程可以改写成：

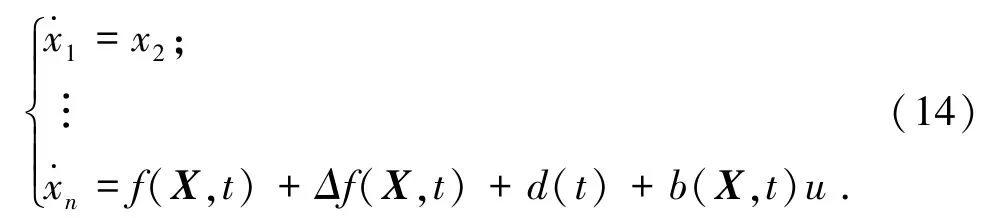
设定控制目标方案为ϑ，ϑ＝（θ1，θ2，…，θn），反馈线性化的控制函数pi（t）为：

在对机器人的实际控制过程中，根据不同的工作模式需求进行更换，利用弹性元件达到减振和姿态调节的目的。

2.2 多模弹性驱动的控制律优化

采用闭环PI型迭代学习方法实现柔性关节机器人步进控制的约束参量分析［9］，在一个运动周期内，机器人的稳态跟踪控制方程为：

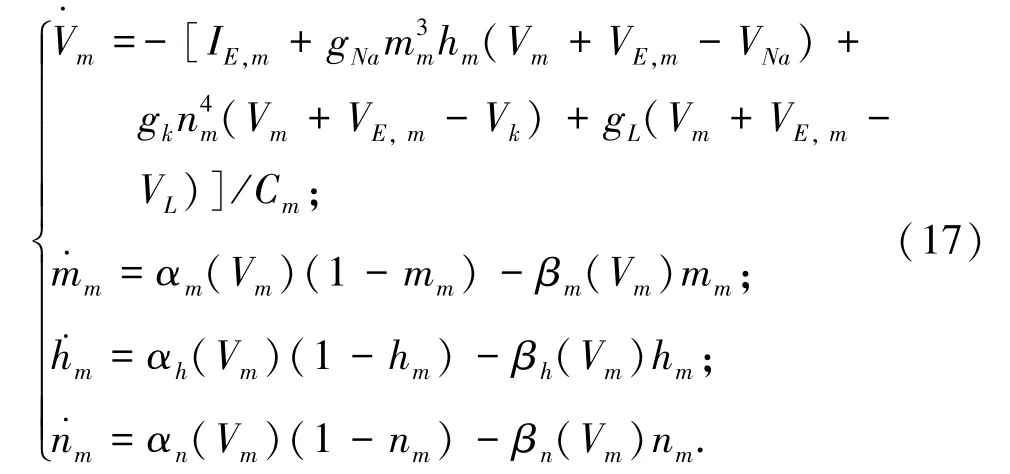
构建仿生柔性关节机器人的被控对象模型，以仿生柔性关节机器人质心在地面上的投影作为坐标系的原点，在每一次迭代中，输入为柔性关节机器人的姿态观测向量Y（i），可得机器人的刚性驱动特征量为：

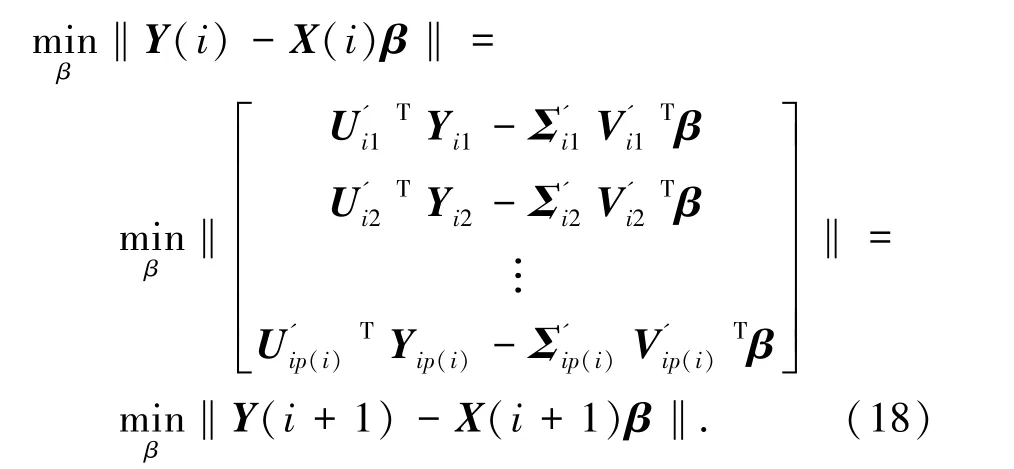
记Xij的柔性驱动模式的秩为rij，rij≤m，则和的串联弹性驱动输出特征量分别为rij×rij，Nij×rij和m×rij， 对矩阵解进行酉分解，得到X（i+1）和Y（i+1）的行数，表示机器人的自适应控制的模态数：

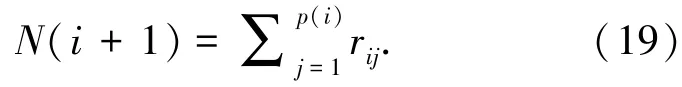
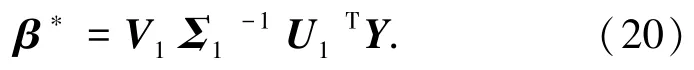
其中，扰动观测量为Σ∈Rn×m， 且Σ＝diag（δ1，令：

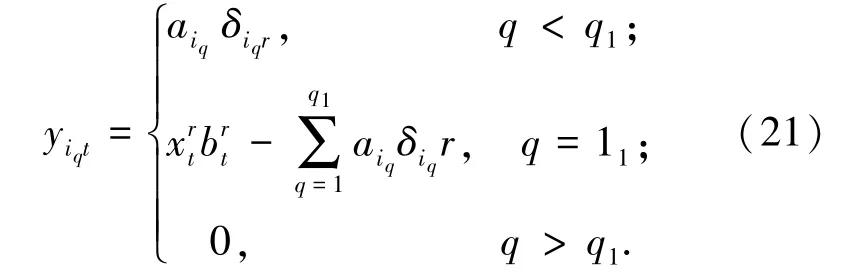
当j≠t时，结合运动规划模型实现机器人的多模式弹性驱动，完成柔性关节机器人位姿调节稳态控制，得到控制律稳定解的约束条件为：

根据上述控制律的优化设计，实现柔性关节机器人的自适应稳态控制。

3 仿真实验与性能分析

为了测试本文方法在实现柔性关节机器人的自适应稳态控制和姿态调节中的应用性能，进行仿真实验，实验采用Matlab进行算法编程设计，构建自适应控制律，采用LabVIEW RT进行控制系统设计，机器人的柔性关节系统采用Maxon EC-4Pole30和Maxon EC-4Pole22直流伺服电机设计，结构如图1所示。

以图1的柔性关节机器人为研究对象，设计关节力矩为12 N·s，对关节的力学参数采集的样本数为2 000，训练集为100，机器人带有 0.86 kg的负载，根据上述仿真参量设定，进行机器人的位姿稳态性控制，得到机器人的位姿参量的控制输出结果如图2所示。

图1 机器人的结构模型Fig.1 Structure model of the robot

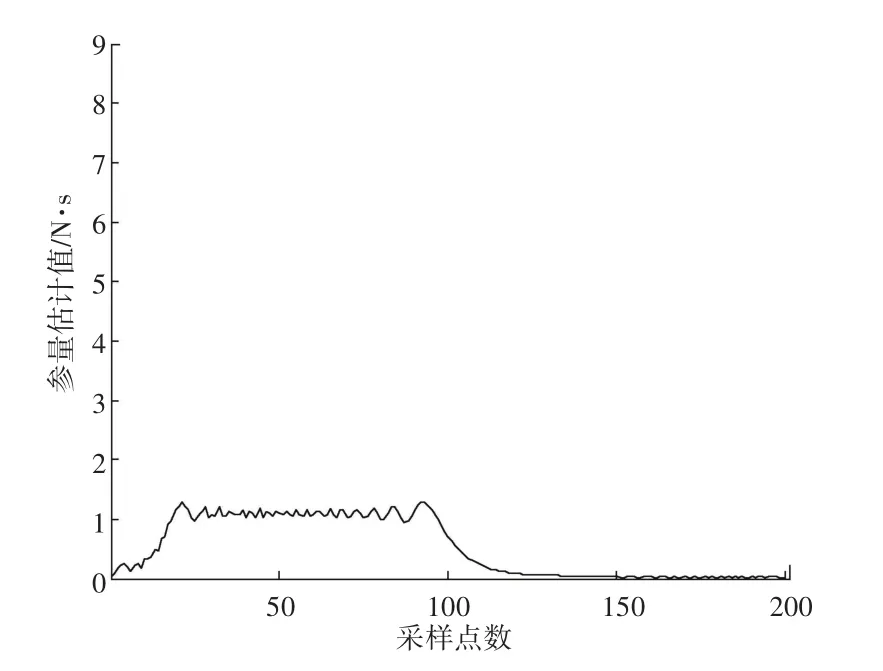
图2 机器人的位姿参量的控制输出结果Fig.2 The control output of the robot＇s position and attitude parameters

分析图2得知，采用本文方法进行机器人位姿调节的稳态控制和收敛性较好。测试控制性能曲线，并与传统方法对比，得到结果如图3所示。

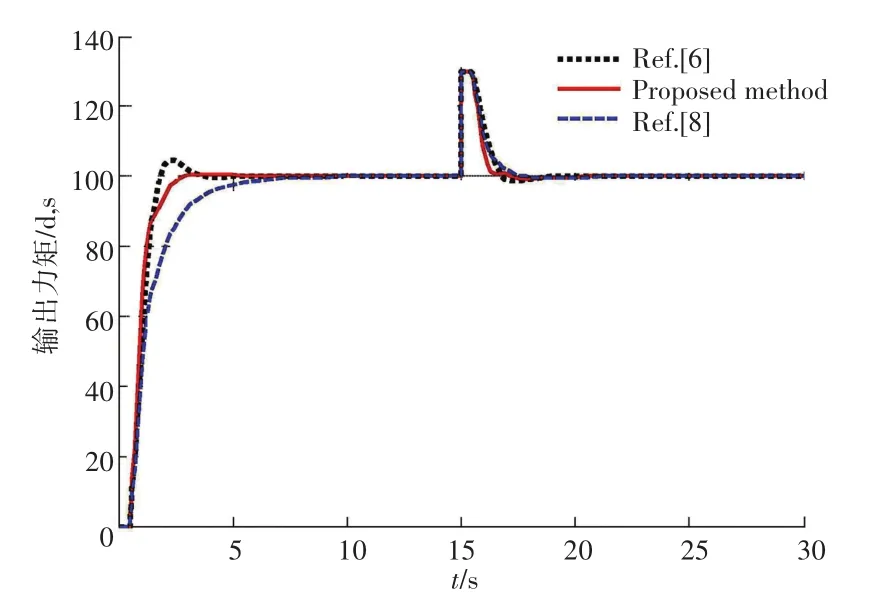
图3 控制性能对比Fig.3 Control performance comparison

分析图3得知，采用本文方法进行柔性关节机器人位姿控制的稳定性较好，自适应性能较好。

4 结束语

柔性关节机器人在运动中受到参数摄动、外界干扰及未建模动态等不确定性因素的影响，导致机器人的控制系统引入柔性元件构成执行部件时产生稳态误差，为了提高机器人姿态稳定性，本文提出一种基于多模式弹性驱动的柔性关节机器人的自适应稳态控制算法。构建柔性关节机器人末端位姿参数分布模型，分析柔性关节机器人位姿调节的约束参量，有效实现柔性关节机器人的姿态变换的特征分解和误差补偿修正。结合运动规划模型实现机器人的多模式弹性驱动，完成柔性关节机器人位姿调节稳态控制。研究得知，本文方法进行机器人控制的稳态性较好，收敛性较强。