一种面向传感云的数据源质量评估框架

王 琳

（哈尔滨工业大学计算机科学与技术学院，哈尔滨150001）

0 引 言

劣质数据会严重影响各类数据驱动的服务的质量。近年来，数据质量的研究受到了人们的广泛关注［1-2］。在一些多数据源的应用中，如无线传感器网络和物联网，每个实体的值通常会在不止一个数据源处得到提供，但来自不同数据源的数据却存在着偏差。数据质量控制是基于传感器的系统中需要解决的重要问题之一［3］。当前，随着传感云（sensor-cloud）［4］的兴起，在很多场景下，人们更倾向于将传感器的数据传至云端处理。这样云端便累积了大量的历史数据。基于这些历史数据，并借助云服务的计算能力，就可以评估数据源的质量，从而，当同一实体的来自不同数据源的数据存在偏差时，可以根据数据源的质量来确定哪些数据可被进一步用于数据分析和回答查询。

传感云环境下，数据源的质量评估可以带来下述2方面的收益。首先，如果能够预先知道数据源质量，可以在传感器推送数据至云端、云端将数据存入数据库时做出质量标记（可以类比为店铺信用），在之后的应用中，如果需要快速返回一个查询结果，就可以无需再遍历所有数据，而直接读取高质量的数据源的数据来回答查询。研究可知，遍历和计算需要花费的时间和消耗的计算资源均要高于直接读取数据，因此当查询频繁到达时，该方式可以节省大量资源。其次，如果应用或查询需要即时从传感器中提取数据，那么在获知数据源质量之后，提取数据时将可直接忽略低质量的数据源，这样不仅可以避免劣质数据污染查询结果，而且也可以节省网络带宽等资源；甚至，还可以不要求全部传感器都返回结果，而是直接要求在当前场景下会返回高质量数据的某一个数据源返回数据，此时的其它节点就不用采集和返回数据，如此也可以有效节省能源。

这里，研究还给出了一个传感器网络中数据源质量评估的具体示例，详情如下。

例1图1所示为不同时刻3个数据源关于3种污染物指数的测量值，其中列名k_pm1、k_pm25、k_pm10表示k号数据源返回的pm1、pm2.5和pm10的测量值，t列表示时刻。假设有多个数据源，为了简便，选取3种污染物指数，在不同时刻的均值如图2前三列所示，数据源测得污染物指数与均值的最大绝对偏差值如图2后三列所示。对图1中的每个值，研究采用相对偏差作为数据质量的度量。设值v对应的属性为A，则v的相对偏差＝1-abs（vavg_A）／d_A，其中avg_A和d_A分别为属性A的均值和最大绝对偏差。同时，研究也对图1中的每个值都计算数据质量，得到的质量评分结果如图3所示。

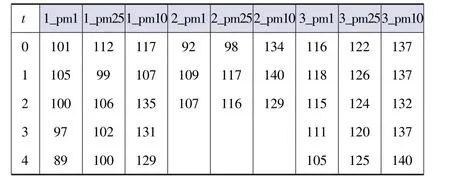
图1 原始数据集Fig.1 The raw data set

图2 各属性平均值和最大绝对偏差Fig.2 The average and maximum absolute deviation of every attribute

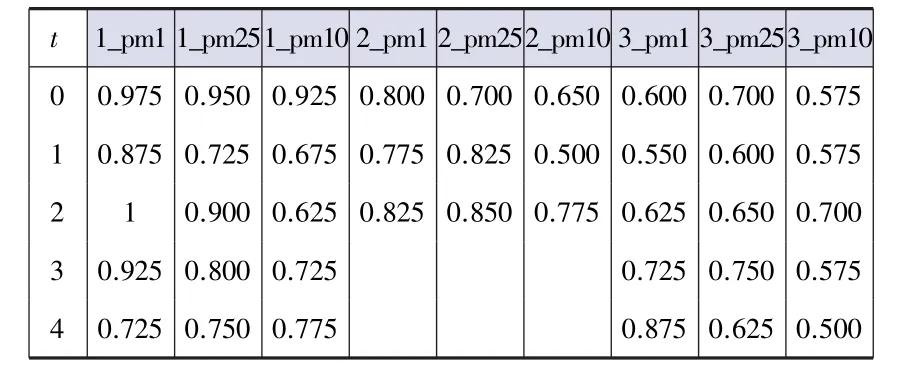
图3 质量分值结果Fig.3 The result of quality score

从图3中可以直观看出，不同数据源的质量存在着明显的差异。例如，对1号数据源来说，其数据在0时刻3个属性的值的质量均较好，在1～3时刻pm1属性值较好，但pm25和pm10属性值的质量较为一般，在4时刻3个属性值的质量均不理想。对2号数据源来说，其0～2时刻有数据，且3个属性上的值差异不大，在3～4时刻却存在着数据丢失。3号数据源则只在时刻4提供过一次较好的pm1值，其它时间质量均不理想。由此可见，即使是同一个数据源，其质量也存在着随时间和属性波动的情况，因此，用单一的值来描述一个数据源的质量有失偏颇，研究需要寻找更为规范合理的质量描述。

基于历史数据，为了能够切实评估数据源质量，本文拟展开多个方面研究。对此可阐释如下。

首先，定义了数据源质量矩阵，用于描述一个数据源在不同条件下的质量情况。

其次，给出了质量矩阵的计算框架。基于该框架可以对每个数据源计算其质量矩阵，且用户可以调整平衡参数来改变质量矩阵对于数据源质量描述的细致程度。

最后，在真实数据上进行了实验。实验结果表明，本文提出的质量矩阵定义及其计算框架能够有效地评估数据源的质量。

综上所述，本文的研究内容可安排组织如下：首先介绍相关工作；然后论述了问题定义；再次则提出质量矩阵的计算方法；接下来给出了实验结果；最后就是本文研究结论。下面，针对各部分研究将展开分述如下。

1 相关工作

当前，很多研究都在探讨基于约束的数据质量判定［1-2，5-6］。也就是说，这些工作均围绕着当给定一个数据集合时，应如何判定其中每个值的数据质量。而与本文研究的不同之处就在于，这些研究仅是关注单个值的数据质量，却没有指出应如何基于每个值的数据质量来综合度量整个数据源在不同条件下的质量。因此，这些工作也只可作为本文研究的支撑。

另一方面，数据融合和真值发现则研究如何从多源中找到高质量的数据［7-9］。在设计时考虑了如何根据来自不同数据源的各类错误来发现各个数据源之间的依赖，而且可凭借数据源间的依赖关系寻找被查询属性的最新值。这些工作虽然可以用来评估数据源质量，但其更多地仅是着眼于当数据源之间存在拷贝依赖关系时，该如何找到数据的最新值。而在传感云环境下，不同传感器采集数据可以被认为是独立的，不同数据源也不存在拷贝依赖，其值之间的相似性不会来自于互相拷贝，因此，需要研发专门的方法来评估这种场景下的数据源质量。

2 问题定义

设S＝｛s1，…，sn｝是数据源的集合，T＝｛t0，…，tm｝是时刻的集合，dk是数据源sk提供的各时刻采集的数据集合。Q是一个质量度量函数，Q（v）是值v根据度量函数Q计算得到的质量分值。

根据Q，针对数据源sk可计算得到Dk中每一个值的质量分值。举例来说，对例1中的1号数据源，研究可以基于相对偏差这一质量度量，得到如图3中1_pm1、1_pm25、1_pm10这3列所示的质量度量结果。

过程中，将这样的质量评分结果称为原始质量矩阵。令QM（dk）表示由Dk计算得到的质量矩阵，则QM（dk）和dk具有相同的行数和列数。而如例1中所言，不同的数据源在各时刻、各属性上表现出质量差异的同时，也在一些时刻或属性上表现出一定的质量上的共性。例如例1中的数据源在时刻1～3提供的数据就表现出质量上的共性。因此，为了清楚地描述数据源在不同场景下数据质量的差异和共性，研究还需要对原始质量矩阵做一些调整，即合并具有共性的行、同时区分具有差异的行。由此，本文要研究的问题的形式化定义表述见如下：

输入：数据源集合S＝｛s1，…，sn｝，时刻集合T＝｛t0，…，tm｝，数据集集合D＝｛d1，…，dn｝，质量度量函数Q

输出：abbr（QM（d1））， … ，abbr（QM（dm））

其中，abbr（QM（dk））是QM（dk）化简后的结果。

化简质量矩阵有2个好处。首先，化简后的矩阵较原始矩阵来说，更能够突出数据源在不同场景下数据质量的差异和共性。其次，当数据量很大时，存储原始数据已经消耗了大量资源，再消耗同样多的资源来存储质量矩阵显得并不现实，而只要化简得足够充分，那么化简后的质量矩阵可以大幅节省存储资源，同时，对化简后的质量矩阵进行访问的时间开销也远低于访问原始质量矩阵。在下一节中，将详尽探究质量矩阵化简方法的研发与设计。

3 质量矩阵化简方法

给定质量矩阵QM（dk），研究对其进行化简的设计思想如下：对原始质量矩阵QM（dk）和数据源sk，分别计算QM（dk）的相邻两行数据质量分数向量的相似度，同时，根据用户给定的阈值θ，如果距离不超过θ，则合并两行为一行，并用两行的均值填充该行。流程步骤见如下。

Step 1自上向下扫描QM（dk），设当前扫描到第r行，计算r行和r+1行的相似度Simr，r+1。

Step 2判断Simr，r+1是否小于θ，如果是则进入Step 3，否则进入Step 4。

Step 3合并r和r+1行得到新的r行，计算新的r行和r+1行的相似度Simr，r+1，跳转Step 2。

Step 4扫描继续，跳回Step 1。

在此基础上，将使用例2来说明例1中的原始质量矩阵的化简过程，其主旨要点可概述如下。

例2假定给定阈值为0.1，以图3的1号数据源为例，研究选用向量的归一化距离来度量行的相似度，合并策略选取计算均值。在0，1两时刻的质量评分向量的归一化距离为0.202 587，不合并。在2，3两时刻的归一化距离为0.092 421，可以合并，所以得到2，3时刻的数据合并结果如图4（a）所示。接着，时刻（2， 3）与1 的归一化距离为0.088 093，可以合并；时刻（2， 3）与4 的归一化距离为0.159 589，不合并；最终得到的无法继续合并的结果即是化简后的质量矩阵，如图4（b）所示。该合并结果也与前文在例1中的分析相一致—1，2，3时刻1号数据源的质量情况比较相似，所以被合并在了一起，而0时刻和4时刻的状态与其它状态不同，所以被单独列出了。

图4 质量矩阵化简过程Fig.4 The reduction process of quality matrix

研究中需要注意的是，本文给出的质量矩阵及其化简框架中，质量度量函数Q和相似度度量函数Sim均是可替换的，可以根据应用场景来自由选择合适的质量度量函数Q和相似度度量函数Sim，在选择时只需保证2点，具体如下：

（1）质量度量函数Q应能够将dk中的每一个值映射为一个质量评分。

（2）相似度度量函数Sim应能够计算向量的相似度。

4 实验结果

用python对波兰城市克拉科夫的2017年的空气质量数据（天气、压强、温度、pm1、pm2.5、pm10）进行实验。其中，数据源为56个传感器，均对6个属性进行观测。实验数据包括自2017年1月1日到2017年12月24日的8 953条记录。

研究测试了所提出框架的效率和有效性。在效率方面，定制设计了2方面的实验。首先，保持阈值不变，测试随着时刻数目（原始质量矩阵行数）的增加，合并质量矩阵所需的时间变化，实验结果如图5所示。接着，保持时刻数目不变（固定在最大值），观察随着阈值的变化，合并所需的时间的变化，实验结果如图6所示。在有效性方面，保持时刻数目不变，观察阈值变化时矩阵大小的变化，实验结果如图7所示。

由图5可知，当固定阈值为0.1，同时不断增加时刻数目，测量对多个数据源的化简质量矩阵所需的平均时间变化。可以观察得知，该时间呈严格线性增加的变化趋势。

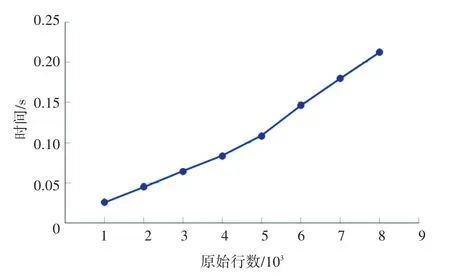
图5 原始行数对效率的影响Fig.5 The influence of original row numbers on efficiency

由图6可知，当固定原始数据行数为最大值，阈值从0～1变化时，测试合并时间的变化情况。分析结果可知，当阈值变化时，合并时间随阈值增大而增加，时间增加幅度却在递减。这是因为当阈值增大到一定程度（在本实验中约为0.4）之后，化简后的质量矩阵的大小基本不再发生大幅的变化，即每次化简合并的行数不再发生大的变化，故所需时间的变化也会较小。

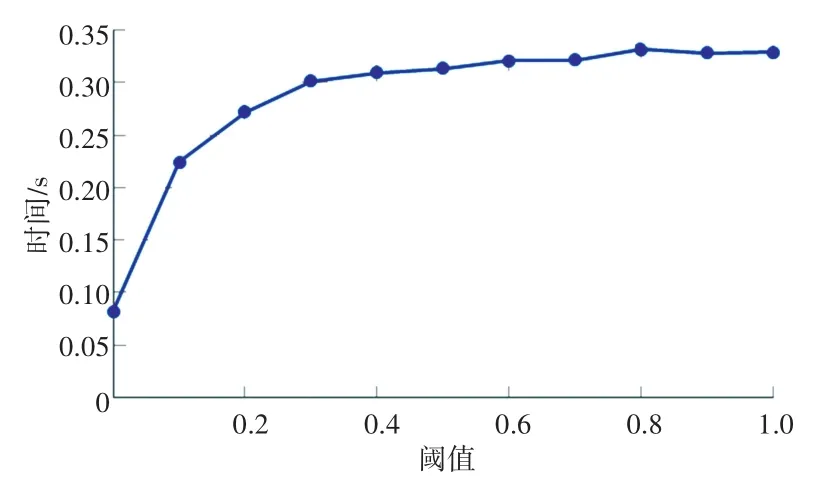
图6 阈值对效率的影响Fig.6 The influence of threshold on efficiency

由图7可知，当保持时刻数目不变时，测试阈值变化时化简后矩阵大小的变化。当阈值从0～1逐渐增大时，合并后的矩阵行数不断减少，减少幅度也随之逐渐变小。该实验结果也与图6中的实验结果互相印证，即当阈值增大到一定程度后，化简的结果将不再发生变化。因此在实际使用中，可以通过实验测定阈值和化简后矩阵的变化关系，大致给出阈值设定的建议，例如，可建议其将阈值设定在化简变化较陡的区域，这样只需要微调就可以看到结果的明显变化。

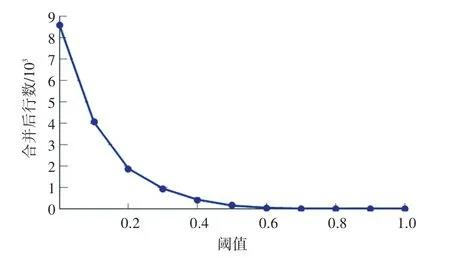
图7 阈值对化简后矩阵大小的影响Fig.7 The influence of threshold on reducted matrix size

5 结束语

针对目前传感器系统中的数据质量问题，本文提出了一种面向传感云的数据源质量评估框架。基于云端的大量历史数据，并借助云服务的计算能力，评估数据源的质量。本文定义了数据源质量矩阵，描述一个数据源在不同条件下的质量情况，给出质量矩阵的计算框架，从而快速高效地评估数据源的质量，确定哪些数据可被进一步应用于数据分析与查询。考虑到传感器网络中传感器数量多、环境复杂多变，可以获取的信息量巨大，在不同的数据质量状况下，如何从海量传感数据中，对数据质量和数据源质量进行不同角度的评估，仍是未来工作的重点。