水泥基材料渗透溶蚀有限元模拟方法
2019-05-15
(武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072)
1 研究背景
水泥基材料溶蚀是化学侵蚀的一类,根据水泥基材料所处的环境不同,可分为接触溶蚀和渗透溶蚀[1]。渗透溶蚀指水泥基材料在较高的渗透压强作用下,低碱度软水不断渗入,打破了水泥水化产物与孔隙液间的平衡,使可溶性水泥水化产物失去稳定性,并不断地向流动的孔隙液中水解、溶出、流失的全过程[2-3]。
在国内外的水利工程中,渗透溶蚀现象大量存在,如:美国的科罗拉多拱坝与鼓后池拱坝因溶蚀破坏而报废[4];印度的特赫里大坝的基础廊道壁面出现大量溶出石灰[5];我国的丰满、新安江、磨子潭等混凝土大坝也均存在不同程度的渗透溶蚀现象[6]。以丰满大坝为例,大坝的下游面及廊道表面曾出现大量白色和黄色的溶蚀物,坝体、坝基排水孔的孔壁溶出物大量沉积,坝体混凝土多年平均溶出量达9.6 t之多[7]。大量的室内溶蚀试验表明:在渗透溶蚀作用下,水泥水化物不断水解、溶出、流失,使得水泥基材料孔隙率与渗透性增大,水泥基材料强度降低[8-12]。因此,合理地描述工程在渗流条件下的渗透溶蚀空间分布、材料性能指标的演化,对工程结构安全性研究具有重要意义。
目前, 针对水泥基材料渗透溶蚀的问题, 国内学者做了大量的研究。 方坤河等[12]、 李新宇等[ 13]以提高混凝土耐久性为出发点, 针对水工碾压混凝土在软水环境下的渗透溶蚀开展了系统试验研究, 论述了影响混凝土抗渗透溶蚀性能的因素; 李金玉等进行了压力水下的混凝土渗漏溶蚀试验研究, 揭示了混凝土在渗漏溶蚀过程中的水泥水化产物、 孔隙结构及强度的变化规律[6]; 孔祥芝等[14]通过水工混凝土渗透溶蚀试验, 研究了水工混凝土的压力渗水规律及渗透溶蚀作用下混凝土性能衰减规律; 盛金昌等[10]针对不同配合比混凝土试样, 以地下水和碳酸溶液为渗透介质开展试验, 得出了溶蚀程度与混凝土配合比、粉煤灰掺量间的关系。
在以上对水泥基材料渗透溶蚀的研究中,均以室内试验开展,针对渗透溶蚀数值模拟方法的研究却鲜见报道。对此,本文针对水泥基材料渗透溶蚀的数值模拟方法开展研究,拟通过提出三维渗透溶蚀数学模型,采用有限元方法实现数值求解,建立渗透溶蚀的数值模拟方法,为水利工程中的渗透溶蚀数值模拟研究奠定基础。
2 渗透溶蚀数学模型
2.1 钙离子迁移数学模型
相关研究表明,水泥基材料溶蚀过程中溶出的主要是钙、硫、钾、铝等元素,其中,钙是决定水泥基材料力学性能的主要组成部分,因此,钙含量是反映水泥基材料性能退化的最好指标[15]。水泥基材料溶蚀过程中,离子迁移作用机理主要有水动力弥散、对流、物理吸附与解吸、内外电场作用等[16],其中起主导作用的是水动力弥散与对流作用[17]。本文基于离子在水泥基材料中的水动力弥散与对流作用机理,建立三维溶蚀过程中钙离子迁移数学模型,其假设条件为:①钙离子不发生吸附与解吸作用;②水泥基材料孔隙液流动为达西流,即遵循达西定律;③忽略温度对溶蚀进程的影响;④孔隙液中钙离子与骨架中的固相钙含量始终处于平衡状态;⑤水泥基材料中的渗流非饱和区不发生溶蚀。
2.1.1 钙离子迁移控制方程组
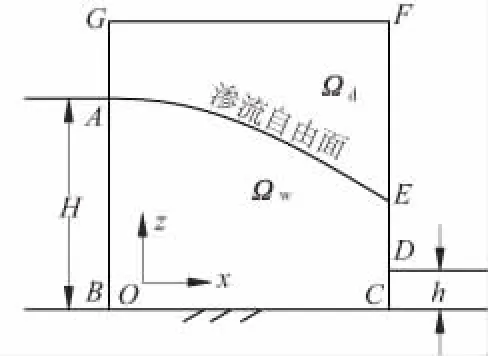
图1 模型边界示意图Fig.1 Schematic diagramof boundary conditions ofthe proposed model
为不失一般性,将以图1所示模型的渗透溶蚀问题为例,BCFG为水泥基材料块,BG侧和CF侧分别与环境水接触,BG侧水头为H,CF侧水头为h,在水头差的作用下,环境水渗入水泥基材料,AE为渗流自由面,ED为渗流溢出面,Ωd为干区,Ωw为湿区。根据钙离子质量守恒定律、Fick第二定律、多孔介质渗流控制方程、达西定律建立三维溶蚀过程中钙离子迁移控制建立方程组式(1),式(1)中第1个方程描述了钙离子在水泥基材料中的迁移,第2个方程描述了渗透介质在水泥基材料中的流动。
式中:φ为水泥基材料孔隙率;C为孔隙液中钙离子浓度;Dij(φ)为钙离子的有效扩散系数张量;Cs为固相钙含量;t为溶蚀时间;Kij(φ)为水泥基材料渗透系数张量;H为渗流场水头;Ss为单位贮存量;Vi为孔隙液通过断面的平均流速矢量,由达西定律式(2)计算得到,即
(2)
2.1.2 控制方程组求解条件
求解式(1)中的控制方程组,需给定如下所述初始条件与边界条件。
2.1.2.1 初始条件
初始条件有
(3)
2.1.2.2 钙离子迁移控制方程边界条件
(1) 定通量边界条件为
(4)
式中:q2为边界上已知钙离子的弥散通量;ni为边界的单位外法线方向余弦;Г代表边界区间。
(2) 离子交换边界条件[18-19]为
(5)
式中:kT为边界上孔隙液与环境水之间的传质系数;C0为环境水中钙离子浓度。
(3) 溢出面边界条件为
(6)
2.1.2.3 渗流控制方程边界条件
(1) 定水头边界条件为
(7)
式中:H1(x,y,z,t)在AB边界处取H,在CD边界处取h。
(2) 定通量边界条件为
(8)
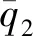
(3) 自由面边界条件为
(9)
式中:H*为自由面边界上的水头;Z为自由面边界的高程坐标。
(4) 溢出面边界条件为
(10)
式中:H为溢出面边界上的水头;Z为溢出面边界的高程坐标。
上述式(1)—式(10)即为水泥基材料渗透溶蚀过程中钙离子迁移数学模型。
2.2 固液平衡关系
钙离子迁移控制方程中含有固相钙浓度Cs与液相钙离子浓度C,相关研究表明,Cs与C两者具有一定的热动力平衡关系[20-21]。本文引用该固液平衡曲线得到C与Cs间的关系。固液平衡曲线如图2所示,关系式为
(11)
式中:x1为C-S-H凝胶(水化硅酸钙凝胶)开始快速溶解时孔隙液中的钙离子浓度;x2为Ca(OH)2完全溶解时孔隙液中的钙离子浓度;Csatu为孔隙液中钙离子饱和浓度;CCSH为水泥基材料中C-S-H凝胶的摩尔浓度;CCH为水泥基材料中Ca(OH)2的摩尔浓度。
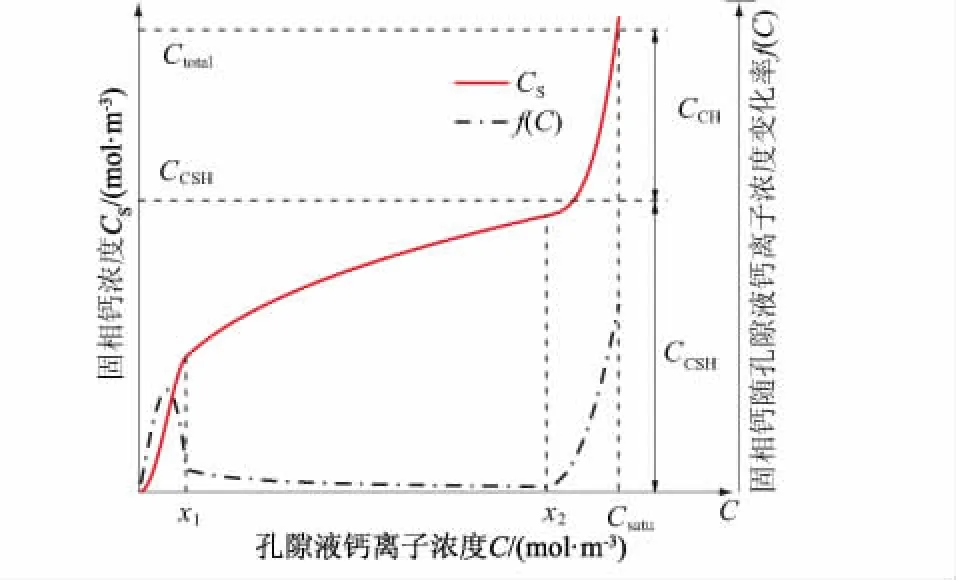
图2 固液平衡曲线Fig.2 Solid-liquid equilibrium curve
根据以上固液平衡关系,可将钙离子迁移控制方程组式(1)中的固相钙浓度转化为孔隙液中钙离子浓度,可得只含有水头与孔隙液中钙离子浓度2个变量的钙离子迁移控制方程组,即
(12)
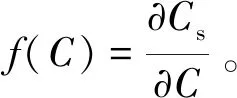
2.3 孔隙率演化模型
2.3.1 初始孔隙率计算
水泥基材料初始孔隙率可通过试验得到,也可通过计算获取,本文给出水泥基材料初始孔隙率计算方法。
水泥基材料内部孔隙分为毛细孔与凝胶孔,毛细孔与凝胶孔的体积率与水泥水化度密切相关。本文假设水泥基材料孔隙均匀分布,根据POWERS模型,水泥基材料初始孔隙率等于毛细孔隙率与凝胶孔隙率之和,即
(13)
式中:φcap为水泥浆毛细孔隙率;φgel为水泥浆凝胶孔隙率;φ0为水泥基材料初始孔隙率;α为水化度;W/C为水灰比;fC为水泥浆在水泥基材料中的体积分数。
水泥水化程度决定了水泥水化产物、水泥基材料的初始孔隙率,水化环境对水泥水化程度又有着极大的影响,水化度会随着环境的变化发生变化,其规律较为复杂。为简化模型,本文考虑材料的最大水化程度,即由于环境的限制,水泥水化无法继续时水泥的水化程度,采用式(14)计算[22-23]。
2.3.2 孔隙率演化
C-S-H凝胶与Ca(OH)2的溶解,造成水泥基材料的孔隙率增加,致使钙离子有效扩散系数与渗透系数增大,从而加剧水泥基材料的溶解。根据相关研究,孔隙率变化量可与水泥基材料中C-S-H凝胶与Ca(OH)2含量变化量建立关系,得到孔隙率演化模型。由于C-S-H凝胶溶解过程较为复杂,为了简化模型,本文假设C-S-H凝胶以Ca(OH)2形式溶解[22-24]。据此,可得到孔隙率与固相钙含量变化量间的关系,从而建立孔隙率演化模型,即
(15)
式中:φ0为初始孔隙率;Δφ为孔隙率变化率;ΔCs为固相钙含量变化量;MCH为Ca(OH)2的摩尔质量;ρCH为Ca(OH)2的密度;Cs0为初始固相钙含量。
2.4 扩散系数演化模型
随着孔隙率的变化,钙离子在水泥基材料中的扩散系数也会变化;另一方面,有效扩散系数与水泥基材料的骨料组成密切相关。参考相关研究[15, 25-26],通过引入孔隙的曲折度来考虑骨料对有效扩散系数的综合影响,本文建立如下的水泥基材料有效扩散系数演化通用模型,即
(16)
式中:D(φ)为水泥基材料中钙离子的有效扩散系数;D*(φ*)为水泥浆中钙离子的有效扩散系数;fp/m为水泥浆在砂浆中的体积分数;fm/c为砂浆在水泥基材料中的体积分数;φ*为水泥浆的孔隙率;τ为水泥基材料的孔隙曲折度。
3 有限元计算
3.1 空间离散
本文采用三维8节点等参单元对空间域进行离散,根据Galerkin方法原理,取试探函数为
(17)
式中:C代表空间域上任意一点孔隙液中钙离子浓度;Nm为等参单元的第m个节点形函数;Cm为等参单元的第m节点孔隙液中钙离子浓度;Hm为等参单元的第m个节点总水头。
由Galerkin方法可以得到
(18)
式中:Ωe为计算域Ω经空间离散后的单元体;Nn为等参单元的形函数。
对式(18)应用格林公式,经数学推导后,将边界条件、孔隙率演化模型代入后,整理可得
(19)
将式(17)代入式(19)后,整理可得
(20)
其中:
式中μ为渗流自由面变动范围的给水度。
3.2 时间离散
时间域离散方法有显式差分法、中心差分法、Galerkin权函数法、隐式差分法等方法,本文采用无条件稳定的隐式差分法离散时间域,即
(21)
式中:Ck+1与Ck分别为第k+1步和第k步的各节点浓度;Hk+1与Hk分别为第k+1步和第k步的各节点水头;Δt为时间迭代步长。
将式(21)代入式(20)可得隐式差分有限元迭代格式为
3.3 特殊处理
3.3.1 迭代格式处理
需要指出的是,方程组式(22)第一式左边[KC]与[DC]为稀疏对称矩阵,而[SC]为稀疏非对称矩阵。本文采用超松弛预处理共轭梯度法(SSOR-PCG)求解线性方程组。为提高求解效率,本文将[SC]矩阵移置方程右边,由此该方程左边系数矩阵变为稀疏对称矩阵。
3.3.2 协调质量矩阵处理
一般而言,时间步长较小时,求解精度较高,但笔者在计算过程中发现,当时间步长小于某一极限值时,数值解会在求解域内出现“阶跃现象”,相关研究表明,这是用有限元方法求解抛物型方程时必然面临的问题[27-28]。
通过数学逻辑推理[27]、数值试验[29]、物理意义[30]相关研究表明,在隐式差分法离散时间域的基础上,采用集中质量矩阵代替协调质量矩阵消除稳定的数值解对时间步长限制要求,进而消除“阶跃现象”。
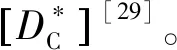
经过以上两类特殊处理后,隐式差分有限元迭代格式变为式(23),即
需要指出的是,方程组式(23)为耦合方程组。对于耦合方程组的求解有全耦合求解和半耦合求解2种方法,本文采用半耦合求解方法,即在一个迭代步内,先求解渗流场,再求解钙离子浓度场。
4 算 例
4.1 扩散系数模型的确定
4.1.1 水泥净浆扩散系数模型
水泥基材料的扩散系数演化模型需要选择水泥浆中钙离子有效扩散系数模型,目前,水泥浆中钙离子有效扩散系数计算模型有多种,本文采用由Mainguy等[31]根据试验数据提出的计算模型,即
D*(φ*)=D0ekφ*。
(24)
式中:D0取值为2.355×10-13m2/s;k取值为9.95。
4.1.2 孔隙曲折度计算模型
在计算混凝土一类的材料时,应考虑骨料对钙离子扩散的影响,因此需确定孔隙曲折度计算模型,本文算例中的孔隙曲折度由经验公式[15]计算,即
(25)
4.2 渗透溶蚀模拟
当水泥基材料在较高的渗透压强作用下,内部便会形成渗流场,此时材料产生渗透溶蚀。为验证模型及程序的正确性,本文引用文献[14]中的混凝土渗透溶蚀试验资料,进行数值模拟计算。
试件为圆柱体,尺寸为Φ430 mm×230 mm,采用42.5中热硅酸盐水泥,水泥化学成分及混凝土配合比详见文献[14]。渗透介质采用去离子水,采用逐级加压进行试验,加压过程如图3所示。
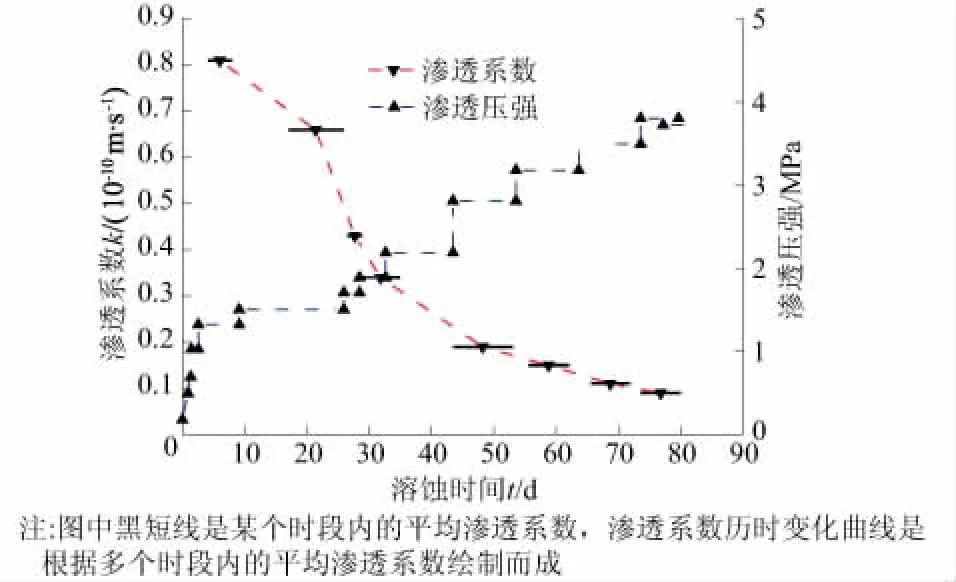
图3 渗透系数历时变化[14]Fig.3 Time histories of permeability coefficient andosmotic pressure[14]
渗透溶蚀过程中的固液平衡关系曲线参数取值如表1所示,模型计算其他参数如表2所示。
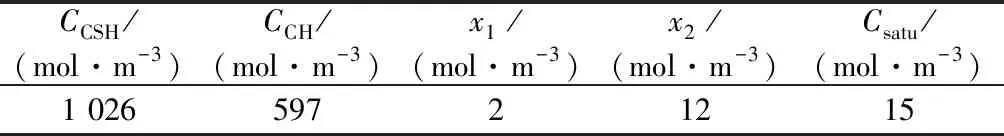
表1 固液平衡曲线基本参数Table 1 Basic parameters of solid-liquid equilibrium curve
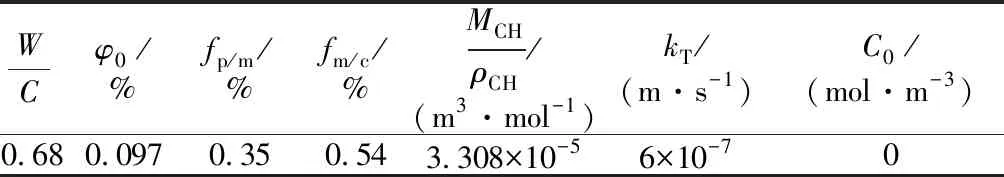
表2 模型计算基本输入参数Table 2 Basic input parameters of FEM program
注:kT取值参考文献[19]
基于本文所建立的渗透溶蚀模型,根据试验条件,可给出模型边界条件,如式(26)所示,相应的边界条件示意图如图4所示;另外,假设初始时刻,混凝土试块的孔隙中充满孔隙液,且孔隙液中钙离子浓度为饱和浓度。
(26)
图4 渗流场与浓度场边界条件示意图Fig.4 Schematic diagram of the boundary conditionsof seepage filed and concentration filed
需要指出的是,混凝土的渗透系数与孔隙率相关,但两者并不是简单的函数关系,其渗透性高低取决于混凝土的孔隙结构特征[3]。一方面考虑到文献[14]中渗透溶蚀试验时间较短,渗透溶蚀引起的孔隙率变化较小;另一方面,由于去离子水渗入混凝土内部,混凝土发生二次水化,使得混凝土渗透系数不断降低;因此本算例忽略混凝土渗透溶蚀过程中孔隙率变化对渗透系数的影响,为得到更准确的渗透系数,本算例中的渗透系数通过文献[14]中渗透溶蚀试验实测数据线性插值获取,实测渗透系数如图3所示。
考虑到试验前期通过混凝土的渗流尚未完全贯通, 因此本文从第10天开始模拟计算,Ca2+累计溶出量从第10天开始累计。 图5为计算结果与文献[14]中相关的渗透溶蚀试验数据对比结果,通过对比可知,本文提出的模型计算结果与试验数据具有较好的一致性,进一步证明了本文提出的模型及程序的正确性。需要指出的是,虽然试件的渗透系数在不断减小,但试件下边界的孔隙液中钙离子浓度却始终保持不变,因此Ca2+累计溶出量与渗流量成正比,如图5(b)所示,该结果与渗透溶蚀作用下的钙离子溶出第一阶段的特征相符[2]。
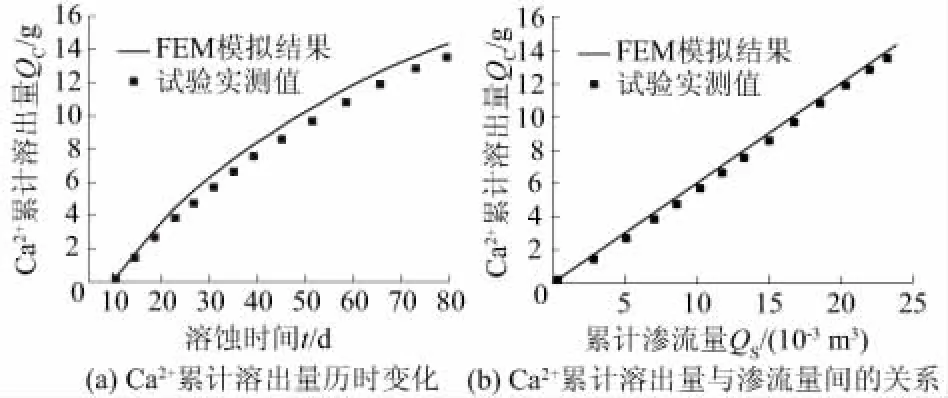
图5 Ca2+累计溶出量与试验数据[14]对比Fig.5 Comparison of cumulative calcium leachingbetween model result and experimental result inReference[14]
5 结 论
(1)根据钙离子迁移数学模型、固液平衡关系、孔隙率演化模型、扩散系数演化模型建立了水泥基材料的渗透溶蚀数学模型,给出该数学模型的有限元计算方法。
(2)针对渗透溶蚀过程开展数值模拟,模拟所得到的Ca2+累计溶出量与文献试验数据基本吻合。数值验证表明:本文建立的渗透溶蚀模型能够用于模拟水泥基材料的渗透溶蚀过程;通过有限元计算方法可以定量地计算三维渗透溶蚀过程中水泥基材料的固相钙溶出量。
