一种基于土体率敏性的长期变形预测方法
2019-05-15王智超1郑军星
王智超1,,胡 茜,郑军星,熊 赟
(1. 湘潭大学 岩土力学与工程安全湖南省重点实验室培育基地,湖南 湘潭 411105;2.湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
1 研究背景
近年来随着我国经济的迅猛发展和城市化进程的快速推进,大量基础设施(如道路桥梁、地下工程、水利设施、海防、堤坝工程以及港口工程等)不断涌现,其地基土长期沉降变形的预测与控制往往成为这些工程建设的关键性问题。早在20世纪50年代,蠕变就受到诸多学者的广泛关注,工程实践经验和理论分析逐渐受到重视,形成了诸多构筑物沉降理论[1-3]。然而,传统的结合蠕变试验来预测土体变形的方法存在耗时长、难以考虑复杂应力路径以及不便用于复杂有限元计算分析等缺点。土体除蠕变外,还具有较为显著的率敏性,它表现为其受荷响应与加载速率密切相关的现象。Buisman (1936)[4]已经意识到土体应力-应变关系具有率相关性,并影响着实际岩土工程的变形与稳定,造成诸如失稳或长期沉降等工程问题。Leroueil等[5]针对大量一维加载速率试验结果,认为黏土的一维强度与加载速率具有一一对应的关系;一维固结CRS试验表明,加载速率越大,黏土的先期固结压力Pc就越大。Adachi等[6]通过对土的CRS三轴剪切加载试验发现应变速率与土的当前动屈服应力近似存在双对数关系。陈铁林等[7]对人工制备结构性黏土和重塑土开展了不同速率下的三轴试验,发现黏土在加载速率影响下,具有应变速率软化现象,即应变软化特性在高应变速率下更为明显。但汉波等[8]认为K0固结软土强度参量的率敏性与次固结系数和压缩指数等压缩参数有关。吕宾林等[9]则认为在CU三轴试验中,固结压力越大,黏土的黏聚力、内摩擦角以及不排水抗剪强度率敏性越明显。可见,土体率敏性也是土体时间相依的重要变形特征。基于此,本文拟结合土体的率敏性特征,通过对饱和超固结土以及人工制备结构性土分别开展3种不同加载速率下的三轴剪切试验,获得土体强度、变形以及率敏性指标;从而得到了基于上下负荷面的弹黏塑性本构模型参数,并利用该模型来预测土体的率敏性和蠕变变形行为;最后通过2种土体的蠕变试验结果来对模型预测结果进行检验。
2 土体率敏性试验
为揭示率敏性对黏土应力-应变规律的影响,进而确定弹黏塑性本构模型中的率敏性参数,本文开展了饱和重塑超固结土和人工制备结构性土率敏性三轴试验。
2.1 2种土类率敏性试验方案
饱和超固结土和人工制备结构性土都采用不排水三轴剪切试验。超固结土采用0.562 5,0.037 5,0.002 5%/min 3个速率分别加载,超固结比OCR分别为1,2,4,8,16。为模拟高应力历史、重超固结工况,试样均在800 kPa有效围压下等向固结,采用固结-加载-回弹的模式获得超固结比OCR=16,8,4,2的试样,其中试样在试验过程中设定反压400 kPa。人工制备结构性土具有大孔隙和颗粒间胶结作用等特征,试验将原料土、高岭土、水泥和国产大颗粒食盐碾碎过0.5 mm的筛备用,配置大小为Φ39.1 mm×80 mm、水泥含量6%、孔隙比1.6的标准三轴试样。试样抽真空后在恒温水浴中养护6 d,通过水的循环流动把试样中的盐完全溶解而产生孔隙,从而控制孔隙比,采用1.000,0.070,0.007 mm/min 3个速率分别加载。2种试验的所有试样在剪切压缩前都对试样进行孔隙水压力系数B值检测,结果显示饱和度均>98%,表明试样达到充分饱和。
2.2 试验结果
图1为正常固结和超固结下应力-应变曲线。从图1中可以看出,饱和超固结重塑土的率敏性较为明显,不同超固结状态下,不排水抗剪强度均随加载速率的升高而不同程度增大。
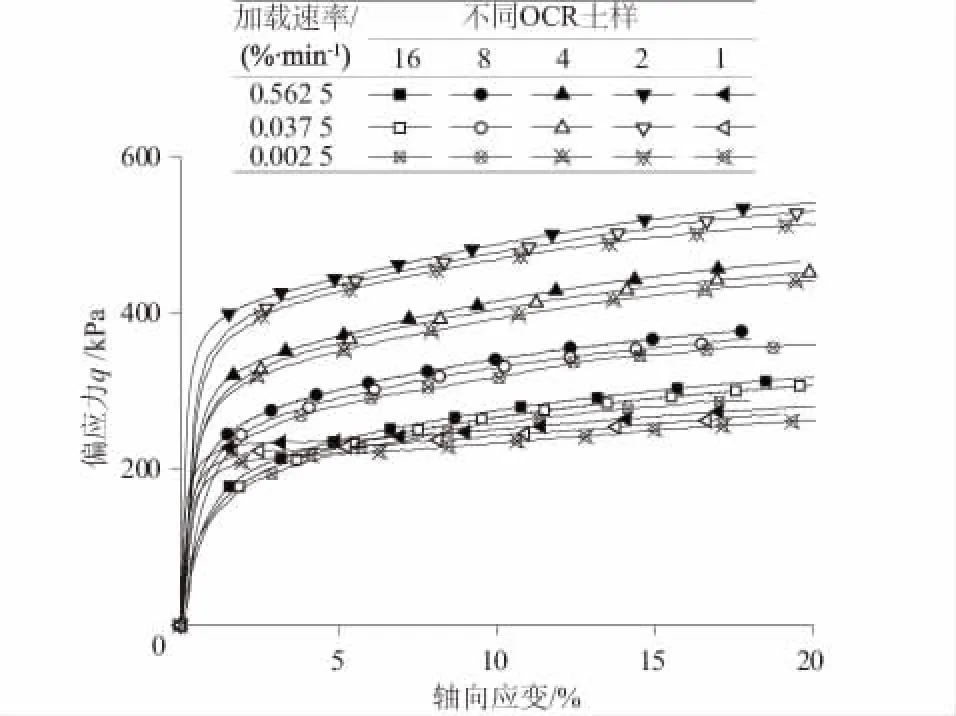
图1 饱和超固结土应力-应变曲线Fig.1 Stress-strain curves of saturated remouldedover-consolidated clay
图2是人工制备结构性土在不同试验围压条件下的应力-应变曲线。 从图2可以看出, 结构性土在不同试验围压条件下, 高应变速率均发生应变软化现象, 同一围压条件下高应变速率下的软化特性比低应变速率下的软化特性明显, 且不同的应变速率对试样强度有一定的影响, 具有一定的率敏性。
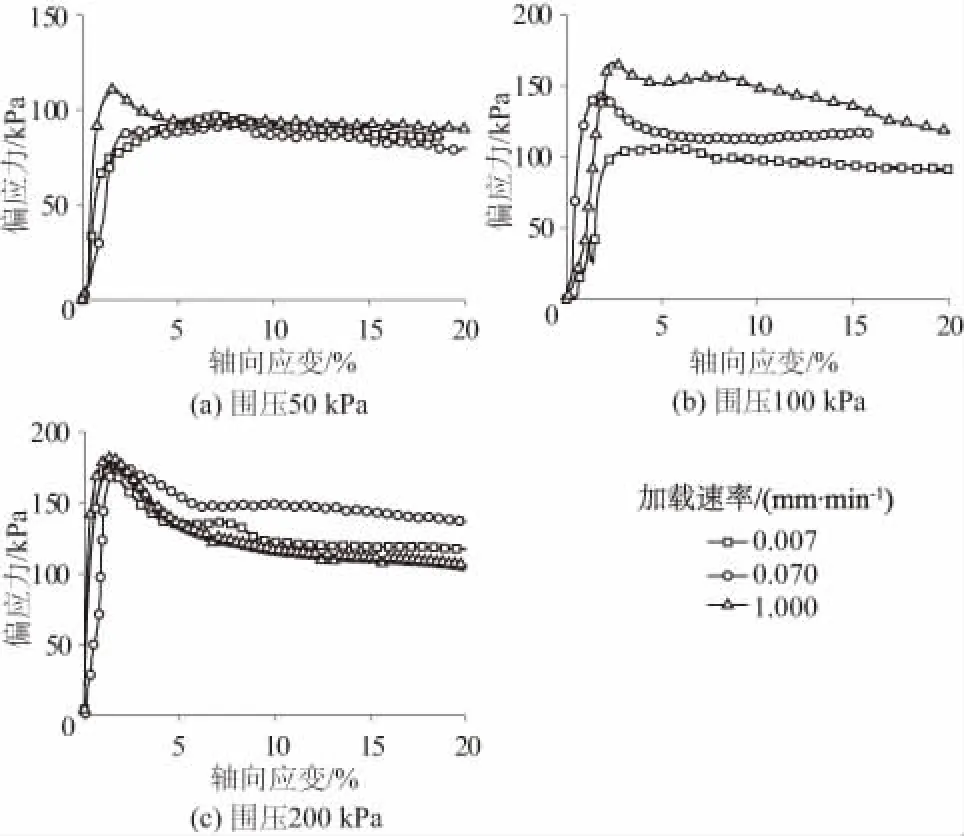
图2 人工制备结构性土应力-应变曲线Fig.2 Stress-strain curves of artificial structural clay
3 基于上下负荷面的弹黏塑性本构模型
3.1 基本理论
目前,与土宏观时效本构理论相关的试验主要有率敏性试验和蠕变试验,结合以上2类土体的流变试验和Perzyna[10]的过应力理论,奠定土体弹黏塑性本构模型建立的基础,基于前者建立的模型称之为率敏性模型,基于后者的称之为蠕变型模型。Freitas等[11]通过对这2类模型三轴剪切数值模拟试验数据对比分析指出,在应力水平<0.6时,2类模型的预测差异较小,但在高应力水平时蠕变型模型预测的结果误差较大,因此采用率敏性试验为基础建立弹黏塑性本构模型,再辅以蠕变试验对模型进行校验将更为合理,即为本文的研究思路。为了表征不同应变速率对土体力学性质的影响,本文引用了王智超等[12]基于上下负荷面理论提出的一类可表征饱和超固结土以及结构性土的弹黏塑性本构模型。如图3所示,为了正确描述土的超固结特性、结构特性及率敏性,分别引入当前动屈服面fd、参考下负荷面fu[13]、参考正常固结屈服面fs(Roscoe,1963)及参考上负荷面fw[14]。令通过A,B,C3点的3个参考屈服面几何相似,则
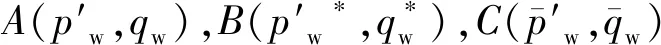
(2)
式中:初始R的倒数定义为超固结比,记为ω(ω≥1);初始R*定义为结构性参数(或称灵敏系数),记为ζ(0<ζ≤1)。当ζ=1时,表明土体无结构性,且随着ζ的减少,土体的结构性逐步增强。
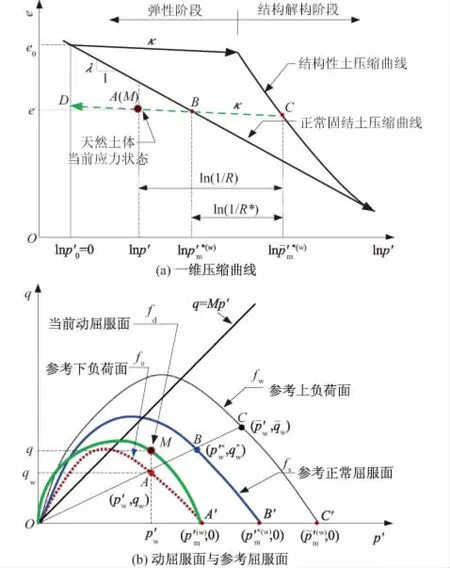
图3 基于上下负荷面的相对过应力关系[12]Fig.3 Elasto-viscoplastic constitutive model ofstructured clay based on a relative overstress relation[12]
(3)
式中:fd为动屈服面;σij为应力分量;相对过应力函数〈Φ(F)〉定义为
(4)
式中:c0为率敏性系数;m′为过应力系数;c0和m′均可通过不同应变速率三轴压缩试验测定;kd和ku分别是动屈服面的硬化参数和参考屈服面的体积硬化参数。
借助相对过应力思路,以上下负荷面为参考屈服面,则可得到结构性软土的动屈服准则函数为
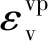
(6)
式中α和β分别为控制R和R*的演化速率参数。
3.2 模型参数
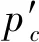
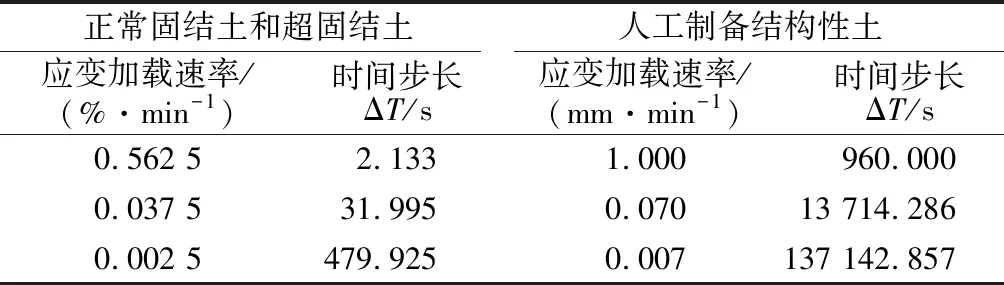
表1 3种应变速率对应的时间步长Table 1 Time steps of three strain rates

表2 本构模型参数Table 2 Parameters of constitutive model
3.3 土体率敏性的变形表征预测
3.3.1 正常固结土率敏性变形预测
正常固结黏土在400 kPa围压和3种加载速率下的应力-应变关系预测如图4所示。需要指出的是,土体在固结过程中可能会产生轻微老化,因此模型输入的超固结比设为1.2(保证应力历史不变,降低加载围压)。可以看出,模型预测结果在弹塑性阶段具有轻微向上倾斜的趋势,和试验结果相近,另外模型也能合理地模拟不同加载速率的变形情况,说明模型能够较为准确地表征正常固结土的率敏性变形特征。
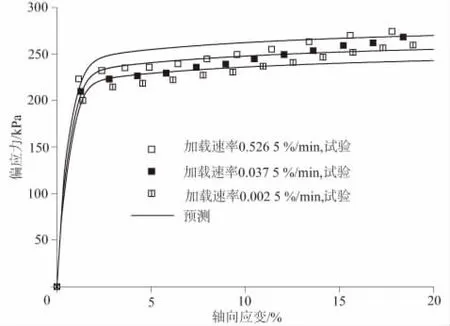
图4 正常固结黏土率敏性变形预测Fig.4 Deformation prediction for normally consolidatedclay based on rate sensitivity
3.3.2 超固结土率敏性变形预测
几类超固结土在3种加载速率下的应力-应变曲线如图5所示,对比试验曲线和模型预测曲线的变形特征,本文提出的基于上下负荷面的弹黏塑性本构模型能够合理地表征超固结土的强度特性和率敏性,对于两者的耦合作用效果预测较好。

图5 超固结黏土率敏性变形预测结果Fig.5 Deformation prediction for over-consolidatedclay based on rate sensitivity
3.3.3 结构性土率敏性试验预测
人工制备结构性土在100 kPa围压和3种加载速率下的应力-应变关系预测如图6所示,由图6可以看出,模型预测结果和试验结果均发生应变软化现象,两者峰值强度相差不大,当轴向应变达到10%以后,两者变化趋势基本一致,这说明该模型对其耦合作用效果预测较好,能够较为准确地表征人工制备结构性土的率敏性变形特征。
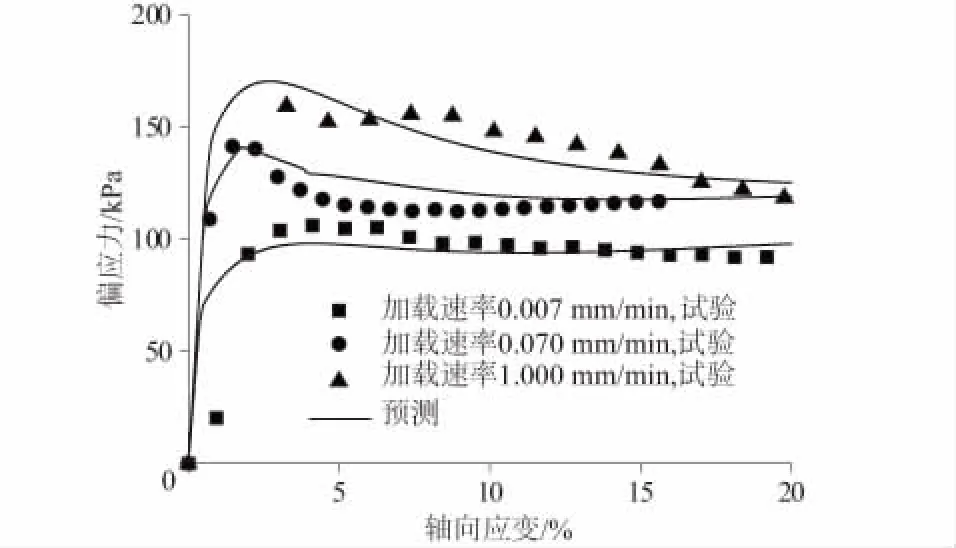
图6 人工制备结构性土率敏性变形预测Fig.6 Deformation prediction for artificial structuralclay based on rate sensitivity

图7 超固结土蠕变试验及模型预测结果Fig.7 Results of creep test and model forecasts forover-consolidated clay
4 土体蠕变特性验证
为了更好地对土体长期沉降变形进行预测,进一步验证模型的合理性,本文分别对饱和超固结土和人工制备结构性土开展了三轴剪切蠕变试验,以验证模型的准确性。试验采用前文土体率敏性试验的方法获取不同超固结状态的超固结土(OCR分别为8和16)和孔隙比1.6、水泥含量6%的人工制备结构性土,根据已整理的应力-应变规律,以某一黏塑性变形阶段的应力状态作为偏应力,开展了蠕变试验,偏应力的施加方式采用分别加载(瞬时加载)。
4.1 超固结土蠕变特性验证
图7为2类超固结土(OCR=16和OCR=8)的三轴剪切蠕变试验结果及模型预测结果,模型参数输入同预测饱和超固结土率敏性的模型参数一致,2类超固结土的偏应力设定为试验中施加的偏应力。
从图7中可以看出,提出的模型能够合理地预测超固结土的蠕变特性,尤其在3 000 min以后预测误差较小。另外,新模型同样能够预测不同应力水平下超固结土的蠕变特性,且随着偏应力的减小,最终的轴向应变减小。
4.2 人工制备结构性土蠕变特性验证
图8为人工制备结构性土(孔隙比1.6、水泥含量6%)试样的三轴剪切蠕变试验结果和模型预测结果。可以看出,蠕变试验曲线与预测曲线趋势基本保持一致,提出的弹黏塑性本构模型能够合理预测结构性土的蠕变特性。
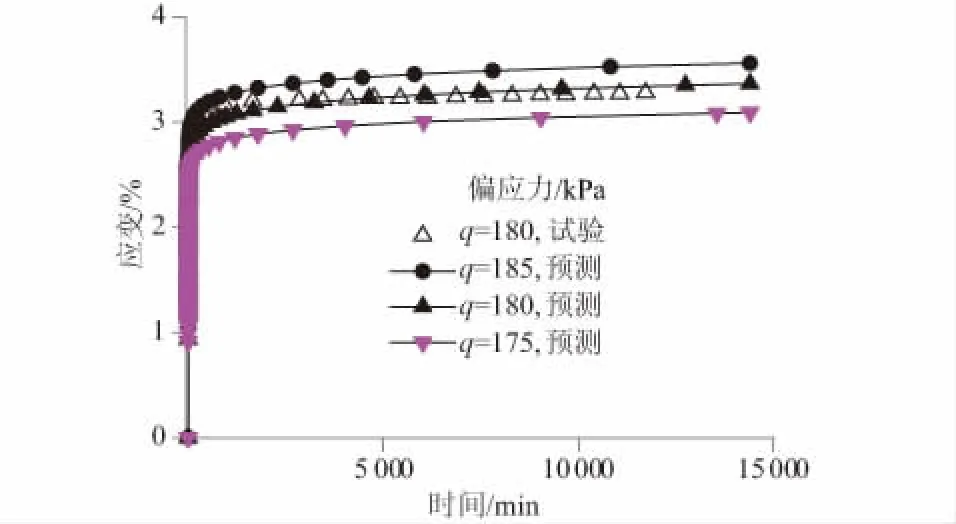
图8 人工制备结构性土蠕变试验及模型预测结果Fig.8 Results of creep test and model forecasts forartificial structural clay
5 结 语
本文通过对饱和超固结土和人工制备结构性土开展不同加载速率的三轴压缩率敏性试验,并以该试验确定弹黏塑性本构模型参数,预测土体的蠕变变形,研究表明:
(1)饱和超固结土和人工制备结构性土都具有明显的率敏性。
(2)通过率敏性试验确定的基于上下负荷面的弹黏塑性本构模型参数,能成功用于预测土体的率敏性和蠕变变形行为。
(3)本研究为土体沉降计算与预测提供了一种较为便捷和准确的新方法。
