基于粒子群算法的微电网电动汽车接入经济-环境效益分析

王守文 宋林洁 周卫华

(1.三峡大学 法学与公共管理学院，湖北 宜昌 443002； 2.华中科技大学 经济学院，武汉 430074； 3.三峡大学 电气与新能源学院，湖北 宜昌 443002； 4.三峡大学 社会科学处，湖北 宜昌 443002)

微电网快速发展改变了能源消费现状，在交通方式上也逐渐得到体现，安全可靠、灵活经济、高效节能的微电网与绿色、环保、低噪音的电动汽车正逐渐受到社会各界的关注[1]．

目前，国内外学者主要从电动汽车接入对微电网的影响、电动汽车参与的微电网优化调度以及电动汽车接入微电网模式3个方面进行了研究．在对微电网影响方面，苏小林等[2]从过负荷和谐波方面分析了电动汽车的大规模充电对电能质量的影响．在优化调度方面，毛玉荣[3]以微电网新能源利用率最大为目标，提出了一种两阶段调度模型．在电动汽车接入微电网模式的研究上，查理[4]认为通过可适应充电方式，能够降低电网负担并满足用户需求；邵艾博[5]在采用负荷平衡及规划机制后，总能量消耗减少，同时电动汽车消耗的能量没有发生变化．

现阶段对电动汽车与微电网独立发展的研究已足够成熟，但大规模EV(Electric Vehicle)接入微电网的研究还不成体系．因此，灵活控制电动汽车在电力负荷和电储设备两种角色之间的转换，与微电网中其他能量单元实现协调运行，才能进一步降低微电网规划总成本，带来经济效益[1]和环境效益[6]．为更好地协调微电网中风力发电、光伏发电、微型燃气轮机发电等分布式能源与电动汽车(EV)的发展，本文利用蒙特卡洛算法仿真出未来一天大规模电动汽车充电行为规律；并在此基础上建立了能够同时考虑经济、环境成本的微电网多目标优化模型，将多目标函数简化为单目标模型以简化运算；最后通过实证分析验证了模型的正确可靠性．

1 电动汽车接入微电网运行模式

在先进的能量管理装置与科学的峰谷分时电价的协调管理下，电动汽车用户通过换电站进行有序充放电，微电网通过消纳分布式能源以供普通负荷以及电动汽车用户使用，并通过换电站和PCC开关协调实现电能的余量上网、余缺网补，大电网可以通过换电站和PCC开关在负荷高峰时段向微电网或换电站购入电能，在负荷低谷时段售出电能，满足电网的经济性，并达到削峰填谷的目的．电动汽车接入微电网的运行模式如图1所示．

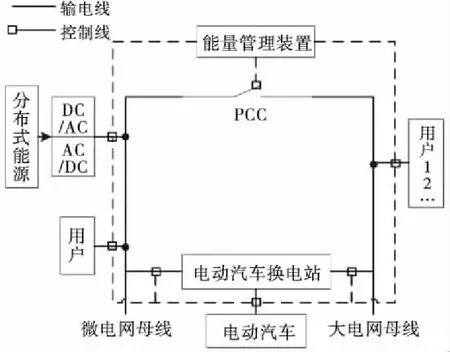
图1 电动汽车接入微电网运行模式

2 计入电动汽车的微电网优化模型构建

2.1 风机出力模型

风机发电功率计算公式如下[7]：

(1)

其中，P(v)为风机出力功率；Pr为风机额定输出功率；v为实际风速(m/s)；vi为风机切入风速；vr为额定风速；vc为截止风速；fP(v)为输出特性．

其中输出特性公式，即风速功率关系，服从幂函数计算公式：

fP(v)=a(v-vi)b

(2)

并由拟合结果得：a=61.06，b=1.173．

2.2 光伏阵列功率模型

光伏阵列的功率输出模型如下[8]：

(3)

其中，PPV为光伏阵列出力功率；fPV为降额因数；YPV为光伏阵列容量(kW)；IT为地表面实测光照度(kW/m2)；IS为标准光照度；αP为功率温度系数；Tcell为当前光伏电池表面温度(℃)；Tcell,stc为标准温度，一般取25℃．

2.3 微型燃气轮机模型

微型燃气轮机有功出力与热出力关系模型如下：

(4)

其中，PMT，QMT分别为微型燃气轮机的有功出力与热出力；ηe，ηt分别为发电、发热效率系数．

(5)

其中，VMT为微型燃气轮机燃料消耗量；qLH，gas为燃料低热值(kW·h/m3)；Δt为单位时间间隔，取1 h．

(6)

其中，kMT为微型燃气轮机的热电效率比；a，b，c均为常系数[9]．

2.4 电动汽车充电特性模型

对于某一地区，电动汽车保有量是确定值，假设常规充电的电动汽车电池容量、电动汽车平均充电功率及每公里平均耗电量为固定值，数据见表1，且无充电时长的限制．对电动汽车充电行为的3个特征量(充电开始时刻、连接时长和充电电量)与电动汽车平均充电功率构建规模电动汽车充电特性模型如下：

(7)

其中，SC为总充电电量；N为接入微电网的电动汽车数量；t0为充电开始时刻；TC为连接时长；PC(t)为平均充电功率．

表1 电动汽车相关参数

在平均充电功率下，充电连接时长满足下式：

(8)

其中，Si为电池容量；d为日行驶里程；W为每公里平均耗电量．

2.5 微电网系统成本模型

构建计入电动汽车的微电网经济-环境效益优化模型的目标函数如下：

Ctotal=min(CF，CQ，CM，CEV)

(9)

式中，Ctotal为微电网与电动汽车系统总成本；CF为微电网各设备初始投建成本；CQ为系统运维成本；CM为CO2、SO2、NOX等气体排放的环境总成本；CEV为电动汽车并网费用．

构建单目标微电网系统成本函数模型如下：

minCtotal=m1CF+m2CQ+m3CM+m4CEV

(10)

式中，m1，m2，m3，m4为各指标的综合权重．

1)微电网风力发电机组、光伏阵列以及微型燃气轮机各设备初始投建成本CF：

CF=CWT+CPV+CMT

(11)

式中，CWT、CPV、CMT分别为风力发电、光伏发电、微型燃气轮机各设备的初始投建成本．

2)微电网运维成本CQ包括风力发电、光伏发电、微型燃气轮机的日常维护费用和燃气轮机的燃料费用．微电网机组出力以及电动汽车充放电过程均存 在损耗，效率约为92%[10]，公式如下：

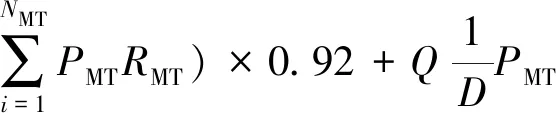
(12)

式中，Pi为第i种机组电源的出力；RWT、RPV、RMT分别为3种分布式电源的日常维护费用；Q为天然气价格；D为天然气低热值．

3)CO2、SO2、NOX等气体排放的环境总成本CM：

CM=k1M1+k2M2+k3M3

(13)

式中，k1、k2、k3分别为CO2、SO2、NOX等气体对大气的危害程度，M1、M2、M3分别为3种污染气体的排放量．

4)电动汽车不会有污染气体的排放，其燃料来源于微电网的清洁能源发电，因此电动汽车的并网费用包括电动汽车初始投资成本，以及电动汽车向微电网购电费用，公式如下：

(14)

式中，C1为电动汽车购置费用；SC(t)为单位时间内电动汽车总充电电量；RC(t)表示在t时段用户电动汽车向系统售电电价；RD(t)表示在t时段向系统的购电电价．其中约束条件为

(15)

式中，P1为微电网从低压配电网吸收的有功功率；PEV为电动汽车充放电功率，正值表示充电，负值表示放电；PL为微电网负荷；Pc，min，Pc，max分别为微电源充电下限和上限；Pd，min，Pd，max分别为微电源放电下限和上限．

3 微电网电动汽车接入效益的实证分析

3.1 电动汽车接入微电网负荷曲线预测

利用蒙特卡罗算法抽取电动汽车起始SOC，在满足充电所需时长和已给充电起始时间的限制下，进行负荷量的计算．以某地100辆电动汽车为例，利用蒙特卡罗算法抽取起始SOC，在满足充电所需时长和已给充电起始时间的限制下，进行负荷量的计算，通过100辆电动汽车的时间与开始充电时刻、充电连接时长、充电电量等相关数据导入可以仿真出大规模电动汽车充电行为符合正态分布(如图2所示)．

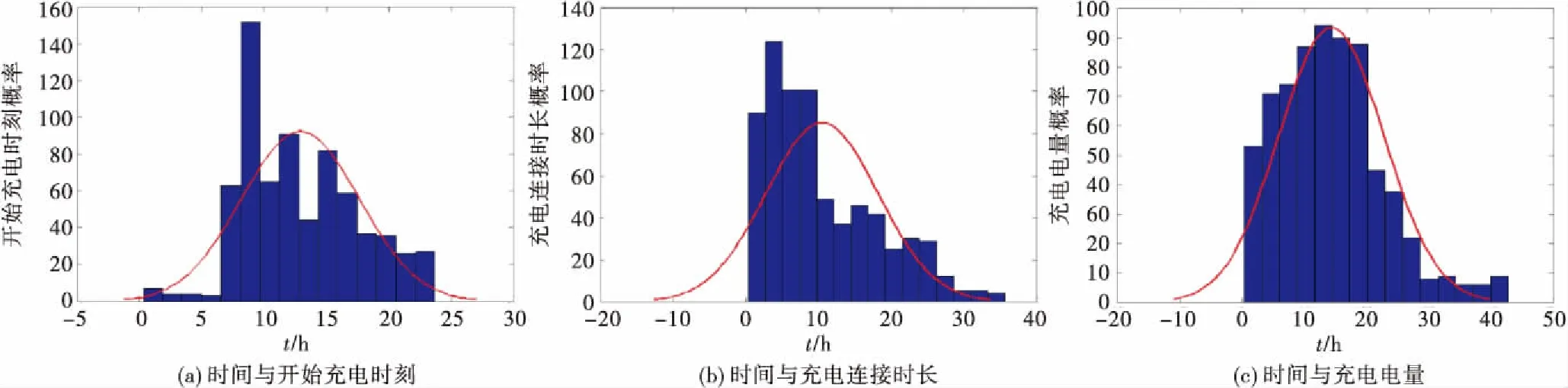
图2 大规模电动汽车充电行为特征量概率分布图

由上得出电动汽车充电行为特征量的分布规律后，计算100辆电动汽车的充电负荷规律，并计算得到未来一天规模化EVs总体负荷曲线与微电网发电量进行对比得到图3；通过分析曲线特征，可以看到微电网发电电量存在不满足用户需求电量的问题，在不满足用户需求时会产生向大电网购电的一系列行为，也可以为下一步预测出规模化EVs有序充电的最优系统成本提供数据支持[11]．

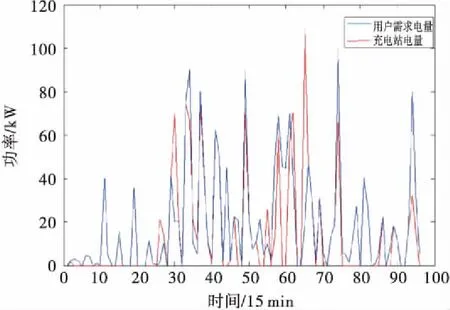
图3 预测未来一天规模化EVs总体负荷曲线与微电网发电量

3.2 电动汽车接入微电网最优系统成本

模型主要技术参数如下．

风机参数：风机额定输出功率850 kW；风机切入风速4 m/s；额定风速13 m/s；截止风速25 m/s．

光伏阵列参数：降额因数0.9；标准光照度取1 kW/m2，功率温度系数取-0.5%/℃．

微型燃气轮机参数：热功率取228 kW，微型燃气轮机的热电效率比取50%，燃料低热值取9.77 kW·h/m3．

POS参数：c1=c2=1.494，w=0.729，最大迭代次数Tmax=170，粒子数选取100．并与不计及电动汽车的微电网系统成本进行对比．

分析所需机组投运成本见表2[12]．

表2 机组投运成本

污染物参数见表3．

表3 污染物参数

以某地微电网购电电价为依据见表4．

表4 某地微电网各时段购电电价

1)AHP对各因素的重要性进行两两比较．

在假设各指标相互独立的前提下，为了使数据更加标准合理化，设计调查问卷并邀请50位本领域专家(包括高校电力学科研究人员、国家电网和南方电网等电网公司的技术人员、电力销售部门高层等)组成专家小组，对小组成员进行逐一采访并开展讨论得到最初的判断矩阵，判断矩阵通过了一致性检验可得到初始权重，再将影响度加权到初始权重中得到综合矩阵(见表5)．

表5 成本系数评估总权重

2)基于迭代的优化技术粒子算法．

在170次迭代中取9次最优结果得到迭代收敛结果，如图4所示．其中实线部分为不计电动汽车并网情况下的系统成本；虚线部分为计入电动汽车并网情况下系统成本．对算例进行两次仿真，第一次为不计入电动汽车的微电网运行模式，第二次在其他条件不变的情况下在微电网运行模式下接入电动汽车，得到两条系统总成本曲线(如图4所示)．一方面，在170次迭代中，随着迭代的次数增加系统成本也呈现出递减的趋势，并且系统成本能够跳出局部最优，进而在全局内完成寻优过程得到系统成本最低值．另一方面，计入电动汽车的微电网系统在第122次迭代时系统总成本收敛到890万元，不计入电动汽车其迭代次数在114次时系统总成本收敛于980万元．算例分析结果表明，虽然计入电动汽车的目标函数的迭代次数比只计微电网系统的迭代次数多1次，但系统总成本却有明显的降低．

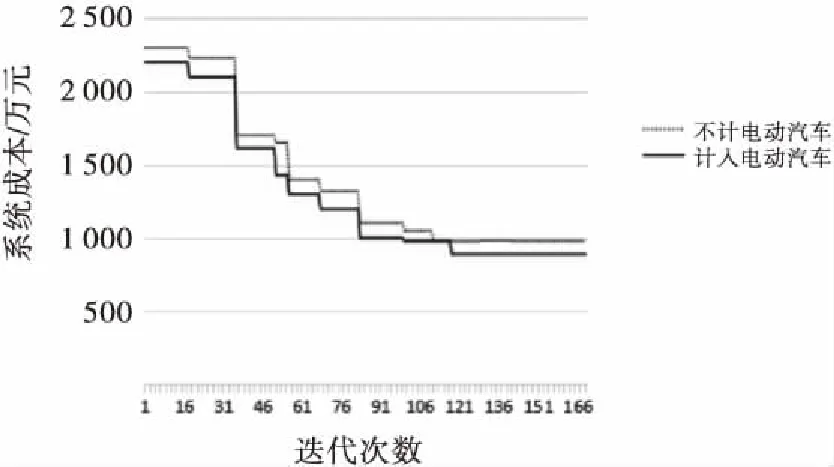
图4 迭代收敛图

3)微电网各单元最优出力情况．

将算例带入Matlab中得到包含EVs与不包含EVs的两种情况的微电网各单元最优出力，见表6．

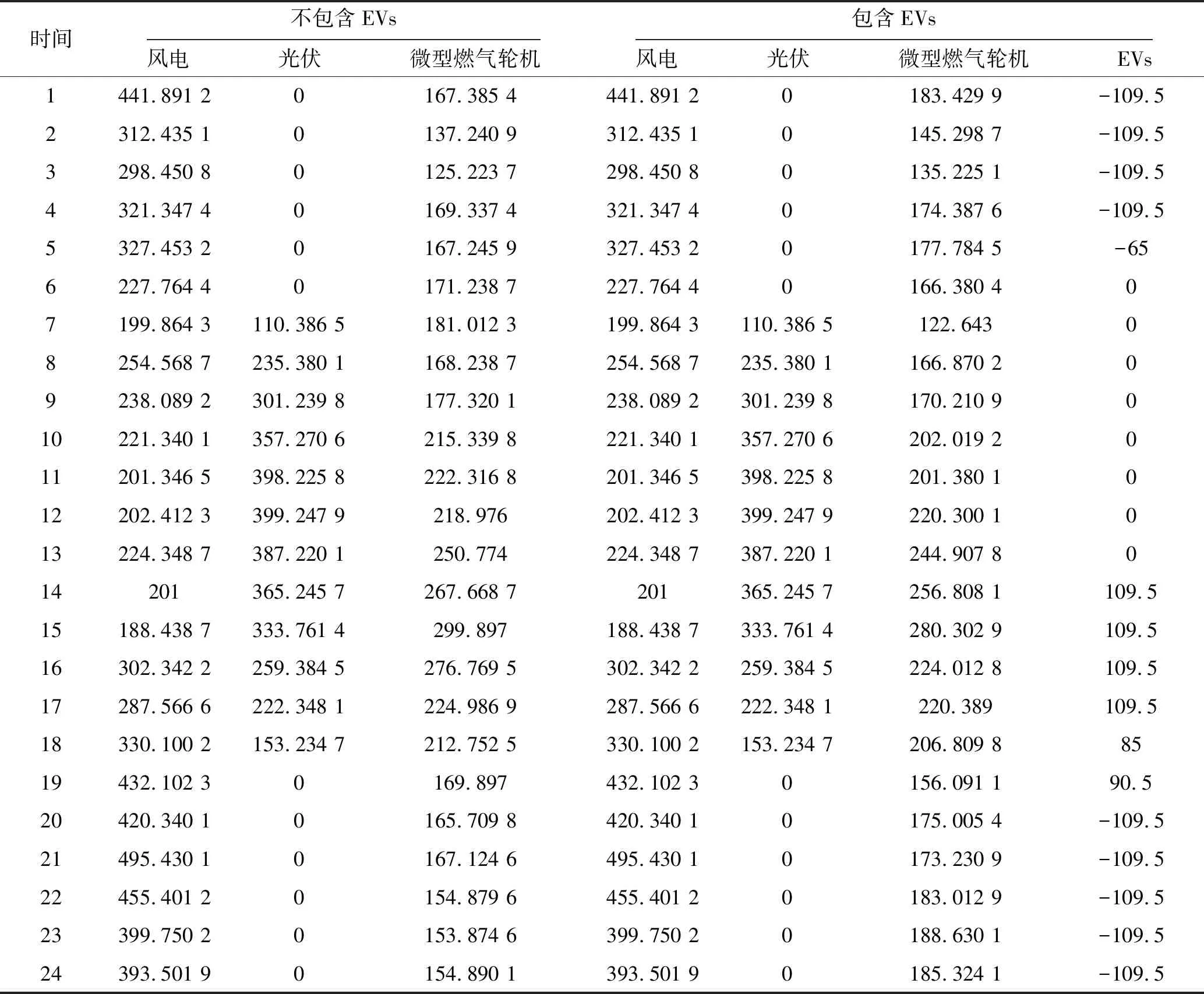
表6 微电网各单元最优出力 (单位：kV)

如表6所示为未来24 h不包含EVs微电网各单元最优出力和包含电动汽车微电网各单元最优出力，假设微电网发电设备与储能设备都是偏紧配置，即在负荷高峰期，在各发电单元提供的电能外(其中，风电与光伏发电为不可控发电设备，微型燃气轮机为可控发电设备)，由可调度电动汽车进行电能补充，最后再考虑向大电网购电．可以看到负荷高峰期集中在10：00-18:00之间，但由于风力发电的反调峰特征，使得微型燃气轮机的输出处于高峰期．在平谷期，风能和太阳能较为充足，微型燃气轮机输出较少．横向对比，包含与不包含EVs的微电网中可以看到可调度的电动汽车相当于一个没有投资成本的移动蓄电池，因此，大规模电动汽车的并入可以起到降低微电网系统成本的作用．另外，给用户也带来了可观的收益，达到了双赢的效果．

4 结 论

本文基于蒙特卡洛和粒子群优化算法，利用Matlab对算法进行实证分析，将环保-经济的多目标转化为单目标问题，对将电动汽车这一具有剩余电量的随机性的移动式储能接入到微电网规划之中，构建仿真模型进行系统成本最低寻优，并与不计入电动汽车的微网系统进行数据比较．在验证模型有效性的同时，也得出电动汽车的储能特性在满足系统负荷需求的要求基础上能够有效降低环境及系统总成本．不足之处在于没能够将各个地方政府的宏观调控与相关促进电动汽车推行等难以量化的指标考虑到算法中去，这个问题将在后续研究中继续展开．