基于PSO-BP神经网络的砂岩三轴抗压强度预测
2019-05-15郭永成朱千凡
晏 斌 郭永成,2,3 朱千凡 胡 鹏
(1.三峡大学 土木与建筑学院,湖北 宜昌 443002; 2.三峡大学 防灾减灾湖北省重点实验室,湖北 宜昌 443002; 3.三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002)
在工程实际的建设及使用过程中,岩体工程的工程特性会随着其赋存的地质环境变化而改变.闻磊等[1]冻融循环试验研究不同温度区间冻融循环下饱水花岗岩力学性质的变化;戎虎仁等[2]研究发现温度在300℃红砂岩的单轴抗压强度为常温下的1.4倍;彭守建等[3]进行了不同孔隙水压下的砂岩剪切破坏试验.以上学者系统地研究了单一温度、孔隙水压对岩体力学性质的影响,或者运用数值模拟的方法研究了二者共同作用下的岩体力学性质的变化,但对三场耦合作用下岩体力学特性变化的试验研究相对较少.
刘立峰等[4]将量子粒子群与神经网络相结合,建立了研究区的流体识别模型;邓传军等[5]建立了粒子群优化神经网络模型预测建筑物的沉降;胡军等[6]利用协调粒子群算法和BP网络建立了边坡稳定性CPSO-BP预测模型来分析边坡的稳定性;E.Avunduk等[7]以岩石抗压强度等因子为输入层建立人工神经网络模型来预测掘进机的瞬时切削速率.以上学者的研究,将各种算法模型运用到岩石力学的研究之中,从而规避了实际工程中部分参数无法直接获取的技术难点.故本文拟将粒子群算法、BP神经网络、岩石力学数值模拟3者结合起来,预测岩体力学中的相关指标.
1 岩石强度试验
在TOP INDUSTRIE岩石三轴试验仪上,对饱和标准砂岩(50 mm×50 mm×100 mm)进行温度场、渗流场、应力场耦合试验,分4个阶段进行:①利用温度控制系统加热至设定目标值(5℃、20℃、40℃、60℃),恒温6 h使试样均匀受热;②以12 bar/min(1.2 MPa/min)的速度,将围压加载至预设围压值5 MPa;③以0.1 bar/min(0.01 MPa/min)的速度加载孔隙水压至目标值(0 MPa、0.3 MPa、0.6 MPa、0.9 MPa),并维持恒定30 min;④以12 bar/min(1.2 MPa/min)的速度加载轴压,直至试样破坏.将试验过程中所测得的参数以及试验最终的结果作为后文所建立模型的数据样本,从而完成后续的研究工作.
2 BP神经网络算法
2.1 BP神经网络模型
图1为神经网络结构示意图,输入层提供输入数据之后,进行学习与迭代,神经网络的权阀值进行更新,同时根据误差反馈原理,将误差反馈到输入层,不断更新权阀值.

图1 BPNN结构图
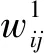
(1)
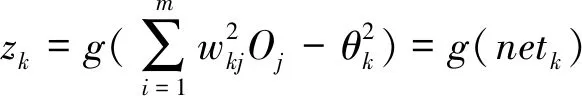
(2)
其中,f为隐含层传递函数;g为输出层的传递函数.则训练误差为:
(3)
误差E对输入层与隐含层神经元间的权值求偏导得到:
(4)
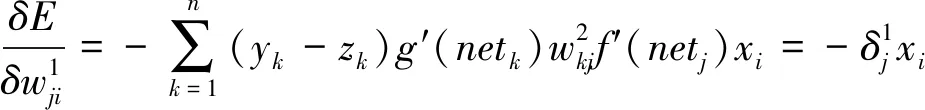
(5)
通过权值调整公式得到调整后的权值为:
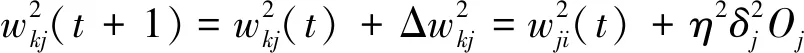
(6)
其中,η1,η2分别为隐含层和输出层的学习步长.
2.2 参数设置
如图2所示,在BP神经网络中将前文试验数据(见表1)中编号为4、7、10、16的数据作为预测样本,其余为训练样本,并预测目标即峰值强度.故确定神经网络的输入包括p1:岩样重量;p2:岩样直径;p3:岩样高度;p4:测试声波传播时间;p5:试验温度;p6:孔隙水压强度;p7:粘聚力;p8:内摩擦角;p9:主破裂角;p10:峰值应变.最大迭代次数设置为1 000,学习率设置为0.1,动量因子设置为0.9.
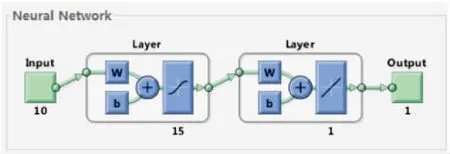
图2 BP神经网络结构设置
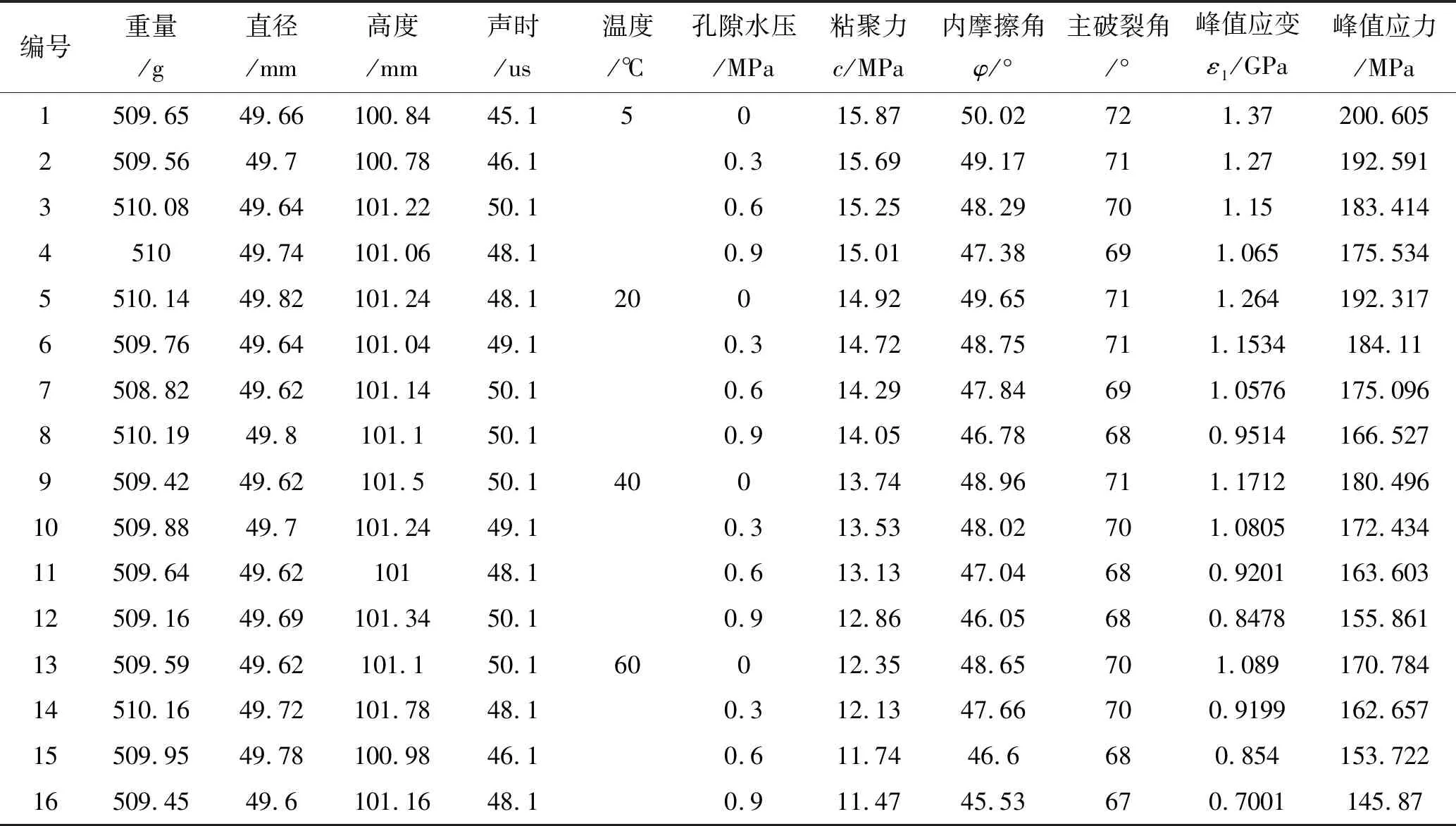
表1 试验结果统计表
2.3 结果分析
通过Matlab编程,计算预测出的砂岩三轴抗压强度值如图3所示,可以看出BP神经网络模型预测的误差最大可达10.1%,平均误差为6.105%.运用SPASS软件分析得到预测值与实验值之间的相关性系数为0.556.由此可见,利用BP神经网络模型可以预测多因素影响条件下的砂岩三轴抗压强度值,但其相关性还有待提高.
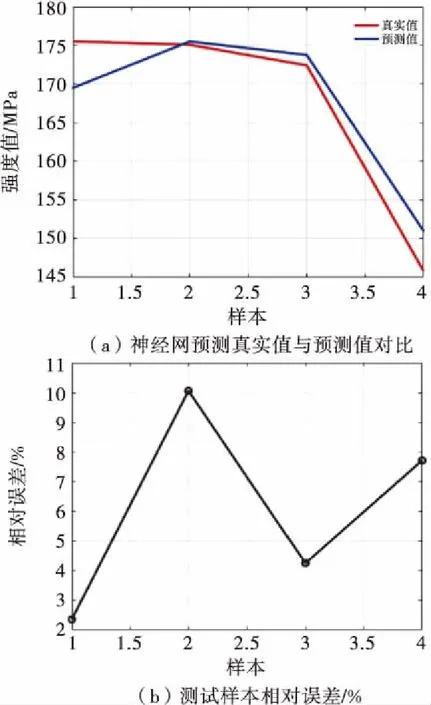
图3 预测结果图
3 粒子群算法优化的BP神经网络模型
3.1 粒子群算法
粒子群算法是一种模拟鸟类在飞行空间(即求解问题的搜索空间)里搜寻食物(即最优解)的过程.假定在D维空间中,粒子坐标Xi=(xi1,xi2,…,xiD),速度Vi=(vi1,vi2,…,viD),粒子目前最优位置(即个体极值)为Pbest=(pi1,pi2,…,piD),整个粒子群目前最佳位置(即全局极值)gbest=(g1,g2,…,gD).粒子根据如下式(7)和式(8)来更新自己的速度和位置:
vij(t+1)=wvij(t)+c1r1(t)[pij(t)-xij(t)]+
c2r2(t)[pgj(t)-xij(t)]
(7)
xij(t+1)=xij(t)+xij(t+1)
(8)
其中,c1、c2表示学习因子,r1、r2表示[0,1]范围内的均匀随机数.w较大,则式(7)全局收敛性较强,局部收敛性较弱;w较小,则式(7)局部收敛性较强,全局收敛性较弱.运用公式(9)的调整方式,给予w从大到小的赋值,则可权衡算法的搜索能力.
(9)
其中,Tmax表示最大进化代数;wmin表示最小惯性权重;wmax表示最大惯性权重;t表示当前迭代次数.
3.2 PSO-BP神经网络预测模型的构建
同前文所建BP神经网络模型一样,以相同的10个因子作为输入样本,以抗压强度为输出层,设置15个隐含层.粒子群算法的参数设置为:学习因子c1=c2=1.49,进化次数为Tmax=50次,种群规模为N=10个,惯性权重最大wmax=0.9,wmin=0.4,粒子的初始化速度在[-1,1] .建立粒子群优化的神经网络模型的技术路线图如图4所示.
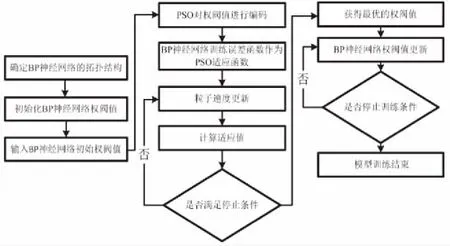
图4 SPO-BP神经网络技术路线图
3.3 预测结果
利用Matlab编程计算出岩石在温度场作用下砂岩三轴抗压强度试验值与预测值见表2.利用粒子群算法优化的BP神经网络模型预测温度场作用下砂岩偏应力-渗透水压耦合试验中的峰值强度的最小误差为0.72%,最大误差为4.37%,误差平均值为2.16%.

表2 试验结果及预测值
由图5可看出,PSO-BPNN模型相较于BPNN的预测精度有了一定的提高,平均误差较BP神经网络模型的则有了很大的提高.其原因在于粒子群算法对BP神经网络的权阀值调整进行优化,使预测值能够达到全局最优,避免BP神经网络模型陷入局部最优解的缺陷,使模型精度得以提升.
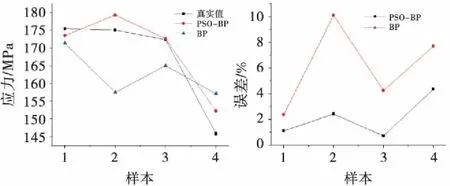
图5 PSO-BP和BP神经网络模型结果对比图
虽然建立的粒子群优化BP神经网络模型对于预测砂岩温度场作用下应力-渗透水压作用下的峰值强度具有精确、快速的特点,但模型的精确度由输入样本的精确度和数量来决定.由此,通过试验获得大量、精准的试验数据,是提高预测模型精度的有效之法.
4 结 语
本文基于三场耦合试验所测得的试验数据及结果,建立粒子群算法优化的BP神经网络预测模型,并将预测值与试验结果进行对比,计算预测的误差值.由此得到以下结论:
1)建立了BP神经网络模型和PSO-BP神经网络模型,对温度场、渗流场、应力场耦合作用下砂岩峰值抗压强度进行了预测,对比发现预测值与试验真实值之间的误差较小,从而证明模型的可行性,可快速、精准地计算出砂岩的三轴抗压强度.
2)粒子群优化的BP神经网络预测模型相较于传统的BP神经网络模型,预测精度有了一定的提升,误差较小,预测值与实验值之间的相关性有了较大提升,对于解决实际工程中部分参数无法获取的难点有一定的应用价值.
