基于三维加速度椭球法的液货舱内部压力解析算法
2019-05-15付喜华
付喜华
(中国船级社 规范与技术中心, 上海200135)
0 引 言
2016年生效的《国际散装运输液化气体船舶构造与设备规则》(InternationalCodefortheConstructionandEquipmentofShipsCarryingLiquefiedGasesinBulk,下文简称IGC 规则)[1]在围护系统载荷计算方法上作了重要修改,即考虑船舶纵向运动产生的纵向载荷的影响,用三维加速度椭球法替代了上一版IGC 规则中的二维加速度椭圆法。各船级社液化气体船规范指南也根据新IGC 规则进行了更新[2-4]。使用三维加速度椭球法计算液货舱内部压力,增大了计算难度,但得到的载荷结果更加接近船舶实际情况,更趋于合理。
现行的迭代法计算液货舱内部压力基于对椭球法定义的任意空间角度(两个维度)的迭代数值计算法开展[5-6],需要完成两个空间维度的反复迭代。运算次数与迭代步数的平方成正比,计算效率较低,且计算结果的精确度受设置两个角度的迭代步长影响。
为了改善上述迭代法的不足,提升计算效率和精度,基于新IGC 规则中的加速度椭球分析法,通过构造三维坐标系,依据立体几何和三维向量理论,推导任一计算点基于液货舱边界某一特定点的内部压力的解析解表达式,并编制迭代法数值计算程序。通过实例计算比较上述两种方法的计算结果。
1 新IGC 规则内部压力计算规则
根据新IGC 规则[1]的描述,液货舱内部压力由设计蒸气压力P0和舱内液体货物运动产生的压力Pgd两部分组成。Pgd的计算尤为关键,可由下式计算得到
(1)
式中:ρ为液货的密度;aβ为在任意的β方向上,由重力和动载荷引起的无因次加速度;zβ为从计算点到液货舱边界上高于计算点的各点在方向β上的液货高度,m。其中,β为加速度椭球内任意无因次加速度与重力加速度的合成加速度方向,动载荷引起的加速度由加速度椭圆或椭球决定。
aβ纵向、横向和垂向的最大加速度分量axx、ayy和azz在IGC 规则中有明确的简易计算方法。新IGC 规则给出了显示最大加速度分量的三维加速度椭球示例[1],如图1所示。zβ计算示例如图2所示。
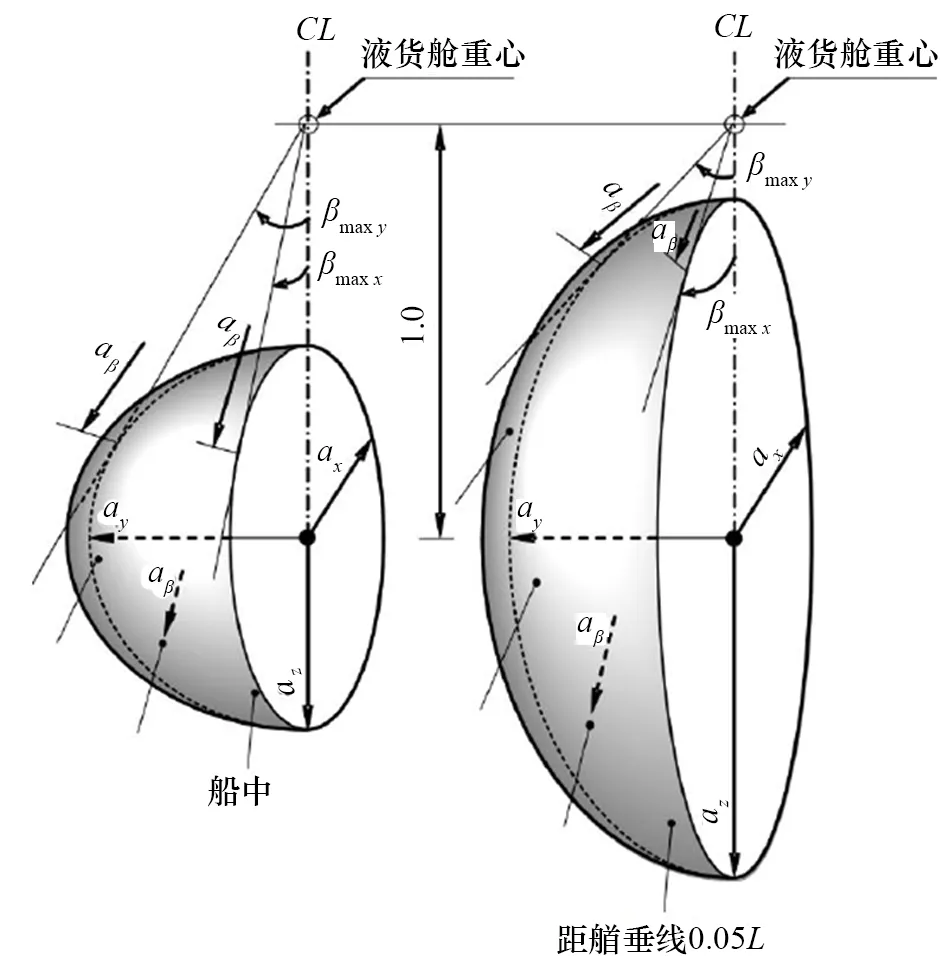
图1 加速度椭球

图2 zβ计算示例
2 加速度椭球迭代计算法
采用基于新IGC 规则的加速度椭球迭代法计算的原理是:通过设定纵向和横向两个方向的迭代角度α(i)和γ(j),在任意加速度方向上开展内部压力的迭代计算,完成整个加速度椭球的搜索后确定内部压力的极大值[5]。加速度椭球迭代法如图3所示。
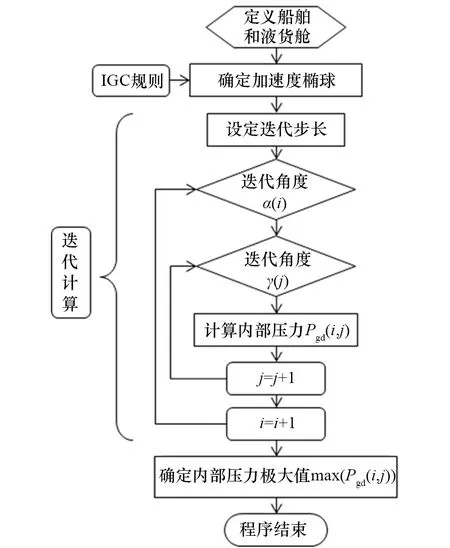
图3 迭代计算法流程
迭代法需通过反复迭代完成基于任意加速度方向的内部压力数值计算,过程繁冗,运算次数是解析解法的千倍,计算时间较长;不同的程序设计开发人员对迭代步长α(i)和γ(j)的设定不同,没有统一的标准;设定较大迭代步长影响计算结果的精确度,而较小的步长将大幅增加计算时间,影响计算效率。
3 加速度椭球解析计算法
建立如图4所示的坐标系:以液货舱加速度椭球的中心为原点建立空间坐标系,船长方向为x坐标轴(船首方向为“+”),船宽方向为y坐标轴(左舷为“+”),型深方向为z坐标轴(向上为“+”)。
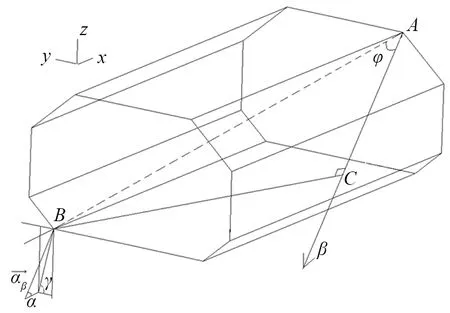
图4 参考液货舱边界及坐标系
液货舱边界特定点A的坐标为(x0、y0、z0),计算点B的坐标为(x1、y1、z1),得到
AB=(x1-x0,y1-y0,z1-z0)
(2)
通过A点沿加速度β方向做1条直线,B点在该直线上的投影为C点,φ为AB与AC的夹角,可得|AC|即为A点到计算点C点在方向β上的液货高度zβ:
zβ=|AC|=|AB|×cosφ
(3)
加速度椭圆参数方程可表示为
(4)
式中:α为加速度与x轴的夹角;γ为加速度在yOz面上的投影与y轴的夹角,如图4所示。
上述加速度与重力加速度合成,即可得
aβ=(axxcosα,ayysinαcosγ,
-1+azzsinαsinγ)
(5)
加速度αβ与在方向β上液货高度zβ的乘积可表示为
αβzβ=|aβ|×|AC|=|aβ|×|AB|×cosφ
(6)
根据向量的数量积理论可知
aβ·AB=|aβ|×|AB|×cosφ
(7)
由式(6)、式(7)可以得出:
αβzβ=aβ·AB
(8)
将式(2)、式(4)代入式(8),依据向量数量积算法可得
αβzβ=ax×(x1-x0)+ay×(y1-y0)+
(-1+az)×(z1-z0)
(9)
将式(4)、式(5)代入上式(9),得到
αβzβ=axx(x1-x0)cosα+ayy(y1-y0)·
sinαcosγ+azz(z1-z0)sinαsinγ-(z1-z0)
(10)
式(10)可以表达为
αβzβ+(z1-z0)=acosα+bsinαcosγ+csinαsinγ
(11)
式中:
(12)
将式(11)、式(12)定义的椭球参数方程转换成标准方程,可以得到
αβzβ+(z1-z0)=x+y+z
(13)

(14)
显然,αβzβ+(z1-z0)的极大值可以理解为式(14)表示的椭球与式(13)表示的空间平面相交或相切情况下形成的平面与原点之间距离的极大值。
通过三维立体几何知识及运算可得到
(αβzβ)max=-(z1-z0)+
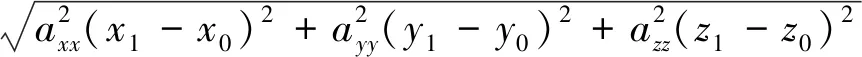
(15)
根据三角函数算法,式(15)达到极大值时,α、γ满足以下条件
(16)
(17)
将式(15)代入式(1)中,即可得到基于某一特定点的内部压力的解析计算公式为

(18)
加速度椭球形解析法流程如图5所示。
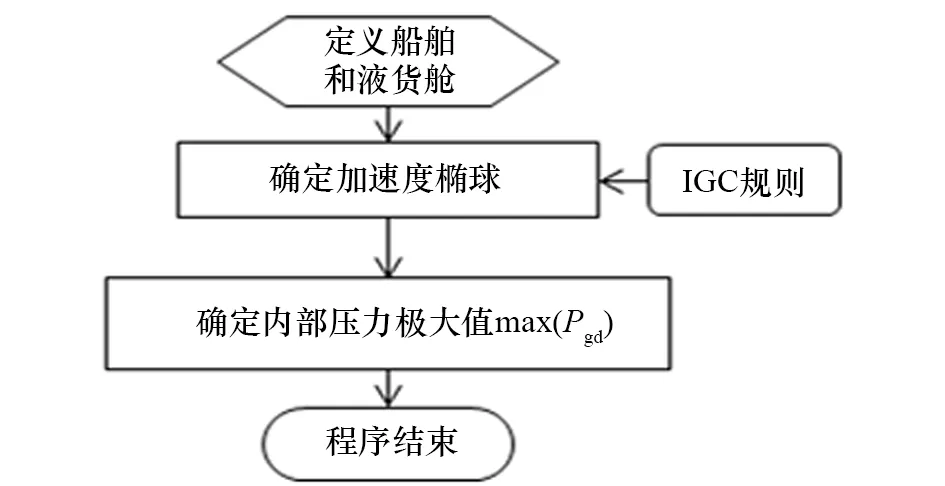
图5 加速度椭球形解析法流程
4 算 例
为了验证上述推导的准确性以及比较解析解法与迭代法的差异,编制迭代算法计算程序,对某薄膜型LNG运输船某液货舱进行Pgd的迭代计算,并将计算结果与基于加速度椭球解析法的计算结果进行比较。为了保证计算精度,加速度椭球角度迭代步数分别设定为40(纵向)和100(横向)。图6所示为薄膜型LNG船的液货舱边界及边界上的10个计算点。
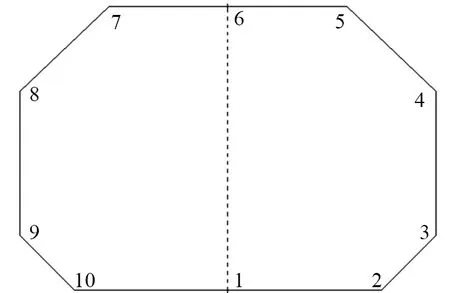
图6 液货舱边界计算点
对图6所示液货舱分别采用解析法和迭代法得到图示10个计算点的Pgd计算结果,如表1所示。
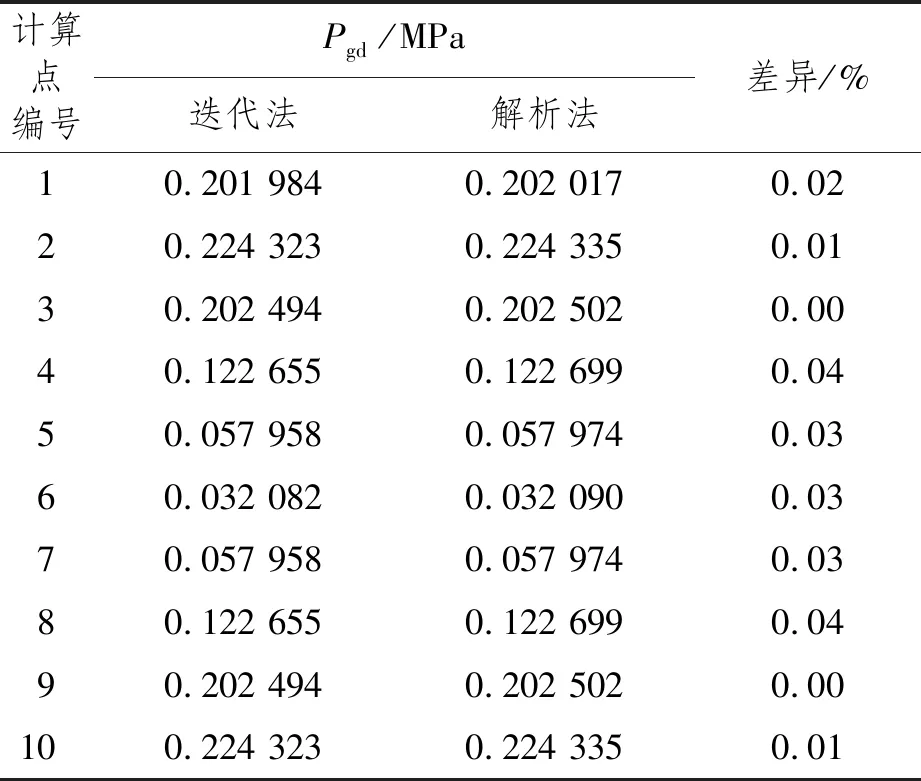
表1 解析法与迭代法(加速度椭球法)计算结果比较
从表1可以看出,解析法和迭代法的计算结果呈现以下特征:
(1) 解析计算的结果微大于迭代计算的结果,符合解析解为极大值的客观实际;
(2) 由于选取的角度迭代步长较小,纵向和横向迭代次数分别为40次和100次,迭代步长小于1°,精度得到了很好的控制,迭代计算结果与解析算法结果非常接近。
分别采用加速度椭球法和加速度椭圆法对图5所示计算点进行Pgd计算。表2比较了计算结果差异,可以看出:
(1) 由于椭球法考虑了船舶纵向运动产生的载荷影响,计算结果略大于椭圆法的结果,除了内甲板外,相差最大处不大于4%;
(2) 由于内甲板位置处纵向运动产生的载荷在内部压力中占比较其他位置大,所以在点6处两种方法的计算结果差异较大。
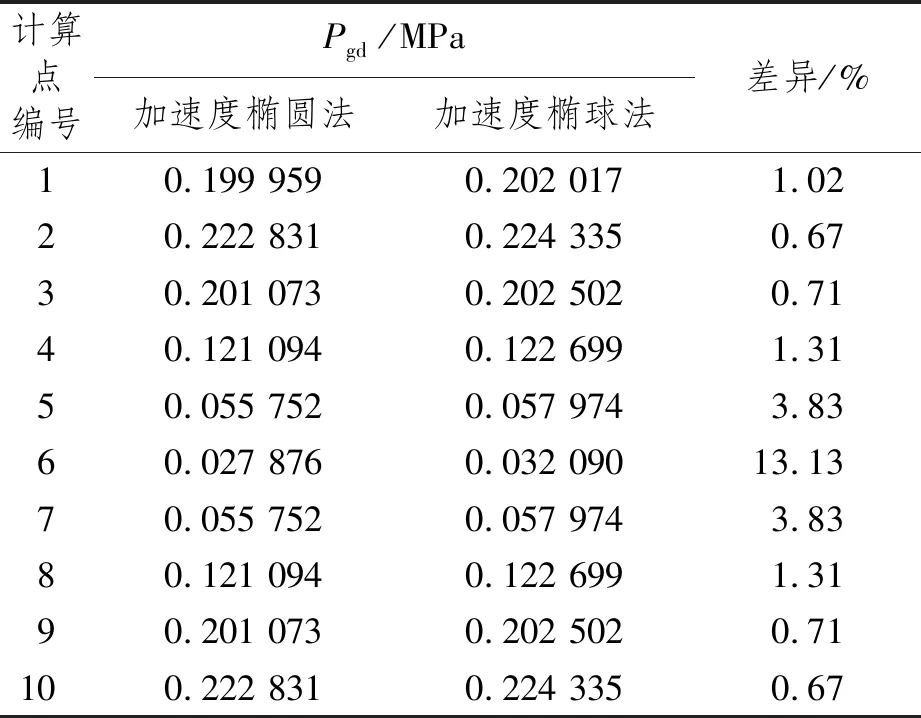
表2 加速度椭圆法与加速度椭球法(解析法)计算结果比较
最后,对基于上述3种方法完成的液货舱10个计算点的Pgd计算所花费时间分别进行了统计,如表3所示。

表3 3种计算方法的计算时间 s
由表3可以看出:
(1) 解析法的计算效率远远高于迭代法,计算时间仅为迭代法计算时间的1/1 063;
(2) 三维加速度椭球法与二维加速度椭圆法计算效率相近,计算时间相近。
5 结 论
通过基于椭球法的内部压力解析解的理论推导,
以及实例计算验证,得出加速度椭球解析算法具有计算结果准确、运算效率高、简单易用的优点,为设计人员开展内部压力计算及其液货舱结构尺寸设计提供重要帮助和依据。
