空船重量重心估算方法的分析

晋文菊, 樊红元,顾剑刚

(上海船舶研究设计院，上海 201203)

0 引言

船舶初步设计阶段的空船重量和重心位置的估算是一项具有挑战性的工作，尤其是如果新船参数与型船的只有部分或完全不同时,缺少系统的经验数据使得估算工作很困难或造成结果很多的不确定性因素。由于缺少空船重量估算系统性的研究，因而设计者的经验和理解对最终结果的精度起着关键作用。

历年来有大量船舶设计人员致力于空船重量的估算工作[1-4](下文中提到“空船重量的估算”同时也包括“重心位置的估算”)，同时在施工阶段着力研究对空船重量的控制及优化[5-6]。本文将近年来的主要估算方法进行汇总并分析比较，供船舶设计人员在估算空船重量时作参考。

1 从两个吃水的载重量估算空船重量

1.1 研究过程

该方法[1]为在已知某船的主要尺度参数船长L、型宽B、设计吃水Td和结构吃水TS以及相应吃水下的载重量dwS的基础上估算空船重量。其主要步骤如下：

(1)假设两个方形系数Cb(Cb1、Cb2)及其相应的水线面系数CW(CW1、CW2)。

(2)计算假定的Cb设计吃水时的排水量。

Δ1=γkLBTdCb1

Δ2=γkLBTdCb2

式中：Δ1为假设的方形系数1的排水量，t；Δ2为假设的方形系数2的排水量，t；γ为水的密度，t/m3；k为船壳板系数；Cb1为假设的方形系数1；Cb2为假设的方形系数2。

(3)按步骤(2)中的及已知设计吃水时的载重量，计算相应的空船重量LS(LS1、LS2)。

LS1=Δ1-dw

LS2=Δ2-dw

式中：LS1为假设方形系数1对应的空船重量，t；LS2为假设方形系数2对应的空船重量，t；dw为船舶已知设计吃水下的载重量，t。

(4)估算结构吃水时的排水量。

式中：ΔS1为假设方形系数1时船舶结构吃水时对应的排水量，t；ΔS2为假设方形系数2时船舶结构吃水时对应的排水量,t；CW1为假设的方形系数1对应的水线面系数1；CW2为假设的方形系数2对应的水线面系数2。

(5)按步骤(3)计算得到的空船重量LS值与已知结构吃水时的载重量dwS计算结构吃水时的排水量ΔS′。

ΔS1′=LS1+dwS

ΔS2′=LS2+dwS

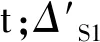
(6)计算结构吃水时两排水量的差值δΔS。

δΔS1=ΔS1′-ΔS

δΔS2=ΔS2′-ΔS

式中：δΔS1为假设方形系数1时对应的计算结构吃水与母型船结构吃水相应的排水量之差，t；δΔS2为假设方形系数2时对应的计算结构吃水与母型船结构吃水相应的排水量之差，t。

(7)将δΔS1与δΔS2分别代入线性方程y=ax+b求解。具体方法如下：

解出a和b，然后求出y=0时对应的x值，即求出δΔS=0时相应的方形系数Cb0。

(8)最后按Cb0计算出Δ0及LS0。

举例说明，某36 000 t散货船L=179.9 m，B=30.0 m，Td=9.5 m，dw=33 417 t，TS=10.0 m，dwS=35 954 t。估算结果见表1。

表1 36 000 t散货船空船重量一次估算

调整水线面系数，进行第二次估算，见表2。

实船的空船重量LS=9 398 t。

从以上两个算例中不难看出，本方法的估算精度取决于CW/Cb的取值。

1.2 方法分析

公开资料发表的型船资料，基本上没有明确给出空船重量，使得设计者在应用时感到欠缺。本方法的优点是便于利用型船资料。但是从上述算例不难看出，CW/Cb的取值至关重要，不然会影响本方法的精度，因此设计者应该注意收集完工船舶的Cb值及对应的CW值。

表2 36 000 t散货船空船重量二次估算

2 BP神经网络应用于散货船空船重量估算

2.1 研究过程

BP神经网络是具有三层或三层结构以上的神经网络，包括输入层、中间层(隐藏层)和输出层。文献[2]利用BP神经网络建立三个模型与统计回归模型的估算结果进行比较。

此方法中空船重量神经网络各层之间实现全连接，而每层神经元之间无连接。每一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播，在输出层的各神经元获得网络的输入响应。为了减少目标输出与实际情况之间的误差，从输入层经过各中间层逐层修正各连接权值，最后回到输入层。随着误差逆向传播修正的继续进行，网络对输入模式响应的正确率不断上升[3]。

2.2 方法分析

文献[2]以10艘散货船作为测试样本，建立3种神经网络模型。模型1以船长L为输入变量，空船重量LW作为输出变量；模型2以装载重量DW为输入变量，空船重量LW作为输出变量；模型3以船长L、型宽B、型深D作为输入变量，空船重量LW作为输出变量。将3种模型的测试结果与传统统计回归模型的测试结果进行比较，结果证明3种神经网络模型的结果精度均比统计回归模型的结果更接近实际值，相对误差较小，均控制在10%以内。同时3种神经网络模型中的模型3因考虑了船舶的船长L、型宽B和型深D为影响空船重量的主要因素，比其余2种模型考虑更为全面，测试的结果也最为精确，测试结果与实际值的偏差在0.02%～1.9%。但是，该方法对设计人员神经网络知识的要求较高，不便于普及。

3 统计回归方法

3.1 研究过程

所有统计回归方法包括BP神经网络模型估算都是基于事先建立的详细的数据库，即搜集的母型船数据。母型船数据的收集是一个长期细致的工作，设计人员在收集数据时应在交船完工测得实际空船重量后及时更新数据库。

在数据库中如何分解船舶结构是影响估算精度的关键因素，分解结构越详细，估算的偏差就越小。通常，随着船舶建造阶段分解结构重量和重心估算的详细程度的增加，估算的不确定性因素会逐渐减少。船体结构分组示意图见图1。通常来讲结构划分越详细，骨材重量和重心的估算越灵活和匹配。鉴于最详细的等级划分一般都是固定的，因此划分过程中尽可能多的级别子群组对估算工作是有益的。其余专业可在结构分段的基础上，在每个区域内依据设备分类进行划分。数据库中每艘船舶的每一分组根据影响单项重量的因素进行统计回归分析。船舶重量结构划分示意见图2。

图1 船体结构分组示意图

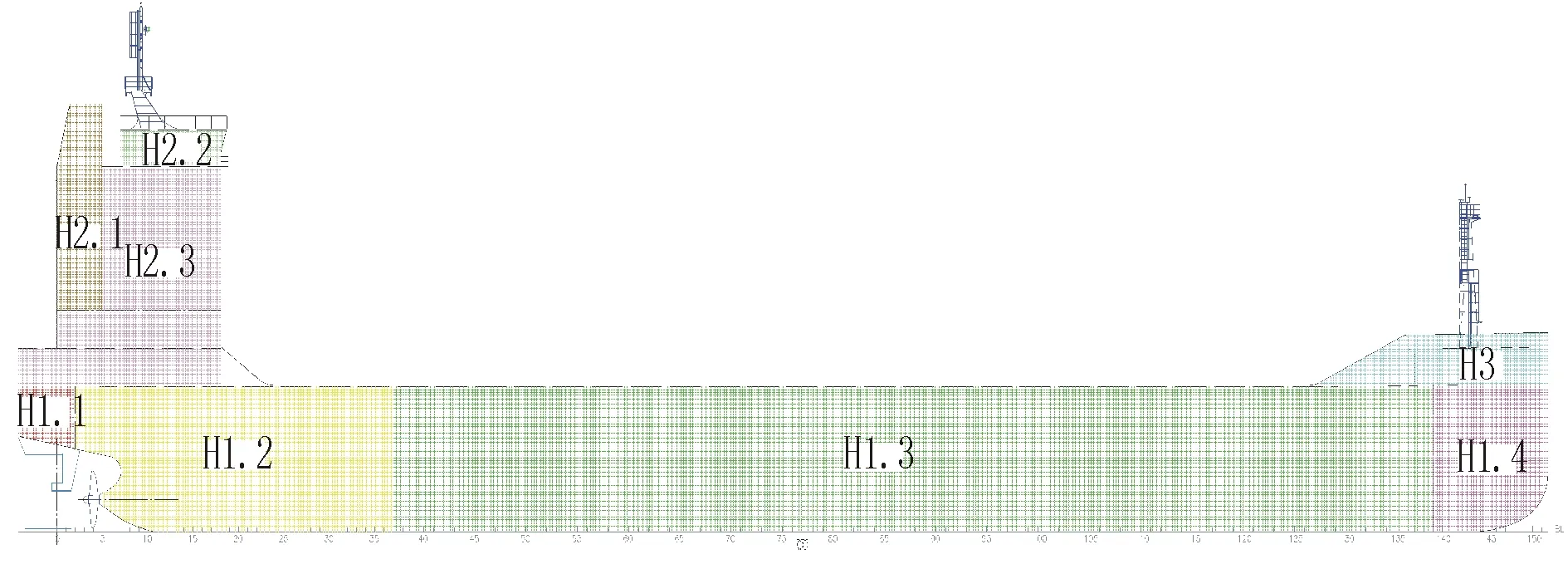
图2 船舶重量结构划分示意图

新估算船舶若有姐妹船的情况下，统计回归分析的结果比较精确，划分等级也可略微简单一些；若无姐妹船的参考，划分群组应尽量详细。

同时，估算空船重量时所参考的母型船的特点也是设计师应该注意的。在数据库中已有船舶模型参数基础上进行回归时，船舶特点的差异性也可能造成回归系数的变化较大。例如：在估算无冰区要求的船舶时，如果数据库中模型数量足够的话，在统计回归时，应将无冰区要求的船舶模型排除在外，以提高空船重量系数的精确度从而提高估算准确度。

3.2 方法分析

统计回归方法是目前应用最普遍且实用性最高的方法。设计人员在从事空船重量的估算工作时，重量偏差的计算也是非常有必要的。重量估算的偏差可以通过各分组回归曲线的离散情况计算而得，即计算各分组的标准偏差[4]。对于大的偏差应分析具体原因，譬如是否同样的参考船有冰区要求，是否主机功率略大一些等原因，以利于后面其他新船估算工作更精确的开展。在重量估算方法中，认为子群组之间统计上相互独立，尽管实际上这不是完全正确的，但是与假定总体相关性更接近设计情况。该方法随着设计人员数据库与经验的积累，估算精度会越来越高。

4 结语

空船重量的重要性贯穿于船舶的整个寿命周期中，空船重量估算结果可能是赢得船舶建造合同的关键因素。文中三种估算方法各有优缺点，“从两个吃水的载重量估算空船重量”的方法适用于设计初期阶段并缺少更为详细的参考船型的情况下；而“BP神经网络估算空船重量”的方法只适用于个别掌握此项技术的设计人员，不具有推广性；“统计回归方法”则是更为普通的估算方法，但是统计回归则是一项长期的任务，只有具有更为详尽的数据库才可以将船型归类分组得出精确的空船重量系数。实际设计工作中，设计人员应结合搜集资料的实际情况来确定选用的估算方法，使得估算工作可以精确而又有效的进行。