履带车辆履带预张紧力对平顺性的影响与仿真
2019-05-14卞美卉杜志岐
卞美卉, 张 洋, 杜志岐
(中国北方车辆研究所,北京 100072)
履带车辆的平顺性直接取决于悬挂装置的性能,然而履带作为行动系统的重要组成部分,它的受力情况必然对平顺性有一定的影响.张紧力过大,履带刚度太大,起不到缓冲作用,会增加履带和底盘部件摩擦,能耗严重,并有断带危险;张紧力过小,使得履带松弛,容易脱带、爬齿,造成履带失效,车辆瘫痪[1].履带预张紧力是影响履带张紧力的主要因素之一.当前在履带车辆行动系统设计时,履带预张紧力的计算一般采用经验公式,以车重乘以一个经验系数作为履带的预张紧力.为了分析履带预张紧力对车辆平顺性的影响,以某型高速履带车辆为例,在多体动力学仿真软件RecurDyn中建立了整车动力学模型,在不同车速下分别取车重的6%、8%、10%、12%为履带预张紧力对车辆平顺性进行了仿真.
1 履带预张紧力的理论分析
履带车辆行驶时作用于履带上的力分为恒定力(预张紧力、牵引力和由于离心力产生的张力)和交变力(由于履带、负重轮和车体的纵向和横向振动,啮合不均匀和履带的板块结构等产生的动载荷)[2].车辆在静态状况下,履带环被预张紧力Fyz拉紧.当车辆行驶时,由于履带板位移方向变化产生的离心力Fl为:
Fl=mdv2.
(1)
式中:md为履带的单位长度质量;v为车辆行驶速度.
一般情况下,离心力产生的张力与履带环全长上的预张紧力方向相同.当采用弹性履带时,离心力的作用使履带变长,在诱导轮位置固定的情况下,会使预张紧力变小,弹性履带的预张紧力F′yz按式(2)计算.
(2)
式中:K为说明履带挠度和行驶部分结构的系数.对于装用弹性履带的履带行驶装置来说,K=0.2~0.5.
履带环非工作段的张力的恒定分量由式(3)表示.
(3)
式中:Fq为牵引力;Ls为履带松边长度;Lj为履带紧边长度.
将前述弹性履带的预张紧力F′yz表达式代入式(3)后,Ffz变为式(4)形式.
(4)
履带环工作段的张力由非工作段的张力恒定分量和牵引力组成,如式(5)所示.
Fgz=Ffz+Fq.
(5)
本研究的某型高速履带车辆采用主动轮前置的形式,其非工作段的张紧力和工作段的张紧力的分布如图1所示,图示力的大小和张紧力的方向是互相垂直的.

图1 作用于履带环上的张紧恒定力
由图1可知,主动轮前置的车辆履带最小张紧力出现在履带的前斜支段.当Ffz≈0时,最可能出现履带脱落或履带啮合不良的现象.首先是在最大的牵引力(Fqmax)作用时,可能出现这种履带松弛的现象.假定此时的行驶速度不高Fl≈0,由式(4)可得到求预张紧力的条件方程式为:
(6)
在主动轮前置的条件下,比值Ls∶Lj=0.08~0.14,相应地要求较大的预张紧力Fyz≈0.9Fqmax.
2 履带车辆的平顺性仿真
为了分析履带预张紧力对平顺性的影响,在多体动力学仿真软件RecurDyn中建立整车动力学模型并进行平顺性仿真.
2.1 构造整车动力学模型
车辆的计算参数如表1所示.在Creo软件中按照实际尺寸和结构建立车体模型,将车体简化为集中质量的刚体,然后导入到RecurDyn中.

表1 某型履带车辆计算参数
利用RecurDyn的高速履带模块Track-HM对主动轮、负重轮、诱导轮、托带轮及履带板按实际尺寸建模[3],用Assembly功能组装履带(图2).构建的整车模型如图3所示.

图2 Track-HM模块

图3 RecurDyn整车动力学模型
添加车体和行动系统各部件模型之间的约束关系:主动轮、诱导轮、托带轮和车体之间为旋转副;负重轮通过旋转副和平衡肘相连;平衡肘的另一端通过旋转副和固定在车体的扭杆相连.在平衡肘和扭杆相连的旋转副处创建扭转弹簧阻尼器RSDA(RotationalSpring),将悬挂装置的刚度和阻尼特性换算为扭转弹簧的刚度(Spring Coefficient)和阻尼(Damping Coefficient),负重轮载荷换算为预扭矩(Pre Torque),在此建立刚度和阻尼的等效特性约束.将动力推进装置简化为驱动左、右主动轮的旋转速度,通过定义RecurDyn自带的一般阶跃函数STEP(TIME,0,0,t,ω)来实现车辆的运动.其中,t为加速时间,ω为目标车速换算的最终旋转角速度.
分别取车重的6%、8%、10%、12%为履带预张紧力Ffz,在履带环(Pin Bushing)的属性里定义预张紧力(Pre Load)的值.
2.2 构造路面模型
利用路面不平度对仿真路面进行建模.大量的试验表明,路面不平度是零均值的Gauss随机过程,国际标准ISO/TC108/SC2N67和国家标准GB7031-2005建议采用式(7)的路面功率谱密度表达:
(7)
式中:n为空间频率,是路面波长的倒数;n0为参考空间频率,n0=0.1m-1;W=2为频率指数;Gq(n0)为参考空间频率下的路面功率谱密度值,称为路面不平度系数.
该标准中路面不平度按路面功率谱密度的几何平均值分为8级,其中D级、E级、F级的路面不平度系数和路面高度均方根值如表2所示.
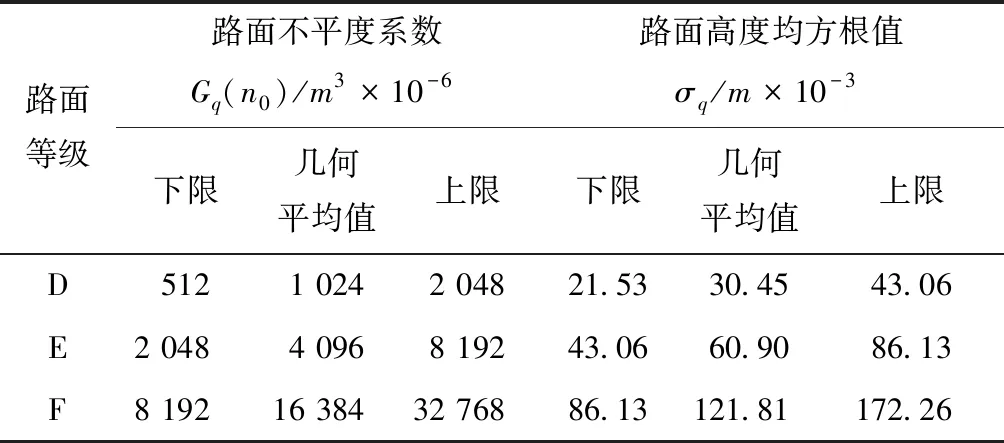
表2 路面不平度的分级标准
对照上述国际标准和国家标准,用于履带车辆经常试验的野外路面相当于该标准中的E级路面.用Matlab软件按标准路面不平度系数的值仿真出E级路面,其路面不平度曲线如图4所示,自功率谱密度在双对数坐标下的曲线如图5所示.

图4 E级路面不平度曲线
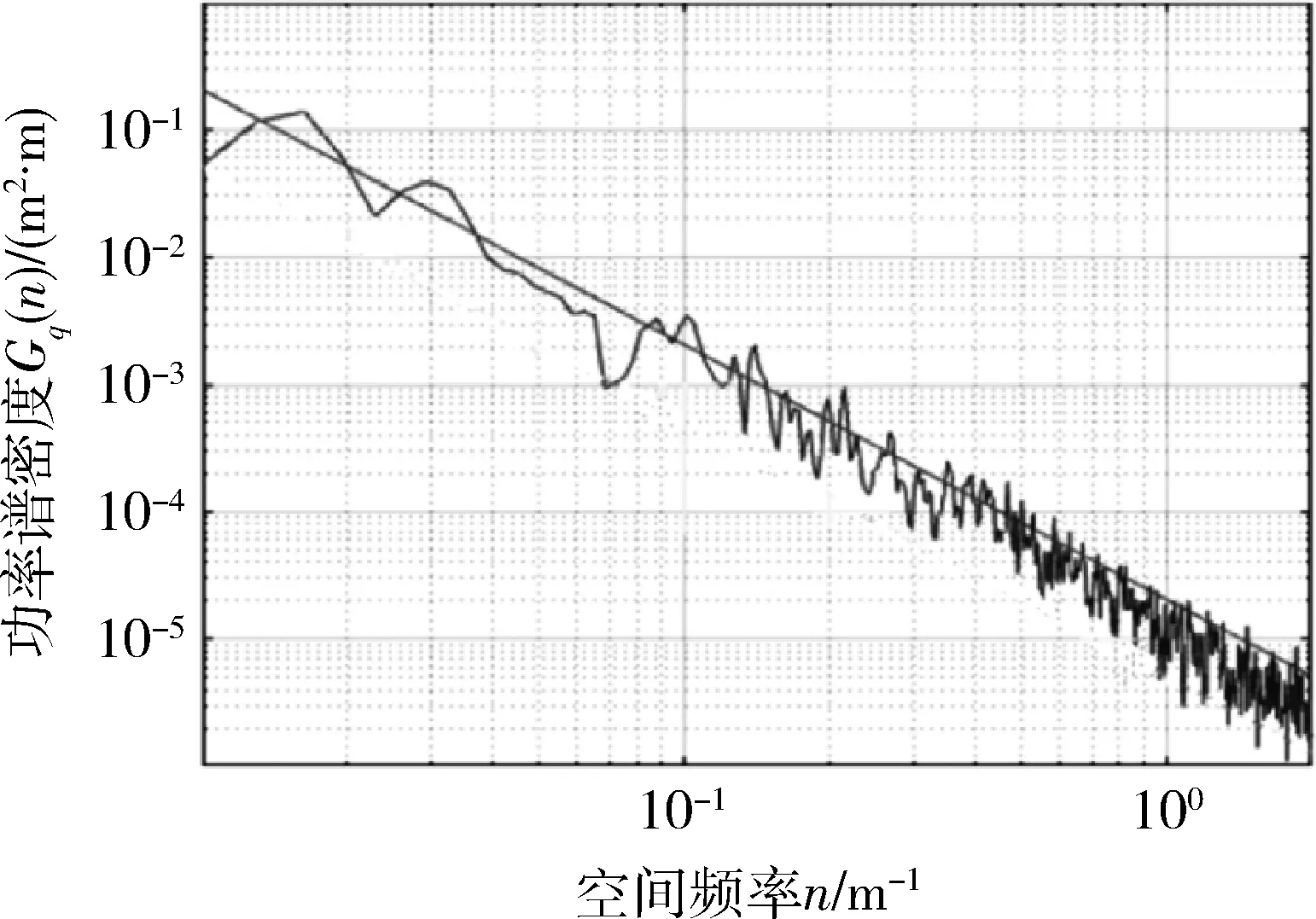
图5 功率谱密度在双对数坐标下的曲线
3 仿真结果分析
令车辆模型分别以20 km/h,30 km/h,40 km/h,45 km/h的车速进行平顺性仿真,设置加速时间为5 s,仿真总时长15 s,得到车辆驾驶员座椅处垂直振动加速度信号.图6为车辆模型以20 km/h行驶的加速度时间历程a(t)的曲线.
根据ISO2631-1997,在进行平顺性评价时,人体对不同频率振动的敏感程度不同,用加权加速度均方根值aw来评价振动对人体的影响.对仿真得到的加速度时间历程a(t)进行频谱分析得到功率谱密度函数Ga(f),如图7所示.
再按式(8)计算加权加速度均方根值aw.
(8)
式中:W(f)为不同频率的加权系数.ISO2631-1997给出W(f)的值见表3.
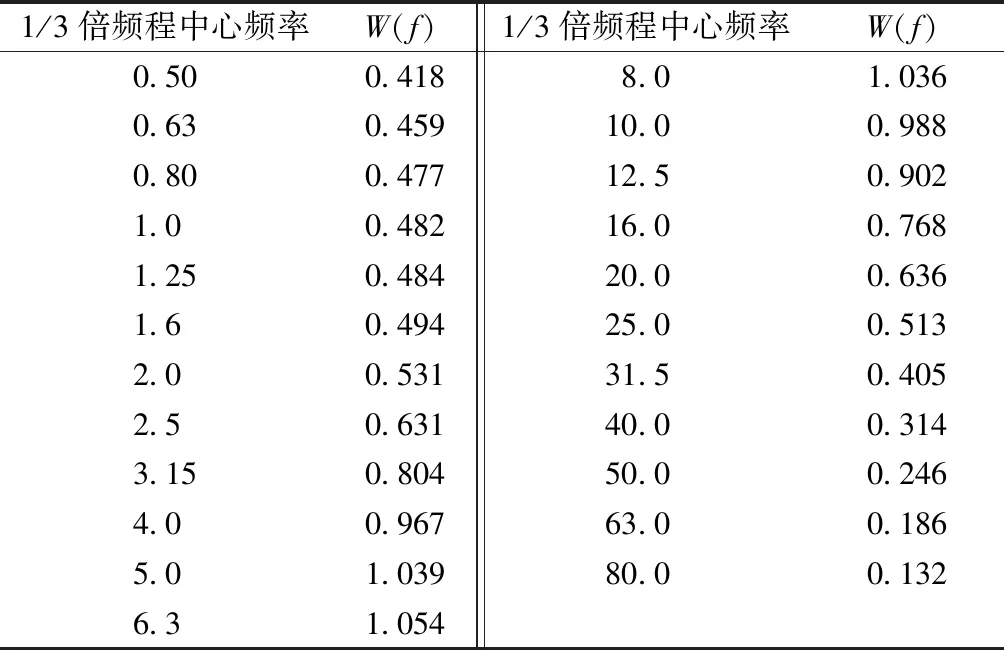
表3 频率加权系数

图6 20 km/h驾驶员座椅处垂直振动加速度
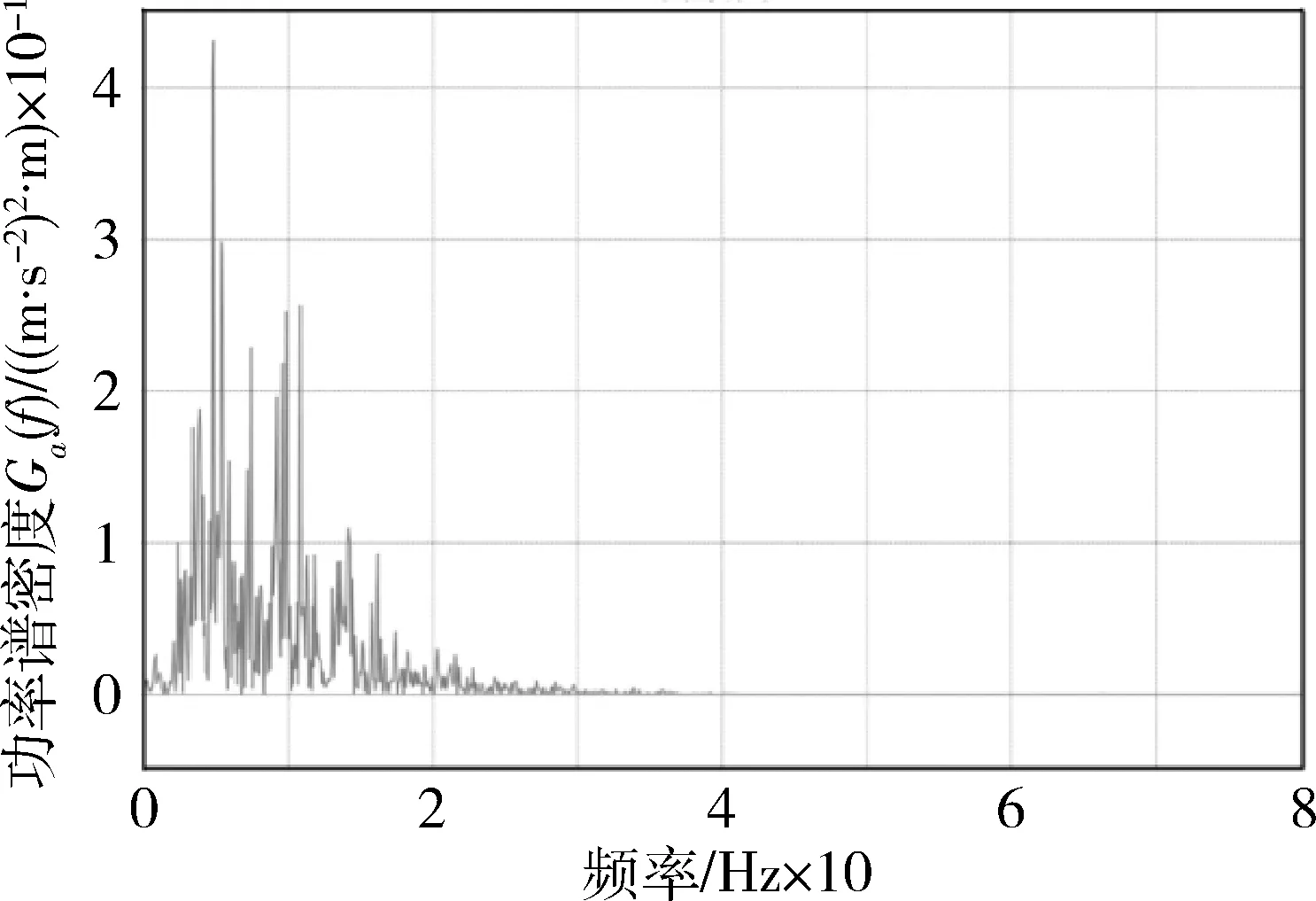
图7 20 km/h加速度功率谱密度
求得驾驶员座椅处垂直方向加权加速度均方根值如表4所示.

表4 驾驶员座椅处垂直方向加权加速度均方根值
通过对比可以看出,采用10%车重为履带预紧力时的车辆驾驶员座椅处垂直振动加权加速度均方根值小,平顺性较好.因此,从平顺性最优的角度出发,该型履带车辆的履带预张紧力取10%左右较合适.
4 结束语
以某型高速履带车为例,在多体动力学仿真软件RecurDyn中建立了整车动力学模型,在不同车速下分别取车重的6%、8%、10%、12%为履带预张紧力对车辆平顺性进行了仿真.通过对比可以看出,从平顺性最优的角度出发,该履带车履带预张紧力取10%左右较合适.
