动力总成悬置系统刚度优化研究

2019-05-14刘勺华邵亭亭路纪雷

重庆交通大学学报(自然科学版) 2019年5期

刘勺华，邵亭亭，路纪雷

(1. 常州机电职业技术学院车辆工程学院，江苏常州 213164； 2. 南京徐工汽车技术中心，江苏南京 210012)

0 引言

动力总成系统是汽车的重要组成部分之一。但随着汽车工业发展，汽车速度逐渐提高，重量逐渐减轻，使得车辆振动问题变得日益突出。发动机在工作过程中产生不平衡力和力矩与路面不平度是汽车振动的主要激励源[1]。

发动机作为汽车最重要的振源之一，其产生的振动若得不到很好控制，则会引起车身部件、车架以及与车架相连的其他零件异常振动和噪声。一方面会降低这些重要部件的疲劳寿命，另一方面剧烈的振动使驾乘人员产生不舒服和疲惫感，对汽车平顺性的主观评价造成严重负面影响。

因此如何通过设计性能良好的动力总成悬置系统，以减少动力总成向车架及车身振动能量传递，一直是车辆设计师们关注的重要课题。自动力总成悬置系统能量解耦方法提出后得到极大推广，成为设计师们解决此问题最重要方法之一[2-3]。

笔者利用能量解耦方法，借助动力学分析软件ADAMS建立了由潍柴发动机及法士特变速箱组成的动力总成悬置系统模型，从能量法角度出发对悬置刚度进行匹配优化，取得了较好结果。

1 动力总成悬置系统

1.1 动力总成悬置系统简化建模

动力总成悬置系统固有频率远远小于动力总成弹性模态频率，因此在对悬置系统进行研究时常将动力总成和车架假定为刚体。用于发动机和车架连接的橡胶悬置，由于阻尼不大，且动力总成是小幅振动，因此建模时其阻尼予以忽略；悬置的3向刚度则用3个相互垂直的弹簧连接表示，这3条轴线为弹性主轴[4]。

此外，建立模型时需建立几个坐标系：① 定坐标系G0-XYZ，原点G0位于动力总成静平衡时的质心；Z轴平行于曲轴轴线，指向发动机前方；Y轴垂直于曲轴方向向上；X轴按右手定则确定。② 动坐标系GXYZ，原点G固结在动力总成质心处，静平衡时动、定坐标系重合。动力总成刚体振动是由动坐标系相对于定坐标系平动和绕3个坐标轴转动合成。因此广义坐标为X、Y、Z、θx、θy、θz[5-6]。

基于此，动力总成悬置系统简化力学模型和ADAMS模型分别如图1。发动机为4点悬置，前后各2点，变速箱前面与发动机后部螺栓连接，后面为1点悬置，每个点为3自由度，故动力总成悬置系统模型共15自由度。

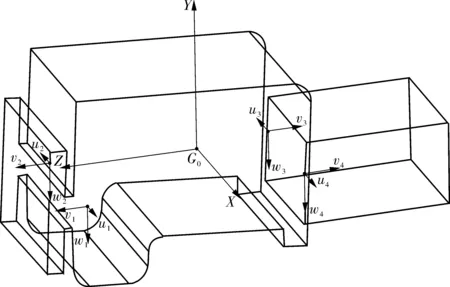
图1 动力总成悬置系统力学模型

1.2 变速箱弹性支撑刚度

发动机悬置的3向刚度一般可从悬置供应商处直接获得，但变速箱弹性支撑——扁担梁则需要通过一定技术手段获取。笔者采用柔性体建模方法获得扁担梁刚度曲线，图2为扁担梁3D模型。

图2 扁担梁3D模型

图3 模态垂直振动

采用柔性体方法获取刚度曲线具体步骤为：将3D模型导入有限元分析软件，划分网格、定义外连接点、设置模态信息，将模型导出mnf柔性体文件，最后将柔性体文件导入ADAMS添加约束及载荷，查看刚度曲线。

扁担梁柔性体前3阶模态如图3。前3阶模态频率分别为83、117、241 Hz。由图3可看出：扁担梁前3阶柔性体模态振型正对应于总体坐标系Z、Y、X这3向振动。

在扁担梁柔性体相应位置施加X、Y、Z这3个方向力得到力-变形曲线，其斜率即为单向刚度，其X、Y、Z这3个方向刚度分别为：12 000、3 100、1 420 N/mm。

1.3 优化前仿真结果

对模型中各元件赋值，如对于动力总成输入质心位置、转动惯量等参数，各悬置输入初始刚度值。经过ADAMS振动分析求解器Vibration求解得到优化前系统前6阶模态频率及能量占比分布，见表1。

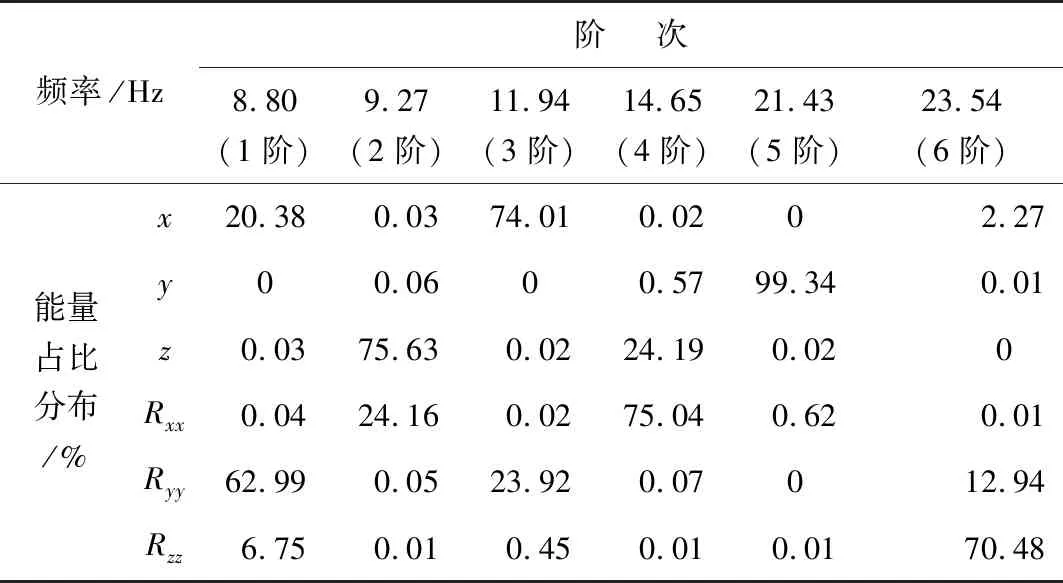
表1 优化前系统频率及能量分布

2 动力总成悬置系统优化

2.1 动力总成悬置系统数学模型

拉格朗日自由振动微分方程如式(1)：

(1)

式中：T为系统动能；Qi为系统广义坐标；V为系统势能。

将系统各参量代入式(1)可得动力总成悬置系统振动微分方程，如式(2)：

(2)

系统自由振动微分方程如式(3)：

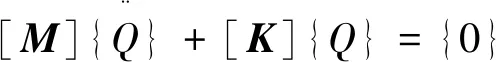
(3)

式中：[M]为系统质量矩阵；[K]为系统刚度矩阵。

2.2 设计变量选择

通过改变系统刚度矩阵K可控制系统振型及固有频率，刚度矩阵是弹性支撑安装位置、角度、刚度的函数。因此可将发动机各悬置点刚度和弹性中心点作为设计变量。

2.3 目标函数

根据振动匹配思想，悬置系统振动解耦关键是各方向上能量占比达到100%，且频率满足最值要求。但在工程实践中，使系统6个自由度方向完全解耦是没有必要的，同时也是很难实现的，故通常都是使几个主要振动方向得到解耦即可。根据一般汽车特点，其激励主要来自于绕发动机曲轴的转动和垂直向上的来自路面激励，因此只需使Y方向和Rzz方向解耦即可。