基于水平应变监测信息的边坡稳定性评价研究
2019-05-14唐胜传黄诗渊周泳峰
唐胜传,黄诗渊,周泳峰
(1.招商局重庆交通科研设计院有限公司 山区道路工程与防灾减灾技术国家地方联合工程实验室, 重庆 400067; 2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074)
0 引 言
随着我国经济的快速发展,大量的基础建设工程建设于西部山区,由于山区的特殊性,许多基础工程需坐落于边坡上。在边坡上建立地基可能被认为是一种边坡稳定性或承载力问题[1-2],其破坏模式受到岩体体类型[3-6],边坡几何[7-8],地基类型,地基位置[9-10],基础宽度及荷载大小[11]的影响。由于边坡与地基的相互作用,边坡在附加荷载作用下的稳定性评价成为地质工程师的一项重要任务 。
目前,现场监测是防治边坡失稳破坏的一个主要手段,实时监测数据能够给边坡的安全稳定评价提供数据支持,是工程预警的重要支撑。 由于影响边坡安全的因素较为复杂,边坡岩土体的力学参数和安全状态难以确定,需要设置各种监测仪器对边坡的岩土体进行精细的监测,实现对边坡安全状态发展变化的监测。
传统的边坡监测方法主要是对地表位移进行监测,但对边坡稳定性评价充满了不确定性[12-13]。近年来,随着分布式光纤传感技术的迅速发展,一种新的监测方法逐渐在各种工程边坡和滑坡中得到应用,通过实时监测边坡的应变分布信息进而对边坡实时状态进行评价[14]。相对位移而言,应力、应变的累积更能够表征边坡劣化过程,根据应变监测结果,就有可能重构边坡内部应变场,就有望对坡体内部滑动面的进行预测并实现边坡失稳过程的评价。
学者们[14-15]对一均质土坡条形荷载作用下的应变分布进行了研究,发现稳定性系数与不同高程的最大水平应变之间的关系可用幂函数表示,为边坡的早期预警和稳定性评价提供了新的思路。然而,其仅讨论了基础坡顶距为0 m时的情况,需要进一步的深入探讨。
基于此,建立了几种不同情况下的边坡,研究了边坡在条形荷载作用下失稳过程中水平应变的分布情况,对稳定性系数与水平应变之间的关系进行了讨论分析,并对分布式光纤传感监测布置位置进行了建议。
1 数值模型
采用有限元软件MIDAS-GTS NX,建立了3种均质边坡模型,其中,边坡高度H=15 m,坡角β=45°,条形基础宽度B=6 m,仅改变条形基础的坡顶距D,分别为0、4、14 m,数值模型如图1。
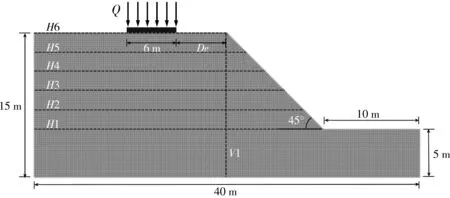
图1 数值模型
模型网格的大小设置为0.2 m,底部约束水平和竖直位移,两侧约束水平位移。土体材料参数见表1,采用摩尔库伦破坏准则。在数值计算中,条形基础的均布荷载按线性增加,直至计算不收敛,此时可认为已发生破坏。同时,用规范常用的Bishop法计算了边坡在不同荷载作用下的稳定系数。

表1 土体力学参数
为了监测在破坏过程中边坡的实时信息,于不同高程建立了6条水平应变监测线,标记为H1~H6。同时,为模拟传统测斜仪,建立了垂直位移监测线设置为获得位移数据,标记为V1。
2 结果与分析
2.1 加载过程中的水平应变分布
对坡顶距D=0 m的边坡模型进行分析,得到了边坡内部水平应变的分布,如图2。由图2可知:在加载刚开始时,最大拉应变出现于坡脚处,而基础与边坡接触区域承受压应变,在基础下部较深区域,水平应变主要体现为拉应变。随着堆载的增加,坡脚处的应变集中逐渐向内发展,地基下的应变集中区逐渐发展成倒三角形。当荷载达到80 kPa时(此时地基已发生破坏),水平拉应变集中区与和边坡潜在滑移面相交,如图2(c)。
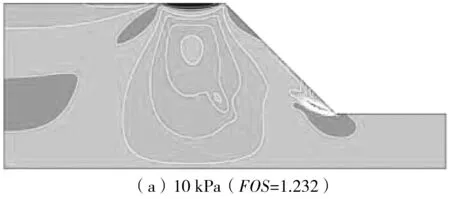

图2 加载过程中水平应变云图(拉为正,压为负)
2.2 不同高度下的水平应变分布
为了研究边坡在加载过程中的应变状态,得到了各高程的水平应变分布,如图3。
由图3可见:对于H6测线,基础位置处的的水平应变主要体现为压应变,当荷载达到80 kPa时,基础左侧主要体现为拉应变,最大拉应变出现于基础的左端,符合地基的破坏的一般模式。在实际工程中,该拉应变突变可预测坡顶拉裂缝的形成。而对于H5~H1测线,基础以下的水平应变主要体现为拉应变,当荷载较小时,最大水平应变随荷载增加呈线性增加,而当荷载大于60 kPa后,最大水平应变随荷载增加呈非线性增加。
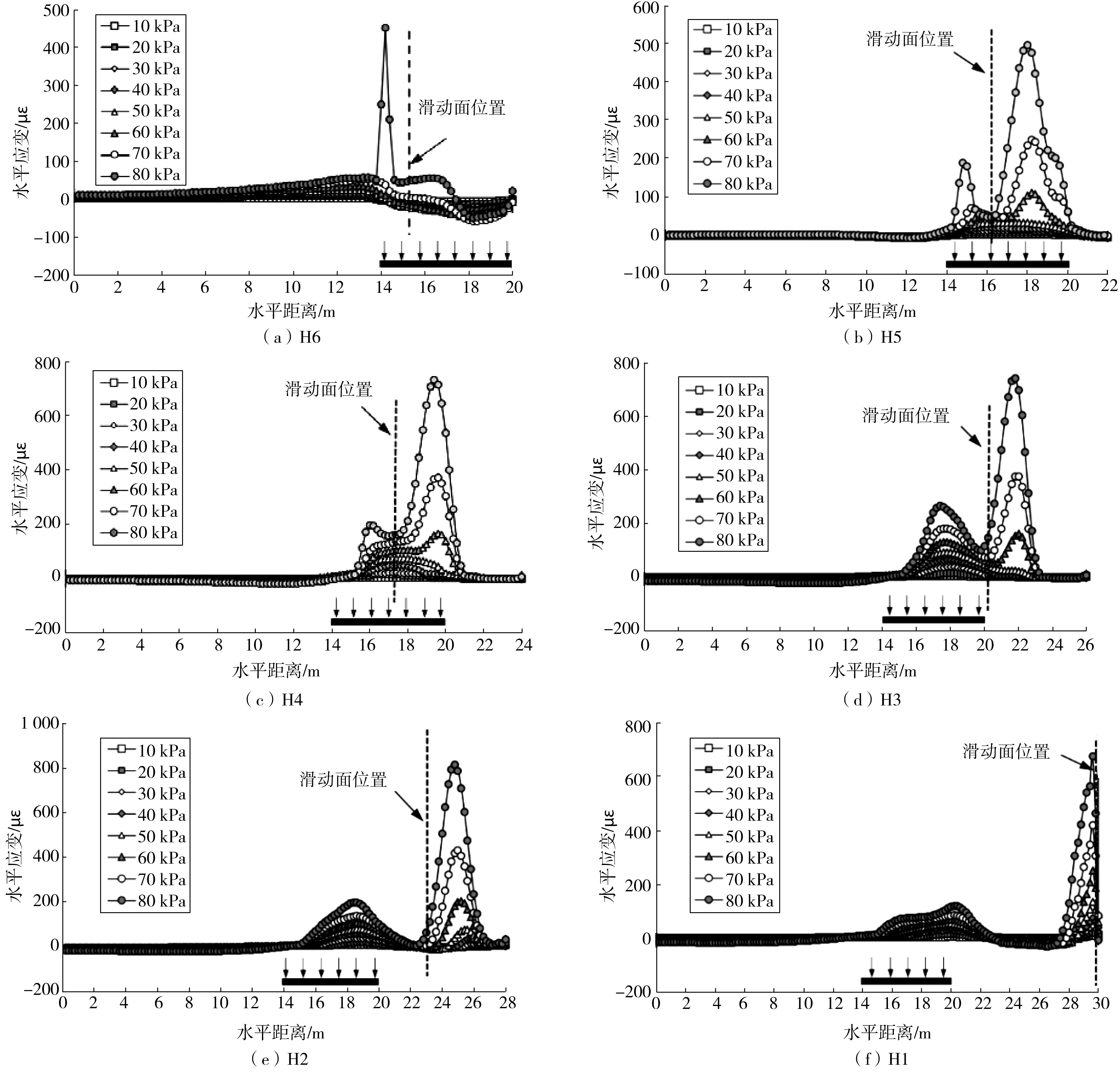

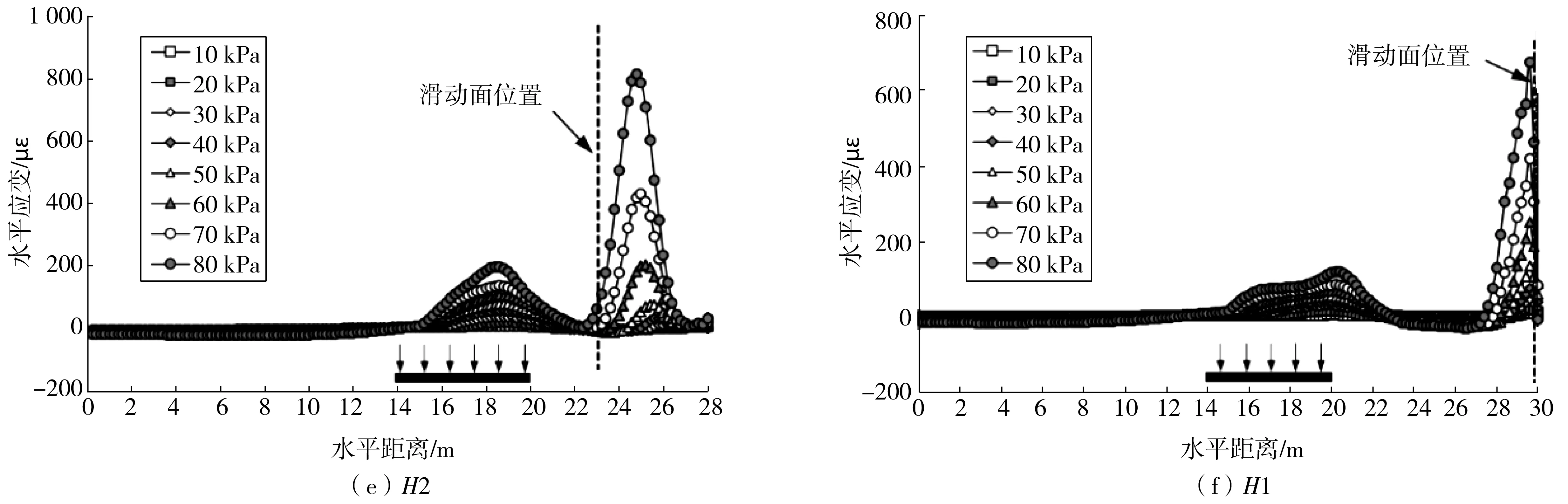
图3 加载过程中边坡不同高程处水平应变分布
通过对6条监测线中的水平应变分布进行比较,发现随着高度的降低,最大水平应变出现位置逐渐向右移动,最大水平应变值出现于测线H2中。采用Bishop法计算得到的潜在滑动面与各测线的交点处的水平应变并不是该测线上的最大水平应变,说明在条形基础荷载作用下,水平测线监测到的最大水平应变出现的位置并不能准确获取潜在滑动面位置,不过,应变分布可以反映实际土体的局部应力状态。
为了比较位移,V1监测线中水平位移的分布如图4。研究发现:随着基础荷载的增加,最大水平位移呈非线性增长,而且最大水平位移出现的位置逐渐上移。最终,当地基发生破坏时,最大水平位移约为15 mm。此外,垂直测线V1 上的水平位移最大值并不能预测滑动面位置,滑面上方土体质点的水平位移一般都比滑面上质点的水平位移更大。

图4 加载过程中不同高程的水平位移分布
2.3 水平应变和稳定性系数关系曲线
文献[15]的物理试验结果表明,水平应变与稳定性系数之间有很好的拟合关系,其可以用对数曲线拟合,如式(1):
F=mln(ε)+n
(1)
式中:F为边坡的稳定性系数,是各监测线的最大水平应变;m和n为拟合公式的常数无量纲参数;ε为各测线的水平应变最大值。
根据式(1)将边坡模型(D=0)的数据进行拟合,如图5,可见所有相关系数均大于0.9,其中H1监测线的应变参数具有最佳的拟合效果。因此说明,在实时现场监测中利用应变参数评价这种稳定性是可行的。
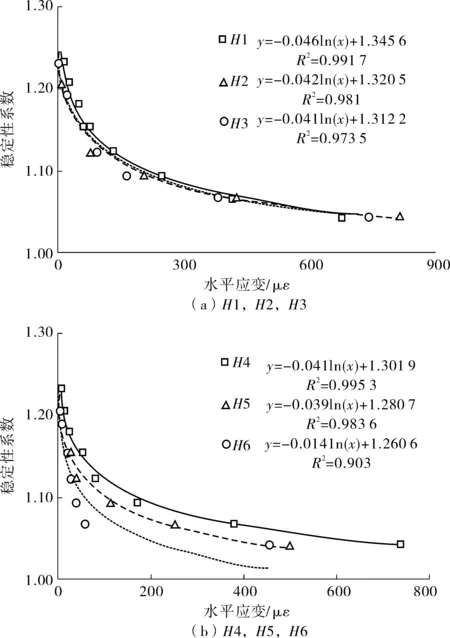
图5 水平应变与边坡稳定性系数的关系
2.4 基于水平应变评价边坡稳定性
在工程实践中,由于经济问题,光纤传感器并不可能安装在边坡内部的各个部位,它应安装在边坡在最关键的位置(通常在边坡内部区域)进行实时监控。在边坡数值分析中,土体的塑性区通常以增量的形式表示,因此,将各测线最大水平应变换成增量的形式,作出其与边坡稳定系数之间的关系,见图6。
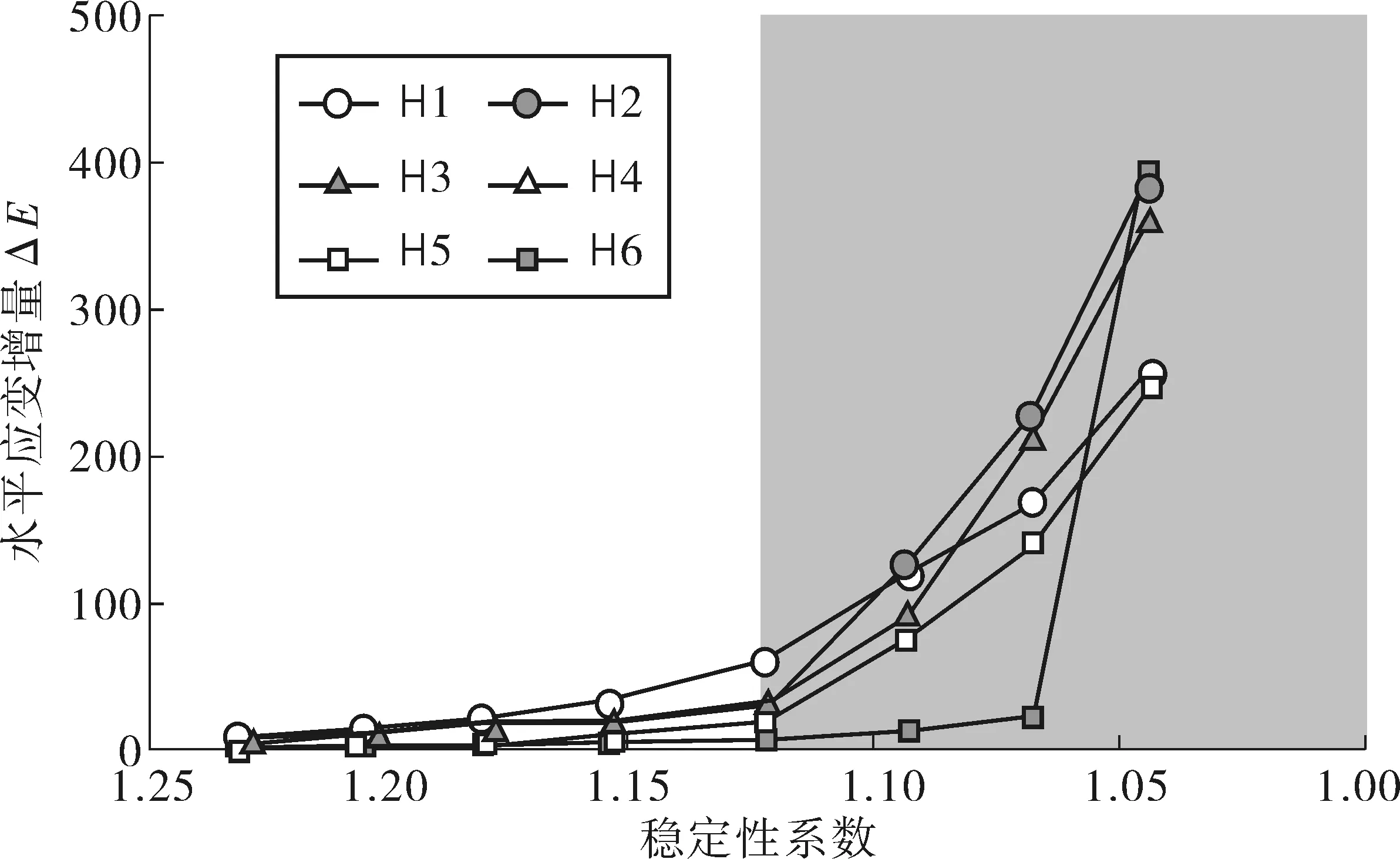
图6 水平应变增量与边坡稳定性系数的关系曲线
由图6可见,在荷载逐步增加的过程中,边坡的稳定性逐渐降低,应变增量逐步增长,当稳定性系数降低到一定水平时(F=1.125)时,测线最大应变增量发生突变,如图6的灰色区域。因此,利用各水平测线的应变信息对边坡的稳定性进行预测是可能的,当水平应变增量增速较大时,标志着边坡有失稳的危险。
3 讨 论
以上分析结果说明式(1)的拟合关系适用于条形基础下均质边坡的稳定性评价。但文献[15]和前文仅仅对坡顶距D=0时的边坡进行了分析,为了验证该关系是否适用于其它情况,构建了另外2个模型,其坡顶距D分别为4、14 m,土体参数保持一致。首先,按照式(1)对以上两种坡顶距的模型进行数据拟合,如图7。对于D=4 m时的边坡模型,各测线的最大水平位移与稳定性系数对数函数拟合关系良好,相关系数均在0.89以上,然而,对于D=14 m时的边坡模型,各测线的最大水平位移与稳定性系数的对数函数拟合关系较差,最大相关系数仅仅为0.485。因此,可以说明,当坡顶距较大时,对数函数关系不再适用。
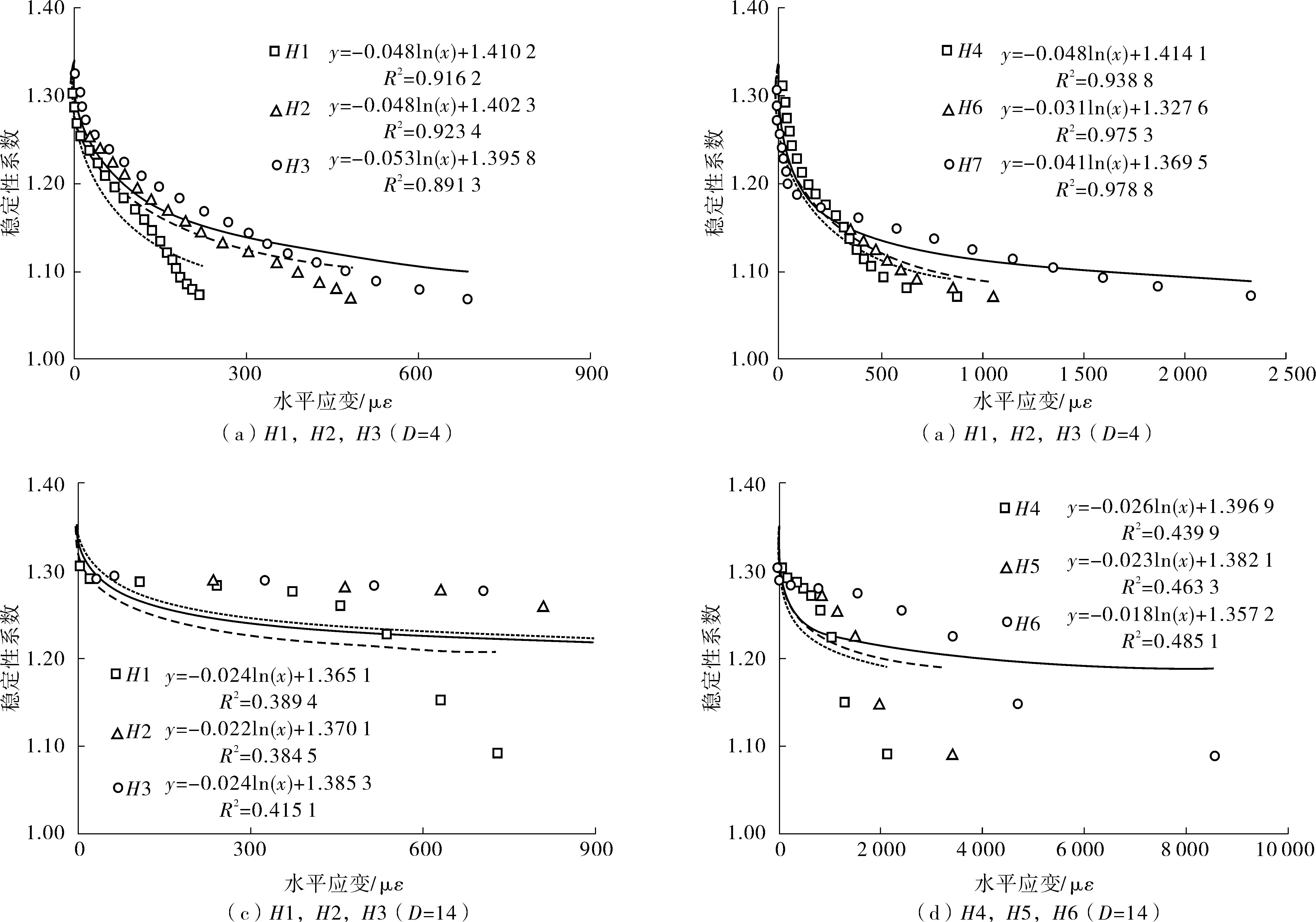
图7 稳定性系数与水平应变的对数关系
图7中显示的关系可以用线性拟合表示,如式(2):
F=aε+b
(2)
式中:F为边坡模型的稳定因子,是各监测线的最大水平应变;a和b为拟合公式的常数无量纲参数。
如图8,所有的相关系数均在0.76以上,对比而言,测线高程越大,其拟合关系越好。
条形基础下均质边坡的破坏机理强烈地依赖于荷载的大小和地基的位置[1-2]。当位置发生改变,失效机制发生变化,导致最大应变与稳定因子之间的关系发生变化。当条形基础靠近坡肩时,幂函数和对数函数能够较好地拟合,然而,当条形基础远离坡顶时,线性函数能够较好地拟合。
综合比较以上3种模型中不同测线最大水平应变与稳定性系数的相关系数,如图9。明显地,测线H4和H5相对于其余测线具有更好匹配程度,表明这些区域更适合于边坡应变实时监测,因此,建议在边坡的中上部进行监测。

图8 水平应变与边坡稳定性系数的线性关系(D=14 m)
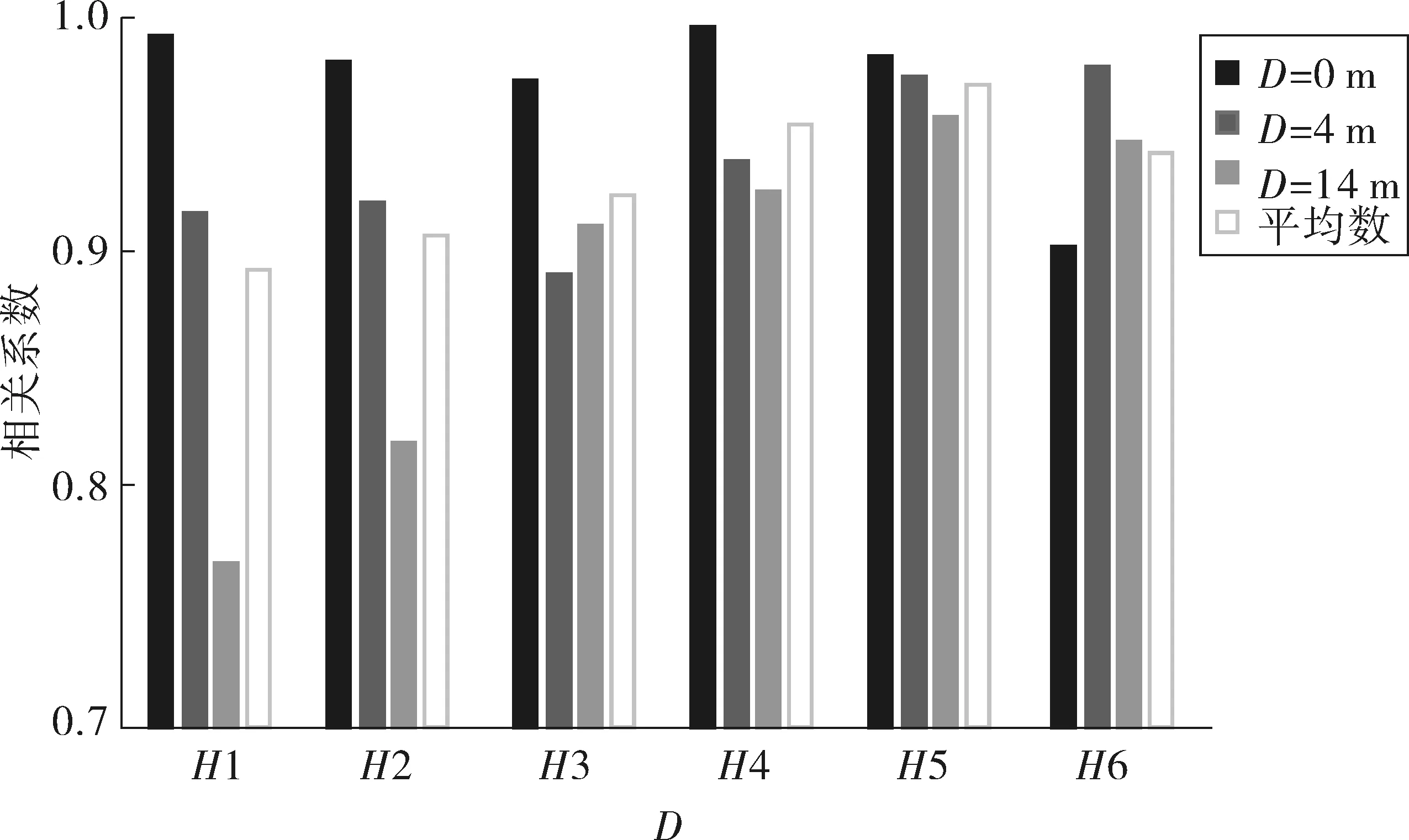
图9 不同测线处水平应变与边坡稳定性系数拟合曲线相关系数比较
5 结 论
笔者通过建立3种不同坡顶的边坡数值模型,进一步的讨论了基于应变的稳定性评价方法。得到以下结论:
1)随着基础荷载的逐渐增加,土体的水平应变也逐渐增加,但最大水平应变和最大水平位移出现位置并非出现于滑动面上,不过,通过水平应变分布可以观察土体的局部应力状态;
2)建立了边坡稳定性系数与测线最大水平应变之间的拟合关系,同时,根据水平应变增量变化趋势可对边坡稳定性进行定性评价;
2)条形基础下均质边坡的破坏机理强烈地依赖于荷载的大小和地基的位置。当故障发生时,失效机制发生变化,导致最大应变与稳定因子之间的关系发生变化。当条形基础靠近坡肩时,幂函数和对数函数能够较好地拟合,然而,当条形基础远离坡顶时,线性函数能够较好地拟合;
3)综合比较不同坡顶距的边坡模型中不同测线最大水平应变与稳定性系数的相关系数,发现最佳监测区域在边坡的中上部,此外,安装于坡顶的光纤传感器也是必要的,有利于监测坡顶的张拉裂缝。
