虚拟正畸治疗中的错位牙齿自动排列方法

李占利，付敬鼎，李洪安，周 康，惠巧娟



虚拟正畸治疗中的错位牙齿自动排列方法

李占利1，付敬鼎1，李洪安1，周 康1，惠巧娟2

(1. 西安科技大学计算机科学与技术学院，陕西 西安 710054； 2. 中国矿业大学银川学院机电动力与信息工程系，宁夏 银川 750021)

针对虚拟正畸技术中人工排牙效率低下问题，提出一种基于拟合优化的错位牙齿自动排列方法。对输入的牙列模型建立排牙坐标系，定义单颗牙齿特征点并建立牙齿局部坐标系。在此基础上，从低维角度分析牙列中各颗牙齿的位置和姿态，采用加权拟合优化的方法分别计算牙齿的坐标平移量与局部坐标轴旋转量，形成牙齿位姿与空间牙列曲线的关联约束，并结合矩形包围盒的碰撞检测方法，设计基于最速下降法的迭代算法在空间牙列曲线约束范围内调整牙齿位姿，完成牙齿的自动排列。实验结果表明，排好的牙列与人工排牙结果相差无异，排牙效率大大提高；与现有排牙方法相比，更贴近临床牙齿矫治，且牙齿移动代价总量明显降低。

虚拟正畸；自动排牙；加权拟合；优化

拥有一副整齐洁白的牙齿，能够令人更加自信，迎合现代人爱美的生活观念，牙齿健康逐渐受到人们重视。计算机辅助设计(computer aided design，CAD)与口腔医学的交叉融合，使得虚拟牙齿矫治技术[1-2]成为研究热点。牙齿排列是牙齿矫治的关键技术之一，运用计算机技术对牙齿数字模型进行排列，一方面，分析三维空间中各颗牙齿的正畸移动方向能够作为医生制定治疗计划的参考，另一方面，将数字化三维牙齿模型的排列过程进行可视化展示，可以让患者预先了解矫治结果[3]，因此，研究牙齿排列过程具有重要意义。

传统上，牙齿排列工作由人工完成。MOTOHASHI和KURODA[4]于1999年提出将数字化牙颌按单颗牙齿分离，并采用人工的方式完成排牙。人工排牙虽然能够达到正畸治疗的要求，但效率很低，通常的做法是定义排牙坐标系与牙齿局部坐标系，并根据临床经验对错颌牙列生成一条牙弓线作为辅助，人为地将上下颌的牙齿牵引至牙弓线附近。此过程让一位训练有素的排牙技师操作，大约需要15~20 min，而且还会存在视觉误差影响排牙结果，由此可见，实现自动排牙十分有必要。

目前，CAD自动排牙技术已有诸多研究成果，自动排牙实质是先预测每颗牙齿的位置和姿态，然后将牙齿从初始位姿移动到预测位姿的过程[5]。研究可分为错颌正畸[6-8]和个性化义齿排牙[9-13]两种。错颌正畸是根据上下牙颌模型建立咬合面，及上下颌牙弓线，再将牙齿在局部范围内迭代调整；义齿排牙则是打破现有牙列咬合平衡状态，重组牙列，其需要建立符合患者实际情况的参考平面或参考线作为排牙依据，通常是根据患者颅骨数字模型建立咬合面和牙弓线。相比较之下，错颌正畸方法的时间复杂度虽然比义齿排牙方法高，但对于所有牙齿从初始位置移至目标位置的移动总量而言，前者方法更有优势，因为牙齿移动总量越少意味着正畸治疗周期越短。

上述，无论哪种研究方法都需要建立排牙参考平面或曲线。本文结合两种研究思路的优势，提出一种基于拟合优化的错位牙齿自动排列方法。该方法无需人工操作生成咬合平面、牙弓线等作为排牙参考，可以将错颌牙列的光固化成型(STereoLithography，STL)数字模型快速排列整齐，提高排牙效率。实验部分对本文方法进行验证，展示了多组排牙结果，并与义齿排牙方法、专家人工排牙结果进行对比。

1 相关工作

在错颌正畸方面，ALAN等[5]提出通过在每颗牙齿近远中面上选取合适的特征线段，将选取的线段按照牙齿在牙弓线上的顺序依次逼近牙弓线并牵引牙齿移动，以实现半自动排牙。王先泽等[6]提出一种基于粒子群优化算法 (particle swarm optimization，PSO)的自动化排牙方法，将单颌的各颗牙齿特征点到该颌的牙弓线最短距离之和作为目标函数，再结合PSO算法求解出牙齿正畸最终位置。KUMAR等[7]充分使用了牙齿表面特征，如牙尖、边缘嵴等，定义牙列咬合关系、颊舌向倾斜度、牙列边缘对齐等7项约束特征，并建立约束模型图，以单颗牙齿为质点、约束为弹簧，建立弹簧质点模型，将上下颌牙齿逐步校正至近似最佳的咬合；但该方法采用了美国正畸学会公布的客观评分系统[14](ABO-OGS)作为算法迭代依据，该评分系统均采用整数计分制，因此导致迭代次数过多，算法运行时间长。

在义齿排牙方面，文献[9-11]提出一系列关于机器人义齿排牙方法，采用幂函数作为牙弓线数学模型，利用牙宽迭代计算各颗牙齿在牙弓线上的摆放位置，分析应对患者不同错颌类型时将颌平面、牙弓线做出相应调整。SUN等[12]提出利用CAD和快速成型(rapid prototyping，RP)技术辅助制作可摘全口义齿的方法，包括牙齿和牙龈个性化设计、自动排牙。文献[13]介绍了一款个性化的排牙系统，该系统操作对象包括颅骨数字模型、具有牙根的牙齿数字模型等，根据颅骨模型与牙齿模型计算上下颌骨对颅底，上下颌骨之间的矢状位置关系[15]，从而建立咬合面和牙弓线，并采用与文献[9]类似的方法进行排牙，但该系统在部分排牙步骤中仍需要手动调整，不完全是自动排牙。

2 自动排牙算法设计

本文研究对象是牙颌STL数字模型按单颗牙齿分离后的牙冠数据，分离时保留各颗牙齿的相对位置信息[16]。本文采用世界牙科联盟(Fédération dentaire internationale，FDI)牙位表示法对牙齿进行编号，从观察者角度看，上颌左侧从中切牙起至第三磨牙编号为11~18，上颌右侧编号为21~28，下颌右侧编号为31~38，下颌左侧编号为41~48。图1展示了分牙后的上颌牙列数据。

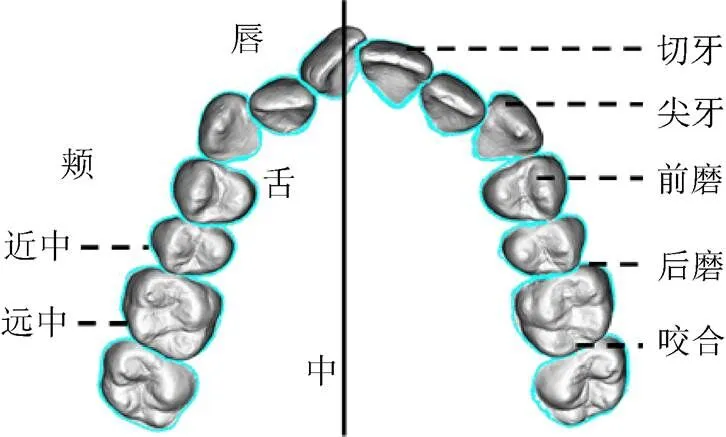
图1 上颌牙列数据

2.1 技术准备

2.1.1 排牙坐标系

建立排牙参考坐标系是排牙的前提条件之一，但建立坐标系的方式不唯一，依然以观察者的角度，按照如下步骤建立排牙坐标系：①确定坐标原点，在中线靠近嘴唇的位置，且原点落在咬合面上；②坐标轴垂直咬合面，方向指向上唇、人中、鼻尖及眉间点；③坐标轴与假想的中线平行，经过上颌切牙的切缘，与左右两侧的第一磨牙近中颊尖点连线垂直；④坐标轴在上颌切牙的切缘方向，指向观察者的右侧。如图2所示，3个坐标轴符合右手定则。

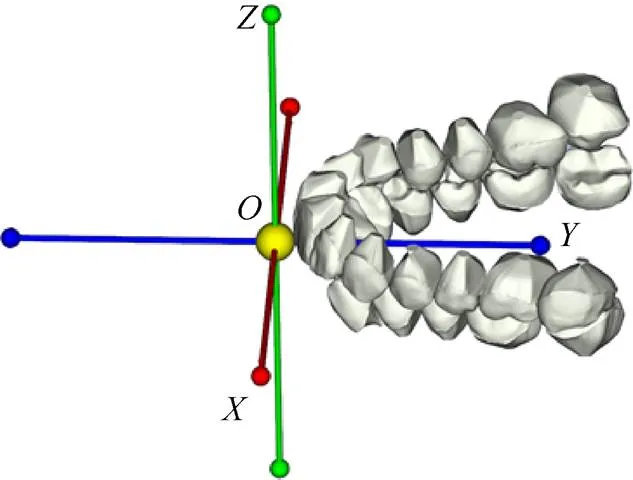
图2 排牙坐标系

2.1.2 牙齿局部坐标系

本文采用通过特征点建立牙齿局部坐标系的方法。特征点通常是一个区域与另一个区域的边界，且特征点处的曲率变化较大。结合牙齿解剖学对人类牙齿特征的描述，牙齿的表面特征点通常定义在相邻牙齿牙冠的接触点、牙体各轴面的外形高点以及牙齿突出尖点。

图3展示了切牙、尖牙、前磨牙、磨牙4种类型牙冠数据特征点。以前磨牙为例，在牙齿模型质心处建立局部坐标系。定义颊侧尖点名称为、舌侧尖点名称为、牙槽沟近中侧缘点名称为、牙槽沟远中侧缘点名称为。以两点连线方向为坐标系的轴方向，正方向由颊侧指向舌侧；再将两点相连，以和叉积的直线方向为坐标系的轴方向，正方向为咬合方向；最后以轴和轴叉积的直线方向为坐标系的轴方向。图4展示了前磨牙的局部坐标系，该坐标系为右手坐标系。

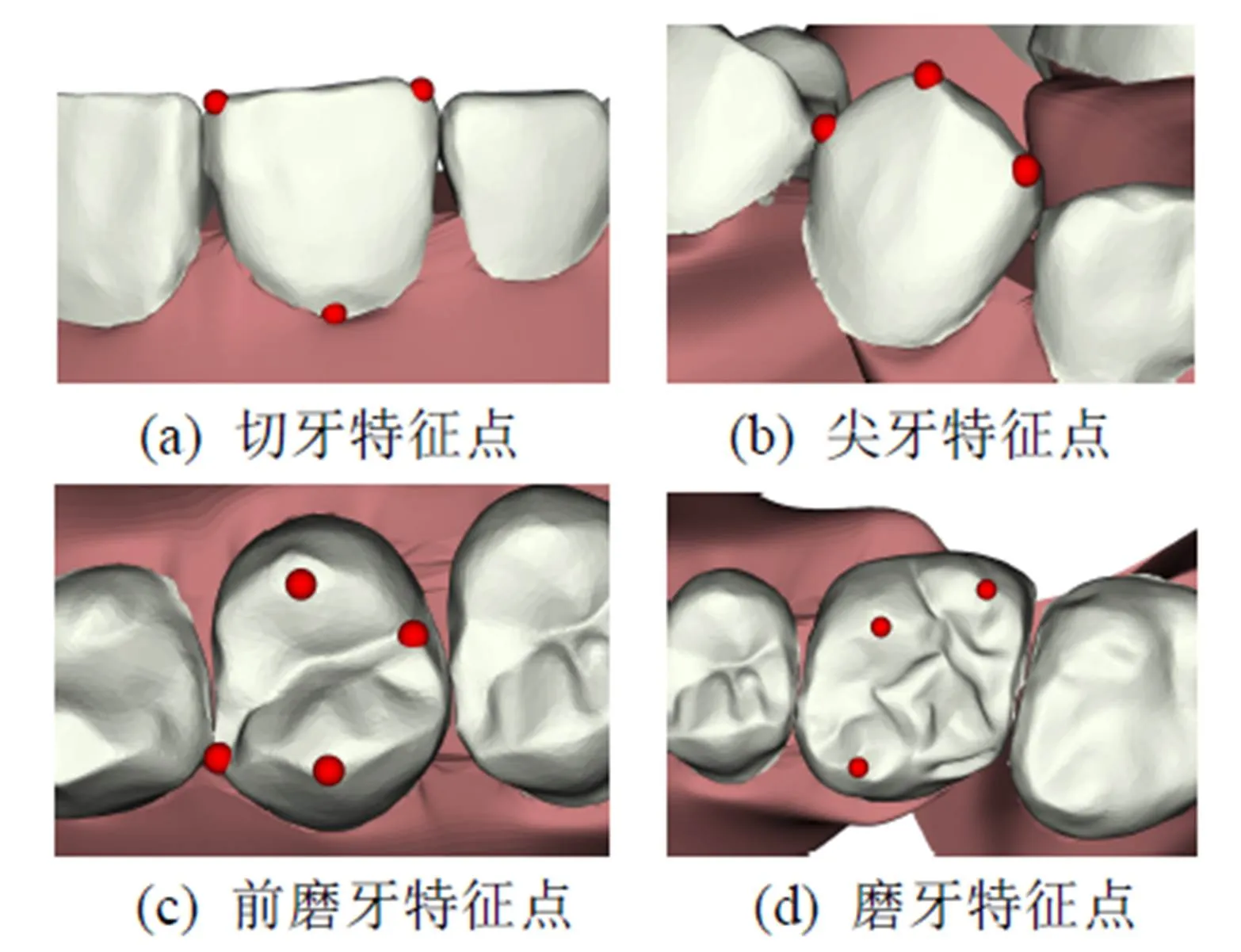
图3 牙齿特征点

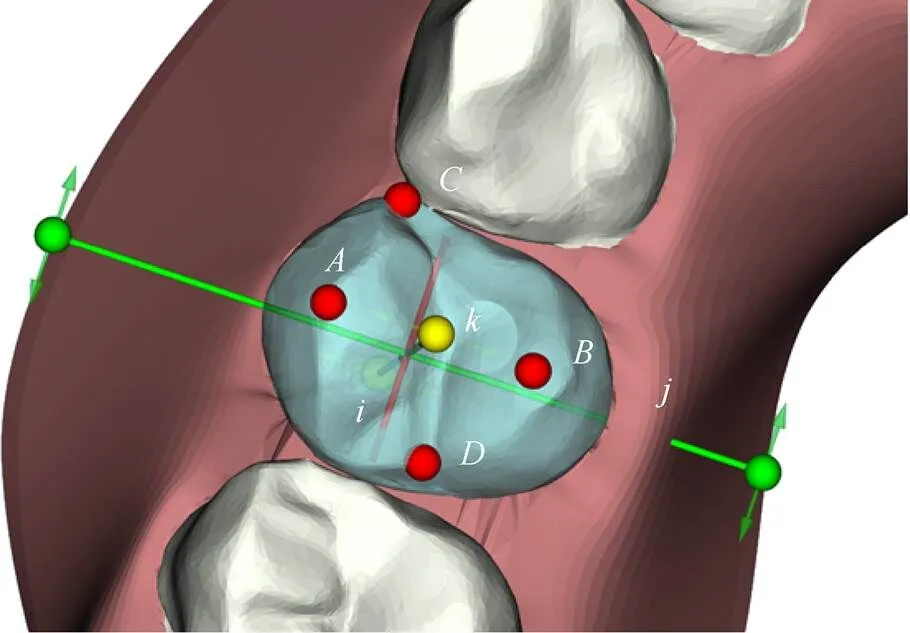
图4 牙齿局部坐标系

2.1.3 坐标转换

假设单颗牙齿不会发生磨损与形变，可视其为刚体，更深入的研究可以考虑上下颌咬合导致的牙齿微小变形。单颗牙齿在三维空间中可表示为点集{T}(=1,2,···,,≥4)，在本文排牙算法中记为{T}，其中为牙号。刚体在空间中自由度为6，可设单颗牙齿T上任意一点在排牙坐标系的位置为(,,)，建立三维空间下单颗牙齿局部坐标系为,,,，如图5所示。

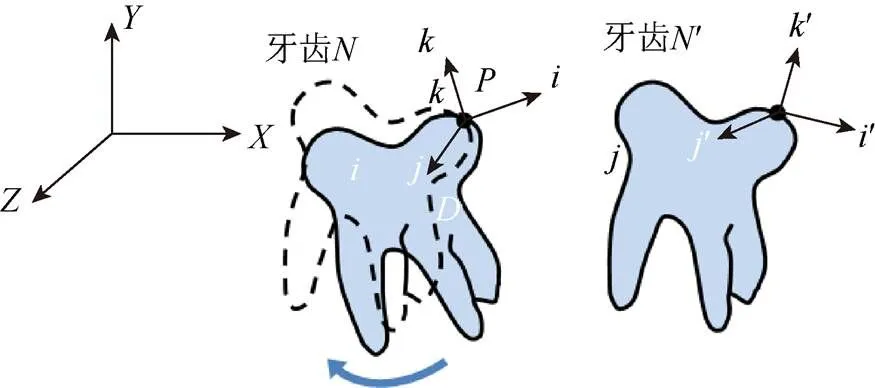
图5 牙齿移动示意图

文献[17]研究了刚体移动过程中发生形变与不发生形变的2种情形，分别求解出2种情形下式(1)的仿射变换矩阵，其中发生形变时，仿射变换矩阵必不是正交矩阵，此时可将旋转矩阵用一个近似的正交矩阵代替。牙齿初始任意位姿，经任意平移旋转变换为牙齿ʹ，任意点处坐标(,,)经变换得(ʹ,ʹ,ʹ)，局部坐标系向量{,,}经变换得{ʹ,ʹ,ʹ}，且2个几何体恒等，有正交变换为

值得注意的是，任意平移旋转都可以拆成3个欧拉角构造旋转矩阵，但绕轴旋转的顺序不唯一，因此构造旋转矩阵的方式也不唯一。

2.2 拟合优化

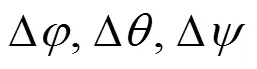
图6 空间牙列曲线示意图

2.2.1 平移量

结合2.1.2节的叙述，分别对上下颌取切牙切缘两特征点的中点、尖牙的尖点、前磨牙的颊侧尖点、磨牙的颊侧两特征点的中点，记为P(为牙号)，可得到点集{P}。

对于平移量Δ，Δ，计算思路如下：选定拟合函数模型，通过得到的投影点集{P}⊥拟合得到曲线表达式，再计算各投影点到拟合曲线的最短距离即为平移量Δ，Δ。许多专家研究了人类牙弓线数学模型，观点不一，主要有椭圆线函数、垂链线函数、多项式函数、三次样条函数、幂函数、Beta方程[19]等。本文选用Beta方程作为拟合函数模型

其中，为牙弓深度；为牙弓宽度；参数可通过尖牙位置求得，即：在，确定后，将(2-1/2,1+2/2)坐标代入式(2)中求出值，(1,1)，(2,2)分别为单颌左右两侧尖牙的特征点在横断面上的投影坐标，式(2)中参数可取=42.512 mm，=57.923 mm，=1.921。

选定函数模型之后，利用最小二乘法求解拟合曲线解析式，考虑到在实际正畸治疗中，后牙的移动量远小于前牙，因此为每颗牙齿加权，得到如下表达式

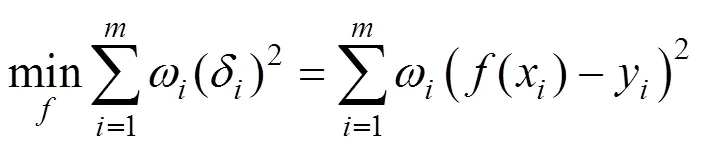
其中，()为选取的函数模型；为权值；为单颌牙齿数量。通过式(2)拟合投影点集{P}⊥得到函数模型参数，绘制函数图像如图7所示，从图中可以看出，后牙特征点几乎分布在曲线上，这是由于为后牙赋的权值相对前牙较高，符合后牙正畸移动相对困难的实际。图7(a)以Beta函数为模型拟合上下颌牙齿特征点在横断面投影点，其中下颌拟合曲线比上颌缩进一些。计算各投影点到拟合曲线的最短距离，即

联立曲线解析式()求得平移量Δ，Δ。值得注意的是，按照上述方法计算得出的平移量并非排牙最终结果，后叙基于碰撞检测的调整算法以空间牙列曲线作为，变量的约束进行迭代调整。

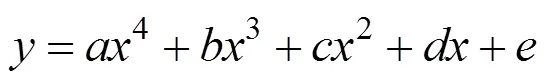
为拟合模型，拟合的数据为单颌牙齿在冠状面的投影点集。求得平移量Δz时需注意，此时牙齿的Δy已确定，因此对图7(b)所示数据作拟合优化时只取点PN在Z轴方向到曲线的最短距离，由曲线解析式z=f(y)即可求得Δz。

2.2.2 旋转量

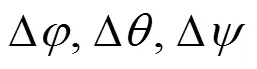
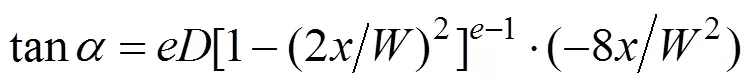
其中，等号右边由式(2)求一阶导数得到，构造出角关于的函数关系式()，以此关系式为函数模型，对单颌每颗牙齿的轴在横断面的投影向量与轴的夹角和牙齿特征点轴坐标进行加权拟合，即

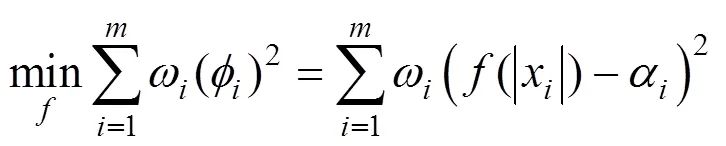
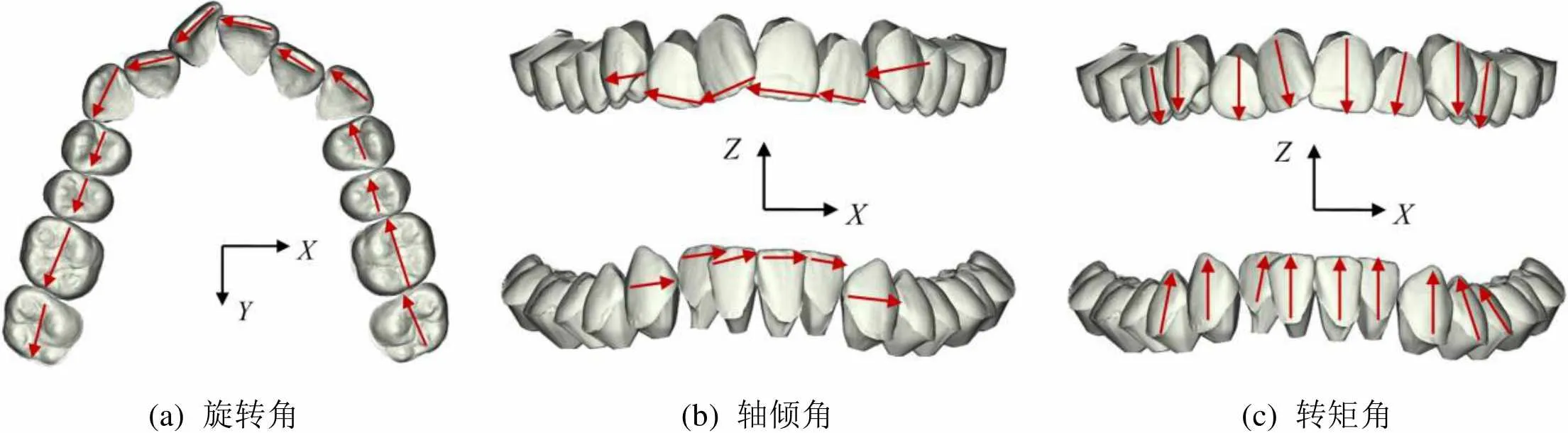
(a) 旋转角(b) 轴倾角(c) 转矩角

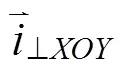
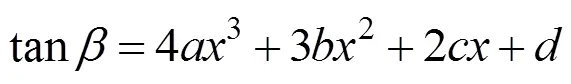
其中，等号右边由式(4)求一阶导数所得。同样采用加权拟合，由式(6)可以得到函数图像如图9(b)所示，图中拟合图像展示了各颗牙齿i轴向量投影与的夹角关于X轴坐标的变化趋势为方便观察，将上颌的夹角取补角，因此上颌拟合曲线一阶导数走势恰好与下颌拟合曲线相反。同样的，由计算得出牙齿绕j轴的旋转量。

2.2.3 碰撞检测与迭代调整

上节采用加权拟合优化的方法对错位牙齿的位置和姿态进行优化调整，得到了各个平移量和旋转量关于排牙坐标的函数关系，相当于将牙齿位姿约束到空间曲线上，但各颗牙齿在空间曲线的具体位置尚不可知，因此还需要针对此问题设计一个子算法，使得排牙算法设计完整。本文将碰撞检测和调整融为一个环节，即在对相邻牙齿间进行碰撞检测之后，根据相邻牙齿间距做出相应的迭代调整。牙齿间碰撞检测借鉴了基于矩形包围盒的方法[21]，图10中被选牙齿与近中相邻牙齿相距<0.1 mm、与远中相邻牙齿相距约0.2 mm，在临床口腔正畸治疗中，牙齿间距≤0.5 mm最为理想[14]。

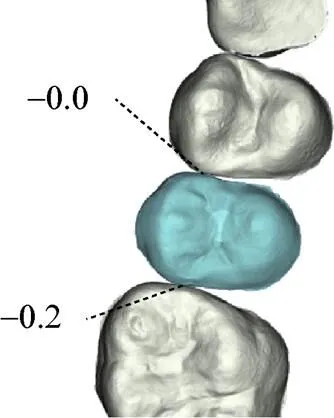
图10 碰撞检测牙齿间距(mm)

在碰撞检测基础上，本文针对拟合优化后出现的牙齿碰撞问题设计了迭代调整算法，其思想是：以第一磨牙为基准，上下颌左右两侧牙齿均从远中往近中方向逐颗进行调整，根据碰撞检测计算出待调整牙齿与相邻其牙齿之间的间距后，由间距大小判断往近中方向还是远中方向平移，并采用最速下降法迭代调整，其中对第二磨牙和第三磨牙，则是从近中往远中方向进行调整。在迭代调整牙齿位置的同时也需要结合图9调整牙齿的姿态。对单颗牙齿作调整的算法步骤如下：

步骤1. 计算待调整牙齿与相邻牙齿的间距，若远中方向相邻牙齿间距>0.5 mm或<0，则跳转到步骤2，否则跳出迭代；

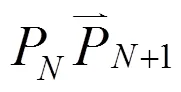
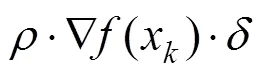
步骤4. 将待调整牙齿按位移量平移，并对应图9中的拟合函数，根据轴位移量作牙齿唇(颊)舌侧、近远中方向及自旋转姿态调整，调整结束后跳转至步骤1。

按照上述迭代调整算法还存在边界问题，从第一磨牙往近中方向逐个牙齿调整，可能出现如图11所示的2种情况，其原因是由于拟合的空间曲线不足以让牙齿整齐排列或者是排列位置有多余。针对该问题，本文采用的解决方案为通过调整式(2)模型的参数，寻找一条曲线的弧长为作为牙弓周长，即

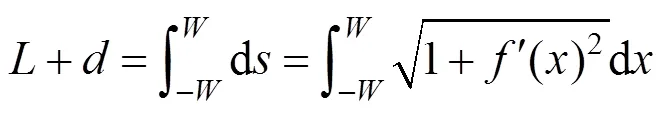
其中，L为式(2)模型f(x)在区间[–W, W]的弧长；W为牙弓宽度，指单颌左右两侧第一磨牙远中颊侧尖点的距离，经过前面算法对牙列的调整，牙齿能够沿牙弓线紧密排列，因此计算的曲线弧长近似为牙弓周长。由左右中切牙间距d判断，通过改变式(2)模型的参数实现对图12中曲线的缩进或扩展，其中，图11(a)的中切牙间距d<0，f(x)需作扩展微调，图11(b)的中切牙间距d>0.5 mm，f(x)需作缩进微调，微调过程中同时保持牙齿间距，通过微调获取合适的拟合曲线后，重新执行迭代调整算法使得牙列排列整齐。

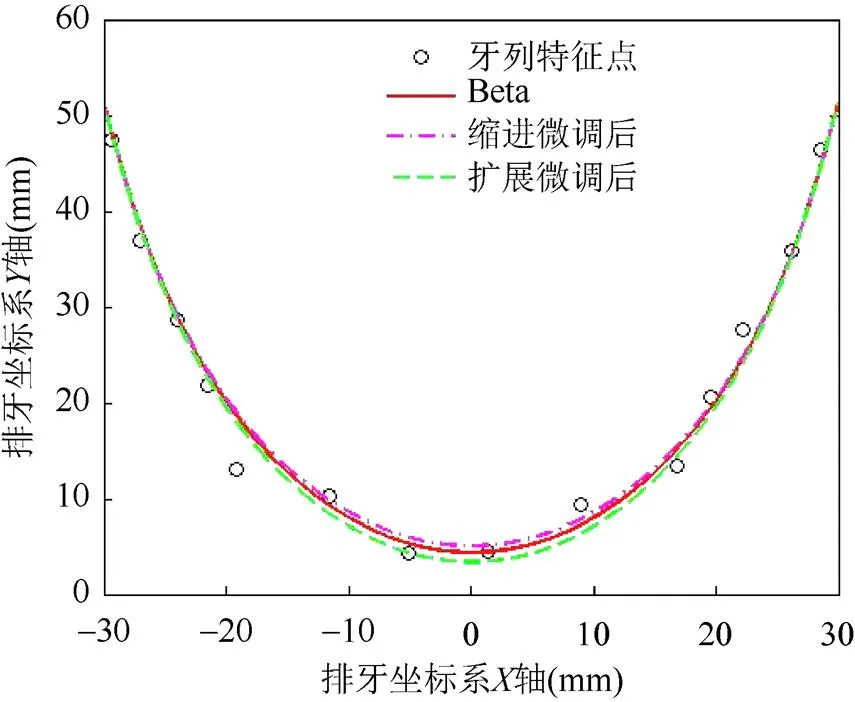
图12 边界问题处理

2.3 排牙算法

输出：排列完成的牙齿模型。

算法步骤：

步骤1. 输入牙齿模型，建立排牙坐标系；

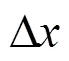
步骤5. 执行碰撞检测及迭代调整算法：

步骤5.1. 上下颌左右两侧牙齿均以第一磨牙为基准，对于第二前磨牙至中切牙，从远中方向往近中方向对牙齿逐颗进行调整；

步骤5.2. 同样以第一磨牙为基准，对于第二、第三磨牙，从近中方向往远中方向对牙齿逐颗进行调整；

步骤5.3. 判断是否存在边界问题，若存在，则作相应处理，处理完成后跳至步骤5；否则，结束迭代调整；

步骤6. 输出排列完成的牙齿数据。

3 实 验

实验使用Intel i5-3470 3.20 GHz CPU计算机、Visual Studio 2016开发平台、VTK工具包，在具有自主知识产权的排牙软件e-Set(1.4v)的环境下实现前文介绍的自动排牙算法，采用的10组牙齿数据均由广州瑞通生物科技有限公司提供。所有数据从开始执行算法到排好牙列，平均花费时间约48 s，相比于专家人工排列牙齿所花费的时间有很大改善。

3.1 排牙前后对比

以图1样例数据为输入，执行本文算法，结果如图13(a)和图13(b)所示，说明本文算法能够同时将各颗牙齿在局部范围内经平移或旋转调整至合适的姿态。对照图13(c)与表1，以上颌为例，可以直观看出各颗牙齿的平移量和旋转量，其中旋转量以正对坐标轴方向，逆时针旋转为正，顺时针旋转为负。例如，样例数据中的上颌左侧中切牙(牙号11)在正畸治疗时需要绕轴顺时针旋转32.005°，上颌右侧侧切牙(牙号22)在正畸治疗时在轴正方向的平移量为2.193 mm、在轴负方向的平移量为2.853 mm。就样例数据而言，主要的移动量集中在两侧前牙、右侧前磨牙、两侧第二磨牙，两侧第一磨牙移动量相对较少。理论上，样例数据第二磨牙的初始位置相对咬合面偏高，需要压低位置，应用本文算法也得到较好的调整，但在实际正畸治疗中对第二磨牙矫正的难度较大。

图14为部分不同程度畸形的牙颌数据的排牙前后对比，其畸形程度依次递增。可以看出，本文算法应对不同程度的畸形牙颌，仍可取得不错的效果。在实验中，除了定义牙齿特征点和调整权值参数，其余过程均为自动。

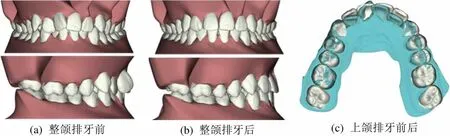
(a) 整颌排牙前(b) 整颌排牙后(c) 上颌排牙前后

(a) 整颌排牙前(b) 整颌排牙后

表1 上颌牙齿排牙后的移动量和旋转量

偏移量牙号 1112131415161721222324252627 △x(mm)–0.638–2.392–0.447–1.207–0.7010.3260.1111.3952.1930.9841.4241.2390.008–0.638 △y(mm)–1.699–3.0750.798–0.340–0.399–0.0090.024–3.002–2.853–0.394–0.287–0.2540.098–1.699 △z(mm)0.1290.652–1.339–0.0840.1320.637–0.3950.552–0.158–1.079–0.0120.2600.4270.129 △φ(°)–1.0460.7021.8522.486<0.001–2.5870.323–3.3661.8451.4980.4643.4872.284–1.046 △θ(°)14.432–5.9933.5756.0002.515–3.548–6.801–2.997–2.0130.109–6.511–3.0823.00614.432 △ψ(°)–32.00521.440–6.011–2.950–4.4935.5393.4952.9992.590–7.0026.458–0.499–4.494–32.005

3.2 与人工排牙结果对比

衡量算法自动排牙结果质量的好坏可以通过对比人工排牙的结果来检验，且CAD能提供精确的测量手段。引用文献[22]提到的牙颌测量比较方法，测量项如图15所示，以样例数据为实验数据分别按照颌宽、整颌、上下颌覆盖测量为标准进行自动排牙与人工排牙结果对比，测量结果对比如图16所示。

从图16中可以看出，本文自动排牙算法的排牙结果与人工排牙结果相比差距较小，证明本文算法可以替代人工排牙。其中，人工排牙上颌颌宽测量项结果比自动排牙结果略宽，差距均在1 mm之内，下颌颌宽测量项则平均相差不大。

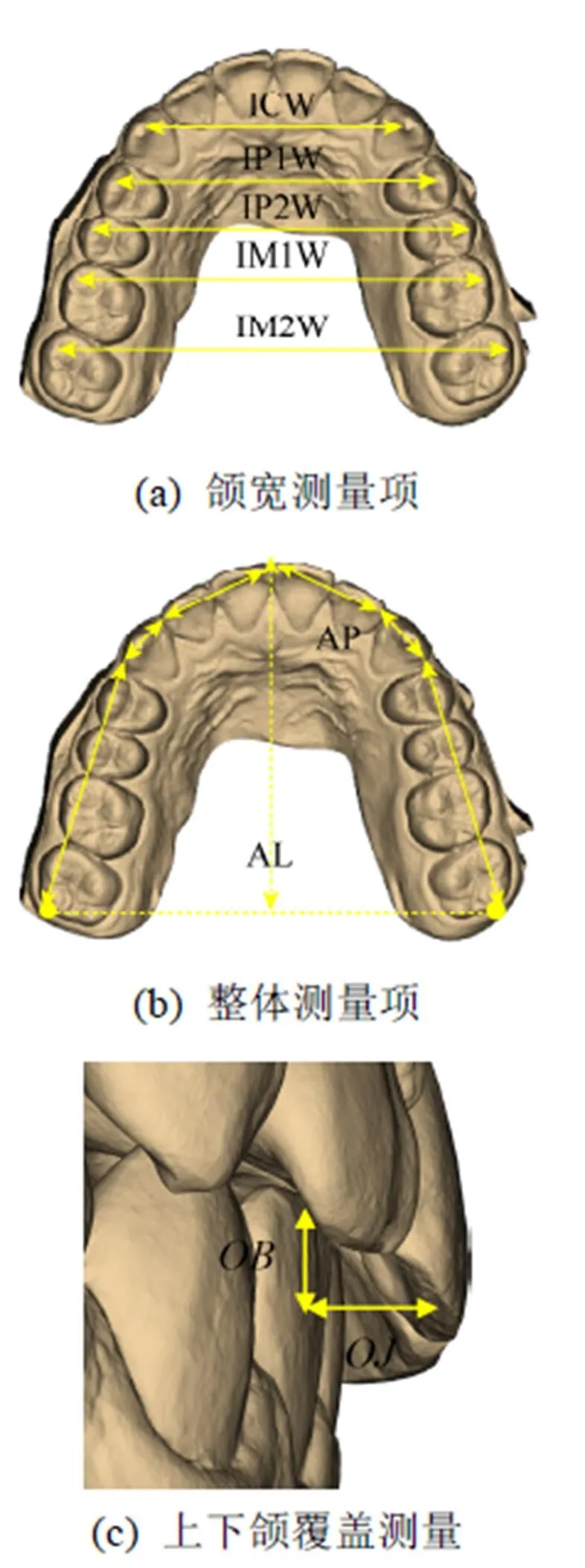
图15 单颌测量项

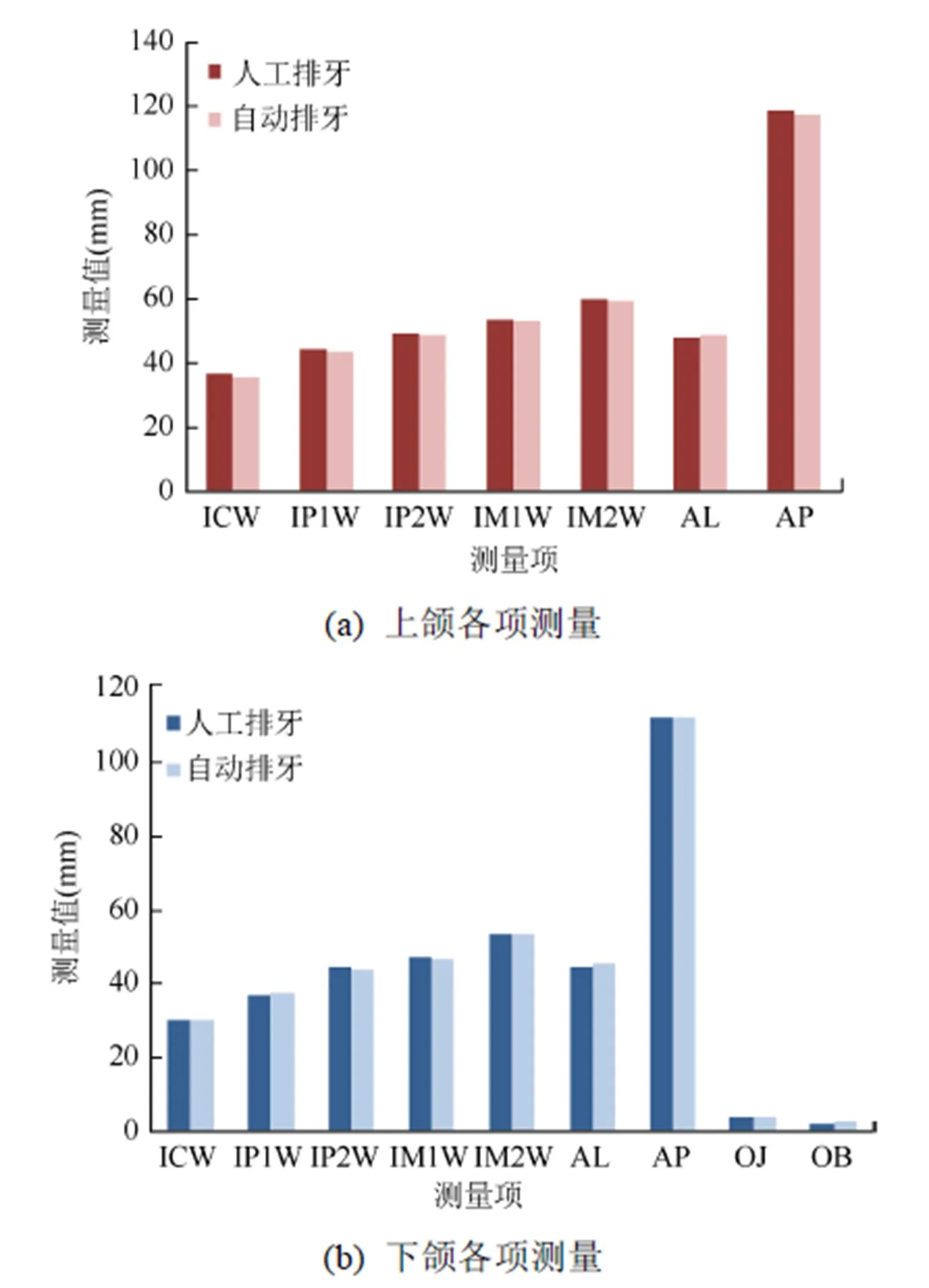
图16 人工排牙与自动排牙测量对比

3.3 与现有排牙方法对比

与文献[7]相比，其采用美国正畸学会客观评分系统(ABO-OGS)作为评分标准，该评分标准均为整数型数据，导致算法迭代次数过高(约400次)，而本文算法平均执行时间在48 s左右，在进行迭代调整之前已经将牙齿位姿约束到空间曲线上，采用最速下降法即可满足迭代需求，迭代次数远低于文献[7]方法。文献[11]与文献[13]研究思路均为义齿排牙，将2篇文献中所述算法与本文算法进行比较，对比结果如图17所示，义齿排牙算法是以咬合面上的二维牙弓线为依据，排列后的牙列Spee曲线平整，而采用本文算法排列后的牙列Spee曲线具有一定深度，是由于考虑了牙齿在空间中的位姿，因此本文算法更贴近实际正畸治疗。

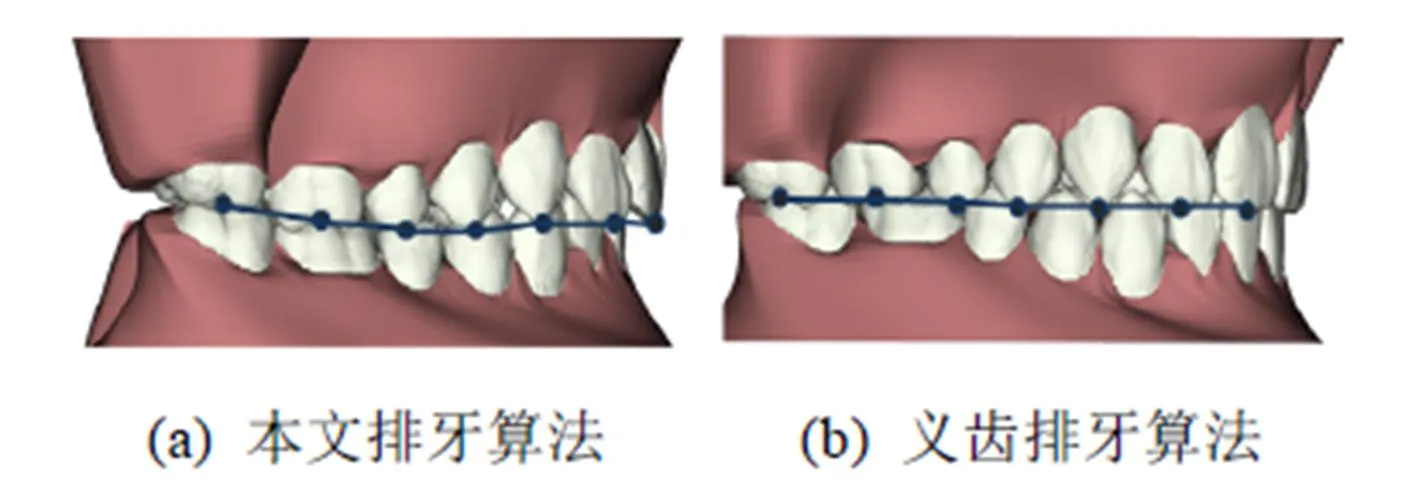
图17 排牙算法对比图

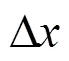
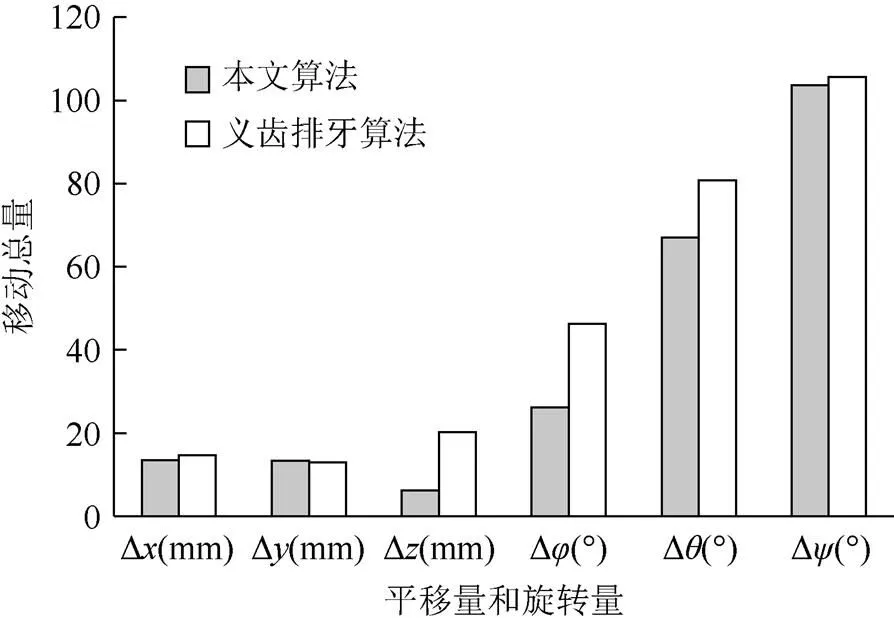
图18 平移和旋转移动总量对比

4 结束语

本文针对人工排牙效率低下问题，结合CAD在口腔正畸领域中的应用，设计一种基于拟合优化的错位牙齿自动排列方法，并应用该方法对多组数据进行实验，其结果表明，本文算法能够将错颌牙列各颗牙齿平移旋转至目标位置，得到的牙列与人工排牙结果对比相差无异，能够大幅减少人力；与现有排牙算法对比，计算效率高，更贴近临床牙齿矫治，且在牙齿移动代价方面优势明显。在今后工作中，将进一步研究牙齿正畸路径规划。

[1] 范然, 钮叶新, 金小刚, 等. 计算机辅助牙齿隐形正畸系统[J]. 计算机辅助设计与图形学学报, 2013, 25(1): 81-92.

[2] 高洪涛, 颜永年, 祁鹏, 等. 三维数字牙颌模型分析诊断系统设计[J]. 计算机辅助设计与图形学学报, 2005, 17(6): 1322-1328.

[3] REKOW E D, ARTHUR G E, DONALD R R, et al. CAD/CAM for dental restorations-some of the curious challenges [J]. IEEE Transactions on Biomedical Engineering, 1991, 38(4): 314-318.

[4] MOTOHASHI N, KURODA T. A 3D computer aided design system applied to diagnosis and treatment planning in orthodontics and orthognathic surgery [J]. European Journal of Orthodontics, 1999, 21(3): 263-274.

[5] ALAN C L, KUOJONG C, WU PAITING, et al. 3D CAD for design of invisible tooth aligner [C]// Proceedings of the 2005 IEEE International Conference on Mechatronics. New York: IEEE Press, 2005: 647-651.

[6] 王先泽, 李忠科, 马亚奇, 等. 一种基于PSO的自动化排牙方法[J]. 计算机工程与应用, 2012, 48(5): 211-212.

[7] KUMAR Y, JANARDAN R, LARSON B. Automatic virtual alignment of dental arches in orthodontics [J]. Computer-Aided Design and Applications, 2013, 10(3): 371-398.

[8] CHO M Y, CHOI J H, LEE S P, et al. Three dimensional analysis of the tooth movement and arch dimension changes in class I malocclusions treated with first premolar extractions: A guideline for virtual treatment planning [J]. American Journal of Orthodontics and Dentofacial Orthopedics, 2010, 138(6): 747-757.

[9] ZHANG Y D, ZHAO Z F, LU P J, et al. Robotic system approach for complete denture manufacturing [J]. IEEE/ASME Transactions on Mechatronics, 2002, 7(3): 392-396.

[10] ZHANG Y D, JIANG J G, LV P J, et al. Coordinated control and experimentation of the dental arch generator of the tooth-arrangement robot [J]. International Journal of Medical Robotics and Computer Assisted Surgery, 2010, 6(4): 473-482.

[11] ZHANG Y D, JIANG J G, LIANG T, et al. Kinematics modeling and experimentation of the multi-manipulator tooth-arrangement robot for full denture manufacturing [J]. Journal of Medical Systems, 2011, 35(6): 1421-1429.

[12] SUN Y C, LV P J, WANG Y. Study on CAD&RP for removable complete denture [J]. Computer Methods and Programs in Biomedicine, 2009, 93(3): 266-272.

[13] CHENG C, CHENG X S, DAI N, et al. Personalized orthodontic accurate tooth arrangement system with complete teeth model [J]. Journal of Medical Systems, 2015, 39(9): 1-12.

[14] CASKO J S, JAMES L V, VINCENT G K, et al. Objective grading system for dental casts and panoramic [J]. American Journal of Orthodontics and Dentofacial Orthopedics, 1998, 114(5): 589-599.

[15] 石飞, 冯翠娟, 赵阳, 等. SNA、SNB、ANB角与常用头影测量项目的相关性分析[J]. 口腔医学, 2010, 30(10): 596-599.

[16] 袁天然, 廖文和, 程筱胜, 等. 三维牙颌模型的牙齿形状建模方法[J]. 计算机辅助设计与图形学学报, 2010, 22(4): 703-710.

[17] 曹沅, CHING C K, DELONG R. 关于牙科学中的一类最优化问题的解[J]. 计算机辅助设计与图形学学报, 2005, 17(8): 1778-1784.

[18] 于跃, 许天民. Spee曲线相关研究的回顾[J]. 中华口腔正畸学杂志, 2013, 20(4): 214-217.

[19] 姜金刚, 张永德. 牙弓曲线发生器的运动规划与仿真[J]. 哈尔滨理工大学学报, 2013, 18(1): 32-36.

[20] 毛晓燕, 陈丹鹏. 牙转矩及其临床意义[J]. 上海口腔医学, 2009, 18(6): 656-660.

[21] 周之平, 张飒兵, 吴介一, 等. 基于矩形包围盒的多边形碰撞检测算法[J]. 中国图象图形学报, 2004, 9(11): 1294-1303.

[22] JOON L, JUNG Y C, KEE J L, et al. Comparison of virtual and manual tooth setups with digital and plaster models in extraction cases [J]. American Journal of Orthodontics and Dentofacial Orthopedics, 2014, 145(4): 434-442.

Automatic Alignment Method for Malocclusion in Virtual Orthodontics Treatment

LI Zhan-li1, FU Jing-ding1, LI Hong-an1, ZHOU Kang1, HUI Qiao-juan2

(1. College of Computer Science and Technology, Xi’an University of Science and Technology, Xi’an Shaanxi 710054, China; 2. Department of Mechatronics Power and Information Engineering, China University of Mining and Technology Yinchuan College, Yinchuan Ningxia 750021, China)

Aiming at the problem of low efficiency of teeth arrangement by artificial teeth in virtual orthodontics treatment technology, this paper proposes an automatic alignment method for malocclusion based on fitting optimization. Firstly, we create a coordinate system for the input dental model, define single tooth feature points and establish the local coordinate system of teeth. On this basis, the position and posture of each tooth in the dentition is analyzed from a lower dimension. The weighted fitting optimization method is employed to calculate the coordinate translation and local axis rotation of tooth which forms the association constraints of the position, posture of teeth and the spatial dental curves. Then, combined with the collision detection method of rectangular bounding box, we design an iterative algorithm based on method of steepest descent to adjust the position and posture of teeth within the constraints of spatial dental curves. The experimental results show that the teeth alignment is similar to artificial alignment of teeth, and the alignment efficiency is highly improved. The proposed method is not only more like clinical orthodontics, but also reduces the total cost of teeth movement compared with the existing teeth alignment method.

virtual orthodontics; automatic teeth alignment; weighted fitting; optimization

TP 391

10.11996/JG.j.2095-302X.2019020225

A

2095-302X(2019)02-0225-10

2018-09-03；

2018-09-14

宁夏高等学校科学研究项目(NGY2017234)；陕西高等教育教学改革研究项目(17BY040)；西安科技大学博士启动金项目(2019QDJ007)；陕西省自然科学基础研究计划项目(2019JM-162)

李占利(1964-)，男，陕西周至人，教授，博士，博士生导师。主要研究方向为计算机图形学、图像处理等。E-mail：lizl@xust.edu.cn

李洪安(1978-)，男，山东武城人，副教授，博士，硕士生导师。主要研究方向为图形图像处理、机器视觉等。E-mail：an6860@126.com