钢纤维-混凝土基体界面粘结性能数值分析

王 力

(武汉大学 土木建筑工程学院， 湖北 武汉 430072)

传统的普通混凝土材料有着抗拉强度低、延性差等弱点，难以满足复杂的结构形式的需求。在混凝土中掺入钢纤维后，可以有效控制宏观裂缝，同时可大幅度提升材料基本力学性能[1-4]，因此，钢纤维混凝土作为一种高性能混凝土正逐步应用于工程中。钢纤维混凝土在发生开裂时，裂缝处纤维被拔出，此时钢纤维的增强潜力并未充分发挥，研究纤维与混凝土基体间的粘结性能及其影响因素，进而进行合理的优化设计，提高钢纤维混凝土力学性能、充分发挥纤维增强效果。

近年来，各国学者对钢纤维与混凝土基体界面间的粘结性能从多个角度展开了研究。赵丽军等[5]和陈沛然等[6]通过单根纤维拉伸试验研究基体强度对粘结性能的影响，结果表明：随着基体强度的增大，最大拉拔力和耗散能有所增强。代超[7]利用丁苯乳液和硅灰来对混凝土进行改性处理，研究了添加剂对钢纤维与混凝土基体间的界面粘结性能的增强效果。王家赫等[8]推导了圆直纤维与混凝土基体界面间粘结强度的理论模型并利用试验验证，预测了峰值拔出荷载与纤维埋置夹角的数值关系。Edmunds Zīle等[9]提出了纤维形状对纤维从水泥基体中拔出峰值荷载的理论模型模型。赵燕茹等[10]采用数字图像与试验相结合的方法，测量钢纤维从混凝土基体拔出过程中界面的应变分布及变化规律，并实时观测界面变化，结果表明，微细观尺度上的应变局部化导致了纤维界面剪切破坏的局部化现象，并不断产生、发展和转移。

然而，多数工程上涉及的材料种类及形状多样，无法通过传统的数学和力学方法解决实际问题，随着计算机技术的飞速发展，数值模拟逐渐成为了土木工程领域解决问题不可或缺的手段。现有的混凝土数值分析研究中，大多采用有限元软件，将混凝土等效成一种均匀而连续的材料。实际上，混凝土是一种非均质材料，有限元单元法模型无法在细观尺度上体现骨料的形状以及在基体中的随机分布情况，同时，也不能反映骨料与钢纤维间复杂相互作用，研究手段存在不足。在离散元建模的研究中，Ferelle等[11]通过控制形状精度参数，得出了在合理数量的基本单元的情况下，生成形状和锐度精度较高的复杂单元的方法，该方法可以用于生成混凝土模型。宿辉等[12]也利用PFC模拟生态混凝土的双轴试验，得到了不同细观参数对混凝土应力和微裂纹的影响关系。

鉴于此，应用离散元方法，通过PFC软件模拟钢纤维在混凝土基体中的单根纤维拔出试验，不仅可以精确地模拟纤维和骨料的形状以及在混凝土基体中的随机分布情况，还能有效分析宏观和细观参数对钢纤维与混凝土界面间粘结性能的影响，对以后建立数值模型和参数标定提高参考，具有十分重要的意义。

1 颗粒流数值模拟基础理论

在PFC数值建模中，以如下假设为基础[13]：

(1) 所有的颗粒单元不会发生变形和破坏，均被视为刚体。

(2) 颗粒间的接触处允许有相对颗粒半径较小的重叠量。

(3) 接触力和颗粒间的重叠量由力-位移定律建立联系。

相比连续介质模型不同的是，组成PFC模型的基本单元是颗粒单元和墙单元。颗粒单元为圆盘或球体，是组成材料介质的基本单元，可以通过块或簇的构成方式，将多个颗粒组合形成任意形状的组合体。墙单元是生成模型边界条件的单元，不能直接被施加力的边界条件，只能通过施加速度从而间接达到颗粒的位移和力的边界条件。

PFC模型中，单元间存在孔隙且可不连续，故颗粒间的运动不需要满足变形协调方程，仅需满足内置的物理方程和平衡方程。整个分析过程中，颗粒单元的运动状态(位置和力)都在时刻发生改变，一方面颗粒单元的接触力通过力-位移关系更新，另一方面颗粒单元的位置依据牛顿第二定律更新，以重新调整颗粒间的接触关系，二者交互作用，直至达到平衡状态或者发生破坏无法保持稳定状态，如图1[13]所示。

图1PFC迭代过程示意图[13]

在PFC模型中，由接触模型来反映颗粒之间接触力与相对位移之间的关系，主要分为接触刚度模型、接触滑动模型和粘结模型。其中，粘结模型分为接触粘结模型和平行粘结模型，接触粘结模型仅靠接触点处沿法向和切向的弹簧实现，只能传递力；平行粘结模型通过颗粒间一定截面形状和尺寸的粘结材料将颗粒粘结，该粘结可视作一组有恒定法向刚度和切向刚度的弹簧均匀分布于接触处，可以传递力和弯矩，如图2所示。

图2平行粘结模型示意图

对于混凝土的PFC接触模型，一般采用平行粘结模型，颗粒之间被赋予粘结力，当其中任意一个方向的最大应力超过相应的粘结强度时，平行粘结就会发生破坏，相互接触的颗粒发生相对滑动，受摩擦力作用。

2 混凝土中钢纤维拔出模型的建立

国内外对钢纤维与混凝土基体间粘结性能的研究方式主要是单根纤维拉拔试验，数值模拟可对试验研究进行重要补充，本文利用PFC3D软件建立混凝土中钢纤维拔出模型，分析了各参数对钢纤维-混凝土基体界面间粘结性能产生的影响，为进一步揭示纤维拔出过程中纤维、混凝土基体以及纤维-基体界面的破坏和失效全过程奠定基础。

由于圆直形钢纤维形状简单，在拉拔的过程中，可忽略其锚固作用，只通过化学粘结力和摩擦力与附近区域的混凝土基体发生相互作用。张红州[14]研究了纤维在不同厚度基体中拔出的极限载荷，并描绘了基体的应力场等值线分布图，结果表明，纤维的脱粘与拔出，对基体剪应力大小的影响是有限的，随着离开纤维距离的增大，基体应力逐渐减小，因此，在计算纤维从混凝土基体的拉拔过程时，基体尺寸不必取的太大。龙雪[15]在研究纤维-基体界面粘结机理时所取基体的尺寸为15 mm×10 mm。考虑纤维和石子的直径、软件计算效率以及基体影响范围，计算模型中的混凝土基体选取钢纤维附近20 mm范围，并以Deng等[16]所进行的单根圆直纤维拉拔试验为参考进行建模，步骤如下：

(1) 围绕40 mm×40 mm×50 mm的区域生成墙单元。

(2) 生成钢纤维长度为30 mm，直径为0.72 mm的钢纤维。

(3) C40混凝土配合比，生成相应数量的粗骨料单元和水泥砂浆单元以构成混凝土基体。

(4) 赋予颗粒单元间接触计算模型。

(5) 赋予钢纤维恒定速度，进行位移控制加载，同时获取钢纤维所受粘结力-滑移曲线。

PFC混凝土模型中，粗骨料单元由531个基本颗粒单元组合生成，并视为一个整体，粗骨料内部颗粒无相对运动，其三视图如图3所示。各介质单元的位置和方向均服从随机分布，单元信息见表1，其中，颗粒单元密度为我国石子和砂的平均表观密度。生成的钢纤维拉拔模型和钢纤维埋置处的剖面图分别如图4和图5所示。

图3 粗骨料模型

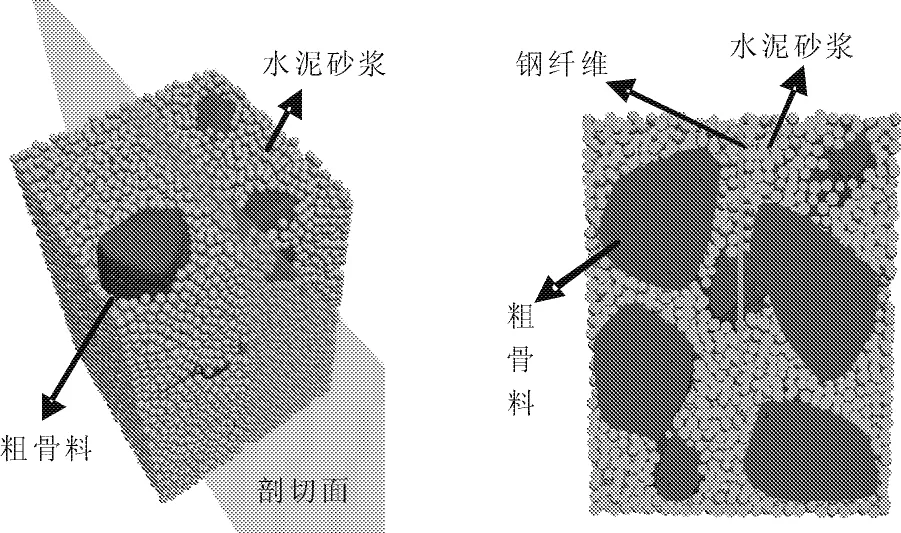
图4钢纤维拉拔模型 图5模型剖面图

对于混凝土材料的接触计算模型，选用线性平行粘结模型。为防止颗粒单元的接触关系在钢纤维拉拔的过程中随颗粒位置变化而二次生成，采用Contact method命令进行接触模型的参数赋值。为研究相关模型参数对钢纤维-基体粘结性能的影响，设置了相关对照组以进行计算和分析，见表2。

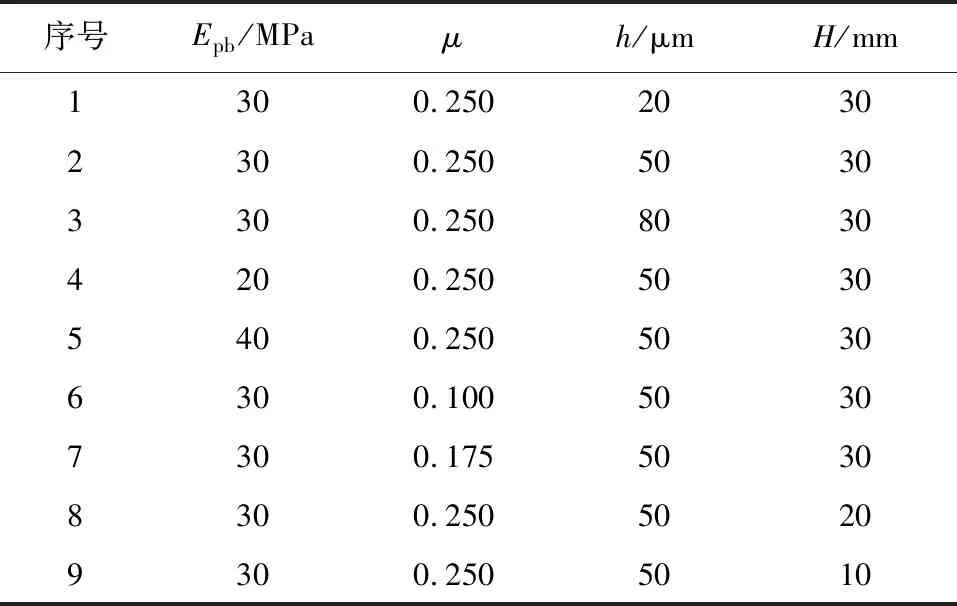
表2 模型参数

注：Epb为平行粘结变形模量、μ为摩擦系数、h为粘结层厚度、H为纤维埋置深度。

3 离散元参数影响分析

3.1 粘结层厚度影响分析

粘结层厚度反映了允许颗粒单元之间产生粘结作用的最大距离，粘结层厚度分别为20 μm、50 μm及80 μm时钢纤维与混凝土基体间粘结力与滑移的关系曲线如图6所示。

粘结层厚度不同时，纤维与基体的粘结力峰值差异较大，但粘结力峰值所对应的滑移均为0.11 mm左右。粘结层厚度为20 μm时，粘结力峰值为46.7 N；粘结层厚度为50 μm时，粘结力峰值为59.6 N；粘结层厚度为80 μm时，粘结力峰值为77.2 N。对比不同粘结层厚度下的钢纤维与基体间的粘结力峰值可见，增加颗粒单元间粘结层厚度，粘结力峰值将提升，而峰值滑移基本无变化。该现象表明，粘结层厚度增加后，钢纤维能与附近更多的基体颗粒产生粘结作用，与混凝土基体脱粘前，钢纤维的拉拔会受到更大的抵抗，从而使得钢纤维与混凝土基体间的粘结效应更好，说明钢纤维混凝土即将发生开裂时，粘结层厚度越大，对抵抗混凝土开裂效果越好。

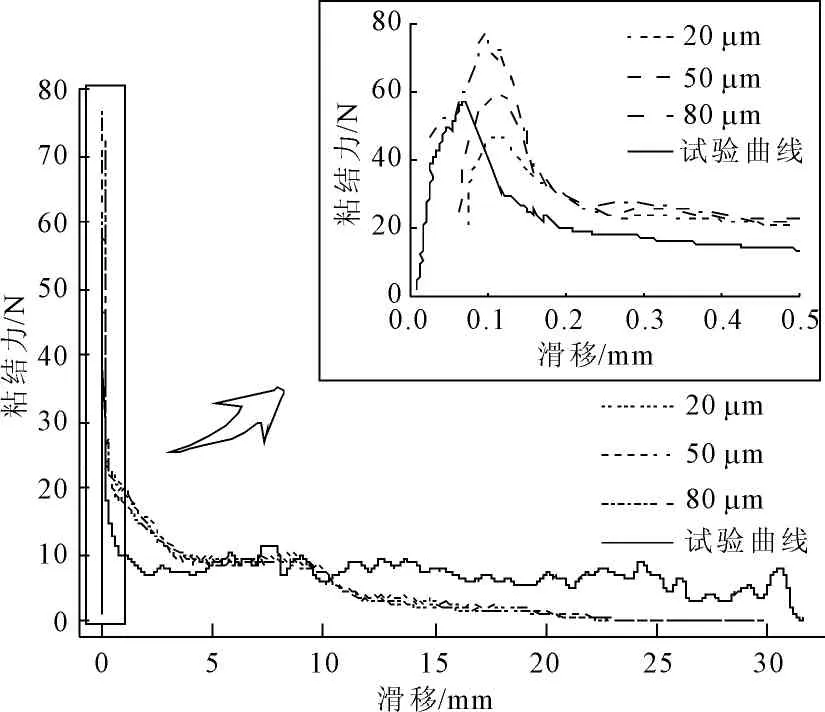
图6粘结层厚度对纤维-基体粘结性能影响

3.2 平行粘结变形模量影响分析

当颗粒间处于粘结状态时，平行粘结可以抵抗弯矩和力，一旦粘结处产生的应力达到平行粘结破坏强度时，平行粘结就会发生破坏，接触模型将退化为线弹性模型。

平行粘结变形模量分别为20 MPa、30 MPa和40 MPa时钢纤维与混凝土基体间粘结力与滑移的关系曲线如图7所示。

图7平行粘结变形模量对纤维-基体粘结性能影响

平行粘结变形模量不同时，纤维与基体的粘结力在滑移为0～0.3 mm时差异较大，粘结力峰值以及对应的滑移也有所差异。平行粘结变形模量为20 MPa时，粘结力峰值为60.4 N，对应滑移为0.145 mm平行粘结变形模量为30 MPa时，粘结力峰值为59.6 N，对应滑移为0.119 mm；平行粘结变形模量为40 MPa时，粘结力峰值为57.0 N，对应滑移为0.101 mm。对比可发现，增大接触模型中的平行粘结变形模量，粘结力峰值减少，粘结力峰值也将提前到达，钢纤维混凝土的脆性增加。

3.3 摩擦系数影响分析

在宿辉[10]的混凝土PFC模型中，摩擦系数取值范围为0.01～0.50，摩擦系数在0.01～0.10范围内变化时对模型计算较小，故在本模型中取摩擦系数分别为0.100、0.175和0.250进行研究，钢纤维与混凝土基体间粘结力与滑移的关系曲线如图8所示。

图8摩擦系数对纤维-基体粘结性能影响

滑移处于0～3 mm范围内时，不同摩擦系数下的粘结力-滑移曲线差异较大，摩擦系数为0.100时，粘结力峰值为39.5 N；摩擦系数为0.175时，粘结力峰值为46.9 N；摩擦系数为0.250时，粘结力峰值为59.6 N。粘结力-滑移曲线达到峰值后，粘结力随着钢纤维的拔出而迅速下降，滑移为0.5 mm～3.0 mm范围内时，在摩擦系数越大的模型中，钢纤维受到的粘结力越大，说明摩擦系数对粘结力峰值以及纤维与基体脱粘后的粘结力呈正相关，摩擦系数越大对混凝土防开裂效果越好。

3.4 纤维埋置深度影响分析

埋置深度分别为10 mm、20 mm及30 mm时钢纤维与混凝土基体间粘结力与滑移的关系曲线如图9所示。

对图9中曲线进行积分可得钢纤维拔出时消耗的拉拔功，粘结力峰值除以钢纤维表面积可得粘结强度，如表3所示。

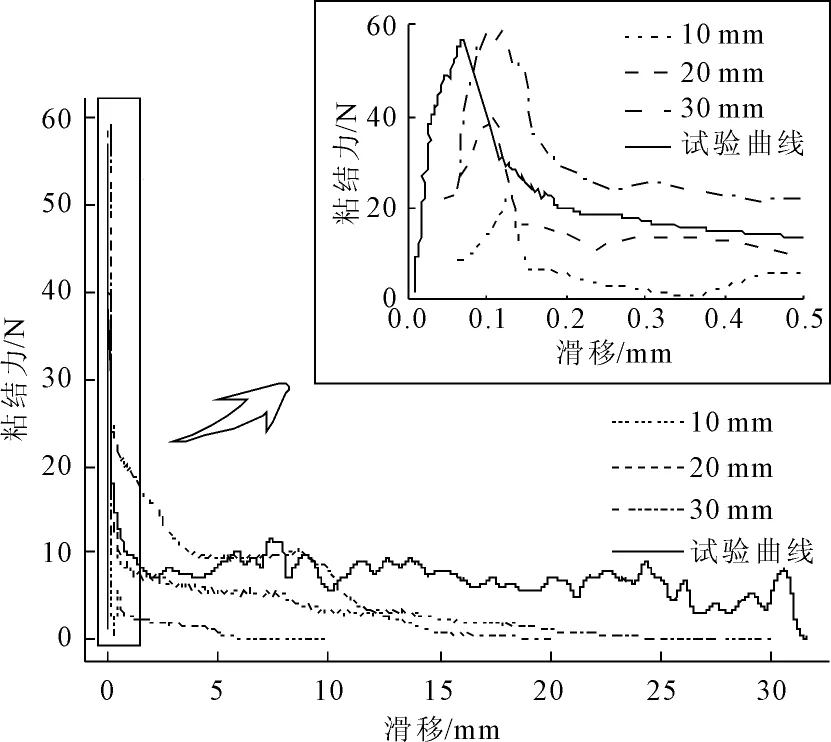
图9 纤维埋深对纤维-基体粘结性能影响

数据表明，随着钢纤维埋置长度的增大，钢纤维与基体间的粘结力和拉拔功将大幅度增加，拉拔功的增长幅度远远大于纤维埋置长度的增加倍数，但粘结强度稍有降低，总体上粘结性能得到了较大提升，说明钢纤维长度为10 mm～30 mm范围时，长度越长，对抵抗混凝土开裂效果越好。

4 结 论

本文基于单根钢纤维拔出的PFC3D离散元数值模拟，记录了钢纤维在拔出过程中与混凝土基体间的粘结力，并分析了PFC3D模型中钢纤维与混凝土基体间的粘结力随粘结层厚度、平行粘结变形模量、摩擦系数、纤维埋置深度的变化规律。主要结论如下：

(1) 粘结层厚度的增加，使钢纤维能与附近更多的基体颗粒产生粘结作用，从而使得钢纤维与混凝土基体间的粘结效应更好，对抵抗混凝土开裂有利。

(2) 平行粘结弹性模量的增大，会导致粘结力峰值减少，粘结力峰值的出现呈现提前性，钢纤维混凝土的脆性增加。

(3) 摩擦系数主要影响粘结力-滑移曲线的形状和粘结力峰值，随着摩擦系数增大，颗粒之间的相互运动受到抑制，颗粒之间的摩擦力增大，粘结力增加，对抵抗混凝土开裂有利。

(4) 纤维埋置深度在10 mm～30 mm内增加，可以大幅度提升纤维与混凝土间的粘结力及拉拔功，但粘结强度稍有减低，对抵抗混凝土开裂有利。