重力对土体中地下结构地震反应的影响
2019-05-13董正方师成力王君杰曾繁凯
董正方, 师成力, 王君杰, 曾繁凯
(1. 河南大学 岩土与轨道交通工程研究所, 河南 开封 475004; 2. 同济大学 土木工程防灾国家重点实验室, 上海 200092)
0 引言
分析地下结构的地震反应时,工程设计中的常用做法是作用组合,即将结构所受的重力作用和地震作用分开考虑,得到各自的结果后再进行叠加。从理论上来说,这种作用组合方法对于线性情况适用而非线性情况并不适用。但为了分析简便,目前,对非线性情况也常采用线性叠加方式。这种方式对于地上结构误差较小,但对于埋入土体中的地下结构,由于土体中存在初始地应力,且土体在地震作用下很容易进入非线性状态,因此,可能会存在较大的误差。
目前,国内外学者对地下结构地震反应涉及的一些问题进行了研究。高峰等[1]通过同时考虑静力效应和动力效应的地下结构静-动力分析方法,推荐了一种较为合理的地下结构静-动力分析的人工边界转换方法; 赵密等[2]基于改进的动力刚度连分式逼近方法,为频域解析解的精确人工边界条件转换为时域高精度人工边界条件提供了方法; 文献[3-4]研究了土体的非线性处理方式; 文献[5-6]探讨了地下结构地震反应的简化分析方法; 汪精河等[7]对比3种地震输入方法并进行算例分析得出黏边弹性边界,采用应力输入的方法进行地震输入; 刘晶波等[8]基于波动法和有限元法的特点,提出直接求解等效地震荷载然后进行地震输入的方法; 刘立平[9]和董正方等[10]等讨论了重力的分析方法,但对该方法以及重力对地下结构地震反应的影响程度等研究还不充分。因此,本文将从重力对土体特性的影响、重力对地下结构地震反应影响的分析方法、重力对地震反应影响的程度等几个方面开展研究。
1 重力对地震反应的影响
1.1 重力对土体性质的影响
土体初始应力主要受重力影响,深度越大则自重应力越大。另外,同样的土体在不同的埋深处,由于其自重应力不同造成的力学特性也不同。在自重作用下,土体表现为压硬性和剪胀性。当土体的本构关系采用黏弹性或等效线性时,需要知道最大剪切模量Gmax(或初始剪切模量G0)、阻尼比λ、剪切模量比和阻尼比随剪应变的试验曲线等。其中,对于Gmax和λ,围岩压力对其有显著影响,例如文献[11]通过分析上海深厚场地的地震反应得出,在大震作用时,宜考虑围岩压力对土体特性的影响,而剪切模量比、阻尼比随剪应变的经验曲线受土体性质等诸多因素影响[12]。因此,重力因素主要是通过围岩压力影响土体性质,最大剪切模量受围岩压力影响较大,围岩压力越大,剪切模量越大。剪切模量比曲线随围岩压力增加不变或增加不大,其中,砂土受到的影响较小,黏土受到的影响较大。阻尼比曲线随围岩压力增加不变或减小。
1.2 重力与地震相互影响
地下结构的地震反应主要受周围土体变形影响,土体受到的重力荷载和地震荷载也会影响土体的变形。因此,重力和地震对地下结构的影响是不能分开来考虑的。重力产生正应力σ和正应变ε(见图1(a)),垂直输入剪切波产生剪应力τ和剪应变γ(见图1(b))。对于二维和三维问题,为方便研究,经常采用一些特殊的应力,如八面体应力和应变。

图1 应力-应变图Fig. 1 Diagram of stress and strain
八面体正应变为
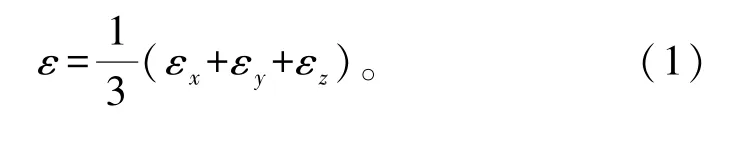
八面体剪应变为

式中:ε为正应变,下标x、y、z代表3个方向的主应变;γ为剪应变。
在重力与地震相互作用中,当土体进入非线性时,在地震作用下会引起刚度变化,进而引起正应变和剪应变变化;土体正应变和剪应变的变化反过来也将引起土体刚度变化。因此,重力与地震是相互影响的。
2 重力作用下的地震反应计算方法
2.1 初始应力的处理
土体在自重作用下已经完成的固结变形称为先期固结变形。然而,固结完成前,土体尺寸是未知的,因此,有限元计算模型尺寸需根据固结完成后的尺寸确定。如果直接在模型上施加重力,模型将产生附加固结变形,特别是对于深厚土层,这种附加变形很大,甚至将改变模型的几何尺寸,不利于后续的分析[13]。因此,在计算模型中需要施加初始地应力,从而模拟土体的实际状态。但在实际工程中,由于测试条件、工程投资等方面的限制,只能对为数不多的点进行土体应力测量。因此,通常通过分析计算的方法获得土体应力。
在分析时,如果不考虑构造应力的影响,土体中的应力场和自重应力场处于相互平衡状态。自重应力场常利用数值计算方法得到。假定弹性材料体内存在初始应力σ0或初始应变ε0,则施加外荷载后的总应力向量

式中: σ是总应力列向量; D为弹性本构矩阵; ε为加载产生的应变。
采用虚位移原理,单元节点力与单元应力关系

式中: Ke为单元刚度矩阵; pe为单元内力的等效节点力向量; δe为单元节点位移向量; BT为应变转换矩阵;为与初始应力有关的刚度矩阵。
系统的平衡方程可变为:

式中: K为系统刚度矩阵; δ为单元节点位移向量; K为系统与初始应力有关刚度矩阵; p为外荷载向量; CeT为位移转换矩阵。
式(6)中,可以把初始应力当作一种特殊的荷载或者把其效应当作初始刚度。假定p为与重力等效的系统的荷载向量,σ0为与重力场相平衡单元的总应力,则式(6)中的节点位移δ=0。这样可以保证附加固结变形被消除,且施加的重力场不会产生新的单元应力,保证单元应力状态与初始条件一致。还有一种近似方法就是从初始应力为零开始先施加重力,得到应力和应变,后续计算减去初始应变得到实际应变。如果将初始应力的效应当作初始刚度,则初始应力或初始应变相当于修正了刚度矩阵,假定p为与重力相等效的系统的荷载向量,则{δ}≠0,这种情况常用于缆索结构初始刚度的描述。本文使用ABAQUS软件自带的地应力平衡模块,把初始应力当做一种特殊的荷载。
2.2 重力的施加方式
开始地震计算时同时考虑重力,重力可以当作不变的荷载施加[10],如式(7)中就是重力。
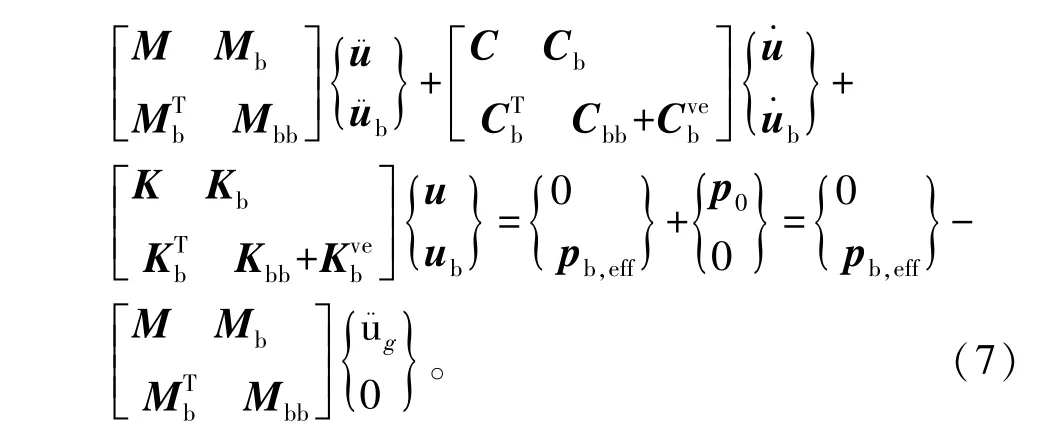
式中: u¨g=[0 0g0 0 0…0 0g0 0 0]Tm×m,m×m表示除了边界以外的自由度;g是重力加速度,由于要与地震同时进行动力计算,所以是时间的函数。
重力作用采用时间的函数有3种形式(见图2),t1和t2是施加的重力时程变为g的时刻,同时,t2是地震开始施加时刻,本文t1取1 s,t2取10 s。方式1为t2时间内重力从0变为g; 方式2为保持g一直不变;方式3为开始t1内重力从0变为g,以后保持g一直不变。这3种施加方式都需要系统实际的或人为假定的阻尼或者耗能机制耗散重力时程的动力效应。在消除动力效应前的反应时间t2内,系统的反应是不真实的,因此,地震施加需要从t2时刻开始或者地震开始前t2时间内进行补零。方式1和方式2是方式3的2个极端,施加方式的优劣可通过数值分析进行评价。
3 重力对地震反应的影响程度
由重力作用和地震作用相互影响,但影响程度以及重力施加的方式需要通过数值计算来评价。
3.1 算例
为评价重力施加方式,本文采用土层厚度为25 m的自由场,均匀土层,土体天然重度为18.6 kN/m3、剪切波速为130 m/s、泊松比为0.30; 模型底部垂直输入水平地震,地震输入采用Anza波,如图3(a)所示。

图2 重力时程施加方式Fig. 2 Different modes of gravity time history
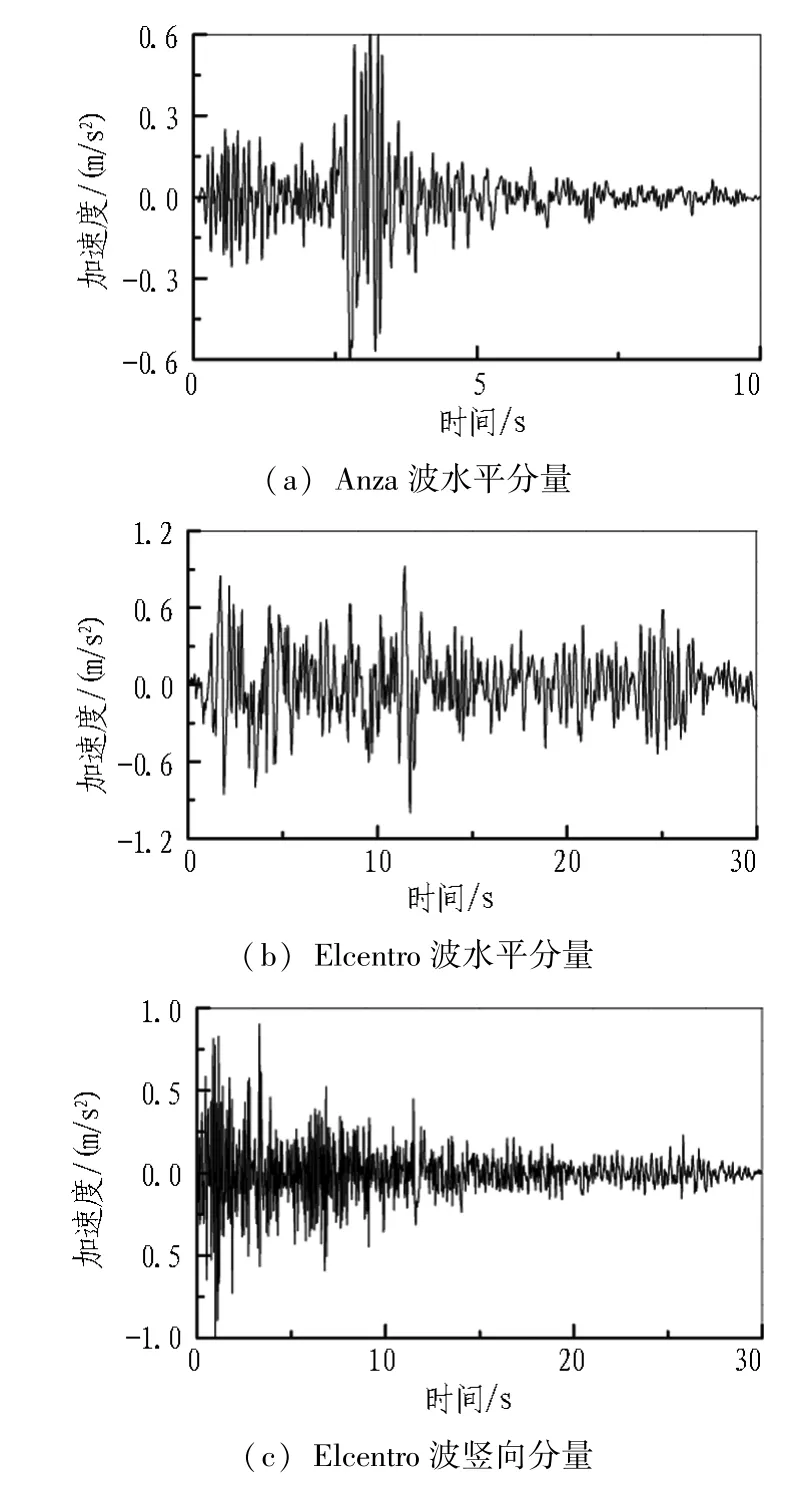
图3 地震波Fig. 3 Earthquake waves
评价重力对地震反应的影响程度时,选取土层厚度为25 m的2种不同性质均匀土层(Ⅱ类场地和Ⅲ类场地),土体、地下结构参数和模型边界条件见图4。在模型底部输入水平和竖向地震动,地震动采用Anza波,见图3(a)(竖向地震动取水平地震动的2/3)以及Elcentro波(分别采用水平分量和竖向分量),如图3(b)和图3(c)所示。
为考虑人工边界处地震波的反射问题,将人工边界设置在离地下结构一定的距离处,使在计算时间内人工边界处的反射波不影响地下结构。因此,本文中计算模型宽度取为1 000 m。

图4 模型示意图Fig. 4 Schematic diagram of model
土体单元和结构单元大小见图4。其中,土体单元不大于λmin/8(λmin为地震波最小波长)[15]。土体阻尼比取5%,土体和地下结构采用平面应变单元,单元厚度为1 m。土体非线性采用Davidenkov模型[16]。
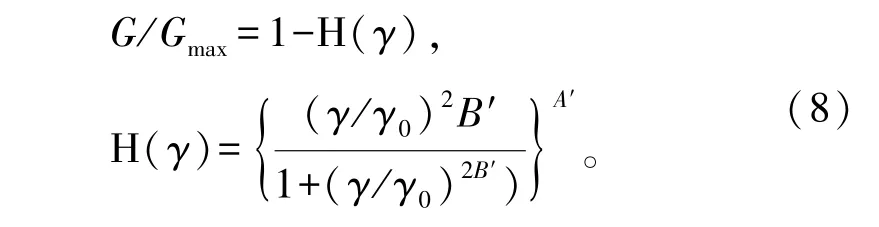
式中:A′、B′和γ0为拟合参数,参数取值如表1所示,按Mashing法则构造相应的滞回曲线;γ为瞬时动剪应变;G为瞬时动剪切模量;Gmax为最大动剪切模量。

表1 拟合参数表Table 1 Fitting parameters
3.2 重力的施加方式评价
选用自由场,设置工况如下: 工况1为有初始应力、线性计算; 工况2为无初始应力、线性计算; 工况3为有初始应力、非线性计算。选取地表A点的水平和竖向位移时程结果进行分析,如图5所示。

图5 位移对比结果Fig. 5 Comparison of displacements
分析图5可知: 1)工况1时,由于地应力平衡后系统有和重力平衡的初始应力,如果开始时施加的重力为0(如方式1和方式3),就会产生一个较大的向上波动位移,且方式1的波动大于方式3; 如果施加重力为1g,则3种方式的竖向位移没有波动。一定时间后再施加地震,方式2和方式3的竖向位移是重合的,方式1有偏差,三者水平位移重合。2)工况2时,方式2相当于突加荷载,竖向位移在开始段波动大;方式1和方式3的波动小,其余规律同工况1。3)工况3时,方式1的竖向位移在开始段波动大,且方式1和方式3竖向位移没有返回到0的位置; 施加地震后3种方式水平位移不重合。综上可得,方式1有误差,不宜使用;方式2和方式3在线性情况下可以使用。但由于进行非线性工况计算不考虑初始应力,很容易造成不收敛,因此,非线性工况需要进行地应力平衡,宜使用方式2。
3.3 重力对地震反应影响程度评价
为考察2种场地(Ⅱ类和Ⅲ类场地)的非线性程度,将水平地震动加速度峰值分别调整为0.1g和0.6g,模型中间位置土体单元应力与应变关系如图6所示。由图6可知,0.6g工况的滞回曲线饱满程度大于0.1g工况,其非线性程度较大;Ⅲ类场地的滞回曲线饱满程度大于Ⅱ类场地,其非线性程度较大。

图6 土体滞回曲线Fig. 6 Soil hysteretic curves
为考察重力的影响,加速度峰值为0.1g时计算线性和非线性2种情况,0.6g时只计算非线性,每种情况采用2种计算方式。方式1是初始地应力、重力、地震同时计算,这种方式理论上精确;方式2是初始应力和重力同时计算,地震单独计算,然后再叠加。
计算结果取图4中A、B、C3个点的竖向和水平位移的平均值,计算地下结构侧墙顶、底点的轴力、剪力和弯矩,其中,轴力、剪力和弯矩的计算公式分别为:
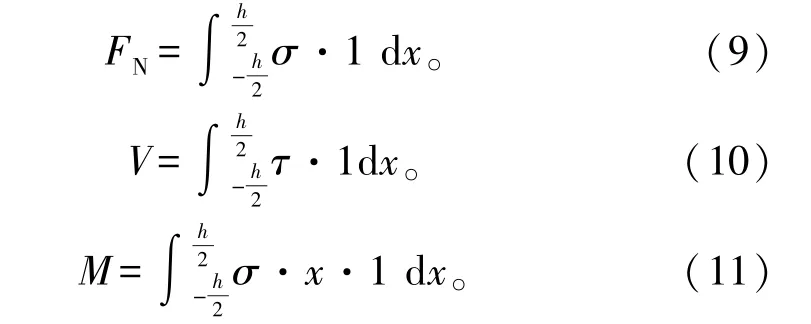
式(9)—(11)中:FN、V、M分别为结构轴力、剪力和弯矩;h为结构壁厚;σ、τ分别为正应力和剪应力; 1为平面应变单元厚度。
以重力施加方式1的结果为基准,评价方式2的结果。为全面地衡量误差,定义3种不同概念的最大值误差,误差定义如下:

式(12)—(14)中:r0(t)为基准模型的反应;r(t)为叠加的反应;tmax为|r0(t)|max对应的时刻; |∗|max为反应量“∗”绝对值的最大值;ε1为r(t)最大值的绝对值与基准模型最大值的绝对值之间的误差,反映的是模型最大反应时的相对误差;ε2为基准模型最大值tmax时刻r(t)的值与对应的叠加模型之间的误差,反映的是基准模型达到反应最大值时刻的相对误差;ε3为模型反应差值最大时的相对误差,代表模型的最大值误差。
计算结果见图7和图8,图中实线代表Ⅱ类场地,虚线代表Ⅲ类场地,Elcentro波(简称E波)结果用实心标签表示,Anza波(简称A波)结果用空心标签表示。

图7 位移误差Fig. 7 Displacement error

图8 内力误差Fig. 8 Internal force error
由图7和图8可知: 线性情况叠加误差较小,非线性情况叠加误差较大,且非线性程度越大,叠加误差越大。其中,对于位移,水平位移的叠加误差小于竖向位移,竖向误差最大值超过100%;Ⅱ类场地叠加误差小于Ⅲ类场地,误差的大小受场地类别的影响。对于内力,误差最大值接近120%,有类似位移出现的规律,但没有位移规律明显,且有非单调情况。
误差结果中ε3总是偏大,而ε1和ε2趋近一致,这一点可以从反应时程图得到更清晰解释。图9示出在Elcentro波作用下,Ⅲ类场地顶点剪力0.6g工况时程和底点弯矩0.1g工况时程曲线。根据ε1、ε2和ε3的定义,由图9可知,基准模型反应最大值时刻,进行叠加的反应与基准模型的反应的差别并非总是最大,而是随时间二者差别有增大的趋势,因此ε3一般总是较大;由于二者时程的趋势基本一致,二者峰值具有一定的同步性,因此ε1和ε2数值接近。
误差结果中还存在ε1、ε2和ε3非单调增加的情况,以ε3为例,取出Anza波Ⅱ类场地底点弯矩和轴力,将非线性0.1g、0.6g的叠加结果、合算结果的差值时程和合算时程进行比较,结果如图10所示。0.1g和0.6g的差值时程的峰值相差不大,但二者合算结果的时程峰值相差较大(2~3倍)。因而,会出现0.6g误差小于0.1g误差的情况。
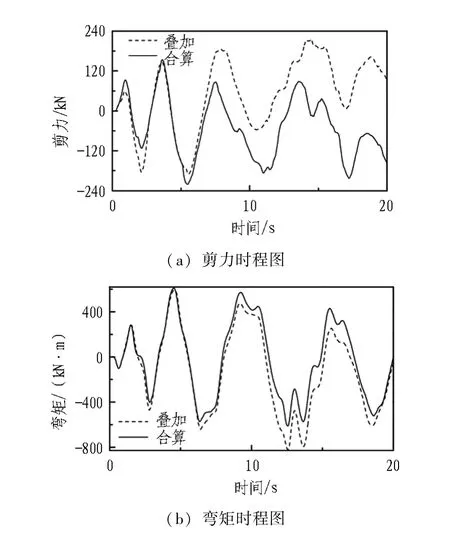
图9 典型时程图1Fig. 9 Typical time history diagram 1
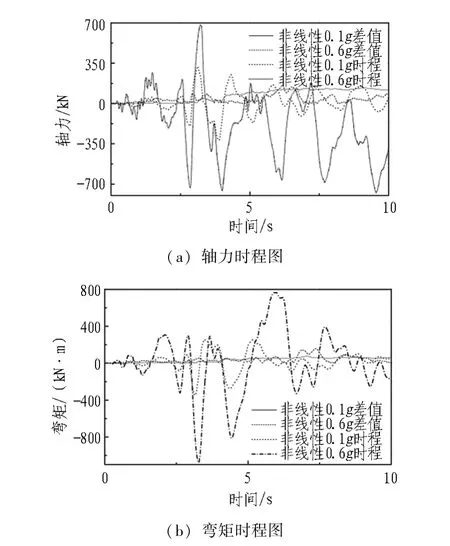
图10 典型时程图2Fig. 10 Typical time history diagram 2
4 结论与讨论
通过理论分析和典型算例数值计算,讨论了地应力、重力施加方式对地下结构的影响,以及重力作用对地下结构地震反应的影响程度,得出以下结论:
1)地下结构进行非线性动力时程计算时,地下结构反应和重力反应分开计算然后叠加产生的水平位移误差较小、竖向位移误差较大,水平位移最大误差超过100%,内力最大误差接近120%。
2)重力和地震作用同时计算时,重力可采用时程荷载的形式施加,并且非线性计算时宜采用一直不变的形式。
3)位移和内力的叠加误差随着土体非线性程度的增加而增大,内力叠加误差并非单调增加,误差范围从小非线性程度的5%到大非线性程度的120%。
4)叠加误差还受场地软硬影响,Ⅲ类场地位移误差大于Ⅱ类场地,Ⅲ类场地的最大误差接近100%,而Ⅱ类场地的最大误差仅达到16%。总体来看,内力误差规律没有位移误差规律明显。
重力对土体中地下结构地震反应的影响还需要进一步研究,比如选取的场地和地震波样本较少,得到的规律不明显,有待设置更多的工况以得到更有规律的结果。
