沉管隧道干坞基坑格形连续墙支护方案评价及其影响因素

2019-05-13林永贵杨春山

隧道建设(中英文) 2019年4期

林永贵, 杨春山

(广州市市政工程设计研究总院有限公司, 广东广州 510060)

0 引言

格形地下连续墙作为自立式新型复合支护结构[1-2],在各类基坑工程中得到了愈来愈多的应用,尤其在无法做内撑且对变形要求严格的沉管干坞基坑工程中。较常规连续墙,格形连续墙表征出的力学行为不尽相同,其应用过程中的受力特性及影响因素值得研究。

当前已有学者[3-5]对格形连续墙的应用力学响应特征进行了研究,然而为数不多的研究均借助数值法,不考虑格形连续墙的实际拉剪接头情况,建立单幅或多幅的连续介质模型,分析格形连续墙的受力变形,存在明显的局限性;同时,格形连续墙为组合式结构,其承载机制尚不明确,影响因素也鲜见报道,对于其完全理解和应用是远远不够的。

基于此,以广州如意坊放射线沉管隧道干坞基坑格形连续墙为例,建立干坞基坑开挖支护过程的三维精细计算模型,揭示格形连续墙受力变形特征,从而开展方案评价及优化,并分析格形连续墙力学特性对不同影响因素的敏感性。

1 工程概况

如意坊放射线系统工程位于广州市荔湾区,是贯穿如意坊和芳村片区南北向交通的大动脉,穿越珠江段采用了沉管法。沉管隧道纵向分6个管节,设计2批预制,采用旁建干坞,位于如意坊立交匝道范围内。干坞基坑底部面积约2.14万m2,坑深14.1 m(见图1)。支护结构在非临江侧采用1.2 m厚地下连续墙+5道可回收锚索,临江侧采用宽9 m、厚1 m的格形连续墙,相邻墙段、幅段间由十字钢板穿孔刚性接头连接。本文旨在研究格形连续墙的应用特性,充分考虑计算规模和可行性,三维计算模型取临江侧的格形连续墙。根据现场勘察资料,干坞基坑场地土层物理力学参数如表1所示,临江侧干坞地质剖面图如图2所示。

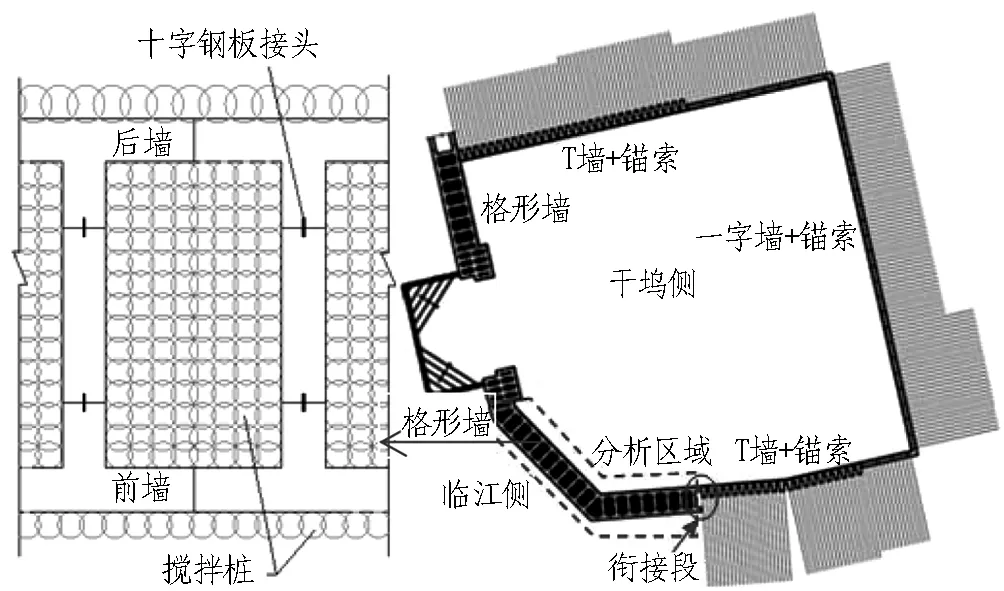
图1 干坞基坑支护平面Fig. 1 Support plane for dry dock foundation pit

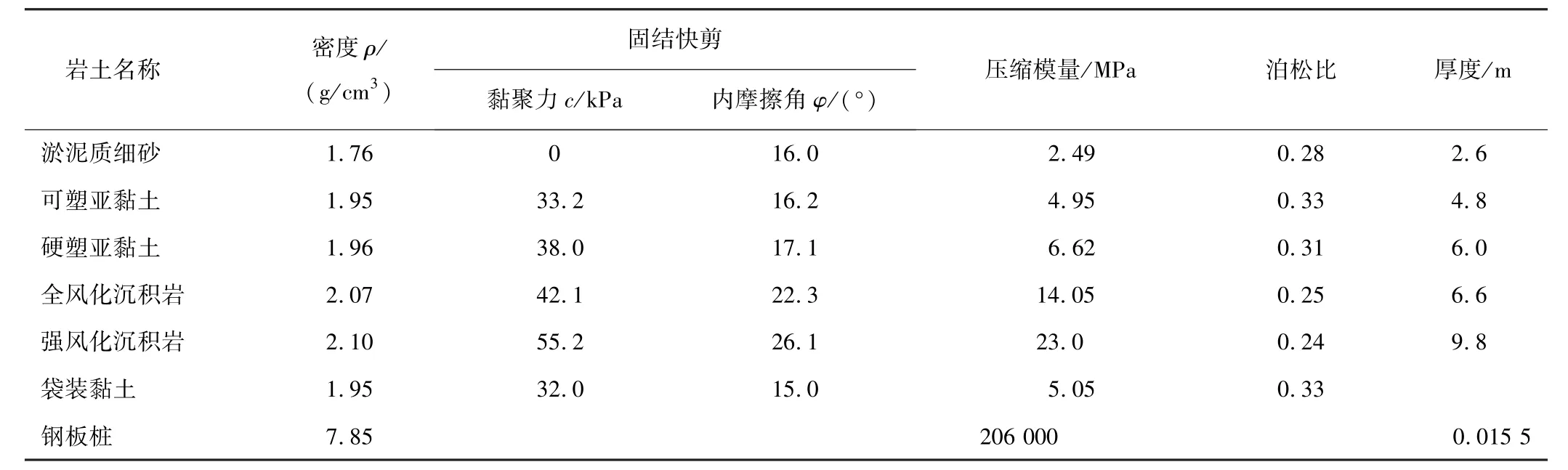
表1 土层结构物理力学参数Table 1 Physico-mechanical parameters of foundation structure

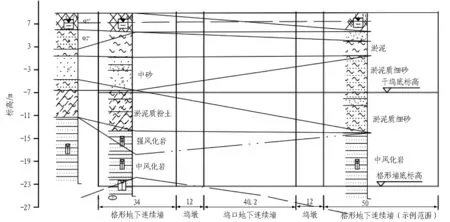
图2 临江侧干坞地质剖面图(单位: m)Fig. 2 Geologic section of the riverside dry-dock (unit: m)

2 格形连续墙方案评价

2.1 评价模型与工况

模型中土体、盖板、连续墙及搅拌桩采用三维实体单元。模型中土体采用理想弹塑性本构模型,遵循Mohr-Coulomb屈服准则,相关结构采用弹性模量。三维整体计算模型如图3所示。模型先生成二维单元,后扩展生成三维模型,计算模型含248 688个单元、167 144个节点。

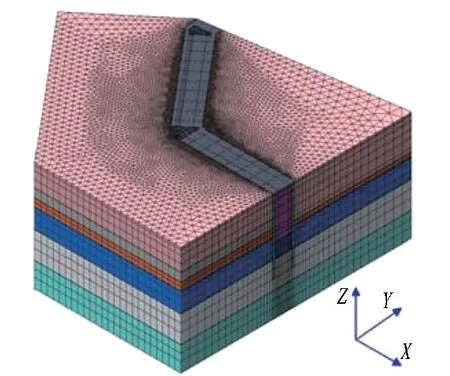
图3 三维整体计算模型Fig. 3 3D calculation model

为了模拟基坑围护结构与土层之间的相对滑移与脱离现象,在两者界面间设置无厚度的Goodman接触单元[6-7],其三维空间的面接触单元在确定外荷载作用下满足式(1)关系。单元的参数: 法向刚度kn、切向刚度ks及转动刚度kθ;N、Q、M表示轴力、剪力及弯矩;Δu为轴向位移,Δv为剪切应变,Δθ为相对转角。

接触单元设置于实体土层与实体维护结构之间,由于实体单元仅存在线位移,因此接触单元位移可以抽象概括为水平与竖向位移,在出现滑移破坏前主要受法向刚度kn和切向刚度ks影响。可通过文献[8]建议的式(2),计算法向与切向刚度:

式中:K、G为接触面两侧材料的体积模量和剪切模量;Δnmin为接触面法向厚度最小的网格宽度。

接触面参数与土体参数、网格尺寸有关,本例kn数量级为(108～1010) Pa/m,ks数量级为(106～107) Pa/m。此次分析包括5个计算工况,具体如表2所示。

2.2 计算结果及分析

格形连续墙位移云图如图4所示。可以看出: 1)受基坑开挖卸载的作用,格形连续墙两侧产生了不平衡的压力,促使墙体产生指向基坑内的位移; 2)墙体呈现出典型的悬臂变形特性,最大侧移为18.85 mm,出现在墙体的顶部,符合一般的变形认识。

表2 计算工况Table 2 Calculation conditions

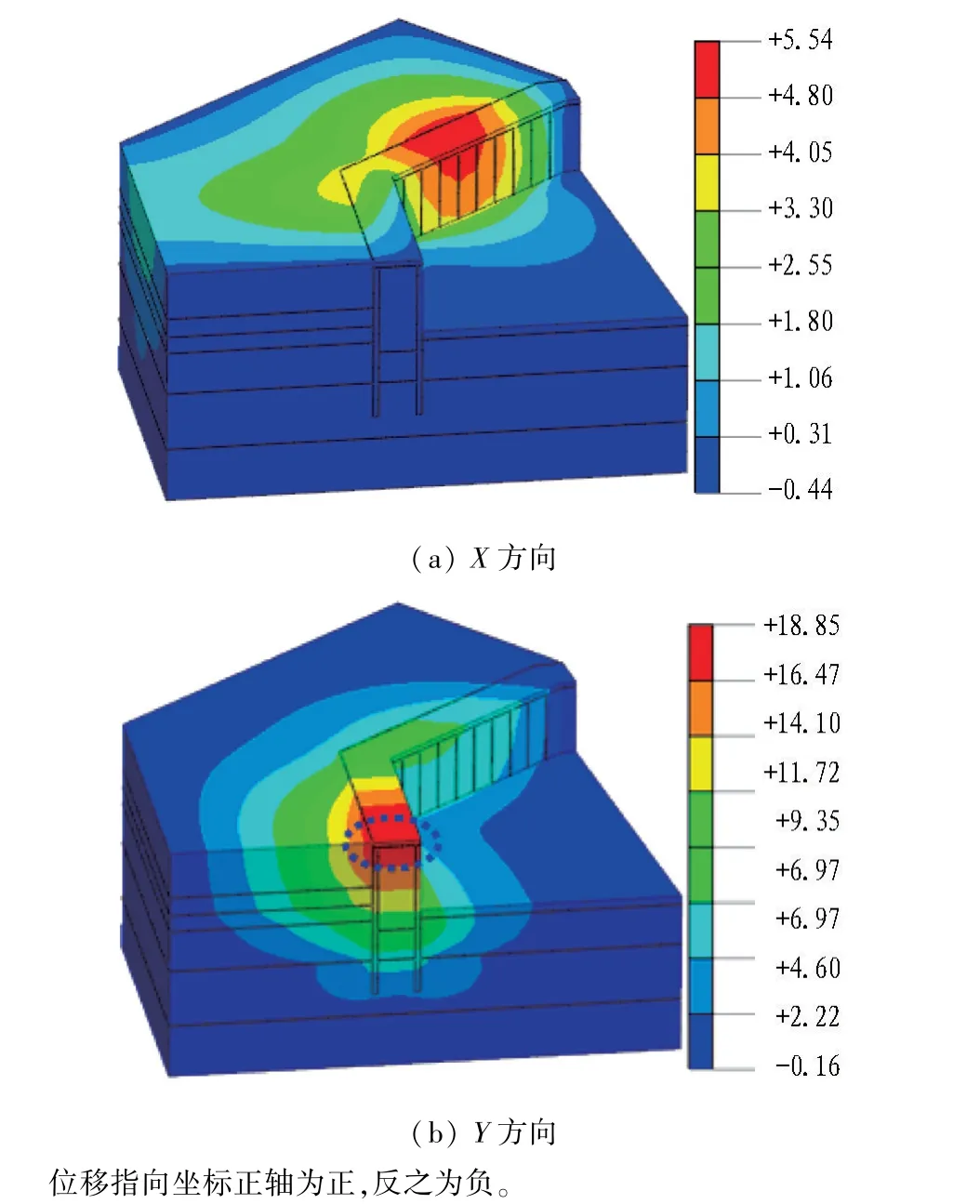
图4 格形连续墙位移云图(单位: mm)Fig. 4 Displacement of cellular diaphragm wall (unit: mm)

在该项目干坞基坑支护方案设计过程中,为了保证计算结果的可靠性,合理指导设计实践,开展了格形连续墙支护的平行计算。与另一高校平行计算结果进行对比分析(见图5),以验证本文计算模型的合理性。由图5可知,两者位移总体趋势较为吻合,说明本文所用计算模型具备一定的可靠性,平行计算位移值总体更大,因为平行计算结果采用了二维模型,空间刚度更小。

由图4和图5还可以看出: 1)基坑格形墙体最大位移小于规范[9]要求的一级基坑的位移限值,说明基坑支护体系能够满足稳定性要求; 2)基坑2种支护形式衔接部位(见图1)位移存在较明显的突变,有必要对原有支护方案格形连续墙支护、T形墙+锚索支护衔接位置局部加强。

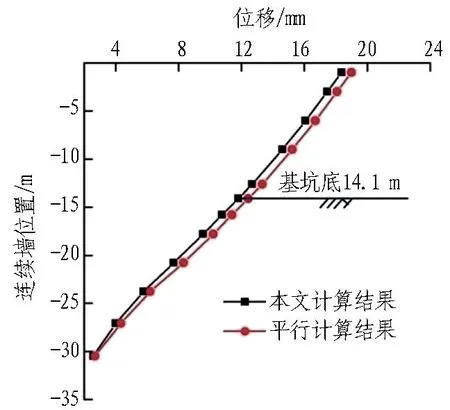
图5 本文与平行计算结果对比Fig. 5 Comparison between the result of this paper and parallel calculation result

格形连续墙应力云图如图6所示。可以看出: 1)因格形连续墙阳角两侧均向坑内移动,导致盖板转角位置出现了应力集中,产生了较大的拉应力,最大应力为14.25 MPa,超出了盖板混凝土的抗拉强度,局部开裂并由此可能引发盖板向两侧延伸,发生渐进破坏; 2)针对应力集中的局部区域,在原有设计方案的基础上,增加预埋受拉钢筋,以此抑制裂缝的形成和发展。

图6 格形连续墙应力(单位: kPa)Fig. 6 Stress of cellular diaphragm wall (unit: kPa)

2.3 格形连续墙支护特性影响因素

格形连续墙支护特性内因影响因素包括墙体嵌入深度、盖板尺寸、接头刚度及搅拌桩加固等,外因影响因素包括土层刚度和外部扰动程度等。考虑到土层刚度相对固定,且连续墙嵌入深度较常规连续墙方案类似,故着重探讨土层刚度与墙体嵌入深度以外的其他因素对格形连续墙支护特性的影响。以基本模型为基础,保证其他参数不变,改变单个参数以考察其影响程度。

2.3.1 混凝土盖板的影响

不同格形连续墙盖板厚度对应的墙体位移结果如图7所示。为了分析盖板厚度对格形连续墙墙体位移的影响,取0.8、0.9、1.0、1.1、1.2 m 5种厚度盖板进行计算。由图7可以看出: 1)盖板厚度对格形连续墙位移有较明显的影响,尤其对坑底以上悬臂端地下墙位移影响较为显著; 2)盖板厚度影响格形连续墙的整体刚度,盖板越厚,地下墙的整体刚度越大,墙体的位移越小; 3)5种不同盖板厚度下计算得到地下墙顶端位移为16.5～20 mm,从工程实施的角度上均处在允许的位移变形范围内,而且随着盖板厚度逐渐加大,对格形连续墙位移的影响逐渐减弱。工程实施过程中应结合实际需求,综合安全性和经济性选取设置合理的盖板厚度。

图7 不同盖板厚度对应的位移Fig. 7 The displacements to different plate thickness

2.3.2 搅拌桩加固的影响

为了考察格形连续墙前、后墙体间搅拌桩加固对基坑开挖变形的影响,设置不同搅拌桩加固范围,包括初始设计方案(17 m加固)、坑底上下3 m和6 m及不加固4种方案,计算得到图8所示不同搅拌桩加固范围对应的墙体位移结果。可以看出: 1)基坑开挖格形连续墙位移受前、后墙间(内格)搅拌桩加固范围影响很细微,究其原因是该项目连续墙主要表现为底部嵌入岩层的悬臂支挡结构,墙体位移取决于侧向水土压力、嵌岩深度及支挡结构的空间刚度; 2)在水土压力和嵌岩深度一定的情况下,提高支挡结构的空间刚度是至关重要的,而前、后墙间搅拌桩加固在一定程度上提高了墙间土层的强度与刚度,但相对于格形连续墙支护体系来说,贡献是非常细微的,因此墙体变形受到的影响甚微。

图8 不同搅拌桩加固范围对应的位移Fig. 8 The displacements to different range of cement mixing pile reinforcement

2.3.3 接头刚度的影响

实际施工过程中,格形连续墙接头质量往往难以保证,导致连续墙整体刚度不足,影响整体支护。为模拟上述工况,设置不同的连接墙段、幅段连接接头刚度,分析接头刚度折减对连续墙整体承载的影响。不同格形连续墙接头刚度对应的墙体位移结果如图9所示。可以看出: 随着墙间连接接头刚度的折减,格形连续墙围护结构整体性变差,空间刚度减小,位移逐渐增大,当刚度折减到一定程度时趋于稳定,因为此时格形连续墙结构变为叠合结构,各组成部分近乎单独承载。