一种快速计算溶解油气比的工程实用方法

2019-05-13席永钊刘安琪赵金洲张烈辉李蜀涛赵向阳

天然气工业 2019年4期

魏纳席永钊刘安琪赵金洲张烈辉吕鑫李蜀涛赵向阳

1.“油气藏地质及开发工程”国家重点实验室·西南石油大学 2.中国石油川庆钻探工程公司地质勘探开发研究院3.中海油研究总院有限责任公司 4.中国石化石油工程技术研究院

0 引言

天然气溶于原油后，可以显著地改变原油的物性参数（黏度、密度、体积系数等）。因此，天然气（包括氮气、二氧化碳）在原油中的溶解参数被广泛应用于油藏工程、油气资源评价和储量评价[1-2]。大量天然气溶解于原油中，改变了原油的物性及流变性[3]。对于天然气在原油中的溶解度计算，目前主要有诺谟图、雷萨特相关关系式、斯坦丁关系式以及瓦兹奎兹—贝格斯公式[4-5]，而诺谟图、雷萨特相关式都需要查图版，斯坦丁关系式和瓦兹奎兹—贝格斯的精确度不是很高，因而在实际工程中，需要一个精确度高并且计算方便的公式来处理工程上的溶解油气比问题，对研究井筒流动的快速精确计算有着积极意义[6-7]。为此，笔者提出了一种快速计算溶解油气比的工程实用方法。

1 溶解油气比工程计算法

脱气原油是相对于溶气原油而言的。通常情况下，把常压（工程标准状况）储罐中的原油称为脱气原油，当原油中溶解有天然气且处于比大气压高的压力状态时，可称之为溶气原油[8-9]。溶气原油的溶气量、密度和黏度等物性随压力、温度条件而变化[10]。1 m3脱气原油在某一压力和温度下能够溶解的天然气量（折算成工程标准状况下的体积）称之为天然气在原油中的溶解度，或称溶解油气比[8,10]，常以Rs表示。

雷萨特（Lasater）在实验数据的基础上，给出了求Rs的关系式[6]：

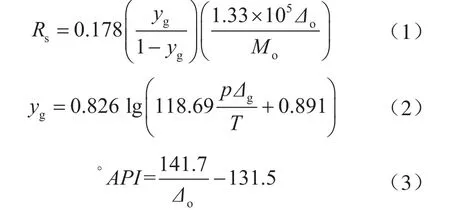
式中Rs表示溶解油气比；yg表示天然气的摩尔分数；°API表示美国石油协会（American Petroleum Institute，缩写为API）相对密度[11]；Mo表示脱气原油摩尔质量，g/mol，先由式（3）求出°API相对密度，然后查图1得到；p表示绝对压力，MPa；T表示温度，K；Δo表示脱气原油对水的相对密度；Δg表示天然气对空气的相对密度。

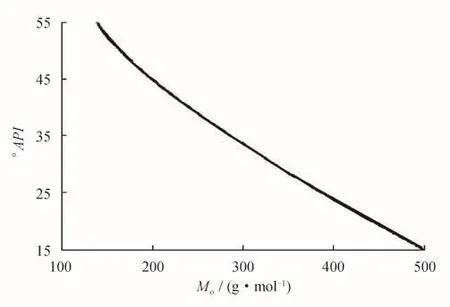
图1 °API－Mo关系曲线图

从雷萨特相关式来看，其方法是首先根据Δo运用式（3）得到°API值，然后再查图1得到Mo，其次根据已知p、Δg及T通过式（2）得到天然气的摩尔分数（yg），最后在式（1）中得到Rs。而我们知道在实际的工程计算中，查图版是很不方便的。鉴于雷萨特关系式的准确度相对较高，因此以雷萨特的相关式为基准，根据°API－Mo的图版，在其数据线上选取了100个数据点，将°API－Mo的图版转换成Mo与°API的函数关系式，最大精度地用函数来代替图版。从图1中选取了100个数据点作为数据拟合的基本点，如表1所示。

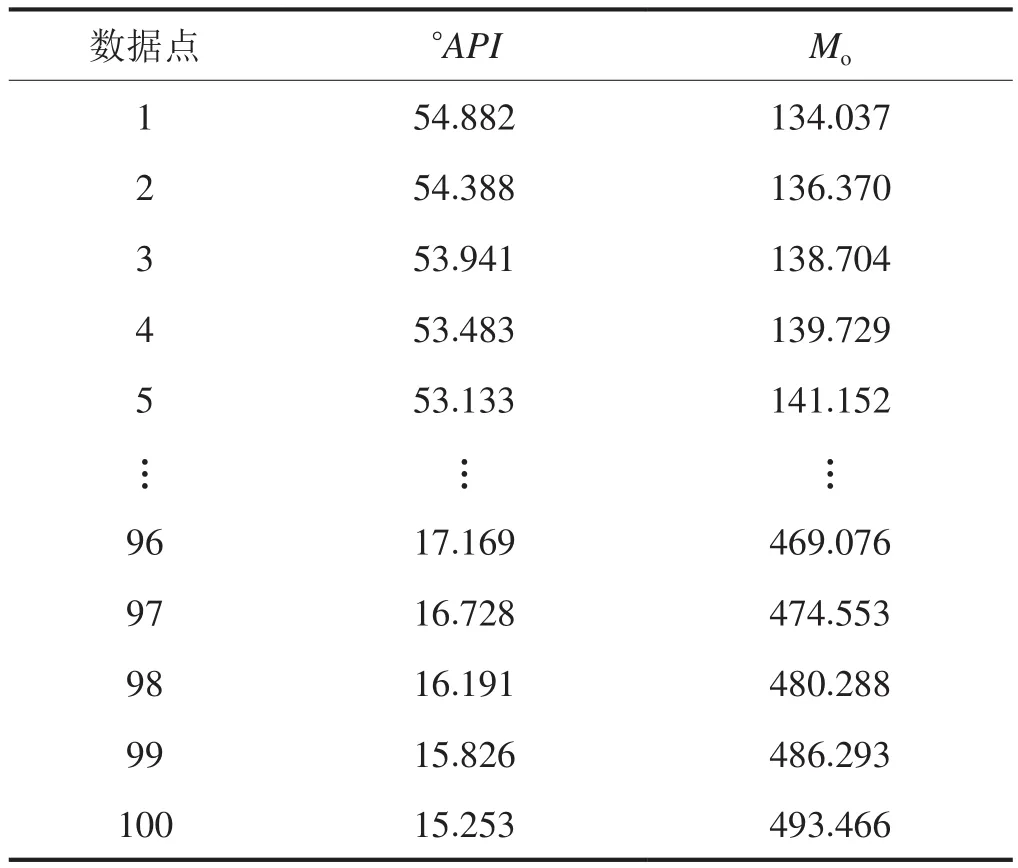
表1 从图1中选取的100个数据点列表

通过对表1中100个数据点进行拟合，得到最大精度的拟合曲线如图2所示，从图2可以得到Mo和°API的函数关系，其函数公式为：其拟合的相关性系数达到了99.98%。因此该拟合程度非常的高。

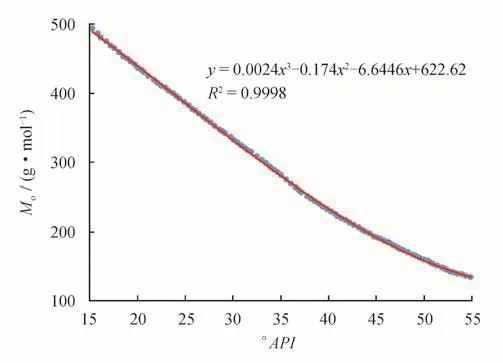
图2 100个数据点拟合的Mo－°API关系曲线图

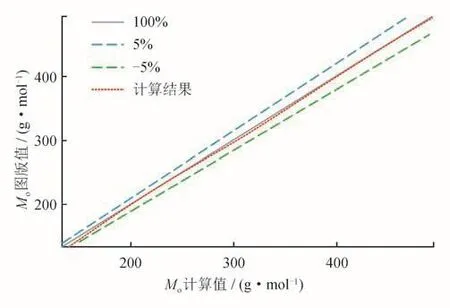
图3 拟合函数和查图版所得数据的对比评价图

如图3所示，再将在图版上得到的100个数据和将100个数据代入拟合曲线所得到的数据进行对比，其拟合的结果精度都在±5%以内，表明所采用的拟合函数可以高精度地表示原有的°API－Mo图版。

为了进一步验证拟合的曲线可以完全表示图版，在图1的关系曲线上取10个不同于上述100个数据的点，利用查图版法得到Mo和函数关系得到的Mo在相同°API下的结果进行对比和误差分析，结果如表2所示。从表2中可以看出，通过函数关系得到的Mo的相对误差最高不超过4%，平均相对误差介于0.1%～1.0%，再一次证明了该拟合函数可以用来表示原图版曲线，符合油田上应用计算的要求。应用这种简便的方法计算出Mo随°API的变化规律，计算结果与查图版得到的结果相对误差很小，证明了该方法可以用来计算Rs的有效性和可行性。

根据得到的Mo－°API关系曲线，将式（3）°APIΔo的关系式代入，得到Mo与Δo的关系式如下：

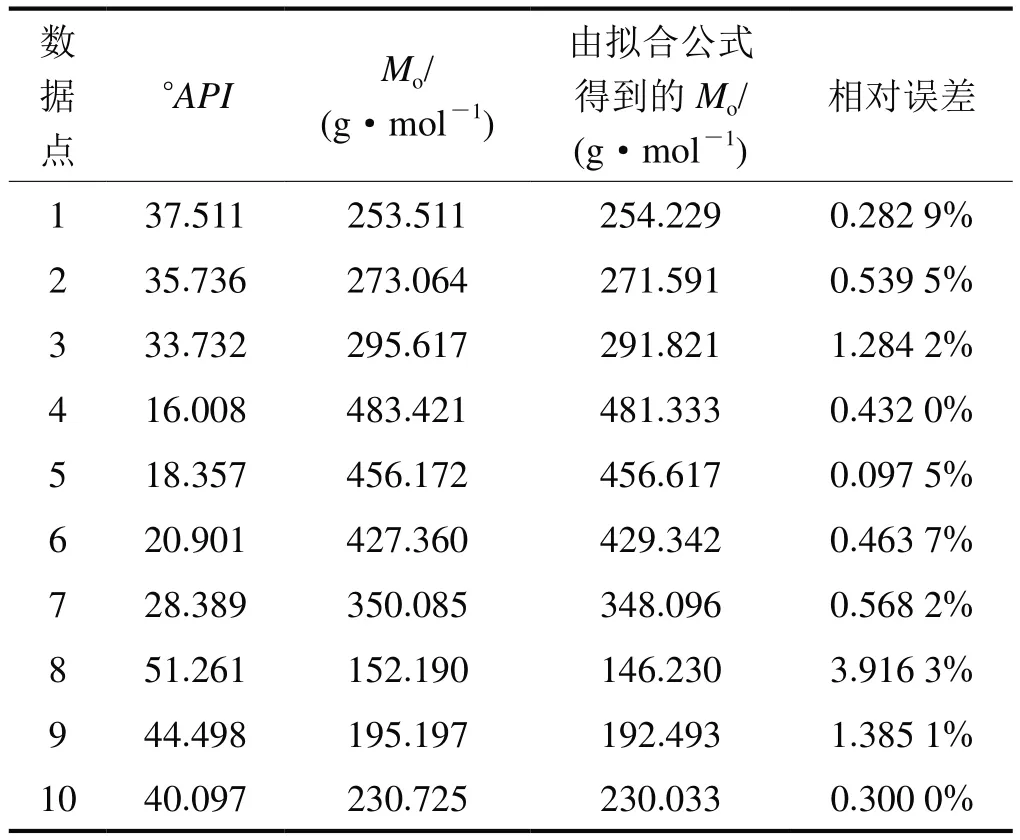
表2 不同方法得到的脱气原油摩尔质量对比表

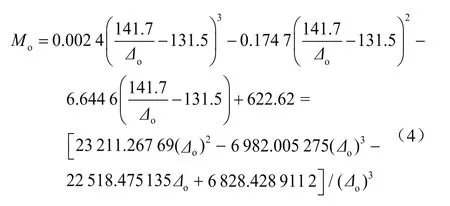
根据已知的Δo代入公式（4）中得到Mo，再根据已知的p、T以及Δg代入式（2）中求得到yg，再把得到的Mo和yg代入式（1）中即可得到Rs。

当然，为了进一步的方便，将式（2）和式（4）代入式（1）中，得到一个改进版的雷萨特相关式，该关系式结合了原有的雷萨特的相关式，将其中的图版模块用函数关系式进行代替，并且将繁琐的一个个公式进一步推导成一个溶解油气比与绝对压力、温度、脱气原油的相对密度和天然气相对密度的关系式，省去了中间一些不必要的计算过程。在工程中，可以直接根据已知的数据，在计算机上直接运用相关的关系式，输入所需要的4个已知参数便可快速、准确地求得溶解油气比，其关系式如下：

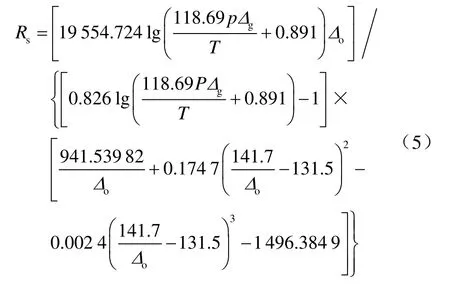
对比原雷萨特相关式，所得到的计算溶解油气比的模型简单了许多，需要的参数也仅有4个，而雷萨特模型需要由已知脱气原油对水的相对密度Δo值，由式（3）计算出°API，后查图版得到脱气原油摩尔质量Mo，由已知的绝对压力、温度、天然气的相对密度代入式（2）得出天然气摩尔分数，最后将天然气摩尔分数、脱气原油对水的相对密度和脱气原油摩尔质量代入式（1）得到溶解油气比的值。而所得到的关于溶解油气比的新模型，只需要将绝对压力、温度、脱气原油的相对密度和天然气的相对密度代入一个公式中便可得到溶解油气比，大大减少了无关参数和中间繁琐的计算环节，且避免的查图版的不方便性，由于该模型是溶解油气比与绝对压力、温度、脱气原油的相对密度和天然气的相对密度的直接函数关系，可以直接对溶解油气比的影响因素进行分析。

2 溶解油气比影响因素分析

对比原来的雷萨特相关式，新模型不仅可以一步到位计算溶解油气比，而且可以从公式中反映出各个参数是如何影响溶解油气比的变化，相比原有的雷萨特相关式繁琐的迭代简单了许多，下面对各个参数进行分析。

2.1 压力对溶解油气比的影响规律

根据式（2）确定yg时，绝对压力的取值一般必须大于0.4 MPa时，雷萨特公式才能使用[12]，因此所选取绝对压力值的范围为0.5～3.0 MPa，温度取293.15 K，脱气原油对水的相对密度取0.8，天然气对空气的相对密度取0.6。图4所示为溶解油气比随绝对压力的变化规律。图4表明溶解油气比随着绝对压力的增大而增大。由图4可以看出，溶解油气比与绝对压力基本上呈线性关系，即溶解油气比与绝对压力是正相关的关系。

绝对压力分别取1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa和3.0 MPa，温度取293.15 K，脱气原油对水的相对密度取0.8，天然气对空气的相对密度取0.6，由原有的雷萨特关系式可以得到°API为45.625，通过查原雷萨特的°API－Mo关系曲线图版得出脱气原油摩尔质量Mo为188.313 g/mol，将所有已知数据代入雷萨特相关式得出绝对压力分别为1.0 MPa、1.5 MPa、2.0 MPa、2.5 MPa和3.0 MPa时的溶解油气比值如图4中所示红点。对比由原雷萨特模型计算的5个点和新模型所得到的曲线，可以看出原模型计算的点基本都在曲线上，误差很小，并且新模型得到的关系式可以连续地反映溶解油气比与各个参数之间的变化规律。

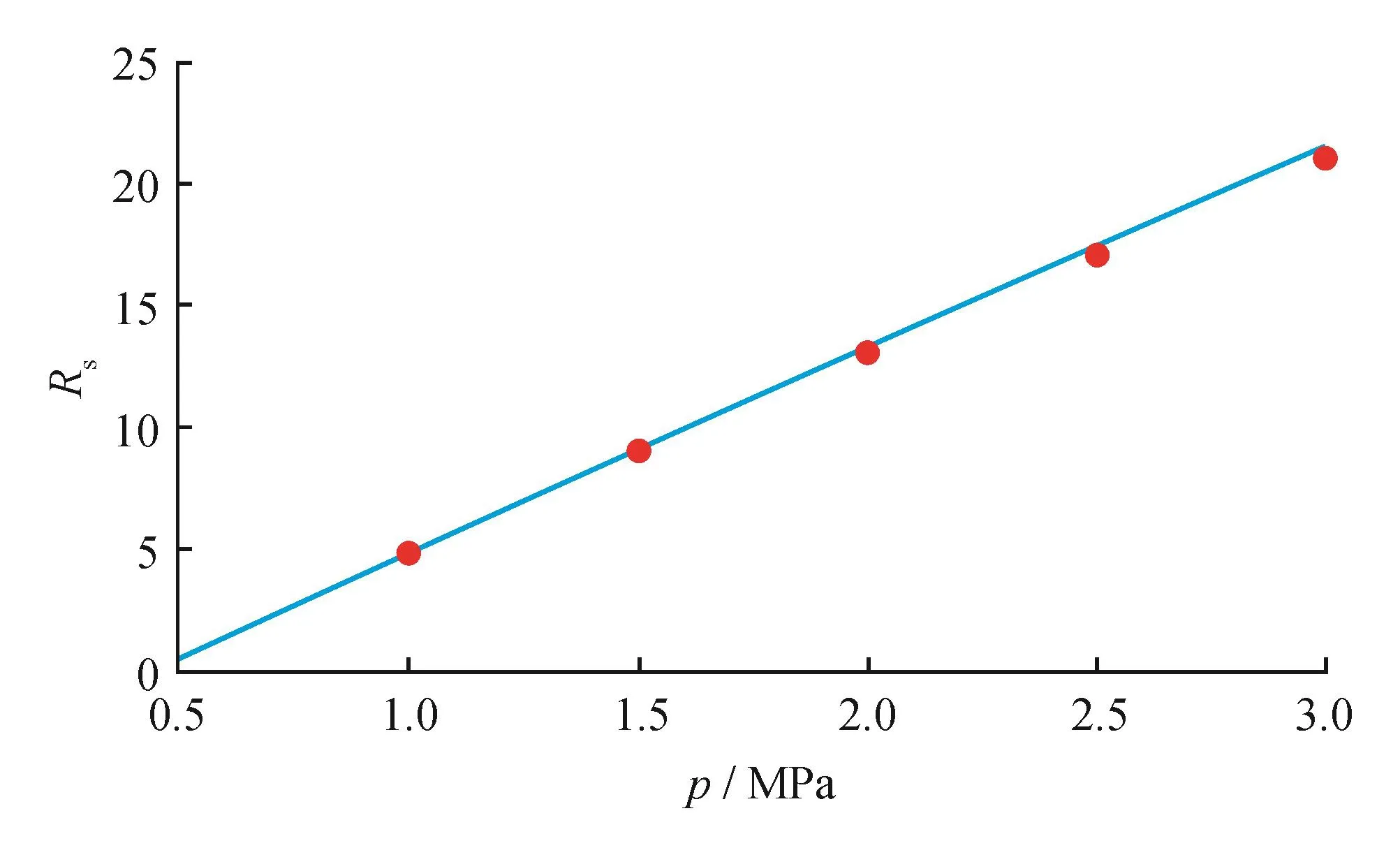
图4 溶解油气比随压力的变化图

2.2 温度对溶解油气比的影响规律

在研究温度对溶解油气比的影响规律时，所选取的温度范围为273.15～333.15 K，绝对压力取1 MPa，脱气原油对水的相对密度取0.8，天然气对空气的相对密度取0.6。图5所示为溶解油气比随温度的变化规律。图5显示随着温度的不断增加，溶解油气比在不断降低。由图5可以看出，溶解油气比与温度也基本上呈线性关系，即溶解油气比与绝对压力是负相关的关系。

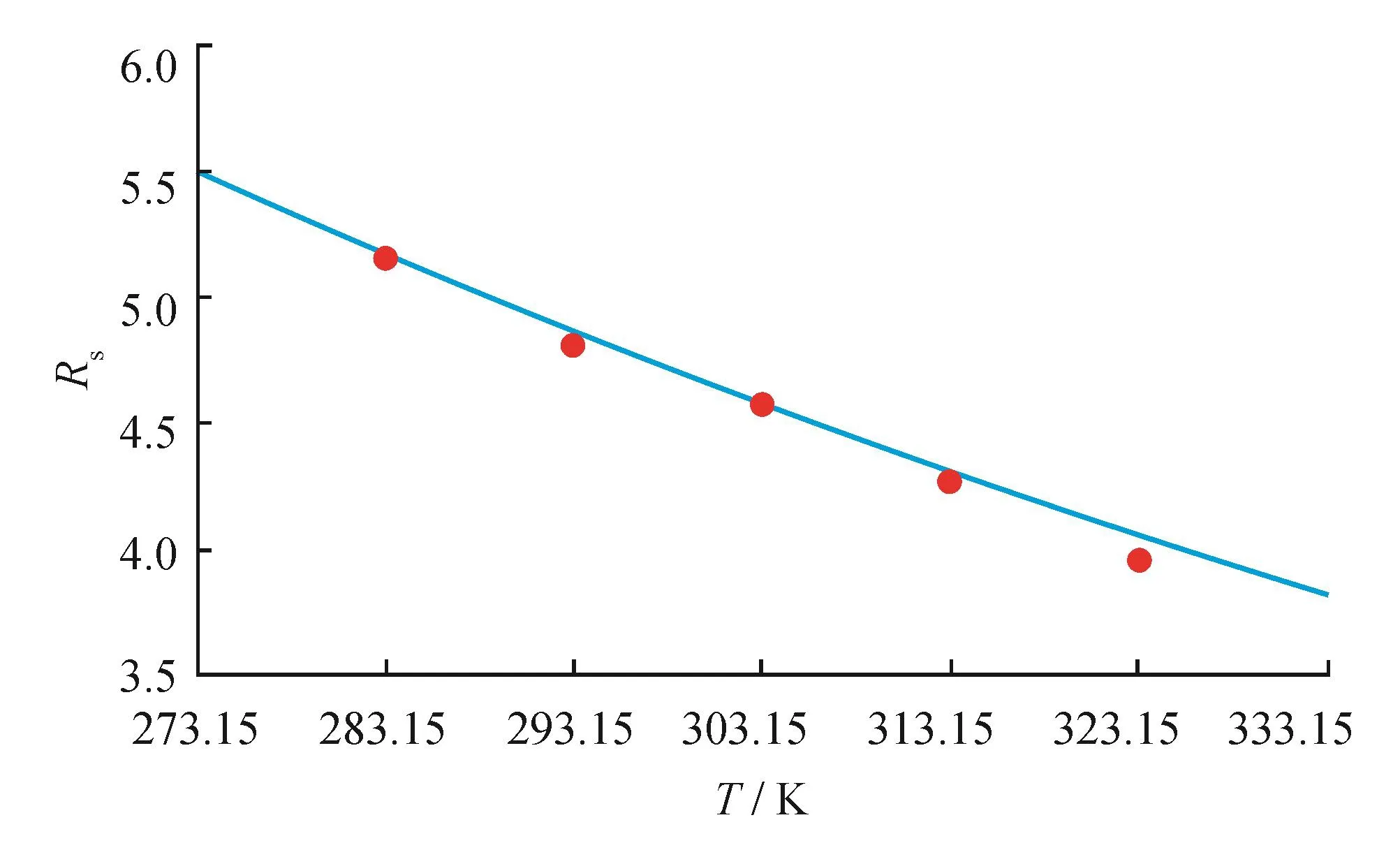
图5 溶解油气比随温度的变化图

温度分别取 283.15 K、293.15 K、303.15 K、313.15 K和323.15 K，绝对压力取1 MPa，脱气原油对水的相对密度取0.8，天然气对空气的相对密度取0.6，此时的°API同样为45.625，通过查原雷萨特的°API－Mo关系曲线图版得出脱气原油摩尔质量Mo为188.313 g/mol，将所有已知数据代入雷萨特相关式得出温度分别为283.15 K、293.15 K、303.15 K、313.15 K和323.15 K时的溶解油气比值，如图5中所示红点。对比由原雷萨特模型计算的5个点和新模型所得到的曲线，可以看出原模型计算的点与曲线的误差很小。

2.3 脱气原油相对密度对溶解油气比的影响规律

通过式（3）可以得到°API与脱气原油对水相对密度Δo的换算关系式，而°API相对密度的取值范围为0～100[13]，因此根据式（3）便可得到Δo的取值范围为0.611～1.076。对Δo所采用的研究范围为0.6～1.0，绝对压力取1 MPa，温度取293.1 K，天然气对空气的相对密度取0.6。图6所示为溶解油气比随脱气原油相对密度的变化规律，结果表明溶解油气比随着脱气原油相对密度的增大先增大后减小。当脱气原油相对密度小于0.73时，随着脱气原油相对密度的增大，溶解油气比也随之增大；当脱气原油相对密度大于0.73而小于1时，随着脱气原油相对密度的增大，溶解油气比却在不断减小。

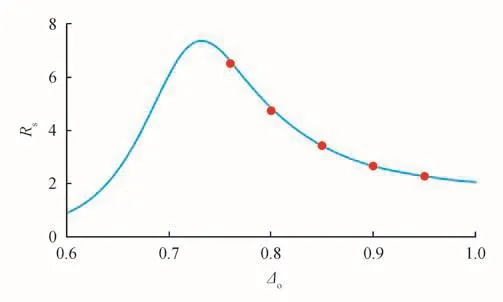
图6 溶解油气比随脱气原油对水的相对密度的变化图

脱气原油对水的相对密度分别取0.76、0.80、0.85、0.90和0.95，绝对压力取1 MPa，温度取293.15 K，天然气对空气的相对密度取0.60，此时的°API由于脱气原油对水的相对密度Δo的不断变化也不断变化，分别由式（3）求出对应的°API值，再通过查原雷萨特的°API－Mo关系曲线图版得出对应的脱气原油摩尔质量Mo，将所有已知数据代入雷萨特相关式得出脱气原油对水的相对密度分别取0.76、0.80、0.85、0.90和0.95时对应溶解油气比值，如图6中所示红点。从所得到的曲线对比来看，由原雷萨特模型得到的5个点基本都在曲线上，证明了该曲线的可行性。

2.4 天然气相对密度对溶解油气比的影响规律

目前认为天然气的相对密度一般介于0.58～0.62[14]或介于0.50～0.70[15]。因此对天然气相对密度采取的范围介于0.5～0.7，绝对压力取1 MPa，温度取293.15 K，脱气原油对水的相对密度取0.8。图7所示为溶解油气比随天然气相对密度Δg的变化规律，从图7看出随着天然气对空气的相对密度增大，溶解油气比也增大。从图7的趋势来看，天然气的相对密度和绝对压力对溶解油气比的影响类似，两者均与溶解油气呈正相关关系。

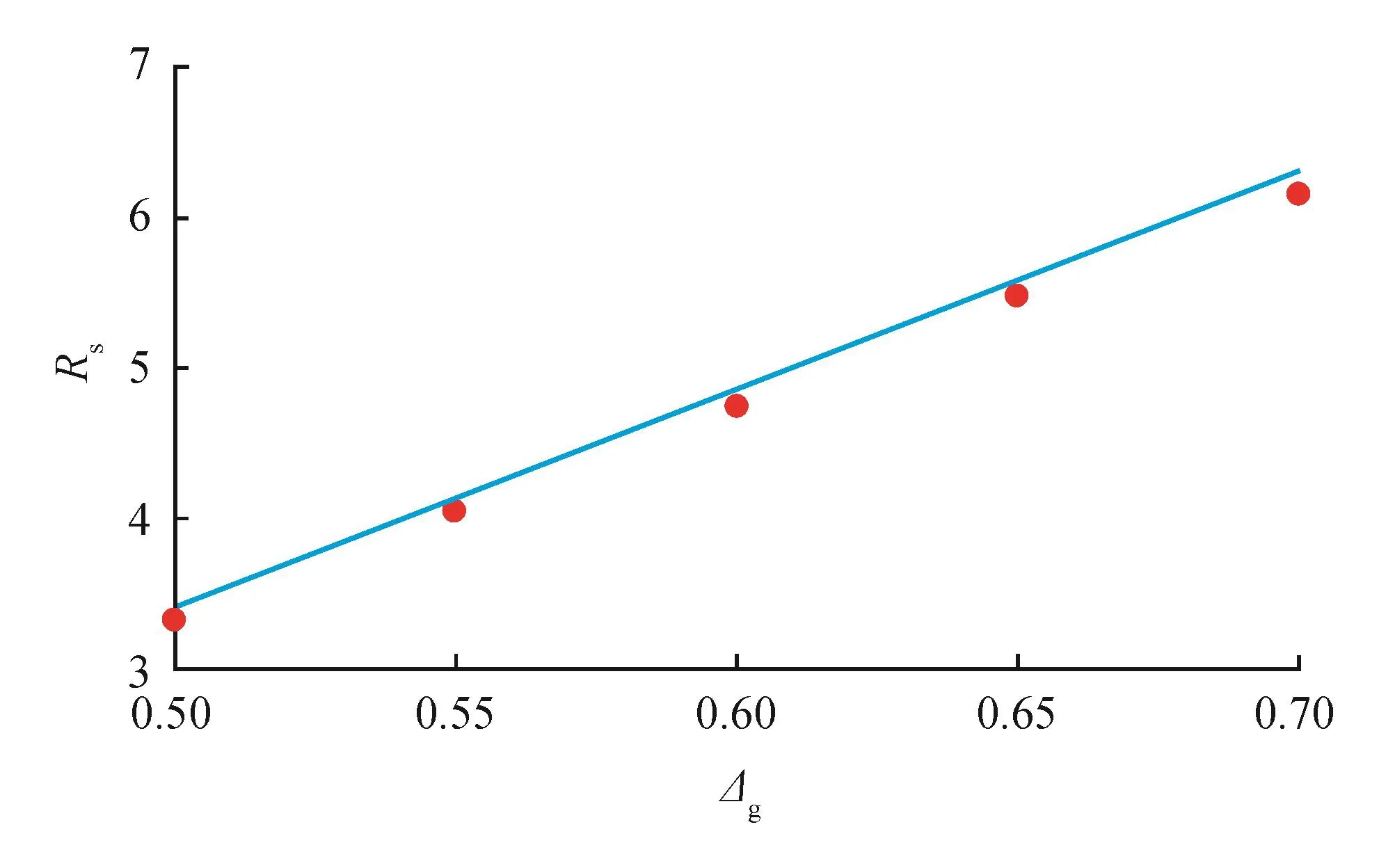
图7 溶解油气比随脱气天然气对空气相对密度的变化图

天然气对空气的相对密度分别取0.50、0.55、0.60、0.65和0.70，绝对压力取1 MPa，温度取293.15 K，脱气原油对水的相对密度取0.8，此时°API同样为45.625，而脱气原油摩尔质量Mo也同样为188.313，将所有已知数据代入雷萨特相关式得出天然气对空气的相对密度分别取0.50、0.55、0.60、0.65和0.70时所对应溶解油气比值，如图7中所示红点。对比图7中的红点和曲线，由原雷萨特模型得到的5个点在曲线上下可允许的范围波动，由此证明所得到的曲线可以用来表示原雷萨特模型。