不同气候条件下平板太阳能集热器动态热性能的解析

四川大学建筑与环境学院■李皓月 龙恩深 肖雪飞

0 引言

近年来，太阳能热利用系统在我国的发展越来越快，太阳能集热器的热性能对太阳能热利用系统至关重要。平板太阳能集热器常用于低温太阳能热利用系统中，在多数工程中，平板太阳能集热器全年平均效率直接根据经验取值为0.25～0.5[1]。集热效率是评价太阳能集热器集热性能的一个重要指标，平板太阳能集热器瞬时效率受外界气象条件的影响较大，各因素对其耦合影响难以量化分析。工程设计中，平板太阳能集热器的集热效率的计算方法常采用《太阳能供热采暖工程技术规范》(下文简称“《规范》”)附录C[2]中，基于集热器实际测试参数的效率公式，用当地月或年平均环境参数计算。虽然该方法较为简单、方便，但由于在实际运行中，集热器每天的参数必定在变化，因此，若要模拟实际工况，该方法不够精确。

在利用数学模型及计算机模拟研究集热器热性能影响因素方面，大部分学者仅研究固定条件下的稳态模型，且更侧重于集热器结构参数或运行参数对效率的影响，但集热器瞬时效率受环境因素的影响较大，且在实际运行时，环境参数及自身运行参数会不断变化。因此，需要利用数学模型并结合气候条件等精确模拟实际工况下的集热器全年效率。

本文通过建立一种可结合环境气象数据等参数计算一段时间内集热效率动态分布的数学模型，研究不同气候区平板太阳能集热器的集热效率差异，并与工程设计中的常用方法进行比较，以期在研究各因素对集热效率的影响的同时，能为工程实例中平板太阳能集热器平均效率的选取提供参考。

1 数学模型

本模型基于太阳能集热器稳态效率计算的推导过程[3]，通过对集热器前后不同时刻进、出口温度的预测，建立平板太阳能集热器的集热效率动态模型，且李皓月等[4]已用实验验证了本模型的准确性。

1.1 稳态效率模型

集热效率是规定时间内吸收的有效能与入射在集热器表面上的太阳总辐射通量的比值。图1为平板太阳能集热器的典型结构示意图。

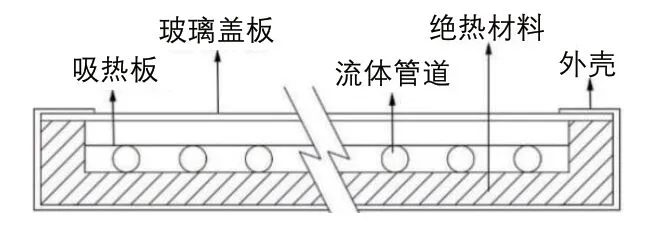
图1 平板太阳能集热器典型结构示意图

根据能量守恒定律，入射在集热器表面上的太阳总辐射通量等于有效能、光学损失、热损失之和。已考虑光学损失的入射在集热器表面的太阳总辐射通量用公式表示即为：

式中，AC为采光面积，m2；α为吸热板吸收率；τ为透明盖板透过率；IT为入射在集热器表面上的辐照度，W/m2；Qu为工作介质吸收的有效能，W；Qlh为集热器热损失，W。

式中，UL为总传热系数，W/(m2·K)；Tp,m为吸热板平均温度，℃；Ta为环境温度，℃。

将式(2)代入式(1)可得：

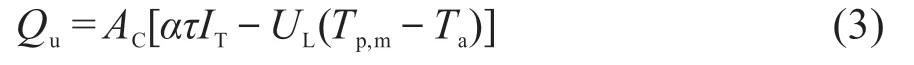
集热器的热损失由顶部、底部和边缘3部分的热损失组成。因此，总传热系数UL可表示为：

式中，Ut、Ub、Ue分别为集热器顶部、底部和边缘的热损失系数，W/(m2·K)。

根据Klein[5]提出的经验公式，可将Ut的误差控制在±0.3W/(m2·K)以内，即：

式中，N为玻璃层数；hw为玻璃盖板与环境之间的对流换热系数，W/(m2·K)；εc为玻璃发射率，取0.88；εp为吸热板发射率；σ为玻尔兹曼常数，σ=5.67×10-8W/(cm2·K4)。f=(1+0.892hw-0.1166hwεp)(1+0.07866N)；e=0.43(1-100/Tp,m)。β为集热器倾斜角，(°)，在 0°＜β＜70°时，c=520(1-0.000051β2)；在 70°＜β＜90°时，c用β=70°计算。

Ub的计算公式为：

式中，kb为底部绝热材料的导热系数，W/(m·K)；L为底部绝热层厚度，mm。

Ue的计算公式为：

由于测定Tp,m存在困难，因此，引入集热效率因子F′[6]。将式(3)变为式(8)，热损失与流体局部的流体温度Tf和Ta之差成正比，即：

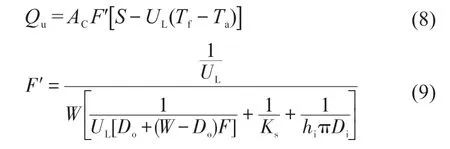
式中，S为吸热面吸收的太阳幅射量，W/m2，Qu=ατIT；Ks为焊缝导热系数，W/(m·K)；F为翅片效率；W为翅片宽度，mm；Do为流道外径，mm；Di为流道内径，mm；hi为流体与管壁间的对流换热系数，W/(m2·K)。

在Tf中，集热器入口温度Tf,i最易测定，引入热迁移因子FR，可将有效能表示为：

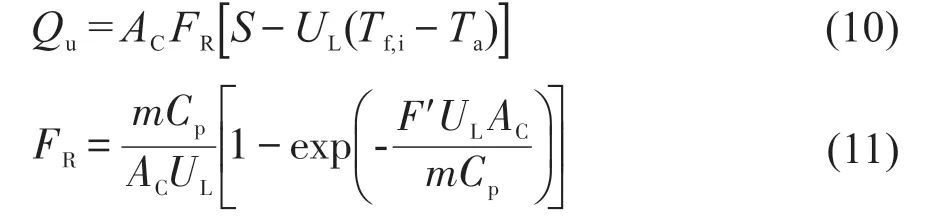
式中，m为通过集热器的质量流量，kg/s；Cp为水的定压比热容，J/(kg·℃)。

则集热器稳态效率η为：

1.2 动态效率模型

集热器在实际运行时，运行参数、环境参数均在不断变化。为更接近实际工程情况，作者在以上稳态工况下的瞬时效率数学模型的基础上加以改进，针对集热系统构建了可以计算全天或全年不同时刻的集热器动态效率模型。

当研究对象是整个太阳能集热系统时，按照能量守恒定律，Qu与管路损失系数ξ的乘积等于系统中蓄热装置(如蓄热水箱)所得的热。计算n个小时内的有效能Qu，即：

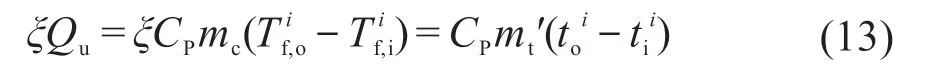
式中，Qu可由式(10)算出；mc为集热器质量流量，kg/h；Tf,o为集热器出口温度，℃；Tf,i为集热器入口温度，℃；mt为水箱中水的质量，kg；to为水箱出口温度，℃；ti为水箱入口温度，℃；ξ为管路损失系数，根据工程经验取值；上角标“i”代表第i时刻。

考虑管路损失后，将集热器温度和水箱温度联系起来，可得：

利用式(12)～式(15)，可将第i时刻和第i+1时刻的瞬时模型联系起来，得到不同时刻的不同瞬时效率，并可研究更长的任意一段时间内集热器瞬时效率的动态分布。

若要研究全年集热器平均效率η′，则可用全年每时刻有效能及全年每时刻所得到的太阳总辐射通量之和的比值来计算[3]，即：

综上所述，改进后的模型可在单一固定条件的瞬时效率模型的基础上形成一个瞬时效率的动态分布模型，模拟一段时间内的实际参数变化。若将全年气象数据代入模型，设置集热器结构参数、运行参数，即可得出全年总效率和瞬时效率的动态分布。

2 集热效率的解析

为了研究外界条件对集热效率的动态影响，将上述模型分别置于代表严寒地区、寒冷地区、温和地区、夏热冬冷地区的4个不同气候区的典型城市——哈尔滨、北京、昆明、成都，比较在相同参数设定下不同城市的平板太阳能集热器的集热效率差异。为简化分析，假设模型为直流的集热系统。表1给出了模型中设定的平板集热器的结构参数。

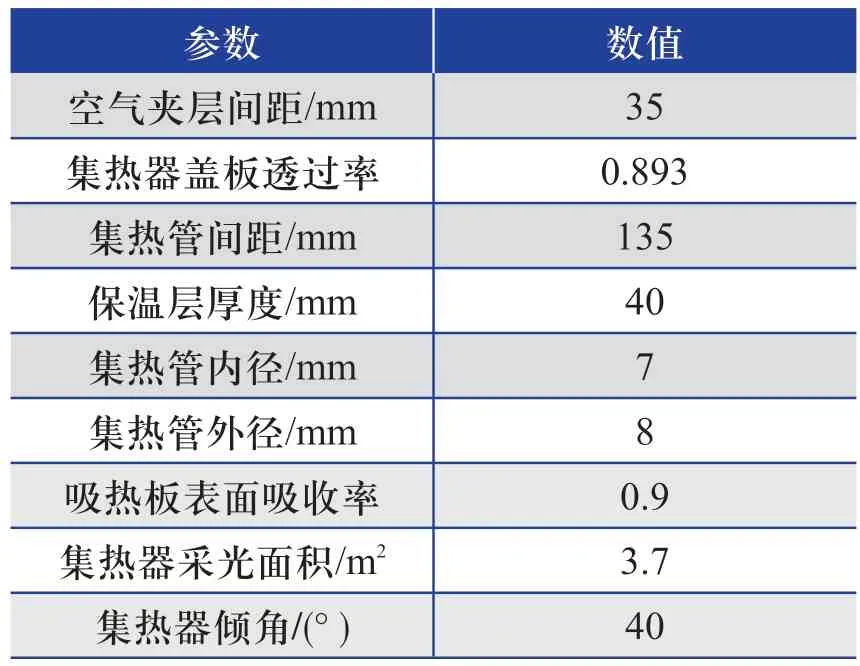
表1 模型中平板集热器的结构参数

集热器底部与边缘保温材料均为聚胺脂整体发泡保温、玻纤棉保温。吸热板材料为铝，流体介质为水，质量流量为0.05kg/s，太阳辐照度、环境温度、环境风速均为DesT气象数据库所给的全年逐时数据。集热器第一时刻入口温度设定为20℃。

在模型中，用式(16)计算出各城市的集热器年平均效率模拟结果，如表2所示。

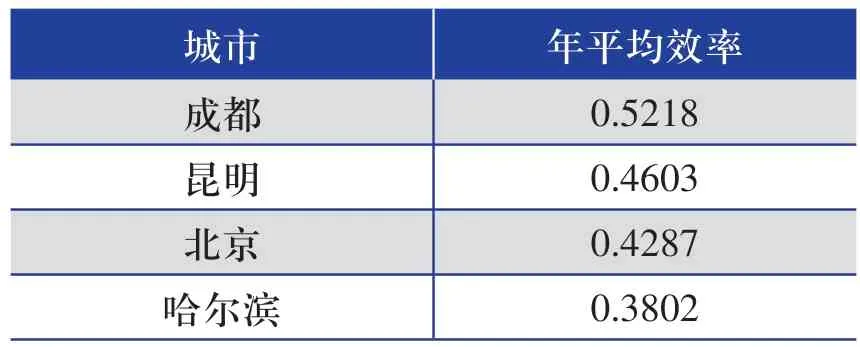
表2 各城市的集热器年平均效率模拟结果

从表2可以看出，在上述参数设定下，成都年平均效率最大，为0.5218；哈尔滨最小，为0.3802；在其余参数设定相同时，各城市的年平均效率按从大到小排列为：成都＞昆明＞北京＞哈尔滨。因环境温度、太阳辐照度、环境风速都会不同程度地影响效率，它们之间的耦合作用难以量化分析，但在模型中输入实际气象参数，可模拟实际集热器系统运行，以分析不同城市的集热器平均效率差异。

为进一步分析不同城市的集热器全年效率分布的特点，由前文所述模型，可得到各城市逐月效率的模拟结果分布，如图2所示。

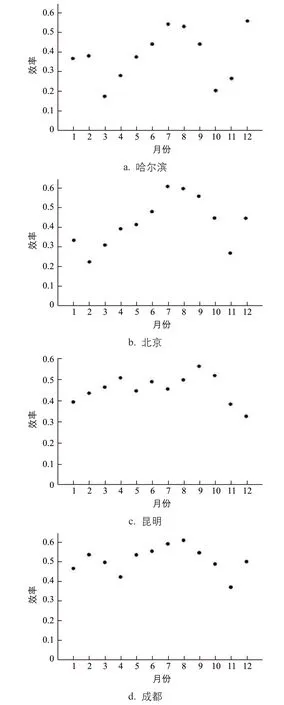
图2 各城市的集热器逐月效率分布

从图2可以看出，其余参数设定相同时，不同城市全年12个月的效率分布有较大差异：

1)北京、哈尔滨冬季环境温度较低，集热器热损失较大，冬季及过渡季的效率明显比夏季小，其效率分布呈明显“W”型，即在过渡季效率比冬季低。主要原因在于集热器的集热效率受环境温度和集热器入口温度等因素耦合影响，在其他因素不变的情况下，环境温度越低，效率越低；集热器入口温度越低，效率越高。将本模拟结合实际可知，集热器入口温度并非固定，而是由上一时刻集热或放热的状态决定的。在冬季环境温度较低的城市，在晚上散热、放热后，早上集热器入口温度较低；过渡季，环境温度较冬季更高，但集热器入口温度也更高，在两因素耦合作用下，部分城市的集热效率在过渡季比冬季低。

2)成都、昆明全年的环境温度相比北京、哈尔滨较高，环境风速较小，因此，太阳辐照度对效率的影响程度较大，其全年效率分布并无大起大落。

为研究全年环境温度、集热器入口温度对集热器瞬时效率分布的影响，进一步解释“W”型的原因，图3给出了各城市全年8760h的瞬时效率随各时刻集热器入口温度与环境温度之差(Tf,i-Ta)的变化图。

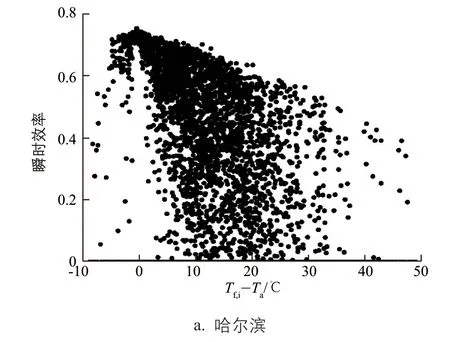
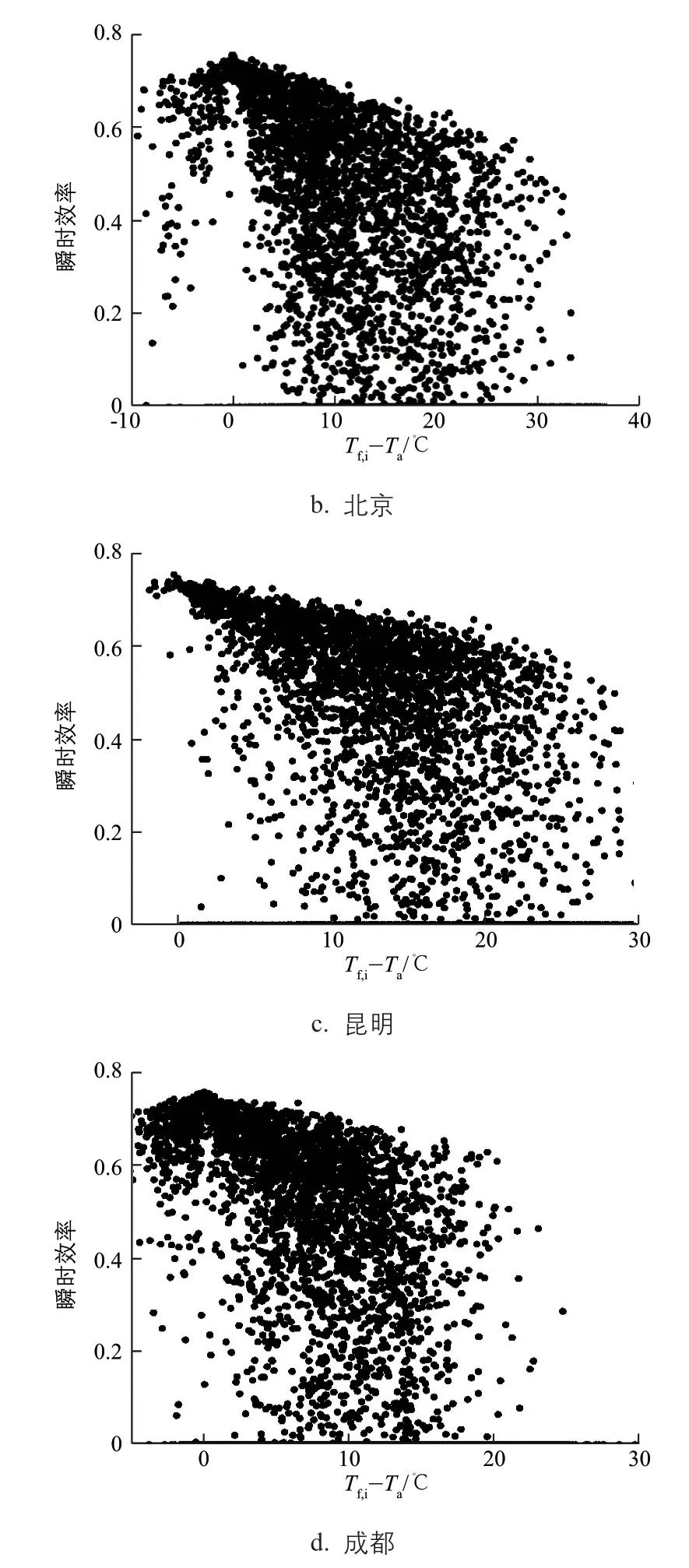
图3 瞬时效率随温差的变化规律

从图3可以看出，总体来看，全年温差按从大到小排列为：哈尔滨＞北京＞昆明＞成都。出现温差为负的原因是在全年一些太阳辐照度较小的时刻，集热器中流体介质吸收的太阳总辐射通量较少，因此，当环境温度也较低时，流体介质散热便大于得热；由于散热较大，导致流体在下一时刻入口温度较低，则出现少数温差为负的情况。可以看到，成都太阳能资源较不丰富，则在4个城市中温差小于零的时刻较多；同时也说明了在温差为负时，该城市是不适合使用平板集热器集热的。在温差为正时，随着温差增大，瞬时效率降低，散点图呈锥状发散。从锥形上部边界的斜率可以看出，温差对瞬时效率的影响为哈尔滨＞北京＞昆明＞成都，其原因是北京、哈尔滨全年环境温度较低，集热器热损失较大，且环境温度对集热器入口温度也有影响，所以从温差对瞬时效率的影响趋势来看，北京、哈尔滨比昆明、成都更明显。

为研究全年太阳辐照度对集热器的集热效率分布的影响，图4给出了各城市全年瞬时效率随全年各时刻太阳辐照度的变化图。

从图4可以看出，瞬时效率的散点图趋势类似一个弧形，其中，成都的图形较收敛，弧形最明显。由此可知，随着太阳辐照度的增大，集热器的集热效率随之增高。图形发散程度为哈尔滨＞北京＞昆明＞成都，其原因是成都、昆明的全年环境温度与北京、哈尔滨相比较高、风速较小，因此散热较小，瞬时效率主要受太阳辐照度的影响；而在北京、哈尔滨，环境温度等对瞬时效率的影响较大，因此，太阳辐照度对瞬时效率分布的影响趋势没有成都、昆明明显。

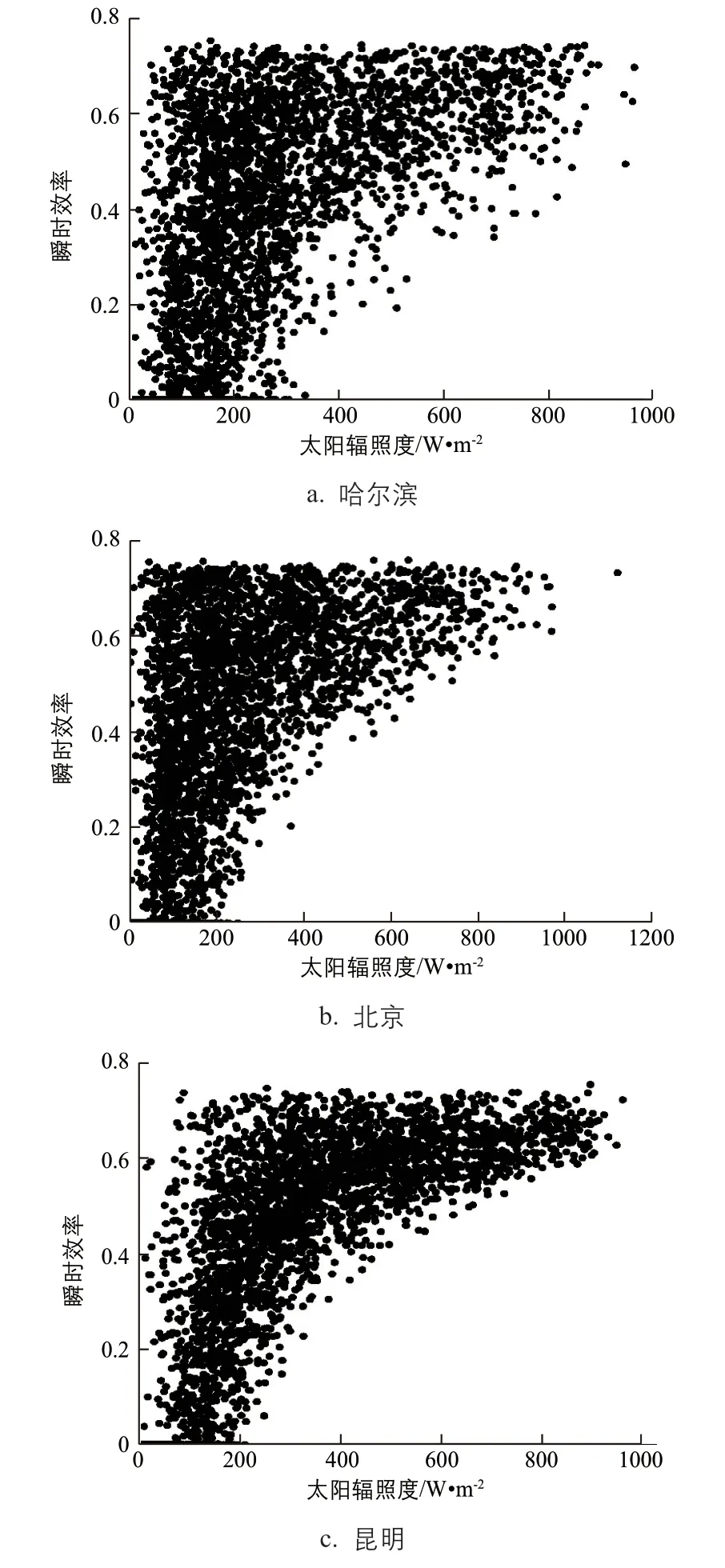
图4 瞬时效率随太阳辐照度的变化规律

因此，在不同气候条件下，集热器在实际运行中，并非环境温度越低，瞬时效率越低。在某些年平均气温较低的城市，全年瞬时效率分布因集热器入口温度和气象条件的耦合影响呈“W”型；但在这些城市，冬季平均集热效率比过渡季高并不意味着平板集热器适合在该地的冬季使用；相反，由于这段时间内集热器中流体温度低，获得的可有效使用的能量极少，应停止运行。

3 与常用方法比较分析

为更加深入地分析本模型，将本模型与工程设计中的常用方法进行比较。常用方法即采用《规范》附录C[2]给出的计算集热效率ηa的公式，采用厂家所给的集热器实际测试参数计算：

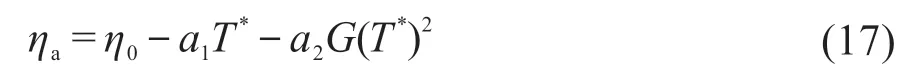
式中，T*为归一化温差，(m2·K)/W，T*=(Tf,i-Ta)/G；G为总太阳辐照度，W/m2；η0为无热损时的瞬时效率；a1、a2为集热器热损失系数。η0、a1、a2的值均由厂家实际测试得出。

T*的计算在季节蓄热和短期蓄热太阳能供热采暖系统(下文简称“短期蓄热系统”)中取值不同，本模型模拟工程为短期蓄热系统。在《规范》中，计算对象为短期蓄热系统时，ta取当地12月的平均室外环境温度。其中，Hd为当地12月集热器采光面上的太阳总辐照度的月平均日辐照量，kJ/m2；Sd为当地12月平均每日的日照小时数，h。无论系统为全年运行还是仅在冬季运行，在《规范》中均需用上述计算值来设计。

现用与上节相同的参数设定，将计算的4个城市的集热器年平均效率的模型模拟结果和《规范》计算结果进行比较，如图5所示。

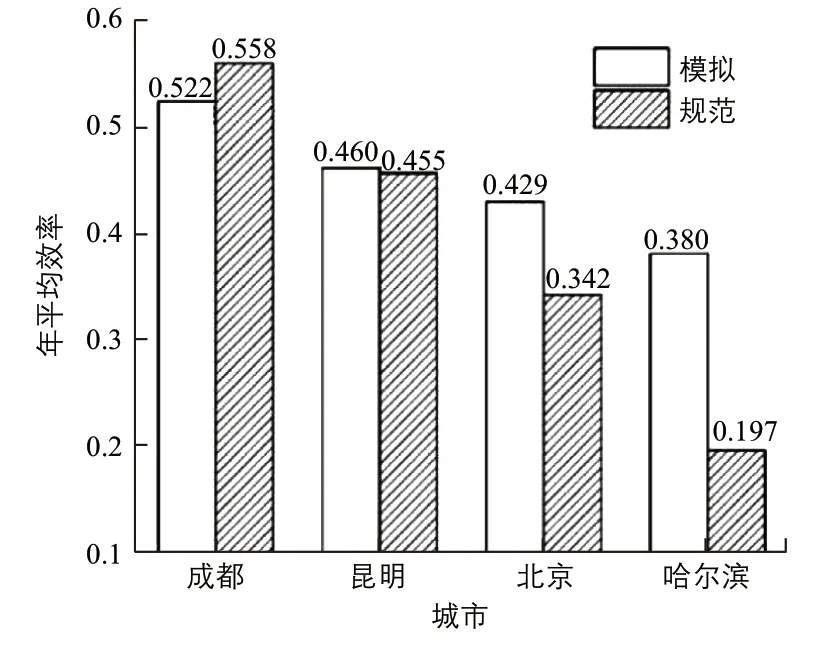
图5 各城市年平均效率的模型模拟结果与《规范》计算结果比较图

从图5可以看出，模拟结果和《规范》计算结果稍有差异，成都的模拟结果比《规范》计算结果约低3%，而昆明、北京、哈尔滨的模拟结果偏高。造成二者差异的原因主要是：

1)在短期蓄热系统中，《规范》所用环境参数为12月的平均值，而模拟是根据工程模拟了全年的实际运行情况，得到的为全年运行时的平均效率。

2)《规范》直接利用厂家给出的集热器实际测试参数，而国内标准[2]对参数测试的试验条件有严格规定，如集热器采光面上的太阳辐照度不小于700W/m2，试验期间总太阳辐照度变化不大于±50W/m2，周围环境空气速度不高于4m/s等[7]；但在集热器实际运行过程中，环境参数是不断变化的，测试条件的特殊性导致得出的结果存在局限。而本模型将集热器系统运行参数和环境参数均考虑在内，模拟了实际的运行情况。

在工程中，计算集热器全年效率大多是为了在太阳能集热系统的设计中计算集热器面积，当集热效率计算值偏低时，集热器面积设计值则会偏大，这样就会在某些时候造成“大马拉小车”的局面，造成能源的浪费。

用模型模拟集热器冬季运行时的平均效率(以日平均温度不满足连续5天超过10℃为条件划分冬季)，而《规范》计算结果不变。模拟结果和《规范》计算结果的比较如图6所示。

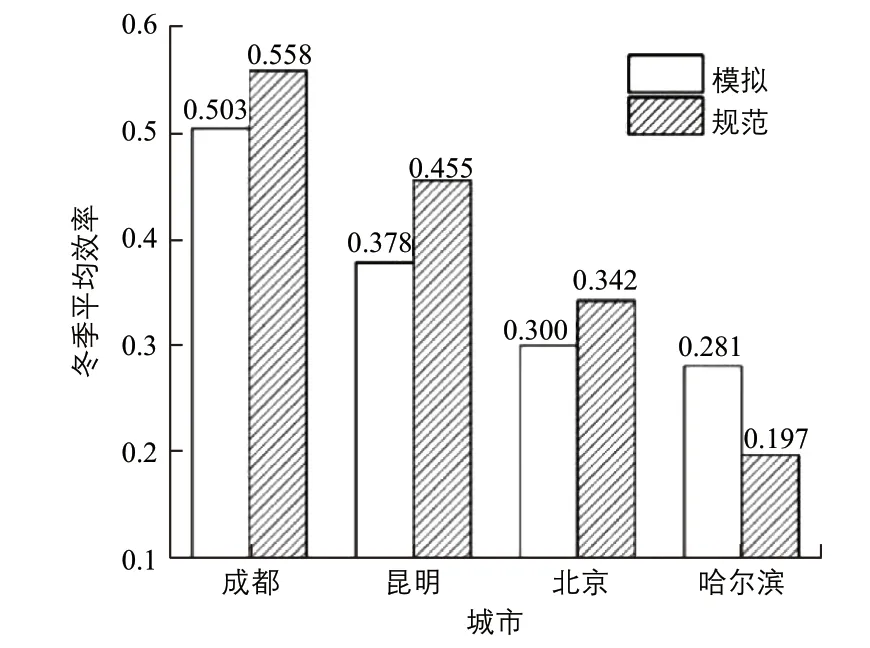
图6 各城市冬季平均效率的模型模拟结果与《规范》计算结果比较图

从图6可以看出，成都、昆明、北京的冬季平均效率的模拟结果均比《规范》计算结果偏低，造成这一差异的原因与上段所述原因大致相同。而在哈尔滨，《规范》计算结果比模拟结果偏小，这是因为《规范》未考虑实际运行中集热器入口温度、流量的变化，其集热器入口温度为某一设定值，哈尔滨冬季气温很低，集热器入口温度随热损失的增大而降低，在其余因素不变的情况下，集热器入口温度越低，集热效率越高，因此在二者耦合作用下，哈尔滨的冬季实际集热器的集热效率并无《规范》计算结果计算的那么低。

当集热效率计算值偏高时，集热器面积设计值则会偏小，在实际运行过程中，会造成个别时候太阳能集热系统所集热量不能满足用户需求的情况。

因此，同是短期蓄热系统，在全年运行和冬季运行的系统中，集热器的集热效率应分开计算取值。《规范》计算虽简单、方便，但为更贴近实际，减少不必要的能源浪费，采用本模型可更精确地模拟实际工程情况，根据实际环境及运行参数，计算某时间段内的集热器平均效率。

4 结论

本文利用一种可结合环境气象数据等参数来计算一段时间内集热效率分布的数学模型，将其置于4个不同气候区的典型城市进行分析，并将该模型与工程常用计算方法进行对比。结果表明，研究集热器的集热效率时，应结合气候进行具体研究，冬季的瞬时效率并非总是低于夏季；在某些年平均气温较低的城市，全年效率分布因集热器入口温度和气象条件的耦合影响呈“W”型；同是短期蓄热系统，全年运行和冬季运行的系统，效率应分开计算取值。

本模型是一种更加适应不同气候地区的集热器热性能模型，可为工程实例中平板太阳能集热器平均效率的选取提供参考。