河流悬移质通量估算方法比较及结果影响因素分析

2019-05-13

人民长江 2019年4期

(武汉大学水资源与水电工程国家重点实验室，湖北武汉 430072)

1 研究背景

对河流物质通量的准确估算，可以掌握河流各种物质输移的时空分布，为河流水环境治理工程提供决策依据。

河流物质瞬时通量是瞬时流量和瞬时浓度的乘积，而时段通量则是由两者乘积关于时间的积分[1-3]。精确计算河流物质时段通量，理论上需要对该河段控制断面的流量和物质浓度做长时间连续观测。而在实际监测工作中，往往无法做到这一点。我国大中型河流水质测站的观测周期一般为15 d或1个月[4-5]。以这些观测资料为基础的不同年通量估算方法的准确性如何一直受到广泛关注[6-9]。

B.W.Webb[10]采用英国河流多年流量和水质观测数据分析了6种时段通量估算方法的表现和适用性。A.Coynel[11]分析了采样频率和采样方法对各时段通量估算方法精度的影响。P.J.Johnes[12]从估算方法、采样频率、流域人口密度等方面分析了磷通量估算的不确定性。国内学者中，富国[13-14]分析比较了5种通量估算方法的差异，并结合长江和黄河的实测数据，对5种方法做了误差分析。郝晨林[15]对5种方法应用于不同污染物时段通量计算时的误差大小进行了分析。

本文试图以观测较密的悬移质泥沙数据为基础，通过用不同时间间隔选取数据，对6种通量估算方法得到的结果进行误差分析，为水质通量的估算提供参考。

2 数据获取及方法

2.1 数据来源

选取1980年长江干流32个水文测站和乌江16个水文测站的逐日流量和逐日含沙量数据，作为本次研究的基本数据[16]。

2.2 基准通量的计算

根据实测每日流量和含沙量数据，基准年通量计算式如式(1)所示[17]。

(1)

式中，Fref表示基准年通量,t/a；Qi为实测日平均流量,m3/s；Ci为实测日平均含沙量,kg/m3；i为时间序列号。由于年通量的准确值较难获取，因此采用准确度较高的基准年通量Fref作为参照值，以评估不同方法估算结果的精度。

2.3 通量估算方法

在物质浓度的实际测量过程中，很难做到连续监测[18-19]。一般的观测周期为15 d或1个月。表1给出了时段通量估算的6种常用方法。

表1 时段通量估算方法[1]Tab.1 Load estimation Methods

注：表中K表示时间转换系数(取决于估算时间段的长短)。

2.4 评价指标

对通量估算方法的评价分为两方面：无偏性和稳定性。

无偏性通过式(2)评估：

(2)

式中，α表示无偏性评价指标，Fmean表示通量计算均值。α表示方法本身的系统误差，α越接近0，则系统误差越小；α>0，则表明估算均值大于真实值；反之，则表明估算均值小于真实值。

稳定性通过式(3)评估：

(3)

式中，β表示稳定性评价指标，δ表示标准差。β反映随机计算结果相对均值的离散程度，表征算法的稳定性。β越小，则算法越稳定；反之，则算法稳定性越差。

2.5 随机模拟次数确定

将6种通量估算方法分别应用到长江流域及乌江流域48个测站，采用7，15，30 d共3种采样周期，分析各方法的适用性。应用Monte Carlo方法[20]对不同采样方案做随机模拟，得到计算均值、标准差等统计学数据。为确定最小随机计算次数，针对不同采样方案做大量模拟计算。计算结果表明，不同采样方案下(7，15，30 d)，当随机模拟次数达到600次以后，均值和标准差均趋于稳定。因此，本次研究针对每个计算方案的随机模拟次数均限定为600次。

3 计算结果分析

3.1 采样频率对通量估算结果的影响

本次研究涵盖长江干流沿程36个测站以及乌江干流沿程12个测站。根据测站的控制流域面积以及空间分布，选取石鼓(21.42万km2)、宜昌(100.55万km2)、大通(170.54万km2)、武隆(8.30万km2)4个典型测站，分析采样频率(周期)对通量估算结果的影响。

图1给出了4个典型测站在应用不同通量估算方法时，α值与采样周期之间的关系。由图1可知，在宜昌站和大通站，采样周期增大对6种估算方法的值几乎没有影响。在石鼓站，当采样周期超过15 d，C、D、E方法计算所得的α值略有微波动，而F方法计算的α值显著增大。在武隆站，当采样周期超过5 d，C、D、E方法α随着采样周期增大而产生波动，且整体呈减小趋势，减小幅度不大；而F方法所得的α值会随着采样周期继续增大，急剧增大。

由图1可知，不考虑采样周期变化对值的影响，不同估算方法自身的值存在差异。在采样周期较小的情况下，A、B方法α普遍小于0，而C、D、E、F方法则十分接近0。这表明，将A、B方法应用到泥沙通量估算时，算法自身存在系统误差，估算值较真实值偏小。在不同的测站，估算值较真实值偏小的百分比有较大差异。例如，大通站的仅为-0.25，而在武隆站值接近-0.50，也即估算值仅为真实值的一半。

图2给出了4个典型测站在应用不同通量估算方法时，β值与采样周期之间的关系。由图2知，A、B、C、D、E方法的β与采样周期之间总体呈正相关关系，且接近线性相关。不同测站β的增长速率存在差异，例如采样周期为30 d时，大通站β取值接近0.12，而宜昌站β取值则接近0.30。

当测站控制流域面积较大时(如大通站和宜昌站)，F方法计算的β值与采样周期接近线性正相关关系。而当测站控制流域面积较小(如石鼓站和武隆站)时，F方法计算的B与采样周期之间的关系较复杂，可分为两段。当采样周期小于某一临界值时，β与采样周期接近线性正相关关系；而当采样周期大于这一临界值时，β急剧增大，且β与采样周期得相关性变弱，F方法基本失效。不同测站的采样周期临界值差异较大，如石鼓站的临界采样周期为21 d，而武隆站则为9 d。

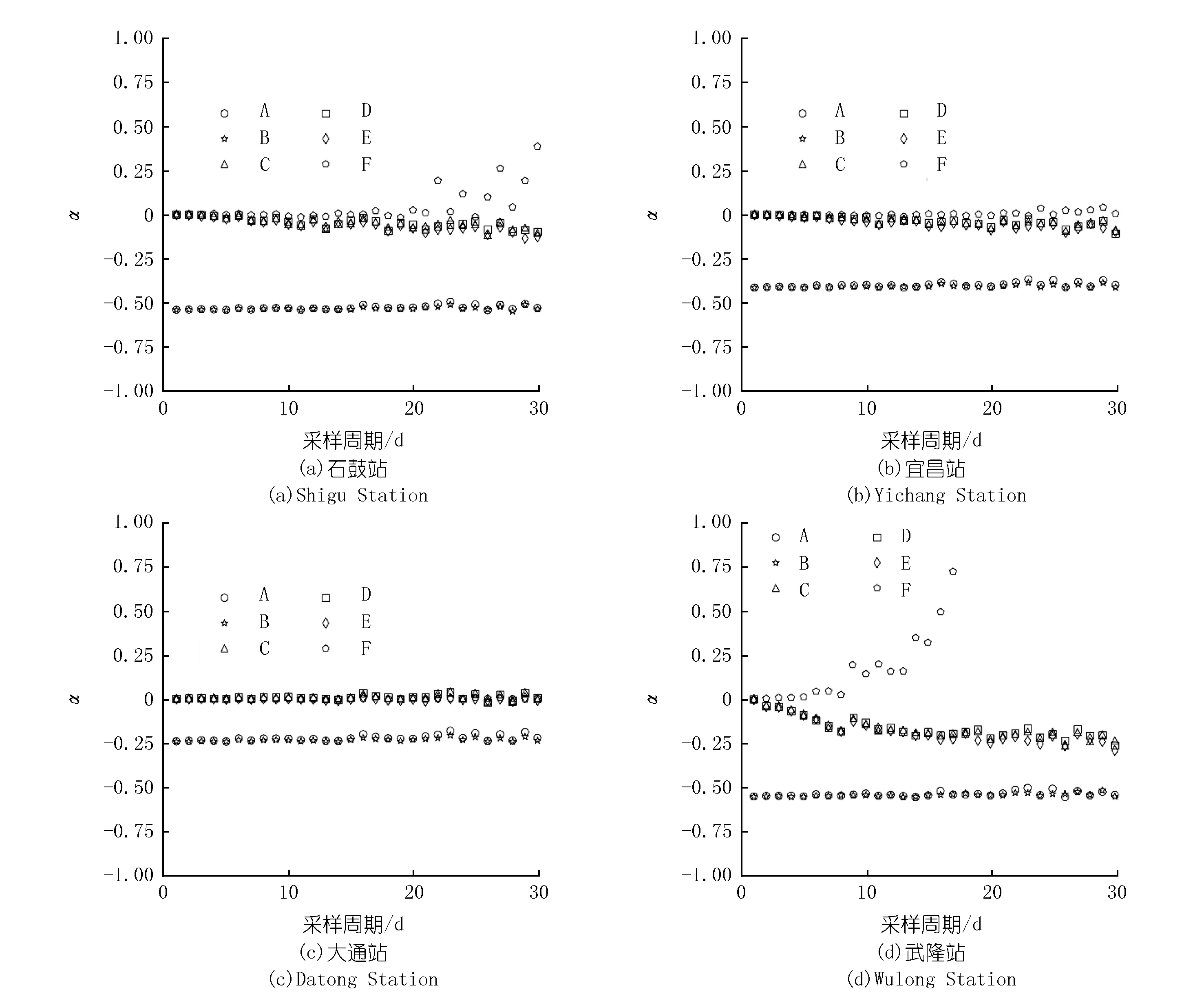
图1 α与采样周期关系Fig.1 Relationship between α and the sampling period

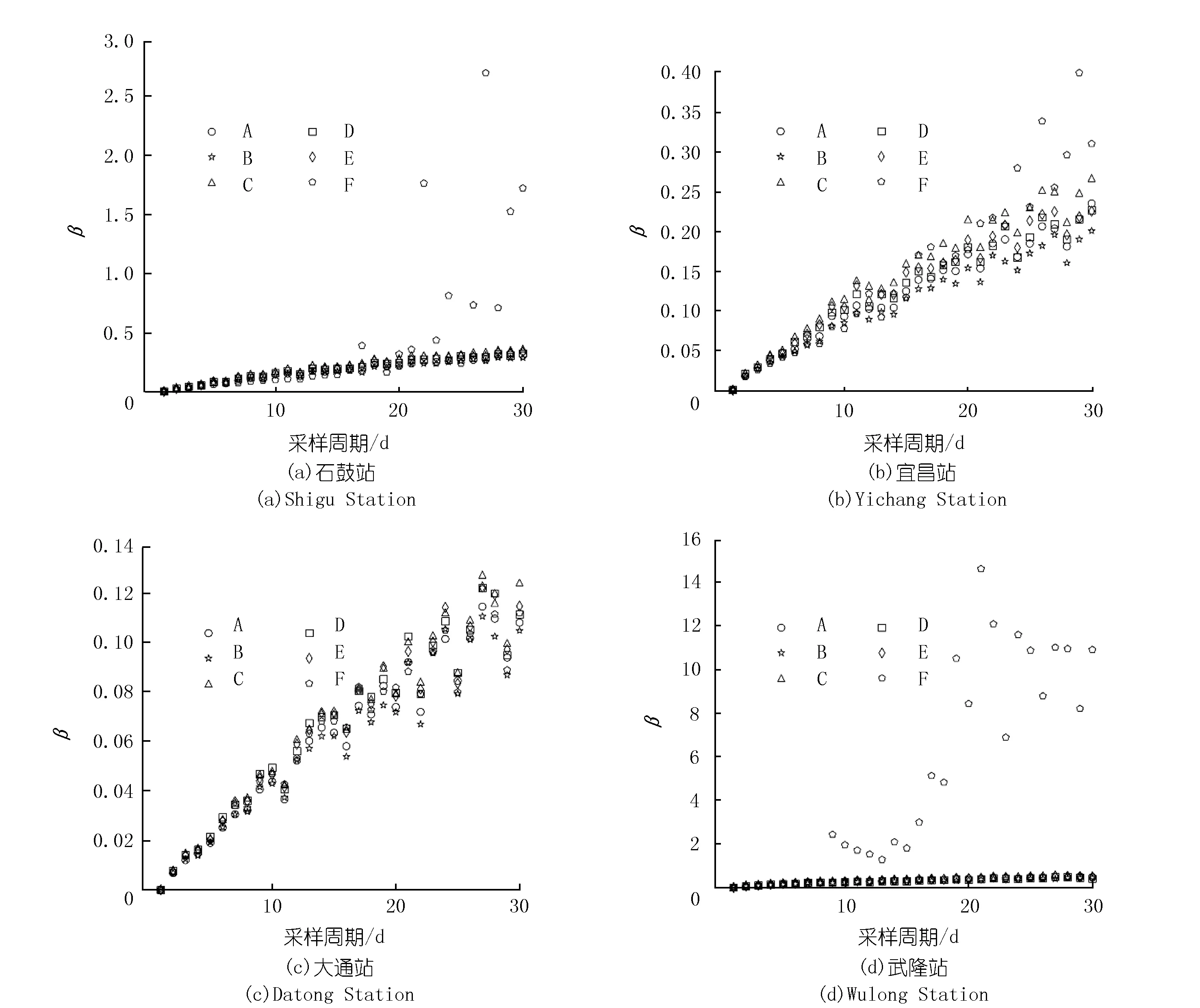
图2 β与采样周期关系Fig.2 Relationship between β and the sampling period

在同一测站，不同估算方法值的大小关系不甚明确。以宜昌站为例，当采样周期为10 d时，βC>βE>βD>βA>βB>βF；而当采样周期为30 d时，βF>βC>βA>βE>βD>βB。βF对采样周期的变化较为敏感，即当采样周期较小时，βF最小，而当采样周期增大到一定程度以后，βF反而最大。

3.2 流域面积对通量估算结果的影响

由前文分析知，几种算法的表现与测站控制流域面积相关。当测站控制流域面积较小时，算法的系统误差会出现不同程度的增大，算法稳定性也会变差。为了进一步分析，选取长江干流沿程以及乌江沿程主要测站作为研究对象，研究测站控制流域面积对通量估算方法的具体影响。选取测站的控制流域面积最小不到0.1万km2(如乌江大溪河鸣玉站)，最大则达到了100万km2(如大通站)以上，基本可反映天然河流通量估算的所有情形。

图3表示6种不同通量估算方法的α与流域面积之间的关系。由图3知，A、B、C、D、E算法所得的α与测站控制流域面积呈正相关关系，而F算法算得的α值则呈现相反的规律。总体而言，计算断面控制流域面积越大，算法系统误差越小。而由α与流域面积的相关性知，当流域面积较小时，A、B、C、D、E方法的通量估算值较基准值偏小，且流域面积越小，偏小程度越大；而F方法的通量估算值较基准值偏大，并且当流域面积极小时，估算值远远大于基准值，算法基本失效。

由图3(f)可知，当计算断面的控制流域面积小于某一临界值(约在1万～10万km2之间)时，α急剧变大，甚至超出图中纵坐标范围，此时估算均值是基准值的数倍，计算结果严重失真。流域面积临界值与数据序列的采样周期也有关系：采样周期越大，这一临界值越大。以上分析表明，F方法并不适用于较小流域的通量估算，尤其当数据序列的时间跨度较大时，其适用范围更窄。

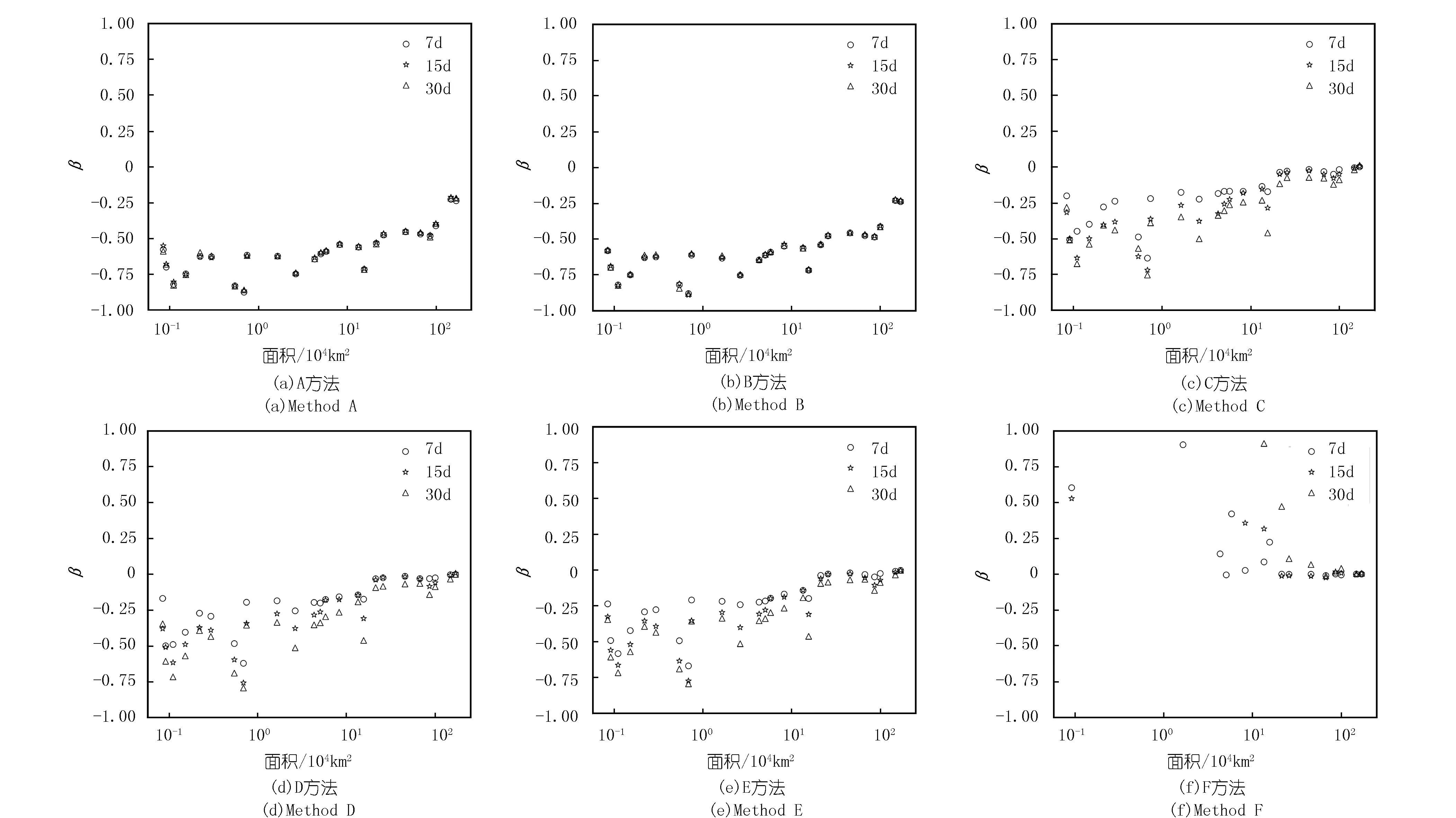
图4 β与流域面积关系Fig.4 Relationship between β and the drainage area

由图4可知，β与流域面积之间呈负相关关系，即测站控制流域面积越大，算法稳定性越好。

由图4(a)～(e)可知，A、B、C、D、E方法规律比较接近，β与流域面积之间呈近似线性关系，且采样周期越大斜率越小。当流域面积较小时，β可能大于1。此时，单次估算值可能是均值的2倍以上，即使算法本身没有系统误差，估算结果也有可能偏离实际值较远。由图4还可知，采样周期较小时，可在一定程度上减小值。因此，在估算控制流域面积较小的断面通量时，应当具备采样频率较高的数据序列，否则，计算结果会出现较大波动，可能与实测值相差数倍。

由图4(f)知，当流域面积较大时，F方法所得规律与A、B、C、D、E方法类似。当流域面积小于某一临界值(约在1万～10万km2之间)时，β远大于1，结果严重失真。此时，通过缩短采样周期并不能显著改善计算结果，F方法完全不适用。

综合以上分析，6种算法的估算结果与测站控制面积之间均存在显著相关关系。测站控制流域面积越大，算法表现越好。而当测站控制流域面积小于临界值时，算法的无偏性和稳定性都会变差，计算结果出现不同程度的失真。