V ariationaland diffusion M onte Carlo simulationsof a hydrogen molecular ion in a sphericalbox*
2019-05-11XuehuiXiao肖学会KuoBao包括YouchunWang王友春HuiXie谢慧DefangDuan段德芳FuboTian田夫波andTianCui崔田
XuehuiXiao(肖学会),Kuo Bao(包括),YouchunWang(王友春),HuiXie(谢慧),Defang Duan(段德芳),Fubo Tian(田夫波),and Tian Cui(崔田)
State Key Laboratory ofSuperhard Materials,College ofPhysics,Jilin University,Changchun 130012,China
(Received 14 January 2019;revisedmanuscript received 26 February 2019;published online4April2019)
Keywords:Monte Carlo simulation,molecule-in-a-boxmodel,high pressure
1.Introduction
In recent years,studies focused on the change in atom ic and molecular system properties during conf inement inside penetrable or impenetrable boundaries.Atoms ormolecules are known to exhibitdifferentelectricaland structuralbehaviorswhen squeezed into asmallspace.Therefore,determ ining how these changesoccur is important.With theemergence of modern nanostructured materials,such as carbon nanotubes,which are ideal containers formolecular insertion and storage,research on conf inedmolecules has become increasingly meaningful.Researchershave recently succeeded in inserting atoms and molecules into fullerene cages and derivatives in experiments.[1]Additionally,conf ined molecules can be applied to the study of high-pressurematerials with molecular hydrogen.[2]The exploratorymodelmustbe supplemented to better understand the basic change mechanism in the electronic and structuralpropertiesof the restrictedmoleculesand atoms.
The hydrogenmolecular ion H+2,with only one electron and two protons,isone of the simplestmolecular ion systems in theuniverse.In recentyears,many researchershavestudied the propertiesof the hydrogenmolecular ion and its isotopes,such as the cold trapped molecular ion[3,4]and the effect of H+2in the interaction ofH2with transitionmetals.[5]Recently,Silva et al.[6]calculated the energy and polarizability of H+2conf ined to an ellipsoidal box in the ground and the f irstexcited states with the variationalmethod.Themolecules are conf ined to an ellipsoidal box to study the properties of the molecules,which canalso be calledmolecule-in-a-boxmodel.Thismodel is simple but effective.The molecule-in-a-box modelwas f irst proposed[7]to calculate the kinetic energy of one hydrogen atom.Over the years,thismodel has been extensively used,especially in smallmolecular systems,such as hydrogen and helium systems.The ground-state energy of the hydrogen molecule and molecular ion in the ellipsoidal box was reported to f ix the protons in the focus position of the box by LeSar and Herschbach[8,9]using a f ive-term James–Coolidge variational function and by Pang[10]using quantum Monte Carlo simulation.Although previous researchers acquired somemeaningful results,[11–13]they ignored the zeropointmotion of protons.Cruz et al.f irst attempted the creation of protonsaway from the specialpointunder thehydrogenmolecular ion system[14]and then applied this change to the system.[15,16]They relaxed the position of protons to allow freemovementon the sem i-majoraxisof the ellipsoid,resulting the change in the equilibrium distance between protons and the total ground-state energy of the hydrogenmolecules corresponding to f ixed size and shape.Assum ing that the protons canmove freely in the ellipsoid instead of only moving on a semi-major axis,we continue tomake improvements to thismodel in thiswork.
Given that the model is a typical quantum atom sys- tem,theoreticalstudy on hydrogen is rather diff icult.The researchersmanaged to develop threemain theoreticalmethods,namely,density functional theory,[17–19]molecular dynam ics simulation,[20,21]andMonteCarlo(MC)simulation.[22–24]For simplicity of treating the dissociation of hydrogen[25]and the zero-pointmotion of protons,we choose MC simulation to study the system in this work.Considering the degrees of freedom of electrons and protons,we extend the previous molecule-in-a-boxmodel,and study the hydrogenmolecular ion in asphericalbox asa three-body problem.Thevariational Monte Carlo(VMC)and diffusion Monte Carlo(DMC)methodsareused to accurately solve the three-body problem under the conf inementcondition,and their calculation precisionsare enough to reach the required accuracy.
Thispaper isorganized in the follow ingmanner.Section 2 providesadetailed theoreticaldescription,including the theoreticalmodel,trialwave function,and Markov Chain.Section 3 shows our resultson the propertiesof the ground state and the comparison of these resultswith previous studies[6,8]to analyze differences in f indings.The last section concludes the paperand presents furtherdiscussion.
2.Theory
2.1.The theoreticalm odel
The original idea of themolecule-in-a-boxmodel is that one can place H+2into an ellipsoidal box,where the protons are f ixed at the focal points of the sem i-major axis,and the electron canmove freely in the ellipsoid.Given that the protonsare f ixed,thismodelsimulates thepropertiesunderdifferent constraint conditionsby changing the volume or shape of the ellipsoidal box,such as the ground-state energy,equilibrium bond length,and kinetic energy of electron.Themodel has been applied to simulate the pressure effect of atoms,molecules,and other bound electron systems.[6,8,10,26–28]Although themolecule-in-a-boxmodelworkswellwhen dealing with variouspropertiesofmatter,itoverestimates theeffectof compression inmost cases.We use a revised version of the molecule-in-a-boxmodel in the presentwork.By using this conf iguration as the starting point,the electron and proton can move freely inside thebox to follow theMarkov chain.
For themolecule-in-a-boxmodel,theboundary isdef ined by
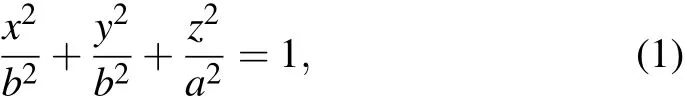
where a and b are the semi-major and sem i-minor axes,respectively.
The Hamiltonian of thissystem can bew ritten as
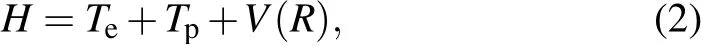
where Te(Tp)represents the kinetic energy of electron(protons)and V(R)is the Coulomb potentialenergy of thissystem,which can bew ritten as

In thispaper,subscript1 represents theonly electron,and subscripts 2 and 3 represent the protons.The previousmoleculein-a-boxmodelcalculation did notconsider themotion of protonsand did nothave the term Tp.Given thatonly two protons and one electron exist in the hydrogenmolecular ion,the potential energy only contains two items,namely,the potential energy between the electron and protons and the potentialenergy between the two protons.Thesetting ofatomicunitsused in thiswork is me=e=¯h=1.
The Schr¨odingerequation can bew ritten as follows:

whereΨisthechosen trialwave function,and E isthegroundstate energy of H+2.In this work,we use VMC and DMC methods to simulate H+2in a spheroidal box as a three-body problem.
2.2.The trialwave function
Thequality of the trialwave function can affect the calculation speed and resultsin VMC and DMC simulations.Therefore,selecting the trialwave function is crucial.The chosen trialwave function in thiswork contains themolecularorbital wave function of electron,themovementof protons,and the boundary conditions.This function isw ritten in the follow ing form:

whereΦ1is the molecularorbitalwave function,which isw ritten as the linear combination of atom ic orbital[10]Φ2denotes the movementof protons[29,30]and isw ritten as


and g(ri)describes the boundary conditions caused by the spheroidalbox[10]as follows:

The wave function satisf ies the zero value when the electron or proton isoutside of the spheroidalbox.In the abovementioned trialwave function,α,C1,and C2are the variational parameters.In the process of VMC simulation,we can f irst optim ize the chosen trialwave function and ground-state energy of H+2to determine the variational parameters.Simultaneously,the sem i-major axisand corresponding sem i-m inor axis are adjusted to determ ine their values at the lowest energy.On the basis of the VMC simulation,we use the DMC method to reconf irm the valuesof sem i-majorand sem i-m inor axes for a given volume and accurately calculate the related physicalquantitiesof thissystem.
2.3.M arkov chain
In the calculation process,we explore themovement of the proton and electron by using theMarkov chain in theMC simulation.Themovementof the proton and electron can be respectivelyw ritten in the follow ing forms:
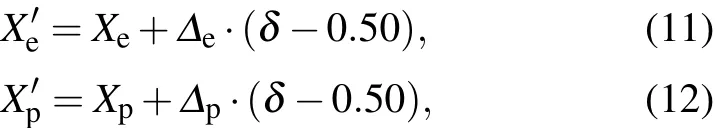
where Xe(X′e)and Xp(X′p)are the vectors in terms of electron and proton positions,respectively;δis a random number between 0 and 1;andΔeandΔprepresent themaximum distancesof electron and protonmovementeach time,respectively.The preceding formula ensures that the electron(proton)random ly moves between-0.5Δe(-0.5Δp)and 0.5Δe(0.5Δp)in theellipsoid.Xeand Xpare thepositionsofelectron and proton at thismoment,respectively,which are subjected to a dynamic rule process(Eqs.(11)and(12))to random ly generate thenextpositions X′eand X′p.Thisphenomenon is the concept of the Markov chain,which is one of the important factorsof stochastic simulation.
3.Results
We calculate the ground-state energy of H+2in different volumes using two MC simulationmethods.Figure 1 shows the relationship between the ground-state energy and the box volume,where the energy increaseswith the decrease in volume.The energy slightly changes with the decrease in volumewhen the volume is larger than 200a30(a0is the Bohr radius).However,the energy rapidly changeswhen the volume is smaller than 200a30mainly due to the increase in pressure and system energy as the volume decreases.Under the same conditions,our resultsare similar to those of LeSarand Silva but slightly larger,mainly becausewe consider themotion of the proton and include itskinetic energy.
Through the change in theground-stateenergy of thissystem along with the bound volume,we can obtain the pressure corresponding to the given volume in accordance with the equation P=-∂E/∂V.Figure 2 provides the equation of states(EOS)of the H+2system.In Fig.2,the calculated pressuresare larger than those of LeSar for the same density.When the density is small,the calculated pressures and those of LeSar are almost the same.However,with the increase in density,our results aremuch higher than their calculated results.Given the lim itation of thismodel,the calculations of this study and those of LeSar are slightly larger than the real values.The largestdifferencebetween ourcalculation and that of others is that the protonsare not f ixed in the special points,such as the focusesof thespheroidalbox.Thus,thezero-point motion of the protonsbecomesevidentunder large density.

Fig.1.The ground-state energy(E)of hydrogen molecular ion versus the volume(V)of the spheroidalbox.Black squaresare our DMC calculation results.Red circles represent LeSar’s results,[8]and green triangles representSilva’s calculation results.[6]The trendsof the three curvesarebasically consistent,butour calculation resultsare larger.
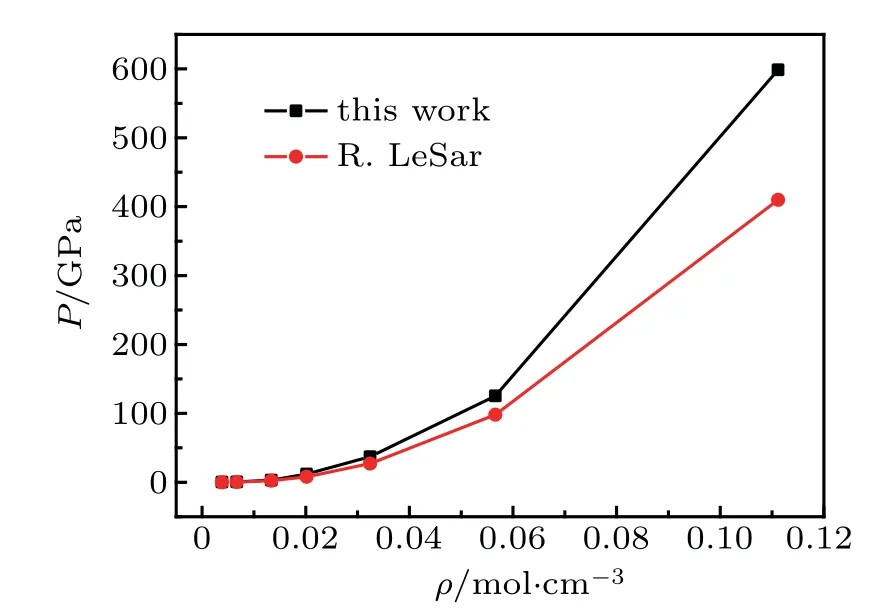
Fig.2.The pressure versus the corresponding density.The black squares are our results,and the red circles are LeSar’s results.[8]At the low density,our resultsarebasically the sameas thoseof LeSar,but as the density increases,our resultsarehigher than LeSar’s results.
Themajor difference between the presentwork and the previous studies is the assumption that the protons and electron canmove freely in thesameway in thesimulation process as emphasized earlier.Therefore,the calculations of the distances between protons under different pressures are crucial.Figure 3 presents the calculation results for themobilemodel and those obtained by the previous f ixed model.In Fig.3,the distances calculated in themobilemodel are larger than those calculated in the f ixedmodel,but the trends of the two curves are the same.The distances between the protons decrease as the pressures increase.On our calculated curve,the distance is observed to have a slight increase ata pressure of approximately 0.4 GPa.This phenomenonmay be related to the reduction in theelectron density in thebox.[16]Notably,the calculated distance in the volume of 879a30is experimentally sim ilar to the bond length of the hydrogenmolecular ion.Our result is 2.09a0,and the experimental result is 2.08a0.This f inding also proves that the chosen trialwave function is reasonableand our calculationsareaccurate.
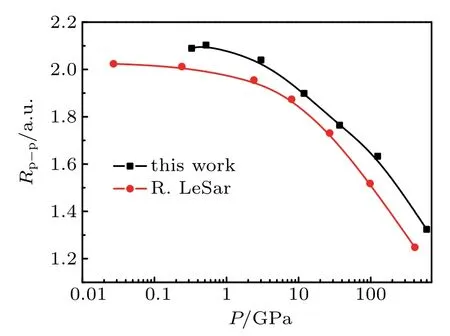
Fig.3.The distance between protons versus the pressure.The black squares are our results in the mobile model,and the red circles are LeSar’s results.[8]
We calculate the averageΔein the VMC simulation to better understand themotion of electron and protons and the effects of considering themotion of protons.Figure 4 shows that the averageΔein themobile model is larger than that in the f ixed model,and the trends of the two curves are the same.The averageΔeincreaseswith the increase of the sem imajoraxis.However,Δein themobilemodelincreases rapidly with the sem i-majoraxisof less than 4.0 a.u.,and the grow th ofΔeis slow ly or even basically unchanged when the semimajor axis exceeds 4.0 a.u.In the f ixed model,the turning point is around 3.0 a.u.,andΔestill increases slow ly when the sem i-major axis is larger than 3.0 a.u.,indicating that the motion of protons can affect themotion of theelectron.Considering themotion of the proton,the change trend ofΔein themobilemodel is obviously different from that in the f ixed model,which is sim ilar to a certain phase transition.However,Δeis justa calculating parameter,which is notdirectly related with measurements.The discontinuousΔedoes not necessarily indicate a traditional phase transition,which generallymeans thatdue to the changes in temperature,pressure,or otherexternal conditions,certain propertiesof themedium usually change discontinuously.In order to observe the impactof protonmotion on electronmotion and verify if there is a phase transition,we calculate the corresponding kinetic energy of theelectron(Te)atdifferentvolumesin the twomodels and the relationship between Teand 1/V.Figure5(a)demonstrates that the kinetic energy decreaseswith the increase in box volume,and Tein themobilemodel is larger than that in the f ixedmodel.We calculate Teunder the twomodels in detail(see Table 1)and f ind that the kinetic energy increasesby about5%.Combining Figs.4 and 5(a)for thesamemodel,the larger the averageΔeis,the smaller the Teis.In Fig.5(b),the variation trends of the curves in the twomodelsare basically the same,and Teand 1/V are basically proportional to each other.We think that there isno obvious phase transition.
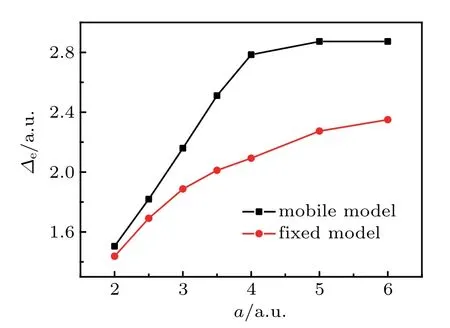
Fig.4.The averageΔe versussemi-majoraxis a(in atomic units).The black squares are the calculation results in themobilemodel,and the red circlesare the calculation results in the f ixedmodel.Themotion of protonmakes theaverage step of theelectronΔe larger.

Fig.5.(a)The average T e versus the volume V and(b)T e versus1/V.Theblack squaresareour resultsin themobilemodel,and the red circles areour results in the f ixedmodel.In panel(a),as the volume increases,the kinetic energy of theelectron T e decreases,and the T e we calculated in themobilemodel is larger than thatcalculated in the f ixedmodel.In panel(b),T e and 1/V in the twomodels are basically proportional to each other.

Table1.The kinetic energy of electron(T e)atdifferentvolumes in the twomodelsand the increase of T e under the corresponding conditions.T(I)e and T(II)e represent the kinetic energy of electron in the f ixed and themobilemodels,respectively.
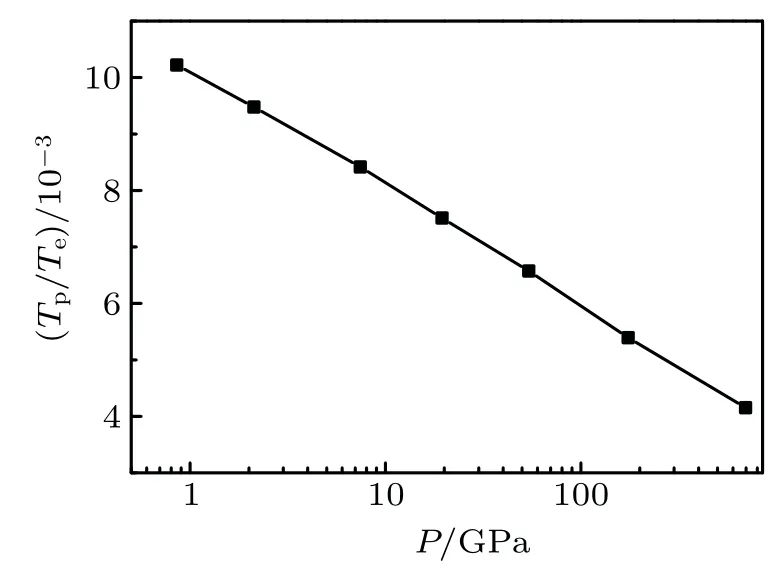
Fig.6.The ratio of average T p and T e versus the pressure.As the pressure increases,T p/T e decreases,indicating that the proportion of T p in the totalkinetic energy decreasesaccordingly.
Finally,we discuss the relationship of the ratio of the kinetic energy of proton and electron(Tp/Te)and pressure.Overall,Tp/Teexponentially decreaseswith increasing pressure.Tp/Teis small and always of the order of a few thousandths in magnitude,which is of the same order ofmagnitudeas the ratio ofmassofelectron and proton.Given that the proton kinetic energy accounts for a small proportion of the totalkinetic energy,thisenergymay be ignored if the calculation accuracy isextremely low,which is related to thespecif ic modeland the discussed problem.This resultprovidesa valuable reference for the calculationmethod,which fails to fully estimate the inf luenceof protonmotion on the possibleerror.
4.Conclusion
In summary,weemploy the improvedmolecule-in-a-box modelwhich is simple buteffective in calculating the groundstatepropertiesof thehydrogenmolecularion underhigh pressure.We consider thezero-pointmotion ofprotonsand regard the hydrogenmolecular ion as a three-body system.Our resultsare larger than the previous results in the f ixedmodeldue to the inf luence of proton motion.In this work,the results show that the totalenergy of the system decreaseswith the increase in volume and the distance between protons decreases with the increase in pressure.Wealso calculate theEOSof the hydrogenmolecular ion,and our resultsaresimilar to thoseof our predecessorsunder low density(low pressure),buthigher than theirs in the high density range.We quantitatively study theeffectof thezero-pointmotionofprotonsonelectrons.The kinetic energy of electrons in themobilemodel increases by 5%compared with that in the f ixedmodel.Finally,the study shows that thekinetic energy of the protons issmallcompared with thatof theelectron,which isonly a few thousandthsof Te.Therefore,Tpcan be neglected when the calculation accuracy is low.
杂志排行
Chinese Physics B的其它文章
- Computational study of inverse ferrite spinels
- Effectsof chem icalpressure on dilutedmagnetic sem iconductor(Ba,K)(Zn,M n)2As2*
- Particle–hole f luctuationsand possible superconductivity in dopedα-RuCl3*
- Surface stabilized cubic phaseof CsPb I3 and CsPbBr3 atroom tem perature*
- Raman scattering study ofmagnetic layered M PS3 crystals(M=M n,Fe,Ni)*
- Low tem perature Pmmm and C2/m phases in Sr2CuO3+δ high temperature superconductor*
